14 . 2 . 1 三角形全等的判定(1)(同步练习)(无答案)2025-2026学年度八年级上册数学人教版(2024)
文档属性
| 名称 | 14 . 2 . 1 三角形全等的判定(1)(同步练习)(无答案)2025-2026学年度八年级上册数学人教版(2024) | 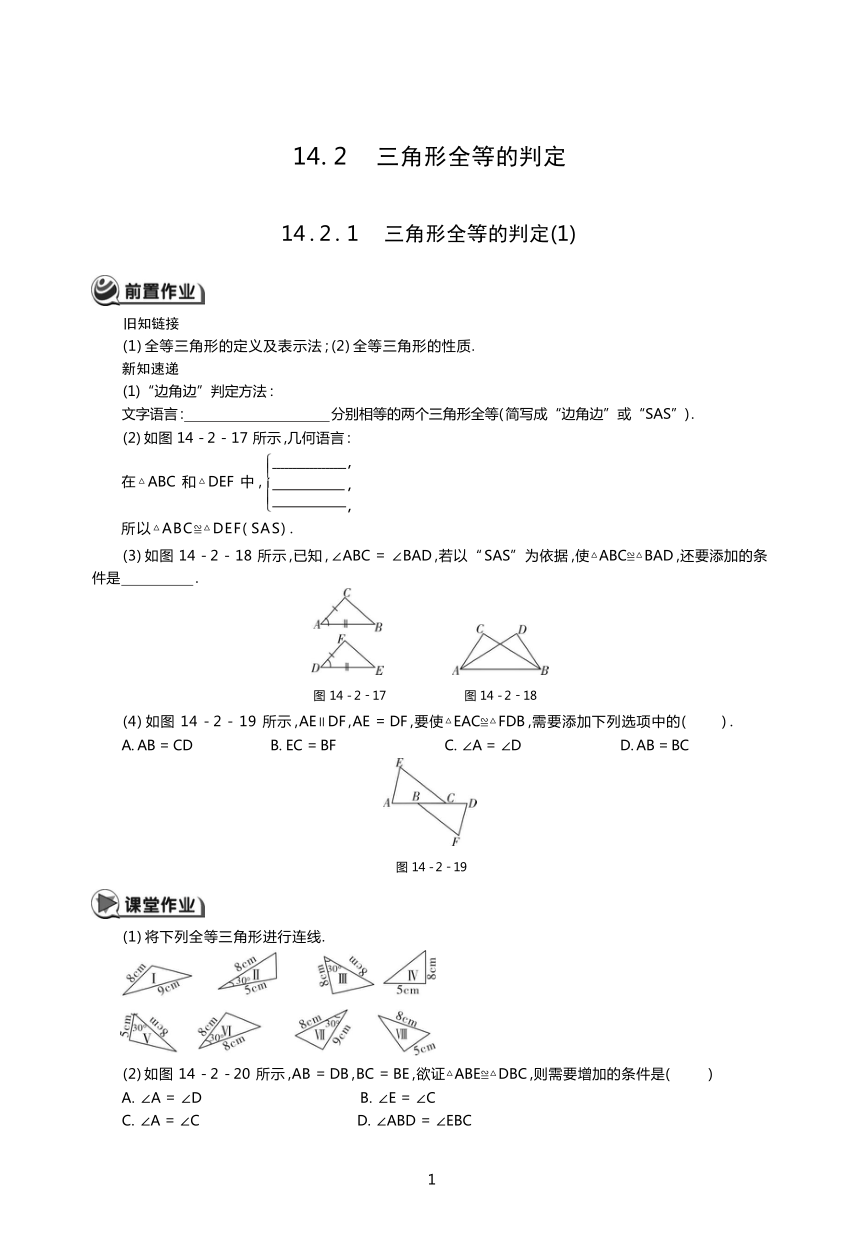 | |
| 格式 | docx | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 07:54:29 | ||
图片预览

文档简介
14. 2 三角形全等的判定
14 . 2 . 1 三角形全等的判定(1)
旧知链接
(1) 全等三角形的定义及表示法 ; (2) 全等三角形的性质.
新知速递
(1)“边角边”判定方法 :
文字语言 : 分别相等的两个三角形全等( 简写成“边角边”或“SAS”) .
(2) 如图 14 - 2 - 17 所示 ,几何语言 :
1
(
)在△ABC 和△DEF 中 , í
,
,
,
所以△ABC≌△DEF( SAS) .
(3) 如图 14 - 2 - 18 所示 ,已知 , ∠ABC = ∠BAD ,若以“ SAS”为依据 ,使△ABC≌△BAD ,还要添加的条 件是 .
图 14 - 2 - 17 图 14 - 2 - 18
(4) 如图 14 - 2 - 19 所示 ,AE∥DF ,AE = DF ,要使△EAC≌△FDB ,需要添加下列选项中的( ) .
A. AB = CD B. EC = BF C. ∠A = ∠D D. AB = BC
图 14 - 2 - 19
(1) 将下列全等三角形进行连线.
(2) 如图 14 - 2 - 20 所示 ,AB = DB ,BC = BE ,欲证△ABE≌△DBC ,则需要增加的条件是( )
A. ∠A = ∠D B. ∠E = ∠C
C. ∠A = ∠C D. ∠ABD = ∠EBC
2
(3) 如图 14 - 2 - 21 所示 ,在△ABF 和△DCE 中 ,点 E、F 在 BC 上 ,AF = DE , ∠AFB = ∠DEC ,添加下列一个条件后能用“SAS”判定△ABF≌△DCE 的是( ) .
A. BE = CF B. ∠B = ∠C C. ∠A = ∠D D. AB = DC
图 14 - 2 - 20
图 14 - 2 - 21
图 14 - 2 - 22
图 14 - 2 - 23
(4) 如图 14 - 2 - 22 所示 ,点 D 在线段 BE 上 ,AB∥CD ,AB = DE ,BD = DC. △ABD 和△EDC 全等吗 为 什么
(5) 如图 14 - 2 - 23 所示 ,点 A、B 分别在 OC、OD 上 ,AD 与 BC 相交于点 E ,OA = OB ,OC = OD , ∠O = 40 ° , ∠D = 20 ° ,求∠AEC 等于多少度.
基础训练
(1) 如图 14 - 2 - 24 所示 ,在△ABD 和△ACE 中 ,AB = AC ,AD = AE. 如果由“ SAS”可以判定△ABD ≌
△ACE ,则需补充条件( ) .
A. ∠EAD = ∠BAC B. ∠B = ∠C
C. ∠D = ∠E D. ∠EAB = ∠CAD
(2) 如图 14 - 2 - 25 所示 ,已知 ,AC 与 BD 相交于点 O ,OA = OD ,OB = OC ,不添加辅助线 ,判定△ABO≌
△DCO 的依据是( ) .
A. SSS B. SAS C. AAS D. ASA
图 14 - 2 - 24 图 14 - 2 - 25 图 14 - 2 - 26 图 14 - 2 - 27
(3) 如图 14 - 2 - 26 所示 ,已知∠AOB ,以点 O 为圆心 ,任意长为半径画弧 ,分别交 OA ,OB 于点 C ,D;再 以点 O 为圆心 ,大于 OC 为半径画弧 ,分别交 OA ,OB 于点 E ,F;连接 CF ,DE ,则△EOD≌△FOC ,其全等的依 据是( ) .
A. SSS B. SAS C. ASA D. AAS
(4) 如图 14 - 2 - 27 所示 ,已知 AC 和 BD 相交于点 O ,若 OA = OD ,用 SAS 证明△AOB≌△DOC 还需添 加的条件是( ) .
A. ∠A = ∠D B. AB = DC
C. OB = OC D. ∠AOB = ∠DOC
拓展提高
(1) 如图 14 - 2 - 28 所示 ,已知∠1 = ∠2 ,如果用 SAS 证明△ABC≌△BAD ,还需要添加的条件是 .
图 14 - 2 - 28 图 14 - 2 - 29 图 14 - 2 - 30 图 14 - 2 - 31
(2) 如图 14 - 2 - 29 所示 ,已知 OA = OB ,OC = OD , ∠O = 50 ° , ∠D = 35 ° ,则∠AEC 等于( ) .
A. 60 ° B. 50 ° C. 45 ° D. 30 °
(3) 如图 14 - 2 - 30 所示 ,已知 AB∥DE ,AB = DE ,BE = CF ,如果∠B = 50 ° , ∠A = 70 ° ,则∠F = ( ) .
A. 70 ° B. 65 ° C. 60 ° D. 55 °
(4) 如图 14 - 2 - 31 所示 ,在 2 × 2 的正方形网格中 , ∠1 + ∠2 等于( ) .
A. 60 ° B. 80 ° C. 90 ° D. 100 °
发散思维
(1) 如图 14 - 2 - 32 所示 ,已知 :在△ABC、△ADE 中 , ∠BAC = ∠DAE = 90 ° ,AB = AC ,AD = AE ,点 C、D、E 三点在同一直线上 ,连接 BD.
①求证 : △BAD≌△CAE.
②请判断 BD、CE 有何大小、位置关系 ,并证明.
3
图 14 - 2 - 32
图 14 - 2 - 33
图 14 - 2 - 34
图 14 - 2 - 35
(2) 如图 14 - 2 - 33 所示 ,点 E 在 AB 上 ,AC = AD , ∠CAB = ∠DAB ,那么△BCE 和△BDE 全等吗 请说 明理由.
(3) 如图 14 - 2 - 34 所示 , △ABC 中 ,AB = 9 ,AC = 6 ,AD 是中线 ,求 AD 得取值范围. ( 提示 :延长 AD 到 E ,使 DE = AD ,连接 BE)
(4) 如图 14 - 2 - 35 所示 ,BD、CE 分别是△ABC 的边 AC 和 AB 上的高 ,点 P 在 BD 的延长线上 ,BP = AC ,点 Q 在 CE 上 ,CQ = AB. 求证 :①AP = AQ ;②AP⊥AQ.
14 . 2 . 1 三角形全等的判定(1)
旧知链接
(1) 全等三角形的定义及表示法 ; (2) 全等三角形的性质.
新知速递
(1)“边角边”判定方法 :
文字语言 : 分别相等的两个三角形全等( 简写成“边角边”或“SAS”) .
(2) 如图 14 - 2 - 17 所示 ,几何语言 :
1
(
)在△ABC 和△DEF 中 , í
,
,
,
所以△ABC≌△DEF( SAS) .
(3) 如图 14 - 2 - 18 所示 ,已知 , ∠ABC = ∠BAD ,若以“ SAS”为依据 ,使△ABC≌△BAD ,还要添加的条 件是 .
图 14 - 2 - 17 图 14 - 2 - 18
(4) 如图 14 - 2 - 19 所示 ,AE∥DF ,AE = DF ,要使△EAC≌△FDB ,需要添加下列选项中的( ) .
A. AB = CD B. EC = BF C. ∠A = ∠D D. AB = BC
图 14 - 2 - 19
(1) 将下列全等三角形进行连线.
(2) 如图 14 - 2 - 20 所示 ,AB = DB ,BC = BE ,欲证△ABE≌△DBC ,则需要增加的条件是( )
A. ∠A = ∠D B. ∠E = ∠C
C. ∠A = ∠C D. ∠ABD = ∠EBC
2
(3) 如图 14 - 2 - 21 所示 ,在△ABF 和△DCE 中 ,点 E、F 在 BC 上 ,AF = DE , ∠AFB = ∠DEC ,添加下列一个条件后能用“SAS”判定△ABF≌△DCE 的是( ) .
A. BE = CF B. ∠B = ∠C C. ∠A = ∠D D. AB = DC
图 14 - 2 - 20
图 14 - 2 - 21
图 14 - 2 - 22
图 14 - 2 - 23
(4) 如图 14 - 2 - 22 所示 ,点 D 在线段 BE 上 ,AB∥CD ,AB = DE ,BD = DC. △ABD 和△EDC 全等吗 为 什么
(5) 如图 14 - 2 - 23 所示 ,点 A、B 分别在 OC、OD 上 ,AD 与 BC 相交于点 E ,OA = OB ,OC = OD , ∠O = 40 ° , ∠D = 20 ° ,求∠AEC 等于多少度.
基础训练
(1) 如图 14 - 2 - 24 所示 ,在△ABD 和△ACE 中 ,AB = AC ,AD = AE. 如果由“ SAS”可以判定△ABD ≌
△ACE ,则需补充条件( ) .
A. ∠EAD = ∠BAC B. ∠B = ∠C
C. ∠D = ∠E D. ∠EAB = ∠CAD
(2) 如图 14 - 2 - 25 所示 ,已知 ,AC 与 BD 相交于点 O ,OA = OD ,OB = OC ,不添加辅助线 ,判定△ABO≌
△DCO 的依据是( ) .
A. SSS B. SAS C. AAS D. ASA
图 14 - 2 - 24 图 14 - 2 - 25 图 14 - 2 - 26 图 14 - 2 - 27
(3) 如图 14 - 2 - 26 所示 ,已知∠AOB ,以点 O 为圆心 ,任意长为半径画弧 ,分别交 OA ,OB 于点 C ,D;再 以点 O 为圆心 ,大于 OC 为半径画弧 ,分别交 OA ,OB 于点 E ,F;连接 CF ,DE ,则△EOD≌△FOC ,其全等的依 据是( ) .
A. SSS B. SAS C. ASA D. AAS
(4) 如图 14 - 2 - 27 所示 ,已知 AC 和 BD 相交于点 O ,若 OA = OD ,用 SAS 证明△AOB≌△DOC 还需添 加的条件是( ) .
A. ∠A = ∠D B. AB = DC
C. OB = OC D. ∠AOB = ∠DOC
拓展提高
(1) 如图 14 - 2 - 28 所示 ,已知∠1 = ∠2 ,如果用 SAS 证明△ABC≌△BAD ,还需要添加的条件是 .
图 14 - 2 - 28 图 14 - 2 - 29 图 14 - 2 - 30 图 14 - 2 - 31
(2) 如图 14 - 2 - 29 所示 ,已知 OA = OB ,OC = OD , ∠O = 50 ° , ∠D = 35 ° ,则∠AEC 等于( ) .
A. 60 ° B. 50 ° C. 45 ° D. 30 °
(3) 如图 14 - 2 - 30 所示 ,已知 AB∥DE ,AB = DE ,BE = CF ,如果∠B = 50 ° , ∠A = 70 ° ,则∠F = ( ) .
A. 70 ° B. 65 ° C. 60 ° D. 55 °
(4) 如图 14 - 2 - 31 所示 ,在 2 × 2 的正方形网格中 , ∠1 + ∠2 等于( ) .
A. 60 ° B. 80 ° C. 90 ° D. 100 °
发散思维
(1) 如图 14 - 2 - 32 所示 ,已知 :在△ABC、△ADE 中 , ∠BAC = ∠DAE = 90 ° ,AB = AC ,AD = AE ,点 C、D、E 三点在同一直线上 ,连接 BD.
①求证 : △BAD≌△CAE.
②请判断 BD、CE 有何大小、位置关系 ,并证明.
3
图 14 - 2 - 32
图 14 - 2 - 33
图 14 - 2 - 34
图 14 - 2 - 35
(2) 如图 14 - 2 - 33 所示 ,点 E 在 AB 上 ,AC = AD , ∠CAB = ∠DAB ,那么△BCE 和△BDE 全等吗 请说 明理由.
(3) 如图 14 - 2 - 34 所示 , △ABC 中 ,AB = 9 ,AC = 6 ,AD 是中线 ,求 AD 得取值范围. ( 提示 :延长 AD 到 E ,使 DE = AD ,连接 BE)
(4) 如图 14 - 2 - 35 所示 ,BD、CE 分别是△ABC 的边 AC 和 AB 上的高 ,点 P 在 BD 的延长线上 ,BP = AC ,点 Q 在 CE 上 ,CQ = AB. 求证 :①AP = AQ ;②AP⊥AQ.
同课章节目录
