2025年秋期九年级上册沪科版数学全册检测题(含答案)
文档属性
| 名称 | 2025年秋期九年级上册沪科版数学全册检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 21:20:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年秋期九年级上册沪科版数学全册检测题
一、单选题(共10题;共30分)
1.(3分)(2024九下·湖南模拟)如图,用一个卡尺( ,)测量气缸的内孔直径,量得的长为,则内孔直径的长为( )
A. B. C. D.
2.(3分)(2024九上·温州开学考)已知点,,在函数的图象上,则( )
A. B. C. D.
3.(3分)(2024·昆明模拟)如图,在中,D,E分别为,上的点.若,,的面积为2,则的面积为( )
A.8 B.16 C.32 D.64
4.(3分)(2024九上·苏州期中)身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同 学 甲 乙 丙
放出风筝线长
线与地面夹角
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
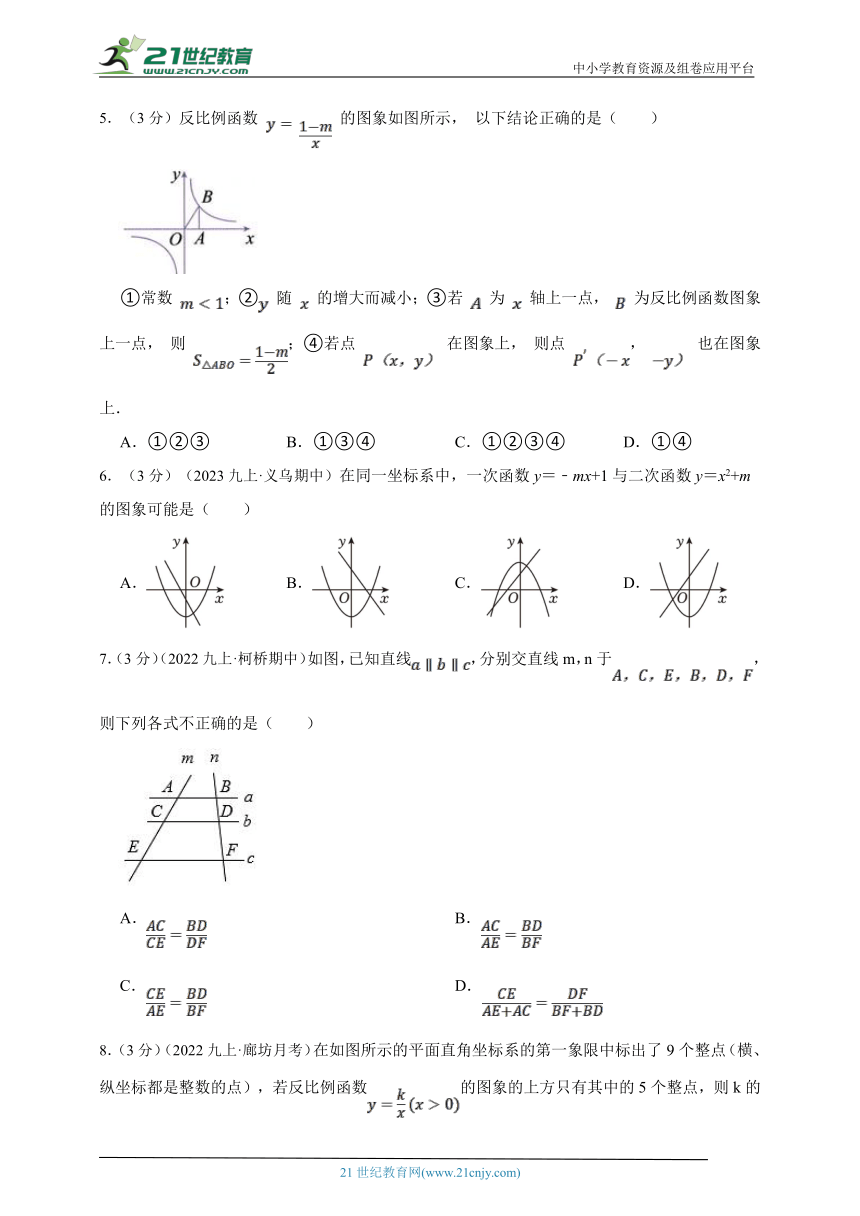
5.(3分)反比例函数 的图象如图所示, 以下结论正确的是( )
①常数 ;② 随 的增大而减小;③若 为 轴上一点, 为反比例函数图象上一点, 则 ;④若点 在图象上, 则点 , 也在图象上.
A.①②③ B.①③④ C.①②③④ D.①④
6.(3分)(2023九上·义乌期中)在同一坐标系中,一次函数y=﹣mx+1与二次函数y=x2+m的图象可能是( )
A. B. C. D.
7.(3分)(2022九上·柯桥期中)如图,已知直线,分别交直线m,n于,则下列各式不正确的是( )
A. B.
C. D.
8.(3分)(2022九上·廊坊月考)在如图所示的平面直角坐标系的第一象限中标出了9个整点(横、纵坐标都是整数的点),若反比例函数的图象的上方只有其中的5个整点,则k的取值范围是( )
A. B. C. D.
9.(3分)(2023八下·桐柏月考)如图,反比例函数)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为6,则k的值为( )
A.-12 B.12 C.6 D.-6
10.(3分)(2024九上·杭州期中)如图,在中,平分,按如下步骤作图:分别以点B,D为圆心,以大于的长为半径在两侧作弧,分别交于两点M,N;作直线分别与,交于点E,F,交于点O,连按,.根据以上作图,一定可以推得的结论是( )
A.是的中位线 B.点O为的重心
C. D.
二、填空题(共6题;共24分)
11.(4分)(2024九上·通州期中)如果,那么的值是 .
12.(4分)
13.(4分)(2025八下·龙湾期中)冬季降水减少,很多河里河水枯竭,正是疏浚河道的好时机.如图是某河堤的横断面,堤高米,迎水坡的坡比是,则河堤的长是 米.
14.(4分)(2023九上·东乡区期中)已知,则 .
15.(4分)(2024九上·云梦月考)已知:如图,在平面直角坐标系中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则正方形的边长A B的最小值是 .
16.(4分)(2024八下·靖江月考)如图,已知在长方形纸条中,点G在边上,,将该纸条沿着过点G的直线翻折后,点C、D分别落在边下方的点E、F处,且点E、F、B在同一条直线上,折痕与边交于点H,与交于点M.设,那么的周长为 (用含t的代数式表示)
三、计算题(共3题;共25分)
17.(5分)(2023九下·袁州模拟)(1)计算:
(2)解不等式组:
18.(5分)(2024九下·湖北模拟)小敏利用无人机测量某座山的垂直高度.如图所示,无人机在地面上方130米的D处测得山顶A的仰角为,测得山脚C的俯角为,已知的坡度为1∶0.75,点A,B,C,D在同一平面内,请帮小敏计算此山的垂直高度(结果精确到0.1米).(参考数据:,,,)
19.(15分)(2024九上·宁波月考)已知二次函数,(p为实数)
(1)(5分)若函数与x轴交于不同的两点,,,求实数p的取值范围.
(2)(5分)若,,是方程的两根,当函数的图像分别与直线相交于A,B两点,与直线相交于C,D两点,当时,求p的值.
(3)(5分)若关于x方程有4个不相等的实数根,求p的取值范围.
四、解答题(共4题;共41分)
20.(14分)(2025九上·淮南期末)已知抛物线与x轴的一个交点为,与y轴的交点为.
(1)(7分)求抛物线的解析式;
(2)(7分)求y的最值.
21.(13分)(2024八下·浦东期中)已知一次函数平行于直线,且与函数有一个交点,求:
(1)(7分)一次函数的解析式.
(2)(6分)此一次函数与两坐标轴围成的三角形面积.
22.(7分)(2023九上·澧县月考)今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且,,靠背,支架,扶手的一部分.这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:,,)
23.(7分)(2023·兴宁模拟)在平面直角坐标系xOy中,抛物线y=a(x﹣3)(x+1)与x轴交于A、B两点,与y轴交于点C(0,),连接AC、BC.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点E为第二象限抛物线上的一动点,EF∥BC,直线EF与抛物线交于点F,设直线EF的表达式为y=kx+b.
①如图①,直线y=kx+b与抛物线对称轴交于点G,若△DGF∽△BDC,求k、b的值;
②如图②,直线y=kx+b与y轴交于点M,与直线y=x交于点H,若﹣=,求b的值.
答案解析部分
1.【答案】D
【知识点】相似三角形的应用
2.【答案】A
【知识点】反比例函数的性质
3.【答案】C
【知识点】相似三角形的判定与性质
4.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】D
【知识点】反比例函数图象的对称性;反比例函数的性质
6.【答案】D
【知识点】二次函数图象与系数的关系;一次函数图象、性质与系数的关系
7.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
8.【答案】A
【知识点】反比例函数的性质;待定系数法求反比例函数解析式
9.【答案】A
【知识点】反比例函数的图象;三角形的面积
10.【答案】D
【知识点】线段垂直平分线的性质;相似三角形的判定
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】勾股定理;解直角三角形的实际应用﹣坡度坡角问题
14.【答案】
【知识点】比例的性质
15.【答案】
【知识点】正方形的性质;二次函数-动态几何问题
16.【答案】
【知识点】等边三角形的判定与性质;矩形的性质;解直角三角形
17.【答案】(1)4;(2)
【知识点】零指数幂;负整数指数幂;解一元一次不等式组;求特殊角的三角函数值
18.【答案】米
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)
(2)
(3)或
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
20.【答案】(1)
(2)
【知识点】二次函数的最值;待定系数法求二次函数解析式
21.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系;反比例函数与一次函数的交点问题
22.【答案】解:方法一:
过点作交的延长线于点,
四边形是平行四边形,,
,
,
过点作于点,
由题意知,,
,
又,
,
过作于点,
,,
,
,
靠背顶端点距地面高度为
;
方法二:
如图,过点作交的延长线于点,过点作于点,延长交于点,
,,
,
又,
,
,
,
过作于,
由题意知,,
,
又,
,
靠背顶端点距地面高度为.
【知识点】平行线的性质;平行四边形的性质;解直角三角形的其他实际应用
23.【答案】(1)y=x2﹣x﹣;(2)①k=,b=;②2
【知识点】一元二次方程的根与系数的关系(韦达定理);待定系数法求二次函数解析式;相似三角形的判定与性质;解直角三角形
2025年秋期九年级上册沪科版数学全册检测题
一、单选题(共10题;共30分)
1.(3分)(2024九下·湖南模拟)如图,用一个卡尺( ,)测量气缸的内孔直径,量得的长为,则内孔直径的长为( )
A. B. C. D.
2.(3分)(2024九上·温州开学考)已知点,,在函数的图象上,则( )
A. B. C. D.
3.(3分)(2024·昆明模拟)如图,在中,D,E分别为,上的点.若,,的面积为2,则的面积为( )
A.8 B.16 C.32 D.64
4.(3分)(2024九上·苏州期中)身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同 学 甲 乙 丙
放出风筝线长
线与地面夹角
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
5.(3分)反比例函数 的图象如图所示, 以下结论正确的是( )
①常数 ;② 随 的增大而减小;③若 为 轴上一点, 为反比例函数图象上一点, 则 ;④若点 在图象上, 则点 , 也在图象上.
A.①②③ B.①③④ C.①②③④ D.①④
6.(3分)(2023九上·义乌期中)在同一坐标系中,一次函数y=﹣mx+1与二次函数y=x2+m的图象可能是( )
A. B. C. D.
7.(3分)(2022九上·柯桥期中)如图,已知直线,分别交直线m,n于,则下列各式不正确的是( )
A. B.
C. D.
8.(3分)(2022九上·廊坊月考)在如图所示的平面直角坐标系的第一象限中标出了9个整点(横、纵坐标都是整数的点),若反比例函数的图象的上方只有其中的5个整点,则k的取值范围是( )
A. B. C. D.
9.(3分)(2023八下·桐柏月考)如图,反比例函数)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为6,则k的值为( )
A.-12 B.12 C.6 D.-6
10.(3分)(2024九上·杭州期中)如图,在中,平分,按如下步骤作图:分别以点B,D为圆心,以大于的长为半径在两侧作弧,分别交于两点M,N;作直线分别与,交于点E,F,交于点O,连按,.根据以上作图,一定可以推得的结论是( )
A.是的中位线 B.点O为的重心
C. D.
二、填空题(共6题;共24分)
11.(4分)(2024九上·通州期中)如果,那么的值是 .
12.(4分)
13.(4分)(2025八下·龙湾期中)冬季降水减少,很多河里河水枯竭,正是疏浚河道的好时机.如图是某河堤的横断面,堤高米,迎水坡的坡比是,则河堤的长是 米.
14.(4分)(2023九上·东乡区期中)已知,则 .
15.(4分)(2024九上·云梦月考)已知:如图,在平面直角坐标系中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则正方形的边长A B的最小值是 .
16.(4分)(2024八下·靖江月考)如图,已知在长方形纸条中,点G在边上,,将该纸条沿着过点G的直线翻折后,点C、D分别落在边下方的点E、F处,且点E、F、B在同一条直线上,折痕与边交于点H,与交于点M.设,那么的周长为 (用含t的代数式表示)
三、计算题(共3题;共25分)
17.(5分)(2023九下·袁州模拟)(1)计算:
(2)解不等式组:
18.(5分)(2024九下·湖北模拟)小敏利用无人机测量某座山的垂直高度.如图所示,无人机在地面上方130米的D处测得山顶A的仰角为,测得山脚C的俯角为,已知的坡度为1∶0.75,点A,B,C,D在同一平面内,请帮小敏计算此山的垂直高度(结果精确到0.1米).(参考数据:,,,)
19.(15分)(2024九上·宁波月考)已知二次函数,(p为实数)
(1)(5分)若函数与x轴交于不同的两点,,,求实数p的取值范围.
(2)(5分)若,,是方程的两根,当函数的图像分别与直线相交于A,B两点,与直线相交于C,D两点,当时,求p的值.
(3)(5分)若关于x方程有4个不相等的实数根,求p的取值范围.
四、解答题(共4题;共41分)
20.(14分)(2025九上·淮南期末)已知抛物线与x轴的一个交点为,与y轴的交点为.
(1)(7分)求抛物线的解析式;
(2)(7分)求y的最值.
21.(13分)(2024八下·浦东期中)已知一次函数平行于直线,且与函数有一个交点,求:
(1)(7分)一次函数的解析式.
(2)(6分)此一次函数与两坐标轴围成的三角形面积.
22.(7分)(2023九上·澧县月考)今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且,,靠背,支架,扶手的一部分.这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:,,)
23.(7分)(2023·兴宁模拟)在平面直角坐标系xOy中,抛物线y=a(x﹣3)(x+1)与x轴交于A、B两点,与y轴交于点C(0,),连接AC、BC.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点E为第二象限抛物线上的一动点,EF∥BC,直线EF与抛物线交于点F,设直线EF的表达式为y=kx+b.
①如图①,直线y=kx+b与抛物线对称轴交于点G,若△DGF∽△BDC,求k、b的值;
②如图②,直线y=kx+b与y轴交于点M,与直线y=x交于点H,若﹣=,求b的值.
答案解析部分
1.【答案】D
【知识点】相似三角形的应用
2.【答案】A
【知识点】反比例函数的性质
3.【答案】C
【知识点】相似三角形的判定与性质
4.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】D
【知识点】反比例函数图象的对称性;反比例函数的性质
6.【答案】D
【知识点】二次函数图象与系数的关系;一次函数图象、性质与系数的关系
7.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
8.【答案】A
【知识点】反比例函数的性质;待定系数法求反比例函数解析式
9.【答案】A
【知识点】反比例函数的图象;三角形的面积
10.【答案】D
【知识点】线段垂直平分线的性质;相似三角形的判定
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】勾股定理;解直角三角形的实际应用﹣坡度坡角问题
14.【答案】
【知识点】比例的性质
15.【答案】
【知识点】正方形的性质;二次函数-动态几何问题
16.【答案】
【知识点】等边三角形的判定与性质;矩形的性质;解直角三角形
17.【答案】(1)4;(2)
【知识点】零指数幂;负整数指数幂;解一元一次不等式组;求特殊角的三角函数值
18.【答案】米
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)
(2)
(3)或
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
20.【答案】(1)
(2)
【知识点】二次函数的最值;待定系数法求二次函数解析式
21.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系;反比例函数与一次函数的交点问题
22.【答案】解:方法一:
过点作交的延长线于点,
四边形是平行四边形,,
,
,
过点作于点,
由题意知,,
,
又,
,
过作于点,
,,
,
,
靠背顶端点距地面高度为
;
方法二:
如图,过点作交的延长线于点,过点作于点,延长交于点,
,,
,
又,
,
,
,
过作于,
由题意知,,
,
又,
,
靠背顶端点距地面高度为.
【知识点】平行线的性质;平行四边形的性质;解直角三角形的其他实际应用
23.【答案】(1)y=x2﹣x﹣;(2)①k=,b=;②2
【知识点】一元二次方程的根与系数的关系(韦达定理);待定系数法求二次函数解析式;相似三角形的判定与性质;解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年秋期九年级上册沪科版数学全册检测题
一、单选题(共10题;共30分)
1.(3分)(2024九下·湖南模拟)如图,用一个卡尺( ,)测量气缸的内孔直径,量得的长为,则内孔直径的长为( )
A. B. C. D.
2.(3分)(2024九上·温州开学考)已知点,,在函数的图象上,则( )
A. B. C. D.
3.(3分)(2024·昆明模拟)如图,在中,D,E分别为,上的点.若,,的面积为2,则的面积为( )
A.8 B.16 C.32 D.64
4.(3分)(2024九上·苏州期中)身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同 学 甲 乙 丙
放出风筝线长
线与地面夹角
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
5.(3分)反比例函数 的图象如图所示, 以下结论正确的是( )
①常数 ;② 随 的增大而减小;③若 为 轴上一点, 为反比例函数图象上一点, 则 ;④若点 在图象上, 则点 , 也在图象上.
A.①②③ B.①③④ C.①②③④ D.①④
6.(3分)(2023九上·义乌期中)在同一坐标系中,一次函数y=﹣mx+1与二次函数y=x2+m的图象可能是( )
A. B. C. D.
7.(3分)(2022九上·柯桥期中)如图,已知直线,分别交直线m,n于,则下列各式不正确的是( )
A. B.
C. D.
8.(3分)(2022九上·廊坊月考)在如图所示的平面直角坐标系的第一象限中标出了9个整点(横、纵坐标都是整数的点),若反比例函数的图象的上方只有其中的5个整点,则k的取值范围是( )
A. B. C. D.
9.(3分)(2023八下·桐柏月考)如图,反比例函数)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为6,则k的值为( )
A.-12 B.12 C.6 D.-6
10.(3分)(2024九上·杭州期中)如图,在中,平分,按如下步骤作图:分别以点B,D为圆心,以大于的长为半径在两侧作弧,分别交于两点M,N;作直线分别与,交于点E,F,交于点O,连按,.根据以上作图,一定可以推得的结论是( )
A.是的中位线 B.点O为的重心
C. D.
二、填空题(共6题;共24分)
11.(4分)(2024九上·通州期中)如果,那么的值是 .
12.(4分)
13.(4分)(2025八下·龙湾期中)冬季降水减少,很多河里河水枯竭,正是疏浚河道的好时机.如图是某河堤的横断面,堤高米,迎水坡的坡比是,则河堤的长是 米.
14.(4分)(2023九上·东乡区期中)已知,则 .
15.(4分)(2024九上·云梦月考)已知:如图,在平面直角坐标系中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则正方形的边长A B的最小值是 .
16.(4分)(2024八下·靖江月考)如图,已知在长方形纸条中,点G在边上,,将该纸条沿着过点G的直线翻折后,点C、D分别落在边下方的点E、F处,且点E、F、B在同一条直线上,折痕与边交于点H,与交于点M.设,那么的周长为 (用含t的代数式表示)
三、计算题(共3题;共25分)
17.(5分)(2023九下·袁州模拟)(1)计算:
(2)解不等式组:
18.(5分)(2024九下·湖北模拟)小敏利用无人机测量某座山的垂直高度.如图所示,无人机在地面上方130米的D处测得山顶A的仰角为,测得山脚C的俯角为,已知的坡度为1∶0.75,点A,B,C,D在同一平面内,请帮小敏计算此山的垂直高度(结果精确到0.1米).(参考数据:,,,)
19.(15分)(2024九上·宁波月考)已知二次函数,(p为实数)
(1)(5分)若函数与x轴交于不同的两点,,,求实数p的取值范围.
(2)(5分)若,,是方程的两根,当函数的图像分别与直线相交于A,B两点,与直线相交于C,D两点,当时,求p的值.
(3)(5分)若关于x方程有4个不相等的实数根,求p的取值范围.
四、解答题(共4题;共41分)
20.(14分)(2025九上·淮南期末)已知抛物线与x轴的一个交点为,与y轴的交点为.
(1)(7分)求抛物线的解析式;
(2)(7分)求y的最值.
21.(13分)(2024八下·浦东期中)已知一次函数平行于直线,且与函数有一个交点,求:
(1)(7分)一次函数的解析式.
(2)(6分)此一次函数与两坐标轴围成的三角形面积.
22.(7分)(2023九上·澧县月考)今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且,,靠背,支架,扶手的一部分.这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:,,)
23.(7分)(2023·兴宁模拟)在平面直角坐标系xOy中,抛物线y=a(x﹣3)(x+1)与x轴交于A、B两点,与y轴交于点C(0,),连接AC、BC.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点E为第二象限抛物线上的一动点,EF∥BC,直线EF与抛物线交于点F,设直线EF的表达式为y=kx+b.
①如图①,直线y=kx+b与抛物线对称轴交于点G,若△DGF∽△BDC,求k、b的值;
②如图②,直线y=kx+b与y轴交于点M,与直线y=x交于点H,若﹣=,求b的值.
答案解析部分
1.【答案】D
【知识点】相似三角形的应用
2.【答案】A
【知识点】反比例函数的性质
3.【答案】C
【知识点】相似三角形的判定与性质
4.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】D
【知识点】反比例函数图象的对称性;反比例函数的性质
6.【答案】D
【知识点】二次函数图象与系数的关系;一次函数图象、性质与系数的关系
7.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
8.【答案】A
【知识点】反比例函数的性质;待定系数法求反比例函数解析式
9.【答案】A
【知识点】反比例函数的图象;三角形的面积
10.【答案】D
【知识点】线段垂直平分线的性质;相似三角形的判定
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】勾股定理;解直角三角形的实际应用﹣坡度坡角问题
14.【答案】
【知识点】比例的性质
15.【答案】
【知识点】正方形的性质;二次函数-动态几何问题
16.【答案】
【知识点】等边三角形的判定与性质;矩形的性质;解直角三角形
17.【答案】(1)4;(2)
【知识点】零指数幂;负整数指数幂;解一元一次不等式组;求特殊角的三角函数值
18.【答案】米
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)
(2)
(3)或
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
20.【答案】(1)
(2)
【知识点】二次函数的最值;待定系数法求二次函数解析式
21.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系;反比例函数与一次函数的交点问题
22.【答案】解:方法一:
过点作交的延长线于点,
四边形是平行四边形,,
,
,
过点作于点,
由题意知,,
,
又,
,
过作于点,
,,
,
,
靠背顶端点距地面高度为
;
方法二:
如图,过点作交的延长线于点,过点作于点,延长交于点,
,,
,
又,
,
,
,
过作于,
由题意知,,
,
又,
,
靠背顶端点距地面高度为.
【知识点】平行线的性质;平行四边形的性质;解直角三角形的其他实际应用
23.【答案】(1)y=x2﹣x﹣;(2)①k=,b=;②2
【知识点】一元二次方程的根与系数的关系(韦达定理);待定系数法求二次函数解析式;相似三角形的判定与性质;解直角三角形
2025年秋期九年级上册沪科版数学全册检测题
一、单选题(共10题;共30分)
1.(3分)(2024九下·湖南模拟)如图,用一个卡尺( ,)测量气缸的内孔直径,量得的长为,则内孔直径的长为( )
A. B. C. D.
2.(3分)(2024九上·温州开学考)已知点,,在函数的图象上,则( )
A. B. C. D.
3.(3分)(2024·昆明模拟)如图,在中,D,E分别为,上的点.若,,的面积为2,则的面积为( )
A.8 B.16 C.32 D.64
4.(3分)(2024九上·苏州期中)身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同 学 甲 乙 丙
放出风筝线长
线与地面夹角
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
5.(3分)反比例函数 的图象如图所示, 以下结论正确的是( )
①常数 ;② 随 的增大而减小;③若 为 轴上一点, 为反比例函数图象上一点, 则 ;④若点 在图象上, 则点 , 也在图象上.
A.①②③ B.①③④ C.①②③④ D.①④
6.(3分)(2023九上·义乌期中)在同一坐标系中,一次函数y=﹣mx+1与二次函数y=x2+m的图象可能是( )
A. B. C. D.
7.(3分)(2022九上·柯桥期中)如图,已知直线,分别交直线m,n于,则下列各式不正确的是( )
A. B.
C. D.
8.(3分)(2022九上·廊坊月考)在如图所示的平面直角坐标系的第一象限中标出了9个整点(横、纵坐标都是整数的点),若反比例函数的图象的上方只有其中的5个整点,则k的取值范围是( )
A. B. C. D.
9.(3分)(2023八下·桐柏月考)如图,反比例函数)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,△PAB的面积为6,则k的值为( )
A.-12 B.12 C.6 D.-6
10.(3分)(2024九上·杭州期中)如图,在中,平分,按如下步骤作图:分别以点B,D为圆心,以大于的长为半径在两侧作弧,分别交于两点M,N;作直线分别与,交于点E,F,交于点O,连按,.根据以上作图,一定可以推得的结论是( )
A.是的中位线 B.点O为的重心
C. D.
二、填空题(共6题;共24分)
11.(4分)(2024九上·通州期中)如果,那么的值是 .
12.(4分)
13.(4分)(2025八下·龙湾期中)冬季降水减少,很多河里河水枯竭,正是疏浚河道的好时机.如图是某河堤的横断面,堤高米,迎水坡的坡比是,则河堤的长是 米.
14.(4分)(2023九上·东乡区期中)已知,则 .
15.(4分)(2024九上·云梦月考)已知:如图,在平面直角坐标系中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则正方形的边长A B的最小值是 .
16.(4分)(2024八下·靖江月考)如图,已知在长方形纸条中,点G在边上,,将该纸条沿着过点G的直线翻折后,点C、D分别落在边下方的点E、F处,且点E、F、B在同一条直线上,折痕与边交于点H,与交于点M.设,那么的周长为 (用含t的代数式表示)
三、计算题(共3题;共25分)
17.(5分)(2023九下·袁州模拟)(1)计算:
(2)解不等式组:
18.(5分)(2024九下·湖北模拟)小敏利用无人机测量某座山的垂直高度.如图所示,无人机在地面上方130米的D处测得山顶A的仰角为,测得山脚C的俯角为,已知的坡度为1∶0.75,点A,B,C,D在同一平面内,请帮小敏计算此山的垂直高度(结果精确到0.1米).(参考数据:,,,)
19.(15分)(2024九上·宁波月考)已知二次函数,(p为实数)
(1)(5分)若函数与x轴交于不同的两点,,,求实数p的取值范围.
(2)(5分)若,,是方程的两根,当函数的图像分别与直线相交于A,B两点,与直线相交于C,D两点,当时,求p的值.
(3)(5分)若关于x方程有4个不相等的实数根,求p的取值范围.
四、解答题(共4题;共41分)
20.(14分)(2025九上·淮南期末)已知抛物线与x轴的一个交点为,与y轴的交点为.
(1)(7分)求抛物线的解析式;
(2)(7分)求y的最值.
21.(13分)(2024八下·浦东期中)已知一次函数平行于直线,且与函数有一个交点,求:
(1)(7分)一次函数的解析式.
(2)(6分)此一次函数与两坐标轴围成的三角形面积.
22.(7分)(2023九上·澧县月考)今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且,,靠背,支架,扶手的一部分.这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:,,)
23.(7分)(2023·兴宁模拟)在平面直角坐标系xOy中,抛物线y=a(x﹣3)(x+1)与x轴交于A、B两点,与y轴交于点C(0,),连接AC、BC.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点E为第二象限抛物线上的一动点,EF∥BC,直线EF与抛物线交于点F,设直线EF的表达式为y=kx+b.
①如图①,直线y=kx+b与抛物线对称轴交于点G,若△DGF∽△BDC,求k、b的值;
②如图②,直线y=kx+b与y轴交于点M,与直线y=x交于点H,若﹣=,求b的值.
答案解析部分
1.【答案】D
【知识点】相似三角形的应用
2.【答案】A
【知识点】反比例函数的性质
3.【答案】C
【知识点】相似三角形的判定与性质
4.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
5.【答案】D
【知识点】反比例函数图象的对称性;反比例函数的性质
6.【答案】D
【知识点】二次函数图象与系数的关系;一次函数图象、性质与系数的关系
7.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
8.【答案】A
【知识点】反比例函数的性质;待定系数法求反比例函数解析式
9.【答案】A
【知识点】反比例函数的图象;三角形的面积
10.【答案】D
【知识点】线段垂直平分线的性质;相似三角形的判定
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】
【知识点】勾股定理;解直角三角形的实际应用﹣坡度坡角问题
14.【答案】
【知识点】比例的性质
15.【答案】
【知识点】正方形的性质;二次函数-动态几何问题
16.【答案】
【知识点】等边三角形的判定与性质;矩形的性质;解直角三角形
17.【答案】(1)4;(2)
【知识点】零指数幂;负整数指数幂;解一元一次不等式组;求特殊角的三角函数值
18.【答案】米
【知识点】解直角三角形的实际应用﹣坡度坡角问题;解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)
(2)
(3)或
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
20.【答案】(1)
(2)
【知识点】二次函数的最值;待定系数法求二次函数解析式
21.【答案】(1)
(2)
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系;反比例函数与一次函数的交点问题
22.【答案】解:方法一:
过点作交的延长线于点,
四边形是平行四边形,,
,
,
过点作于点,
由题意知,,
,
又,
,
过作于点,
,,
,
,
靠背顶端点距地面高度为
;
方法二:
如图,过点作交的延长线于点,过点作于点,延长交于点,
,,
,
又,
,
,
,
过作于,
由题意知,,
,
又,
,
靠背顶端点距地面高度为.
【知识点】平行线的性质;平行四边形的性质;解直角三角形的其他实际应用
23.【答案】(1)y=x2﹣x﹣;(2)①k=,b=;②2
【知识点】一元二次方程的根与系数的关系(韦达定理);待定系数法求二次函数解析式;相似三角形的判定与性质;解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
