数学备战考试优质试题100例 专题5.3不等式(第02期)(必修5)解析版 Word版含解析
文档属性
| 名称 | 数学备战考试优质试题100例 专题5.3不等式(第02期)(必修5)解析版 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-10 20:44:46 | ||
图片预览



文档简介
1.设,则下列不等式一定成立的是(
)
(A)
(B)
(C)
(D)
【答案】D
( http: / / www.21cnjy.com )考点:不等式的性质.
2.若不等式组
( http: / / www.21cnjy.com ),表示的平面区域是一个三角形区域,则的取值范围是(
)
A.
B.
C.
D.或
【答案】D
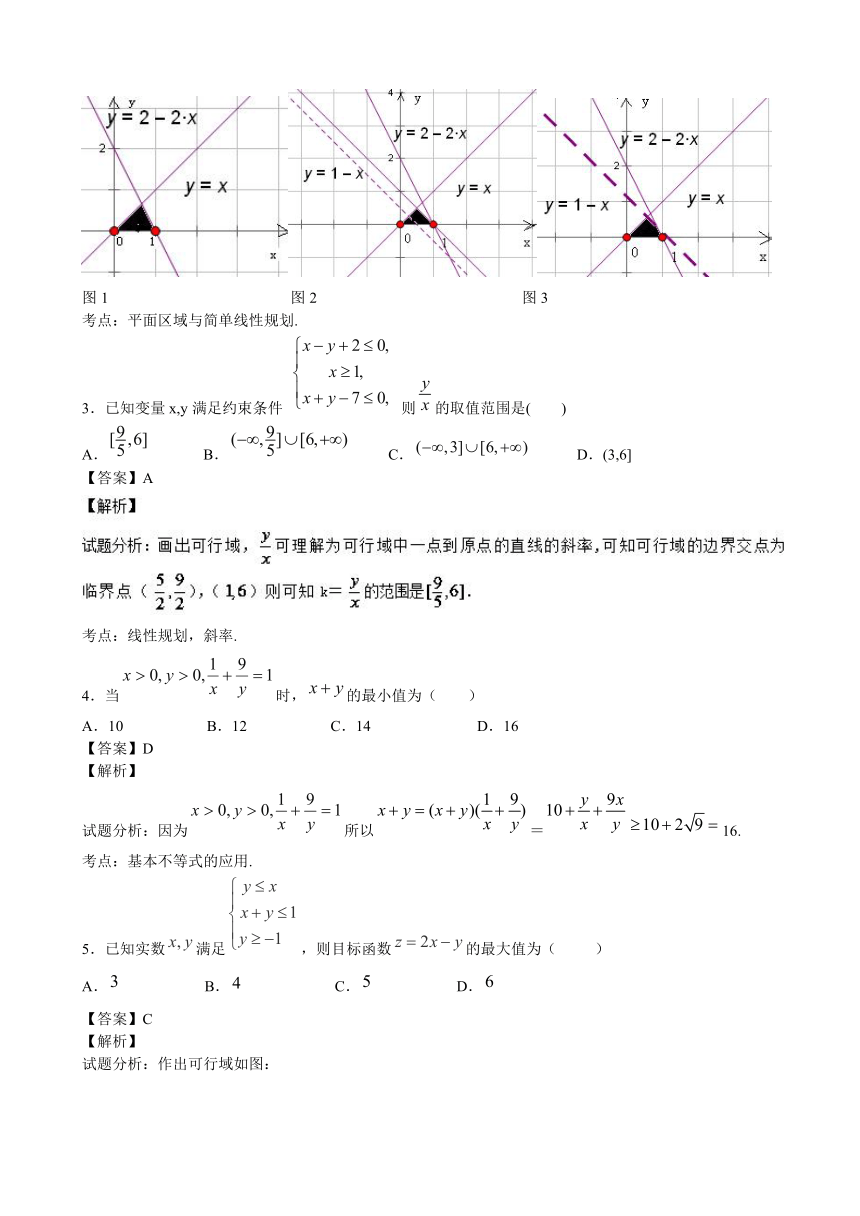
【解析】根据
( http: / / www.21cnjy.com )画出平面区域(如图1所示),由于直线斜率为,纵截距为,
自直线经过原点起,向上平移,当时,
( http: / / www.21cnjy.com )表示的平面区域是一个三角形区域(如图2所示);当时,
( http: / / www.21cnjy.com )表示的平面区域是一个四边形区域(如图3所示),当时,
( http: / / www.21cnjy.com )表示的平面区域是一个三角形区域(如图1所示),故选D.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
图1
图2
图3
考点:平面区域与简单线性规划.
3.已知变量x,y满足约束条件
( http: / / www.21cnjy.com )
则的取值范围是(
)
A.
B.
C.
D.(3,6]
【答案】A
( http: / / www.21cnjy.com )考点:线性规划,斜率.
4.当时,的最小值为(
)
A.10
B.12
C.14
D.16
【答案】D
【解析】
试题分析:因为所以=16.
考点:基本不等式的应用.
5.已知实数满足
( http: / / www.21cnjy.com ),则目标函数的最大值为(
)
A.
B.
C.
D.
【答案】C
【解析】
试题分析:作出可行域如图:
( http: / / www.21cnjy.com )
再作出目标函数线,并平移使之经过可行域,当目标函数线过点时纵截距最小但最大,此时.故C正确.
考点:线性规划问题.
6.不等式的解集是(
)
A.
B.
C.
D.
【答案】C
( http: / / www.21cnjy.com )考点:一元二次不等式的解法
7.(2006 广东)在约束条件
( http: / / www.21cnjy.com )下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
A.
B.
C.
D.
( http: / / www.21cnjy.com )
【答案】D
( http: / / www.21cnjy.com )
考点:简单线性规划的应用.
8.[2014·沈阳四校联考]下列各点中,与点(1,2)位于直线x+y-1=0的同一侧的是( )
A.(0,0)
B.(-1,1)
C.(-1,3)
D.(2,-3)
【答案】C
【解析】点(1,2)使x+y-1>0,
点(-1,3)使x+y-1>0,
∴此两点位于x+y-1=0的同一侧.
9.(5分)(2011 天津)设变量x,y满足约束条件
( http: / / www.21cnjy.com )则目标函数z=3x﹣y的最大值为(
)
A.﹣4
B.0
C.
D.4
【答案】D
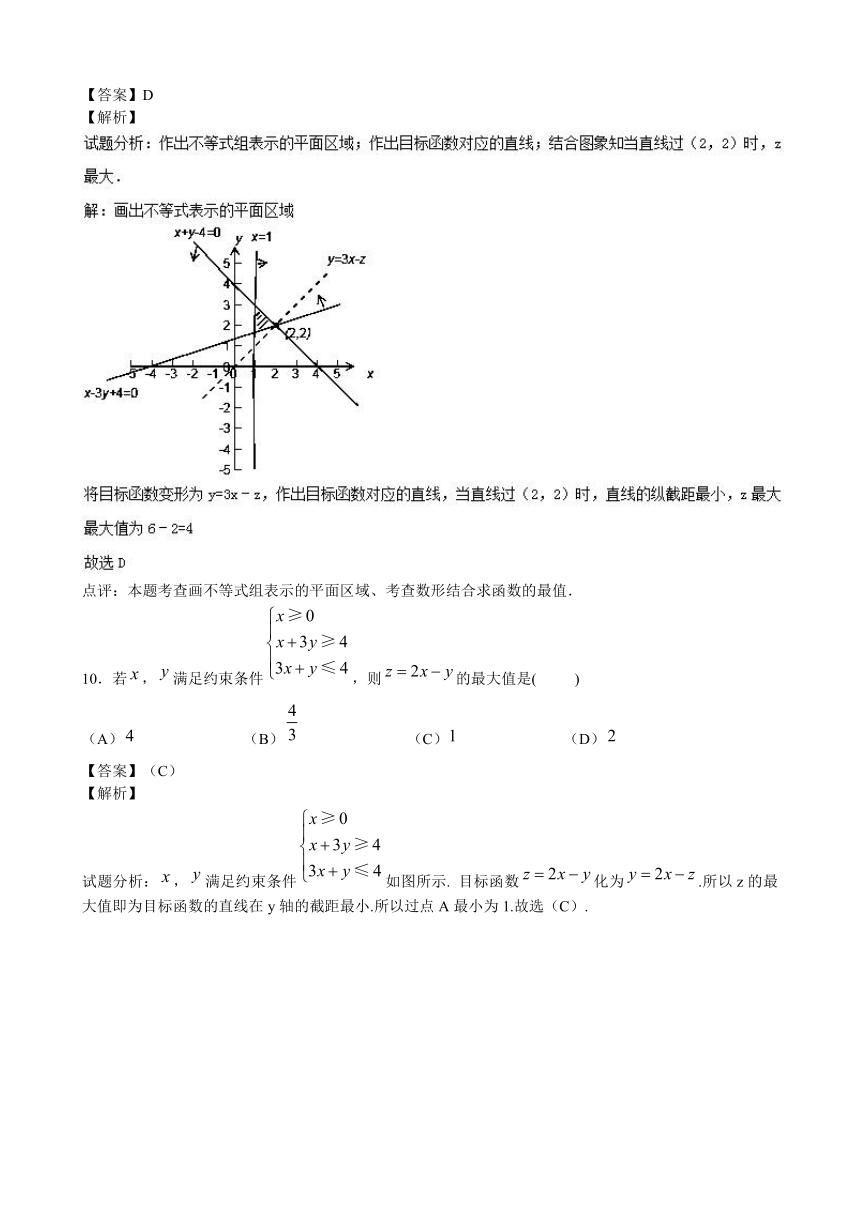
【解析】
( http: / / www.21cnjy.com )点评:本题考查画不等式组表示的平面区域、考查数形结合求函数的最值.
10.若,满足约束条件
( http: / / www.21cnjy.com ),则的最大值是(
)
(A)
(B)
(C)
(D)
【答案】(C)
【解析】
试题分析:,满足约束条件
( http: / / www.21cnjy.com )如图所示.
目标函数化为.所以z的最大值即为目标函数的直线在y轴的截距最小.所以过点A最小为1.故选(C).
( http: / / www.21cnjy.com )
考点:1.线性规划的知识.2.数学结合的数学思想.
11.已知点与点在直线的两侧,且,
则的取值范围是(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )考点:简单线性规划
12.已知点与点在直线的两侧,且,
则的取值范围是(
)
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )
考点:简单线性规划的应用,直线的斜率计算公式.
13.实数x,y满足约束条件
( http: / / www.21cnjy.com ),则的最小值是(
)
A.5
B.–6
C.10
D.–10
【答案】B
【解析】
试题分析:约束条件
( http: / / www.21cnjy.com )对应的平面区域如下图示:
( http: / / www.21cnjy.com )
当直线z=2x+4y过(3,-3)时,Z取得最小值-6.
故选B.
考点:简单线性规划.
14.若实数满足
( http: / / www.21cnjy.com ),则的值域是( )
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
15.在平面直角坐标系xOy中,M为不等式组
( http: / / www.21cnjy.com )所表示的区域上一动点,则的最小值为(
)
A.
2
B.
1
C.
D.
【答案】C
( http: / / www.21cnjy.com )
16.若,则的最小值为(
)
A.
1
B.
2
C.
3
D.
4
【答案】D
【解析】,当且仅当,即,即时取等号,所以最小值为4,选D.
17.已知,则的最小值是( )
A.
4
B.
3
C.
2
D.
1
【答案】A
( http: / / www.21cnjy.com )
18.不等式的解集是( )
A.
B.
C.
D.
【答案】B
【解析】,数轴标根得:,选B.
19.已知集合,则下列结论正确的是(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )
20.若不等式对满足的所有都成立,则x的取值范围是(
)
A.
B.
C.
D.
【答案】D
【解析】不等式化为:,令,则时,恒成立
所以只需即,
所以x的范围是,选D.
21.若不等式的解集是R,则m的范围是( )
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )22.若为实数,则下列命题正确的是(
)
A.若,则
B.若,则
C.若,则
D.若,则
【答案】B
【解析】
试题分析.
A
若,则不成立;C
对两边都除以,可得,C不成立;D令则有所以D不成立,故选B.
考点:不等式的基本性质.
23.已知点M(x,y)是平面区域
( http: / / www.21cnjy.com )内的动点,则的最大值是(
)
(A)10
(B)
(C)
(D)13
【答案】D
【解析】
试题分析:解:
点M(x,y)所在的平面区域
( http: / / www.21cnjy.com )如下图中的阴影部分,设点
的坐标为
由图可知当最大时,点M应在线段上;而
( http: / / www.21cnjy.com )
的最大值是13.
故应选D.
考点:1、二元一次不等式(组)所表示的平面区域;2、两点间的距离公式.
24.不等式的解集为(
)
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )考点:分式不等式
25.函数的定义域为(
)
A.
B.
C.
D.
【答案】A
【解析】
试题分析:由二次根式的定义可得,所以函数的定义域为,故选A.
考点:定义域
一次不等式
26.下列命题正确的是(
)
A.若,则
B.若则
C.若,则
D.若,则
【答案】D
( http: / / www.21cnjy.com )考点:1.基本不等式的应用.2.三角函数的知识.3.对数的知识.4.不等式的性质.
27.设变量满足,则的最大值和最小值分别为(
)
A.1,-1
B.2,-2
C.1,-2
D.2,-1
【答案】B
【解析】
试题分析:变量满足的区域如图所示:
( http: / / www.21cnjy.com )
当过点A(1,0)时,z最大,当过点B(-1,0)时,z最小,
即最大值为2,最小值为-2.
考点:线性规划.
28.已知函数,数列满足,且数列是递增数列,则实数的取值范围是
(
)
(A)
(B)
(C)
(D)
【答案】C
【解析】
试题分析:由题意得:解得或因此.
考点:分段函数单调性,数列单调性
29.已知,若是的充分不必要条件,则实数的取值范围为(
)
A.(-∞,3]
B.[2,3]
C.(2,3]
D.(2,3)
【答案】C
( http: / / www.21cnjy.com )考点:必要条件、充分条件与充要条件的判断.
30.已知,且,则下列结论恒成立的是
(
).
A.
B.
C.
D.
【答案】C
【解析】
试题分析:当都是负数时,不成立,当一正一负时,不成立,当时,不成立,因此只有是正确的.
考点:基本不等式.
31.已知集合,,则=(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )考点:1.一元二次不等式的解法;2.绝对值不等式的解法;3.集合的运算.
32.设、,若,则下列不等式中正确的是(
)
A.
B.
C.
D.
【答案】D
【解析】
试题分析:当时,,当时,,∴,∴,
考点:不等式的性质.
33.原点和点在直线
的两侧,则实数的
取值范围是
A.
B.
C.
或
D.
或
【答案】B
【解析】
试题分析:分别把原点和点代入直线得到不等式组,
所以,选B
考点:点位于直线两侧的充要条件
34.设,则下列不等式中一定成立的是
A.
B.
C.
D.
【答案】A
【解析】
试题分析:A.
故A正确;B中,故B不正确,D中,故D不正确;C中当,故C不正确
考点:不等式的性质
35.不等式的解集是
A.
B.
C.
D.
【答案】B
【解析】
试题分析:
考点:分式不等式的解法
36.若原点和点分别在直线的两侧,则的取值范围是
A.
B.
C.或
D.或
【答案】B
( http: / / www.21cnjy.com )考点:点位于直线两侧的充要条件
37.设,则下列不等式一定成立的是
A.
B.
C.
D.
【答案】A
【解析】
试题分析:A.
故A正确;B中,故B不正确,D中,故D不正确;C中当,故C不正确
考点:不等式的性质
38.已知不等式的解集为,则不等式的解集为(
)
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )考点:本题考查一元二次不等式的解法.
39.已知,则下列推证中正确的是(
)
A.
B.
C.
D.
【答案】C
【解析】
试题分析:A
当时不成立;B
当时不成立;D
当均为负值时,不成立.
考点:本题主要考查不等式的性质.
40.设变量、满足约束条件
( http: / / www.21cnjy.com )则目标函数的最小值是(
)
A.-7
B.-4
C.1
D.2
【答案】A
【解析】
试题分析:
( http: / / www.21cnjy.com )
法一:由可得交点C,由可得交点B,由可得交点A,分别代入目标函数可得最小值-7.法二:画出如上图像,数形在结合易得B处取得最小值.
考点:本题主要考简单的线性规划问题.
41.设非零实数满足,则下列不等式中一定成立的是(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )考点:不等式的性质.
42.实数、满足
( http: / / www.21cnjy.com )
则=的取值范围是(
)
A.
[-1,0]
B.
-∞,0]
C.
[-1,+∞
D.
[-1,1
【答案】D
【解析】
试题分析:作出满足不等式组约束条件的平面区域,如下图所示:
( http: / / www.21cnjy.com )
∵表示区域内点与点连线的斜率,又∵当,时,,直线与平行时,,∴的取值范围为,故选D.
考点:1、简单的线性规划;2、直线斜率.
43.已知满足不等式
( http: / / www.21cnjy.com )设,则的最大值与最小值的差为(
)
A.
4
B.
3
C.
2
D.
1
【答案】A
( http: / / www.21cnjy.com )考点:线性规划.
44.若实数满足,则的取值范围是(
)
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )考点:线性规划求最值.
45.若函数满足:,则的最小值为(
)
A.
B.
C.
D.
【答案】
【解析】
试题分析:根据①,有②,由①②联立,消去得,当;当,所以.
考点:方程组思想求函数解析式;均值不等式;
46.若实数满足,则的取值范围是(
)
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )考点:线性规划求最值.
47.已知正数a,b满足4a+b=30,使得取最小值的实数对(a,b)是
A.(5,10)
B.(6,6)
C.(10,5)
D.(7,2)
【答案】A
【解析】
试题分析:由基本不等式可得:()(4a+b)当且仅当时取等号,再由4a+b=30,可解a=5,b=10.
考点:基本不等式的应用.
48.设a、b∈R,若a-|b|>0,则下列不等式中正确的是( )
(A)b-a>0
(B)a3+b3<0
(C)a2-b2<0
(D)b+a>0
【答案】D
【解析】∵a-|b|>0,∴|b|0,
∴-a0.
49.设其中实数满足
( http: / / www.21cnjy.com ),若的最大值为,则的最小值为(
)
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )考点:简单线性规划
50.不等式的解是___________.
【答案】(或)
【解析】
试题分析:可转化为整式不等式,,也可分类讨论即分子与分母异号.
考点:解分式不等式.
51.当时,函数的最小值是_______________.
【答案】3
( http: / / www.21cnjy.com )
考点:均值不等式求最值.
52.已知实数满足约束条件
( http: / / www.21cnjy.com ),则的最小值为
.
【答案】3.
【解析】
试题分析:如图所示,令,当过A点时,Z取到最小值为.
( http: / / www.21cnjy.com )
考点:线性规划问题(求线性目标函数的最小值).
53.若实数,满足线性约束条件,则的最大值为________.
【答案】.
( http: / / www.21cnjy.com )考点:线性规划.
54.已知点在不等式组所表示的平面区域内,则
的最大值为
.
【答案】6.
【解析】
试题分析:画出可行域:
( http: / / www.21cnjy.com ),再画出;平移到经过点B(2,2)时,目标函数z取得最大值为:;故应填6.
考点:线性规划.
55.设x,y满足约束条件:
( http: / / www.21cnjy.com );则z=x﹣2y的最大值为
.
【答案】3
【解析】
试题分析:不等式组表示的平面区域如图所示,当直线z=x﹣2y过点A(3,0)时,在y轴上截距最小,此时z取得最大值3.故答案为:3.
( http: / / www.21cnjy.com )
考点:简单线性规划.
56.[2013·广东六校联考]已知正实数x,y满足xy=1,则(+y)(+x)的最小值为________.
【答案】4
( http: / / www.21cnjy.com )57.已知实数,满足条件
( http: / / www.21cnjy.com )
则的最大值为
.
【答案】
【解析】
试题分析:可行域为三角形OAB及其内部,其中.当曲线过点B时,取最大值
( http: / / www.21cnjy.com )
考点:线性规划求最值
58.若不等式对任意正实数恒成立,则正实数的最小值为
.
【答案】4
【解析】
试题分析:,,因此最小值为4.
考点:基本不等式.
59.设
a∈R,若x>0时均有,则a=
【答案】
( http: / / www.21cnjy.com )60.已知,,则的最小值为
.
【答案】3
( http: / / www.21cnjy.com )考点:基本不等式及其应用.
61.不等式的解集为____________.
【答案】
【解析】
试题分析:原不等式可化为,故解集为.
考点:一元二次不等式的解法.
62.不等式的解集为____________.
【答案】
【解析】
试题分析:原不等式可化为,故解集为.
考点:一元二次不等式的解法.
63.已知实数、满足不等式组
( http: / / www.21cnjy.com ),则的最大值是____________.
【答案】20
【解析】
试题分析:作出不等式组表示的可行域,如图四边形内部(含边界),作直线,平移直线,当过点时,取得最大值20.
( http: / / www.21cnjy.com )
考点:线性规划.
64.已知偶函数f(x)在[0,∞)上是增函数,则不等式的解集是
【答案】
( http: / / www.21cnjy.com )考点:1.偶函数的性质;2.解不等式.
65.观察下列不等式:1>,1++>1,1+++
+>,1+++
+>2,1+++
+>,
,由此猜测第n个不等式为
(n∈N
).
【答案】1+++
+>
【解析】
试题分析:观察给出的不等式,;;;
,;
由此猜测第n个不等式为.
考点:归纳推理
66.在平面直角坐标系中,若点到直线的距离为,且点在不等式表示的平面区域内,则
.
【答案】6
( http: / / www.21cnjy.com )
考点:二元一次不等式(组)与平面区域.
67.若x,y满足约束条件
( http: / / www.21cnjy.com ),则的最大值是.
【答案】0
【解析】约束条件
( http: / / www.21cnjy.com )的可行域如图所示,即△ABC部分,
HYPERLINK
"http://www.21cnjy.com"
目标函数过A(0,O3)时值最大,最大值为1-1=0.
【考点】线性规划.
68.函数的最小值为.
【答案】2
【解析】
试题分析:由于,所以由重要不等式得.
考点:重要不等式及指数函数.
69.函数的最小值为_____.
【答案】3
【解析】
试题分析:
考点:基本不等式.
70.已知向量=(x,2),=(1,y),其中x>0,y>0.若 =4,则+的最小值为
.
【答案】
( http: / / www.21cnjy.com )考点:基本不等式求最值
71.已知正数满足,则的最小值为
.
【答案】9
【解析】
试题分析:由,得
,当且仅当,即,也即时等号成立,故最小值是9.
考点:基本不等式.
72.已知,函数的图象过(0,1)点,则的最小值是______.
【答案】
【解析】
试题分析:因为函数过点,把点带入函数可得,所以.当且仅当时取等号.故填
考点:基本不等式
73.函数的图象恒过定点A,若点A在直线上,其中,则的最小值为_______.
【答案】
( http: / / www.21cnjy.com )
考点:对数函数的图象和性质,基本不等式的应用.
74.设实数满足不等式组
( http: / / www.21cnjy.com )则的取值范围是
.
【答案】
【解析】如图,已知不等式组表示的平面区域是内部(含边界),表示的是此区域内点到原点距离的平方,从图中可知这个距离的最小值为1,最大值为2,因此的取值范围是.
( http: / / www.21cnjy.com )
【考点】不等式组表示的区域.
75.函数,的值域为_________.
【答案】
( http: / / www.21cnjy.com )考点:本题主要考查分离变量法求函数的值域,不等式的性质.
76.若关于的不等式的解集为,则实数的取值范围是
【答案】
【解析】
试题分析:当时,恒成立;当时,,故
考点:一元二次不等式的解法
77.若变量、满足约束条件
( http: / / www.21cnjy.com ),则的最大值为
.
【答案】1
【解析】
试题分析:可行域为如图所示三角形内部(包括边界)
( http: / / www.21cnjy.com )
则
考点:线性规划问题
78.设变量满足约束条件
( http: / / www.21cnjy.com )则的取值范围是.
( http: / / www.21cnjy.com )
【答案】
考点:线性规划问题
79.对于实数和,定义运算“”:,设,且关于的方程为恰有三个互不相等的实数根,则的取值范围是___________.
【答案】
【解析】
试题分析:由定义运算“
”可知
( http: / / www.21cnjy.com )
,画出该函数的图像
( http: / / www.21cnjy.com )
如图所示,从而可得,又因为要有三个不同的解,所以,所以,所以的取值范围是.
考点:1.函数的零点;2.新定义新运算;3.基本不等式.
80.若实数满足条件
( http: / / www.21cnjy.com ),则的最大值是________.
【答案】
( http: / / www.21cnjy.com )考点:线性规划.
81.已知,若存在,使得任意恒成立,且两边等号能取到,则的最小值为
.
【答案】
【解析】
试题分析:
,对于任意恒成立,即为函数的最小值,为函数的最大值;若两边等号能取到,则至少为的一个周期,所以最小值为.
考点:三角恒等变换、不等式恒成立问题.
82.已知变量满足约束条件
( http: / / www.21cnjy.com )则的最大值是_________.
【答案】
【解析】可行域表示为三角形及其内部,
因此直线过点时取最大值:
考点:线性规划求范围
83.已知变量满足约束条件
( http: / / www.21cnjy.com )则的取值范围是_________.
【答案】,
( http: / / www.21cnjy.com )考点:线性规划求范围
84.已知正数满足,则的最小值为
.
【答案】9
【解析】
试题分析:因为,当且仅当即时取等号,所以的最小值为9.
考点:基本不等式求最值
85.在平面直角坐标系xOy中,P为不等式组
( http: / / www.21cnjy.com )所表示的平面区域内一动点,则线段|OP|的最小值等于
.
【答案】
【解析】
( http: / / www.21cnjy.com )
考点:线性规划
距离最小
86.不等式解集是_____________________.
【答案】
【解析】
试题分析:设,则
( http: / / www.21cnjy.com ).由,解得,所以解集为
考点:分段函数图像
不等式
87.若实数
( http: / / www.21cnjy.com ),
则目标函数的最大值是
.
【答案】2
( http: / / www.21cnjy.com )考点:线性规划问题。
88.若,则的最小值为
;
【答案】4
【解析】
试题分析:因为所以,当且仅当即时取。
考点:基本不等式。
89.函数y=x+(x≠0)的值域是________.
【答案】(-∞,-4]∪[4,+∞)
【解析】当x>0时,y=x+≥2=4,当x<0时,y=x+=-≤-2=-4.
90.设常数a>0,若9x+≥a+1对一切正实数x成立,则a的取值范围为________.
【答案】
【解析】9x+≥2
=6a,所以6a≥a+1,即a≥
91.不等式组
( http: / / www.21cnjy.com )所表示的平面区域的面积是________.
【答案】25
( http: / / www.21cnjy.com )92.已知一元二次不等式f(x)<0的解集为,则f(10x)>0的解集为______.
【答案】{x|x<-lg2}
【解析】由条件得-1<10x<,即x<-lg2
93.已知函数,且的解集为.
(1)求的值;
(2)若,且,求证:.
【答案】(1)(2)详见解析
【解析】
试题分析:(1)根据绝对值不等式的公式求的解集,因为解集又为,根据对应相等可得的值.(2)由(1)知.根据柯西不等式或基本不等式证明即可.
试题解析:解:(1)因为,
所以等价于,
2分
由有解,得,且其解集为.
4分
又的解集为,故.
(5分)
(2)由(1)知
,又,
7分∴
9分
(或展开运用基本不等式)
∴
.10分
考点:1绝对值不等式;2柯西不等式;3基本不等式.
94.解关于x的不等式:≤
【答案】详见解析
( http: / / www.21cnjy.com )当m>0时,原不等式的解集为
当
1当
m=-1时,原不等式的解集为
当m<-1时,原不等式的解集为
考点:1.分式不等式的解法;2.分类讨论思想.
95.已知关于的不等式
的解集为{x∣x<1或x>b}
(1)求的值
(2)解关于的不等式
【答案】(1)
;(2)
(1,2).
【解析】
( http: / / www.21cnjy.com )考点:一元二次不等式的解法.
96.设是定义在上的偶函数,且当时,.若对任意的,不等式恒成立,
求实数的取值范围
【答案】
( http: / / www.21cnjy.com )
若由(2)得成立,则时恒成立,即
,
14分
实数的取值范围
15分
考点:
分段函数,不等式恒成立
97.已知函数
(1)求不等式的解集;
(2)若关于的不等式的解集非空,求实数的取值范围.
【答案】(1);(2)或.
( http: / / www.21cnjy.com )考点:1.绝对值的运算性质;2.绝对值不等式的解法.
98.画出不等式组
( http: / / www.21cnjy.com )表示的平面区域.
【答案】如图
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
99.函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围;
(2)当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
【答案】(1)[-6,2](2)[-7,2]
【解析】(1)∵x∈R,f(x)≥a恒成立,
∴x2+ax+3-a≥0恒成立,则Δ=a2-4(3-a)≤0,得-6≤a≤2.
∴当x∈R时,f(x)≥a恒成立,则a的取值范围为[-6,2].
(2)f(x)=+3-.
讨论对称轴与[-2,2]的位置关系,得到a的取值满足下列条件:
( http: / / www.21cnjy.com )或
( http: / / www.21cnjy.com )或
( http: / / www.21cnjy.com )
即或或
解得-7≤a≤2.∴当x∈[-2,2]时,f(x)≥a恒成立,则a的取值范围为[-7,2].
100.解关于x的不等式(1-ax)2<1.
【答案】当a<0时,原不等式解集为;当a>0时,原不等式解集为
( http: / / www.21cnjy.com )
A(1,1)
B(0,3)
C
x
y
O
)
(A)
(B)
(C)
(D)
【答案】D
( http: / / www.21cnjy.com )考点:不等式的性质.
2.若不等式组
( http: / / www.21cnjy.com ),表示的平面区域是一个三角形区域,则的取值范围是(
)
A.
B.
C.
D.或
【答案】D
【解析】根据
( http: / / www.21cnjy.com )画出平面区域(如图1所示),由于直线斜率为,纵截距为,
自直线经过原点起,向上平移,当时,
( http: / / www.21cnjy.com )表示的平面区域是一个三角形区域(如图2所示);当时,
( http: / / www.21cnjy.com )表示的平面区域是一个四边形区域(如图3所示),当时,
( http: / / www.21cnjy.com )表示的平面区域是一个三角形区域(如图1所示),故选D.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
图1
图2
图3
考点:平面区域与简单线性规划.
3.已知变量x,y满足约束条件
( http: / / www.21cnjy.com )
则的取值范围是(
)
A.
B.
C.
D.(3,6]
【答案】A
( http: / / www.21cnjy.com )考点:线性规划,斜率.
4.当时,的最小值为(
)
A.10
B.12
C.14
D.16
【答案】D
【解析】
试题分析:因为所以=16.
考点:基本不等式的应用.
5.已知实数满足
( http: / / www.21cnjy.com ),则目标函数的最大值为(
)
A.
B.
C.
D.
【答案】C
【解析】
试题分析:作出可行域如图:
( http: / / www.21cnjy.com )
再作出目标函数线,并平移使之经过可行域,当目标函数线过点时纵截距最小但最大,此时.故C正确.
考点:线性规划问题.
6.不等式的解集是(
)
A.
B.
C.
D.
【答案】C
( http: / / www.21cnjy.com )考点:一元二次不等式的解法
7.(2006 广东)在约束条件
( http: / / www.21cnjy.com )下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
A.
B.
C.
D.
( http: / / www.21cnjy.com )
【答案】D
( http: / / www.21cnjy.com )
考点:简单线性规划的应用.
8.[2014·沈阳四校联考]下列各点中,与点(1,2)位于直线x+y-1=0的同一侧的是( )
A.(0,0)
B.(-1,1)
C.(-1,3)
D.(2,-3)
【答案】C
【解析】点(1,2)使x+y-1>0,
点(-1,3)使x+y-1>0,
∴此两点位于x+y-1=0的同一侧.
9.(5分)(2011 天津)设变量x,y满足约束条件
( http: / / www.21cnjy.com )则目标函数z=3x﹣y的最大值为(
)
A.﹣4
B.0
C.
D.4
【答案】D
【解析】
( http: / / www.21cnjy.com )点评:本题考查画不等式组表示的平面区域、考查数形结合求函数的最值.
10.若,满足约束条件
( http: / / www.21cnjy.com ),则的最大值是(
)
(A)
(B)
(C)
(D)
【答案】(C)
【解析】
试题分析:,满足约束条件
( http: / / www.21cnjy.com )如图所示.
目标函数化为.所以z的最大值即为目标函数的直线在y轴的截距最小.所以过点A最小为1.故选(C).
( http: / / www.21cnjy.com )
考点:1.线性规划的知识.2.数学结合的数学思想.
11.已知点与点在直线的两侧,且,
则的取值范围是(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )考点:简单线性规划
12.已知点与点在直线的两侧,且,
则的取值范围是(
)
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )
考点:简单线性规划的应用,直线的斜率计算公式.
13.实数x,y满足约束条件
( http: / / www.21cnjy.com ),则的最小值是(
)
A.5
B.–6
C.10
D.–10
【答案】B
【解析】
试题分析:约束条件
( http: / / www.21cnjy.com )对应的平面区域如下图示:
( http: / / www.21cnjy.com )
当直线z=2x+4y过(3,-3)时,Z取得最小值-6.
故选B.
考点:简单线性规划.
14.若实数满足
( http: / / www.21cnjy.com ),则的值域是( )
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
15.在平面直角坐标系xOy中,M为不等式组
( http: / / www.21cnjy.com )所表示的区域上一动点,则的最小值为(
)
A.
2
B.
1
C.
D.
【答案】C
( http: / / www.21cnjy.com )
16.若,则的最小值为(
)
A.
1
B.
2
C.
3
D.
4
【答案】D
【解析】,当且仅当,即,即时取等号,所以最小值为4,选D.
17.已知,则的最小值是( )
A.
4
B.
3
C.
2
D.
1
【答案】A
( http: / / www.21cnjy.com )
18.不等式的解集是( )
A.
B.
C.
D.
【答案】B
【解析】,数轴标根得:,选B.
19.已知集合,则下列结论正确的是(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )
20.若不等式对满足的所有都成立,则x的取值范围是(
)
A.
B.
C.
D.
【答案】D
【解析】不等式化为:,令,则时,恒成立
所以只需即,
所以x的范围是,选D.
21.若不等式的解集是R,则m的范围是( )
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )22.若为实数,则下列命题正确的是(
)
A.若,则
B.若,则
C.若,则
D.若,则
【答案】B
【解析】
试题分析.
A
若,则不成立;C
对两边都除以,可得,C不成立;D令则有所以D不成立,故选B.
考点:不等式的基本性质.
23.已知点M(x,y)是平面区域
( http: / / www.21cnjy.com )内的动点,则的最大值是(
)
(A)10
(B)
(C)
(D)13
【答案】D
【解析】
试题分析:解:
点M(x,y)所在的平面区域
( http: / / www.21cnjy.com )如下图中的阴影部分,设点
的坐标为
由图可知当最大时,点M应在线段上;而
( http: / / www.21cnjy.com )
的最大值是13.
故应选D.
考点:1、二元一次不等式(组)所表示的平面区域;2、两点间的距离公式.
24.不等式的解集为(
)
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )考点:分式不等式
25.函数的定义域为(
)
A.
B.
C.
D.
【答案】A
【解析】
试题分析:由二次根式的定义可得,所以函数的定义域为,故选A.
考点:定义域
一次不等式
26.下列命题正确的是(
)
A.若,则
B.若则
C.若,则
D.若,则
【答案】D
( http: / / www.21cnjy.com )考点:1.基本不等式的应用.2.三角函数的知识.3.对数的知识.4.不等式的性质.
27.设变量满足,则的最大值和最小值分别为(
)
A.1,-1
B.2,-2
C.1,-2
D.2,-1
【答案】B
【解析】
试题分析:变量满足的区域如图所示:
( http: / / www.21cnjy.com )
当过点A(1,0)时,z最大,当过点B(-1,0)时,z最小,
即最大值为2,最小值为-2.
考点:线性规划.
28.已知函数,数列满足,且数列是递增数列,则实数的取值范围是
(
)
(A)
(B)
(C)
(D)
【答案】C
【解析】
试题分析:由题意得:解得或因此.
考点:分段函数单调性,数列单调性
29.已知,若是的充分不必要条件,则实数的取值范围为(
)
A.(-∞,3]
B.[2,3]
C.(2,3]
D.(2,3)
【答案】C
( http: / / www.21cnjy.com )考点:必要条件、充分条件与充要条件的判断.
30.已知,且,则下列结论恒成立的是
(
).
A.
B.
C.
D.
【答案】C
【解析】
试题分析:当都是负数时,不成立,当一正一负时,不成立,当时,不成立,因此只有是正确的.
考点:基本不等式.
31.已知集合,,则=(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )考点:1.一元二次不等式的解法;2.绝对值不等式的解法;3.集合的运算.
32.设、,若,则下列不等式中正确的是(
)
A.
B.
C.
D.
【答案】D
【解析】
试题分析:当时,,当时,,∴,∴,
考点:不等式的性质.
33.原点和点在直线
的两侧,则实数的
取值范围是
A.
B.
C.
或
D.
或
【答案】B
【解析】
试题分析:分别把原点和点代入直线得到不等式组,
所以,选B
考点:点位于直线两侧的充要条件
34.设,则下列不等式中一定成立的是
A.
B.
C.
D.
【答案】A
【解析】
试题分析:A.
故A正确;B中,故B不正确,D中,故D不正确;C中当,故C不正确
考点:不等式的性质
35.不等式的解集是
A.
B.
C.
D.
【答案】B
【解析】
试题分析:
考点:分式不等式的解法
36.若原点和点分别在直线的两侧,则的取值范围是
A.
B.
C.或
D.或
【答案】B
( http: / / www.21cnjy.com )考点:点位于直线两侧的充要条件
37.设,则下列不等式一定成立的是
A.
B.
C.
D.
【答案】A
【解析】
试题分析:A.
故A正确;B中,故B不正确,D中,故D不正确;C中当,故C不正确
考点:不等式的性质
38.已知不等式的解集为,则不等式的解集为(
)
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )考点:本题考查一元二次不等式的解法.
39.已知,则下列推证中正确的是(
)
A.
B.
C.
D.
【答案】C
【解析】
试题分析:A
当时不成立;B
当时不成立;D
当均为负值时,不成立.
考点:本题主要考查不等式的性质.
40.设变量、满足约束条件
( http: / / www.21cnjy.com )则目标函数的最小值是(
)
A.-7
B.-4
C.1
D.2
【答案】A
【解析】
试题分析:
( http: / / www.21cnjy.com )
法一:由可得交点C,由可得交点B,由可得交点A,分别代入目标函数可得最小值-7.法二:画出如上图像,数形在结合易得B处取得最小值.
考点:本题主要考简单的线性规划问题.
41.设非零实数满足,则下列不等式中一定成立的是(
)
A.
B.
C.
D.
【答案】D
( http: / / www.21cnjy.com )考点:不等式的性质.
42.实数、满足
( http: / / www.21cnjy.com )
则=的取值范围是(
)
A.
[-1,0]
B.
-∞,0]
C.
[-1,+∞
D.
[-1,1
【答案】D
【解析】
试题分析:作出满足不等式组约束条件的平面区域,如下图所示:
( http: / / www.21cnjy.com )
∵表示区域内点与点连线的斜率,又∵当,时,,直线与平行时,,∴的取值范围为,故选D.
考点:1、简单的线性规划;2、直线斜率.
43.已知满足不等式
( http: / / www.21cnjy.com )设,则的最大值与最小值的差为(
)
A.
4
B.
3
C.
2
D.
1
【答案】A
( http: / / www.21cnjy.com )考点:线性规划.
44.若实数满足,则的取值范围是(
)
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )考点:线性规划求最值.
45.若函数满足:,则的最小值为(
)
A.
B.
C.
D.
【答案】
【解析】
试题分析:根据①,有②,由①②联立,消去得,当;当,所以.
考点:方程组思想求函数解析式;均值不等式;
46.若实数满足,则的取值范围是(
)
A.
B.
C.
D.
【答案】A
( http: / / www.21cnjy.com )考点:线性规划求最值.
47.已知正数a,b满足4a+b=30,使得取最小值的实数对(a,b)是
A.(5,10)
B.(6,6)
C.(10,5)
D.(7,2)
【答案】A
【解析】
试题分析:由基本不等式可得:()(4a+b)当且仅当时取等号,再由4a+b=30,可解a=5,b=10.
考点:基本不等式的应用.
48.设a、b∈R,若a-|b|>0,则下列不等式中正确的是( )
(A)b-a>0
(B)a3+b3<0
(C)a2-b2<0
(D)b+a>0
【答案】D
【解析】∵a-|b|>0,∴|b|
∴-a
49.设其中实数满足
( http: / / www.21cnjy.com ),若的最大值为,则的最小值为(
)
A.
B.
C.
D.
【答案】B
( http: / / www.21cnjy.com )考点:简单线性规划
50.不等式的解是___________.
【答案】(或)
【解析】
试题分析:可转化为整式不等式,,也可分类讨论即分子与分母异号.
考点:解分式不等式.
51.当时,函数的最小值是_______________.
【答案】3
( http: / / www.21cnjy.com )
考点:均值不等式求最值.
52.已知实数满足约束条件
( http: / / www.21cnjy.com ),则的最小值为
.
【答案】3.
【解析】
试题分析:如图所示,令,当过A点时,Z取到最小值为.
( http: / / www.21cnjy.com )
考点:线性规划问题(求线性目标函数的最小值).
53.若实数,满足线性约束条件,则的最大值为________.
【答案】.
( http: / / www.21cnjy.com )考点:线性规划.
54.已知点在不等式组所表示的平面区域内,则
的最大值为
.
【答案】6.
【解析】
试题分析:画出可行域:
( http: / / www.21cnjy.com ),再画出;平移到经过点B(2,2)时,目标函数z取得最大值为:;故应填6.
考点:线性规划.
55.设x,y满足约束条件:
( http: / / www.21cnjy.com );则z=x﹣2y的最大值为
.
【答案】3
【解析】
试题分析:不等式组表示的平面区域如图所示,当直线z=x﹣2y过点A(3,0)时,在y轴上截距最小,此时z取得最大值3.故答案为:3.
( http: / / www.21cnjy.com )
考点:简单线性规划.
56.[2013·广东六校联考]已知正实数x,y满足xy=1,则(+y)(+x)的最小值为________.
【答案】4
( http: / / www.21cnjy.com )57.已知实数,满足条件
( http: / / www.21cnjy.com )
则的最大值为
.
【答案】
【解析】
试题分析:可行域为三角形OAB及其内部,其中.当曲线过点B时,取最大值
( http: / / www.21cnjy.com )
考点:线性规划求最值
58.若不等式对任意正实数恒成立,则正实数的最小值为
.
【答案】4
【解析】
试题分析:,,因此最小值为4.
考点:基本不等式.
59.设
a∈R,若x>0时均有,则a=
【答案】
( http: / / www.21cnjy.com )60.已知,,则的最小值为
.
【答案】3
( http: / / www.21cnjy.com )考点:基本不等式及其应用.
61.不等式的解集为____________.
【答案】
【解析】
试题分析:原不等式可化为,故解集为.
考点:一元二次不等式的解法.
62.不等式的解集为____________.
【答案】
【解析】
试题分析:原不等式可化为,故解集为.
考点:一元二次不等式的解法.
63.已知实数、满足不等式组
( http: / / www.21cnjy.com ),则的最大值是____________.
【答案】20
【解析】
试题分析:作出不等式组表示的可行域,如图四边形内部(含边界),作直线,平移直线,当过点时,取得最大值20.
( http: / / www.21cnjy.com )
考点:线性规划.
64.已知偶函数f(x)在[0,∞)上是增函数,则不等式的解集是
【答案】
( http: / / www.21cnjy.com )考点:1.偶函数的性质;2.解不等式.
65.观察下列不等式:1>,1++>1,1+++
+>,1+++
+>2,1+++
+>,
,由此猜测第n个不等式为
(n∈N
).
【答案】1+++
+>
【解析】
试题分析:观察给出的不等式,;;;
,;
由此猜测第n个不等式为.
考点:归纳推理
66.在平面直角坐标系中,若点到直线的距离为,且点在不等式表示的平面区域内,则
.
【答案】6
( http: / / www.21cnjy.com )
考点:二元一次不等式(组)与平面区域.
67.若x,y满足约束条件
( http: / / www.21cnjy.com ),则的最大值是.
【答案】0
【解析】约束条件
( http: / / www.21cnjy.com )的可行域如图所示,即△ABC部分,
HYPERLINK
"http://www.21cnjy.com"
目标函数过A(0,O3)时值最大,最大值为1-1=0.
【考点】线性规划.
68.函数的最小值为.
【答案】2
【解析】
试题分析:由于,所以由重要不等式得.
考点:重要不等式及指数函数.
69.函数的最小值为_____.
【答案】3
【解析】
试题分析:
考点:基本不等式.
70.已知向量=(x,2),=(1,y),其中x>0,y>0.若 =4,则+的最小值为
.
【答案】
( http: / / www.21cnjy.com )考点:基本不等式求最值
71.已知正数满足,则的最小值为
.
【答案】9
【解析】
试题分析:由,得
,当且仅当,即,也即时等号成立,故最小值是9.
考点:基本不等式.
72.已知,函数的图象过(0,1)点,则的最小值是______.
【答案】
【解析】
试题分析:因为函数过点,把点带入函数可得,所以.当且仅当时取等号.故填
考点:基本不等式
73.函数的图象恒过定点A,若点A在直线上,其中,则的最小值为_______.
【答案】
( http: / / www.21cnjy.com )
考点:对数函数的图象和性质,基本不等式的应用.
74.设实数满足不等式组
( http: / / www.21cnjy.com )则的取值范围是
.
【答案】
【解析】如图,已知不等式组表示的平面区域是内部(含边界),表示的是此区域内点到原点距离的平方,从图中可知这个距离的最小值为1,最大值为2,因此的取值范围是.
( http: / / www.21cnjy.com )
【考点】不等式组表示的区域.
75.函数,的值域为_________.
【答案】
( http: / / www.21cnjy.com )考点:本题主要考查分离变量法求函数的值域,不等式的性质.
76.若关于的不等式的解集为,则实数的取值范围是
【答案】
【解析】
试题分析:当时,恒成立;当时,,故
考点:一元二次不等式的解法
77.若变量、满足约束条件
( http: / / www.21cnjy.com ),则的最大值为
.
【答案】1
【解析】
试题分析:可行域为如图所示三角形内部(包括边界)
( http: / / www.21cnjy.com )
则
考点:线性规划问题
78.设变量满足约束条件
( http: / / www.21cnjy.com )则的取值范围是.
( http: / / www.21cnjy.com )
【答案】
考点:线性规划问题
79.对于实数和,定义运算“”:,设,且关于的方程为恰有三个互不相等的实数根,则的取值范围是___________.
【答案】
【解析】
试题分析:由定义运算“
”可知
( http: / / www.21cnjy.com )
,画出该函数的图像
( http: / / www.21cnjy.com )
如图所示,从而可得,又因为要有三个不同的解,所以,所以,所以的取值范围是.
考点:1.函数的零点;2.新定义新运算;3.基本不等式.
80.若实数满足条件
( http: / / www.21cnjy.com ),则的最大值是________.
【答案】
( http: / / www.21cnjy.com )考点:线性规划.
81.已知,若存在,使得任意恒成立,且两边等号能取到,则的最小值为
.
【答案】
【解析】
试题分析:
,对于任意恒成立,即为函数的最小值,为函数的最大值;若两边等号能取到,则至少为的一个周期,所以最小值为.
考点:三角恒等变换、不等式恒成立问题.
82.已知变量满足约束条件
( http: / / www.21cnjy.com )则的最大值是_________.
【答案】
【解析】可行域表示为三角形及其内部,
因此直线过点时取最大值:
考点:线性规划求范围
83.已知变量满足约束条件
( http: / / www.21cnjy.com )则的取值范围是_________.
【答案】,
( http: / / www.21cnjy.com )考点:线性规划求范围
84.已知正数满足,则的最小值为
.
【答案】9
【解析】
试题分析:因为,当且仅当即时取等号,所以的最小值为9.
考点:基本不等式求最值
85.在平面直角坐标系xOy中,P为不等式组
( http: / / www.21cnjy.com )所表示的平面区域内一动点,则线段|OP|的最小值等于
.
【答案】
【解析】
( http: / / www.21cnjy.com )
考点:线性规划
距离最小
86.不等式解集是_____________________.
【答案】
【解析】
试题分析:设,则
( http: / / www.21cnjy.com ).由,解得,所以解集为
考点:分段函数图像
不等式
87.若实数
( http: / / www.21cnjy.com ),
则目标函数的最大值是
.
【答案】2
( http: / / www.21cnjy.com )考点:线性规划问题。
88.若,则的最小值为
;
【答案】4
【解析】
试题分析:因为所以,当且仅当即时取。
考点:基本不等式。
89.函数y=x+(x≠0)的值域是________.
【答案】(-∞,-4]∪[4,+∞)
【解析】当x>0时,y=x+≥2=4,当x<0时,y=x+=-≤-2=-4.
90.设常数a>0,若9x+≥a+1对一切正实数x成立,则a的取值范围为________.
【答案】
【解析】9x+≥2
=6a,所以6a≥a+1,即a≥
91.不等式组
( http: / / www.21cnjy.com )所表示的平面区域的面积是________.
【答案】25
( http: / / www.21cnjy.com )92.已知一元二次不等式f(x)<0的解集为,则f(10x)>0的解集为______.
【答案】{x|x<-lg2}
【解析】由条件得-1<10x<,即x<-lg2
93.已知函数,且的解集为.
(1)求的值;
(2)若,且,求证:.
【答案】(1)(2)详见解析
【解析】
试题分析:(1)根据绝对值不等式的公式求的解集,因为解集又为,根据对应相等可得的值.(2)由(1)知.根据柯西不等式或基本不等式证明即可.
试题解析:解:(1)因为,
所以等价于,
2分
由有解,得,且其解集为.
4分
又的解集为,故.
(5分)
(2)由(1)知
,又,
7分∴
9分
(或展开运用基本不等式)
∴
.10分
考点:1绝对值不等式;2柯西不等式;3基本不等式.
94.解关于x的不等式:≤
【答案】详见解析
( http: / / www.21cnjy.com )当m>0时,原不等式的解集为
当
1
m=-1时,原不等式的解集为
当m<-1时,原不等式的解集为
考点:1.分式不等式的解法;2.分类讨论思想.
95.已知关于的不等式
的解集为{x∣x<1或x>b}
(1)求的值
(2)解关于的不等式
【答案】(1)
;(2)
(1,2).
【解析】
( http: / / www.21cnjy.com )考点:一元二次不等式的解法.
96.设是定义在上的偶函数,且当时,.若对任意的,不等式恒成立,
求实数的取值范围
【答案】
( http: / / www.21cnjy.com )
若由(2)得成立,则时恒成立,即
,
14分
实数的取值范围
15分
考点:
分段函数,不等式恒成立
97.已知函数
(1)求不等式的解集;
(2)若关于的不等式的解集非空,求实数的取值范围.
【答案】(1);(2)或.
( http: / / www.21cnjy.com )考点:1.绝对值的运算性质;2.绝对值不等式的解法.
98.画出不等式组
( http: / / www.21cnjy.com )表示的平面区域.
【答案】如图
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
99.函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围;
(2)当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
【答案】(1)[-6,2](2)[-7,2]
【解析】(1)∵x∈R,f(x)≥a恒成立,
∴x2+ax+3-a≥0恒成立,则Δ=a2-4(3-a)≤0,得-6≤a≤2.
∴当x∈R时,f(x)≥a恒成立,则a的取值范围为[-6,2].
(2)f(x)=+3-.
讨论对称轴与[-2,2]的位置关系,得到a的取值满足下列条件:
( http: / / www.21cnjy.com )或
( http: / / www.21cnjy.com )或
( http: / / www.21cnjy.com )
即或或
解得-7≤a≤2.∴当x∈[-2,2]时,f(x)≥a恒成立,则a的取值范围为[-7,2].
100.解关于x的不等式(1-ax)2<1.
【答案】当a<0时,原不等式解集为;当a>0时,原不等式解集为
( http: / / www.21cnjy.com )
A(1,1)
B(0,3)
C
x
y
O
