2024-2025学年山东省菏泽市高二下学期教学质量检测数学试题(含答案)
文档属性
| 名称 | 2024-2025学年山东省菏泽市高二下学期教学质量检测数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 151.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 17:51:54 | ||
图片预览



文档简介
2024-2025学年山东省菏泽市高二下学期教学质量检测数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( )
A. B. C. D.
2.两个正态分布和的密度函数图象如图所示,则( )
A. , B. ,
C. , D. ,
3.某质点沿直线运动,位移单位:与时间单位:之间的关系为,则物体在时的瞬时加速度单位:是( )
A. B. C. D.
4.已知函数在上单调递增,则的取值范围是( )
A. B. C. D.
5.假定生男孩和生女孩是等可能的,现随机选择一个有两个小孩的家庭,已知该家庭有女孩,则两个小孩都是女孩的概率是( )
A. B. C. D.
6.已知函数,则的大致图象是( )
A. B. C. D.
7.离散型随机变量的取值为,,,若,,,,则( )
A. B. C. D.
8.用,,组成三位数,数字最多用次,其中,,,则满足条件的三位数个数是( )
A. 个 B. 个 C. 个 D. 个
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知,则( )
A. 的值为
B. 的值为
C. 的值为
D.
10.下列命题正确的有( )
A. 在两个随机变量的线性相关关系中,若相关系数越大,则样本的线性相关性越强
B. 若用不同的模型拟合同一组数据,则残差平方和越小的模型拟合的效果越好
C. 若以模型去拟合某组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,的值分别为,
D. 一组成对数据,,,,,增加一对数据,其中,,线性回归方程不变其中
11.如图,一个质点在随机外力的作用下,从原点出发,每隔向左或向右移动一个单位向左移动的概率为,向右移动的概率为,设移动次后质点位于位置,则下列结论正确的有( )
A. 当,则
B. 当,则
C. 当,该质点共经过两次的概率为
D. 当,的期望
三、填空题:本题共3小题,每小题5分,共15分。
12.在数字通信中,信号是由数字和组成的序列由于随机因素的干扰,发送的信号或有可能被错误地接收为或已知发送信号时,接收为和的概率分别为和发送信号时,接收为和的概率分别为和假设发送信号和是等可能的,则接收信号为的概率是 .
13.把张座位编号为,,,,,的电影票全部分给个人,每人至少分张,至多分张,且这两张票具有连续的编号,那么不同的分法共有 种用数值表示.
14.已知是定义域为的函数,且满足,,则不等式的解集是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知的展开式中第三项的系数是第二项系数的倍.
求的值
求展开式中二项式系数最大的项
求的展开式中含项的系数结果用数值表示.
16.本小题分
为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取名学生通过测试得到了表中数据:
学校 数学成绩 合计
不优秀 优秀
甲校
乙校
合计
依据小概率值的独立性检验,能否据此推断两校学生的数学成绩优秀率有差异如果表中所有数据都扩大为原来的倍,在相同的检验标准下,再用独立性检验推断学校和数学成绩之间的关联性,结论还一样吗请你试着解释其中的原因
现从所抽取的数学成绩优秀学生中利用分层抽样的方法抽取人,再从这人中随机选取人,设这人中来自乙校的人数为,求的分布列和期望.
附:,其中.
临界值表
17.本小题分
已知函数.
若在点处的切线方程为,求的值
求的单调区间.
18.本小题分
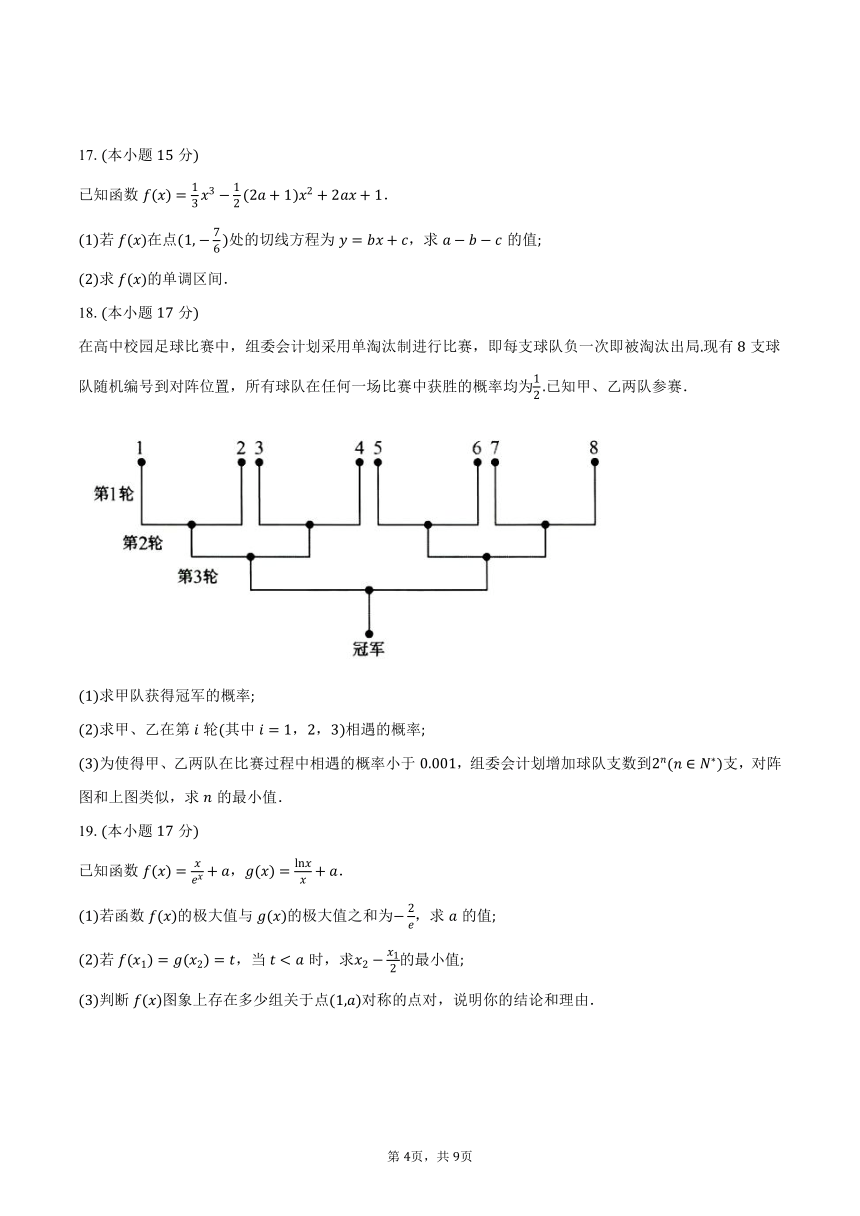
在高中校园足球比赛中,组委会计划采用单淘汰制进行比赛,即每支球队负一次即被淘汰出局现有支球队随机编号到对阵位置,所有球队在任何一场比赛中获胜的概率均为已知甲、乙两队参赛.
求甲队获得冠军的概率
求甲、乙在第轮其中,,相遇的概率
为使得甲、乙两队在比赛过程中相遇的概率小于,组委会计划增加球队支数到支,对阵图和上图类似,求的最小值.
19.本小题分
已知函数,.
若函数的极大值与的极大值之和为,求的值
若,当时,求的最小值
判断图象上存在多少组关于点对称的点对,说明你的结论和理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:的展开式的通项为,
因为第三项的系数是第二项系数的倍,
,解得,
因为,所以;
由知展开式共有项,二项式系数最大的项为第项和第项.
由知第项为,
第项为,
所以二项式系数最大的项为和
由知展开式中的系数为
,
所以展开式中含项的系数为.
16.解:零假设两校学生中数学成绩优秀率之间没有差异.
因为,
依据小概率值的独立性检验,没有充分的理由推断不成立,
所以认为两校学生中数学成绩优秀率之间没有差异,
所有数据都扩大倍后:
,
依据小概率值的独立性检验,可以认为不成立,
即学校与数学成绩有关联,结论不一样,
主要是因为样本容量的不同,导致推断结论发生了变化;
由分层随机抽样可知,抽取的名学生中有名来自乙校,
所有可能的取值为,,,
知,
,
,
所以的分布列为:
故E.
17.解:因为,
所以,
因为过点,
所以,解得,
又因为,在点处的切线方程为,
所以,,
所以
因为,
令,得,,
当即时,
当时,,为增函数
当时,,为减函数
当时,,为增函数
当即时,,在上为增函数
当即时,
当时,,为增函数
当时,,为减函数
当时,,为增函数
综上,当时,的单调递增区间为和,递减区间为
当时,的单调递增区间为,无单调递减区间
当时,的单调递增区间为和,递减区间为.
18.解:设甲队获得冠军为事件,
甲如果想获得冠军,每轮比赛都要获胜,则;
设甲乙第一轮相遇概率为,甲乙第二轮相遇概率为,甲乙第三轮相遇概率为,
设甲的位置固定,若乙要与甲在第一轮相遇只能在同一组,
所以甲乙在第一轮相遇的概率,
甲乙要在第二轮相遇,则甲乙在同一个半区,但不在同一组的概率为,
同时甲乙在第一轮都要获胜则,
甲乙要在第三轮相遇,则甲乙不在同一个半区的概率为,
同时甲乙在第一、二轮都要获胜则;
记比赛的轮次为事件,甲乙在比赛过程中相遇的事件为,
要使甲乙能在第轮相遇,则甲乙必须得在同一个区内的不同半区的概率为,
同时甲乙在前轮都要获胜,
所以
所以甲乙相遇的概率为.,
要使得甲乙相遇的概率小于,
即,即,
又因为为整数,
所以最小的值为.
19.解:因为,所以,
令得,
,,的变化情况列表如下:
单调递增 极大值 单调递减
所以,
因为,所以,
令得,
,,的变化情况列表如下:
单调递增 极大值 单调递减
所以,
所以由已知得,
所以,即.
由题意可知:,
即,
所以,,即且,
又因为,
设,
由知在上单调递增,所以,
,
令,
,
在上,,单调递减,
在上,,单调递增,
所以.
存在唯一的点对关于对称,
证明:假设存在,设,,,
于是得,
即,
令,
,
所以在上单调递减,
,,
由零点存在定理,使得,
即存在唯一的点对,关于对称.
第2页,共2页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( )
A. B. C. D.
2.两个正态分布和的密度函数图象如图所示,则( )
A. , B. ,
C. , D. ,
3.某质点沿直线运动,位移单位:与时间单位:之间的关系为,则物体在时的瞬时加速度单位:是( )
A. B. C. D.
4.已知函数在上单调递增,则的取值范围是( )
A. B. C. D.
5.假定生男孩和生女孩是等可能的,现随机选择一个有两个小孩的家庭,已知该家庭有女孩,则两个小孩都是女孩的概率是( )
A. B. C. D.
6.已知函数,则的大致图象是( )
A. B. C. D.
7.离散型随机变量的取值为,,,若,,,,则( )
A. B. C. D.
8.用,,组成三位数,数字最多用次,其中,,,则满足条件的三位数个数是( )
A. 个 B. 个 C. 个 D. 个
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知,则( )
A. 的值为
B. 的值为
C. 的值为
D.
10.下列命题正确的有( )
A. 在两个随机变量的线性相关关系中,若相关系数越大,则样本的线性相关性越强
B. 若用不同的模型拟合同一组数据,则残差平方和越小的模型拟合的效果越好
C. 若以模型去拟合某组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,的值分别为,
D. 一组成对数据,,,,,增加一对数据,其中,,线性回归方程不变其中
11.如图,一个质点在随机外力的作用下,从原点出发,每隔向左或向右移动一个单位向左移动的概率为,向右移动的概率为,设移动次后质点位于位置,则下列结论正确的有( )
A. 当,则
B. 当,则
C. 当,该质点共经过两次的概率为
D. 当,的期望
三、填空题:本题共3小题,每小题5分,共15分。
12.在数字通信中,信号是由数字和组成的序列由于随机因素的干扰,发送的信号或有可能被错误地接收为或已知发送信号时,接收为和的概率分别为和发送信号时,接收为和的概率分别为和假设发送信号和是等可能的,则接收信号为的概率是 .
13.把张座位编号为,,,,,的电影票全部分给个人,每人至少分张,至多分张,且这两张票具有连续的编号,那么不同的分法共有 种用数值表示.
14.已知是定义域为的函数,且满足,,则不等式的解集是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知的展开式中第三项的系数是第二项系数的倍.
求的值
求展开式中二项式系数最大的项
求的展开式中含项的系数结果用数值表示.
16.本小题分
为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取名学生通过测试得到了表中数据:
学校 数学成绩 合计
不优秀 优秀
甲校
乙校
合计
依据小概率值的独立性检验,能否据此推断两校学生的数学成绩优秀率有差异如果表中所有数据都扩大为原来的倍,在相同的检验标准下,再用独立性检验推断学校和数学成绩之间的关联性,结论还一样吗请你试着解释其中的原因
现从所抽取的数学成绩优秀学生中利用分层抽样的方法抽取人,再从这人中随机选取人,设这人中来自乙校的人数为,求的分布列和期望.
附:,其中.
临界值表
17.本小题分
已知函数.
若在点处的切线方程为,求的值
求的单调区间.
18.本小题分
在高中校园足球比赛中,组委会计划采用单淘汰制进行比赛,即每支球队负一次即被淘汰出局现有支球队随机编号到对阵位置,所有球队在任何一场比赛中获胜的概率均为已知甲、乙两队参赛.
求甲队获得冠军的概率
求甲、乙在第轮其中,,相遇的概率
为使得甲、乙两队在比赛过程中相遇的概率小于,组委会计划增加球队支数到支,对阵图和上图类似,求的最小值.
19.本小题分
已知函数,.
若函数的极大值与的极大值之和为,求的值
若,当时,求的最小值
判断图象上存在多少组关于点对称的点对,说明你的结论和理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:的展开式的通项为,
因为第三项的系数是第二项系数的倍,
,解得,
因为,所以;
由知展开式共有项,二项式系数最大的项为第项和第项.
由知第项为,
第项为,
所以二项式系数最大的项为和
由知展开式中的系数为
,
所以展开式中含项的系数为.
16.解:零假设两校学生中数学成绩优秀率之间没有差异.
因为,
依据小概率值的独立性检验,没有充分的理由推断不成立,
所以认为两校学生中数学成绩优秀率之间没有差异,
所有数据都扩大倍后:
,
依据小概率值的独立性检验,可以认为不成立,
即学校与数学成绩有关联,结论不一样,
主要是因为样本容量的不同,导致推断结论发生了变化;
由分层随机抽样可知,抽取的名学生中有名来自乙校,
所有可能的取值为,,,
知,
,
,
所以的分布列为:
故E.
17.解:因为,
所以,
因为过点,
所以,解得,
又因为,在点处的切线方程为,
所以,,
所以
因为,
令,得,,
当即时,
当时,,为增函数
当时,,为减函数
当时,,为增函数
当即时,,在上为增函数
当即时,
当时,,为增函数
当时,,为减函数
当时,,为增函数
综上,当时,的单调递增区间为和,递减区间为
当时,的单调递增区间为,无单调递减区间
当时,的单调递增区间为和,递减区间为.
18.解:设甲队获得冠军为事件,
甲如果想获得冠军,每轮比赛都要获胜,则;
设甲乙第一轮相遇概率为,甲乙第二轮相遇概率为,甲乙第三轮相遇概率为,
设甲的位置固定,若乙要与甲在第一轮相遇只能在同一组,
所以甲乙在第一轮相遇的概率,
甲乙要在第二轮相遇,则甲乙在同一个半区,但不在同一组的概率为,
同时甲乙在第一轮都要获胜则,
甲乙要在第三轮相遇,则甲乙不在同一个半区的概率为,
同时甲乙在第一、二轮都要获胜则;
记比赛的轮次为事件,甲乙在比赛过程中相遇的事件为,
要使甲乙能在第轮相遇,则甲乙必须得在同一个区内的不同半区的概率为,
同时甲乙在前轮都要获胜,
所以
所以甲乙相遇的概率为.,
要使得甲乙相遇的概率小于,
即,即,
又因为为整数,
所以最小的值为.
19.解:因为,所以,
令得,
,,的变化情况列表如下:
单调递增 极大值 单调递减
所以,
因为,所以,
令得,
,,的变化情况列表如下:
单调递增 极大值 单调递减
所以,
所以由已知得,
所以,即.
由题意可知:,
即,
所以,,即且,
又因为,
设,
由知在上单调递增,所以,
,
令,
,
在上,,单调递减,
在上,,单调递增,
所以.
存在唯一的点对关于对称,
证明:假设存在,设,,,
于是得,
即,
令,
,
所以在上单调递减,
,,
由零点存在定理,使得,
即存在唯一的点对,关于对称.
第2页,共2页
同课章节目录
