浙江省绍兴市2024-2025学年八年级下学期期中数学试卷(含答案)
文档属性
| 名称 | 浙江省绍兴市2024-2025学年八年级下学期期中数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 753.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 21:56:25 | ||
图片预览



文档简介
2024-2025学年浙江省绍兴八年级下期中数学试卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)剪纸艺术是国家级第一批非物质文化遗产,下列图案中,既是中心对称又是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)甲、乙两台机床同时生产直径为10mm的零件,为了检验产品的质量,质检人员从两台机床生产的产品中各抽出5件进行测量,测量结果(单位:mm)如表.
机床甲 10 9.9 10 10.2 9.9
机床乙 10.1 10 9.9 10 10
这两组数据的平均数分别为( )
A.9.9,10 B.10,10 C.9.9,10.1 D.10.1,10
3.(3分)下列关于二次根式的计算正确的是( )
A. B.
C. D.
4.(3分)为调动学生参与体育锻炼的积极性,某校组织一分钟跳绳比赛活动.体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成如下统计表:
一分钟跳绳个数(个) 141 144 145 146
学生人数(名) 5 2 1 2
这组数据的中位数和众数分别是( )
A.144,141 B.142.5,5 C.144.5,141 D.142.5,141
5.(3分)用反证法证明“在△ABC中,若∠B≠∠C,则AB≠AC”时,我们应该先假设( )
A.∠B=∠C B.∠A=∠B C.AB=AC D.AC=BC
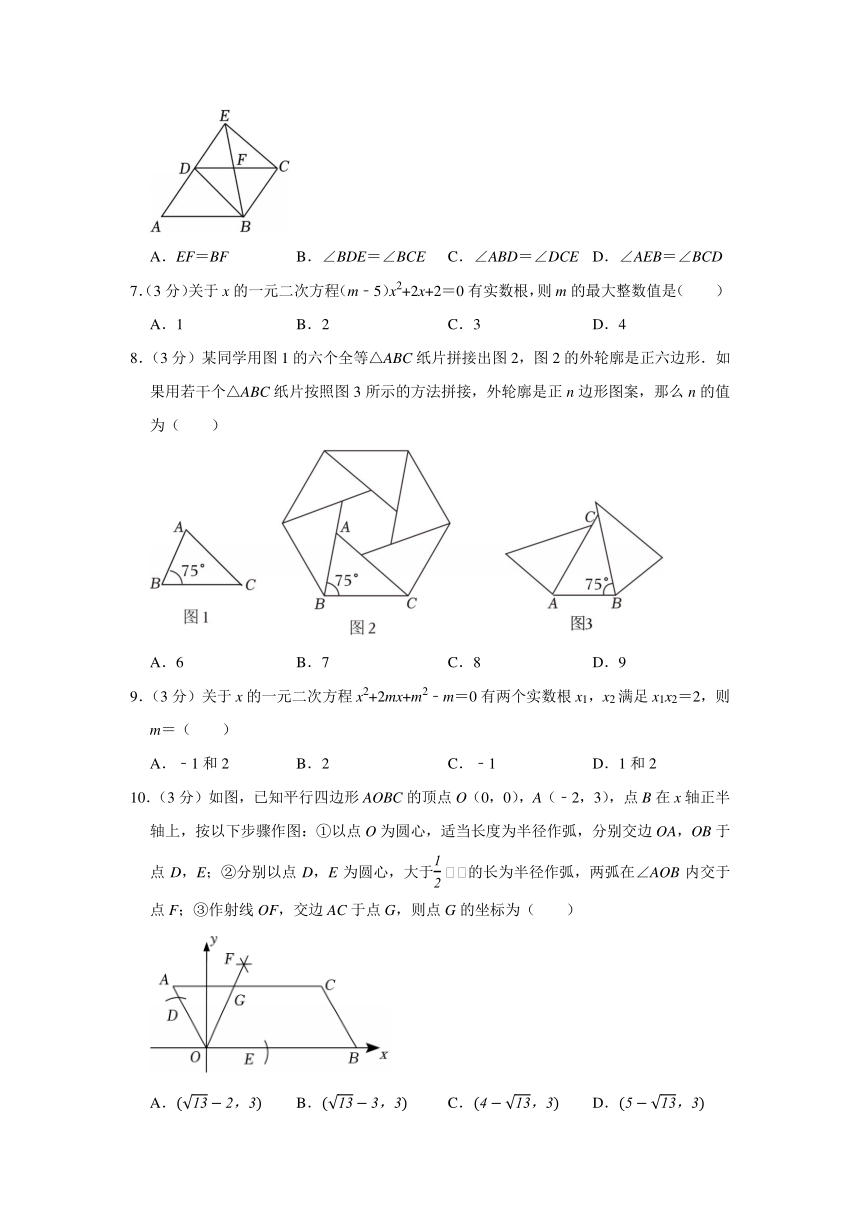
6.(3分)如图,E是 ABCD的边AD延长线上一点,连接BE,CE,BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.EF=BF B.∠BDE=∠BCE C.∠ABD=∠DCE D.∠AEB=∠BCD
7.(3分)关于x的一元二次方程(m﹣5)x2+2x+2=0有实数根,则m的最大整数值是( )
A.1 B.2 C.3 D.4
8.(3分)某同学用图1的六个全等△ABC纸片拼接出图2,图2的外轮廓是正六边形.如果用若干个△ABC纸片按照图3所示的方法拼接,外轮廓是正n边形图案,那么n的值为( )
A.6 B.7 C.8 D.9
9.(3分)关于x的一元二次方程x2+2mx+m2﹣m=0有两个实数根x1,x2满足x1x2=2,则m=( )
A.﹣1和2 B.2 C.﹣1 D.1和2
10.(3分)如图,已知平行四边形AOBC的顶点O(0,0),A(﹣2,3),点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A. B. C. D.
二.填空题(共10小题,满分30分,每小题3分)
11.(3分)计算:当x 时,有意义.
12.(3分)计算: ;(3) .
13.(3分)学校举行投篮比赛,某班有8名同学参加了比赛,比赛结束后,老师统计了他们各自的投篮数,分别为3,5,5,6,5,6,4,6.则这组数据的方差为 .
14.(3分)若一个正多边形的每一个内角都比它相邻外角的3倍还多20°,则这个正多边形的边数为 .
15.(3分)若,则x2﹣2x+4的值是 .
16.(3分)若x=﹣1是关于x的方程ax2+bx﹣2=0的一个解,则代数式2024+a﹣b的值为 .
17.(3分)如图,在△ABC中,CD⊥AB于点D,E,F分别为AC,BC的中点.AB=10,BC=8,DE=4.6,则△DEF的周长是 .
18.(3分)已知矩形的周长为14,面积为12,则它的对角线长为 .
19.(3分)请写出一个关于x的一元二次方程,使该方程有一个正根和一个负根,那么这个方程可以是 .
20.(3分)如图,在四边形ABCD中,AB=12,CD=10,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,则EF的长为 .
三.解答题(共6小题,满分40分)
21.(6分)计算:
(1).
(2).
22.(6分)解方程:
(1)(x+2)2=4(x+2);
(2)2x2﹣3x﹣1=0.
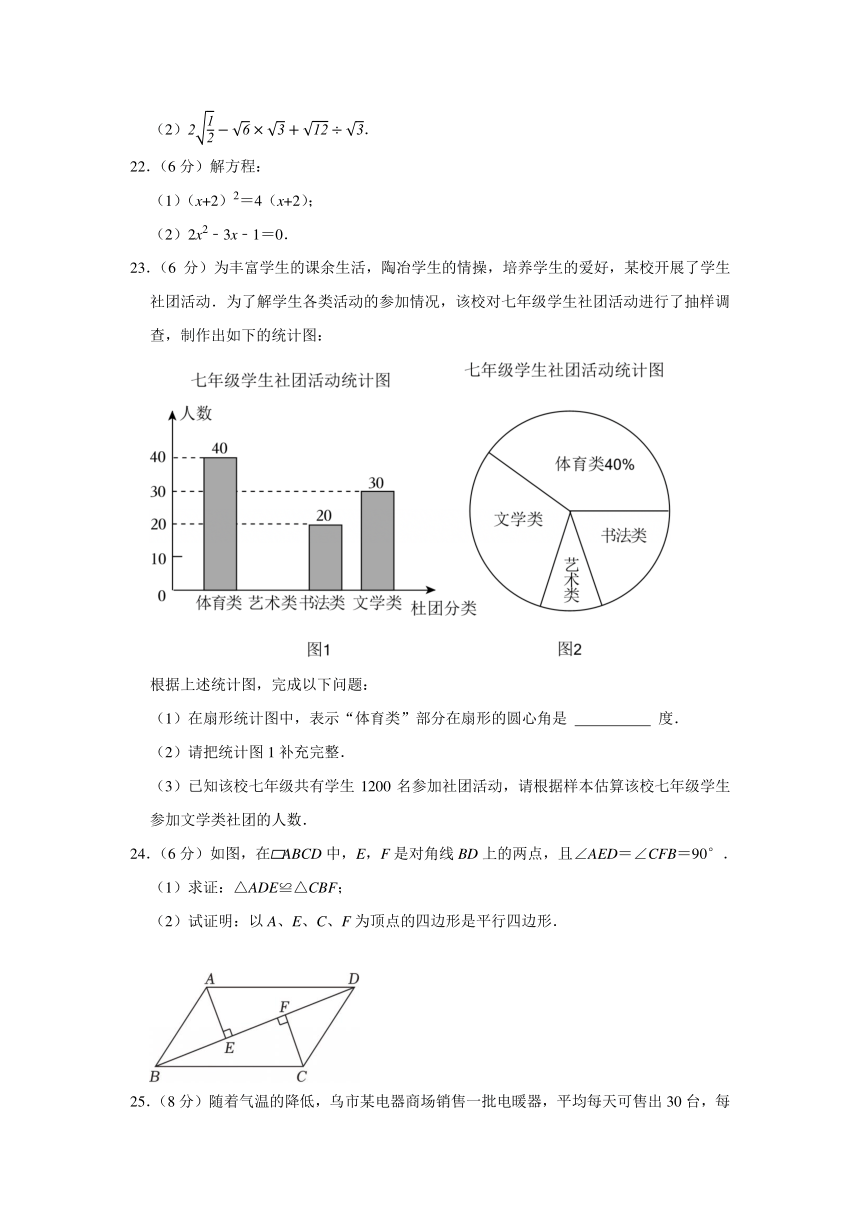
23.(6分)为丰富学生的课余生活,陶冶学生的情操,培养学生的爱好,某校开展了学生社团活动.为了解学生各类活动的参加情况,该校对七年级学生社团活动进行了抽样调查,制作出如下的统计图:
根据上述统计图,完成以下问题:
(1)在扇形统计图中,表示“体育类”部分在扇形的圆心角是 度.
(2)请把统计图1补充完整.
(3)已知该校七年级共有学生1200名参加社团活动,请根据样本估算该校七年级学生参加文学类社团的人数.
24.(6分)如图,在 ABCD中,E,F是对角线BD上的两点,且∠AED=∠CFB=90°.
(1)求证:△ADE≌△CBF;
(2)试证明:以A、E、C、F为顶点的四边形是平行四边形.
25.(8分)随着气温的降低,乌市某电器商场销售一批电暖器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台每降价1元,商场平均每天可多售出2台.设每台降价x元,则:
(1)每天可销售 台,每台盈利 元;(用含x的式子表示)
(2)在尽快减少库存的前提下,商场每天要盈利2100元,每台电暖器应降价多少元?
(3)该商场平均每天盈利能达到2500元吗?如果能,求出此时应降价多少;如果不能,请说明理由.
26.(8分)如图所示,在四边形ABCD中,AD∥BC,AD=27cm,BC=36cm,点P从A向终点D以1cm/s的速度运动.点Q从点C向终点B以2cm/s的速度运动.P,Q两点同时出发,有一点到达终点停止后另一点也停止运动,直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD.
(1)当运动t秒时,线段PD= cm,BQ= cm(用含有t的代数式表示);
(2)直线PQ运动多少秒后将四边形ABCD截得两个四边形中一个四边形为平行四边形?
(3)直线PQ运动多少秒后将四边形ABCD截得两个面积相等的四边形?
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B D C D D C B A
二.填空题(共10小题,满分30分,每小题3分)
11.(3分)计算:当x 时,有意义.
12.(3分)计算: ;(3) .
13.(3分)学校举行投篮比赛,某班有8名同学参加了比赛,比赛结束后,老师统计了他们各自的投篮数,分别为3,5,5,6,5,6,4,6.则这组数据的方差为 1 .
14.(3分)若一个正多边形的每一个内角都比它相邻外角的3倍还多20°,则这个正多边形的边数为 9 .
15.(3分)若,则x2﹣2x+4的值是 5 .
16.(3分)若x=﹣1是关于x的方程ax2+bx﹣2=0的一个解,则代数式2024+a﹣b的值为 2026 .
17.(3分)如图,在△ABC中,CD⊥AB于点D,E,F分别为AC,BC的中点.AB=10,BC=8,DE=4.6,则△DEF的周长是 13.6 .
18.(3分)已知矩形的周长为14,面积为12,则它的对角线长为 5 .
19.(3分)请写出一个关于x的一元二次方程,使该方程有一个正根和一个负根,那么这个方程可以是 x2﹣1=0(答案不唯一) .
20.(3分)如图,在四边形ABCD中,AB=12,CD=10,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,则EF的长为 .
三.解答题(共6小题,满分40分)
21.(6分)计算:
(1).
(2).
【解答】解:(1)原式=3﹣5+2=0;
(2)原式
.
22.(6分)解方程:
(1)(x+2)2=4(x+2);
(2)2x2﹣3x﹣1=0.
【解答】解:(1)∵(x+2)2=4(x+2),
∴(x+2)2﹣4(x+2)=0,
则(x+2)(x﹣2)=0,
∴x+2=0或x﹣2=0,
解得x1=﹣2,x2=2;
(2)∵a=2,b=﹣3,c=﹣1,
∴Δ=(﹣3)2﹣4×2×(﹣1)=17>0,
∴x,
即x1,x2.
23.(6分)为丰富学生的课余生活,陶冶学生的情操,培养学生的爱好,某校开展了学生社团活动.为了解学生各类活动的参加情况,该校对七年级学生社团活动进行了抽样调查,制作出如下的统计图:
根据上述统计图,完成以下问题:
(1)在扇形统计图中,表示“体育类”部分在扇形的圆心角是 144 度.
(2)请把统计图1补充完整.
(3)已知该校七年级共有学生1200名参加社团活动,请根据样本估算该校七年级学生参加文学类社团的人数.
【解答】解:(1)在扇形统计图中,表示“体育类”部分在扇形的圆心角是360°×40%=144°;
故答案为:144;
(2)这次共调查了40÷40%=100(名),
艺术的人数为100﹣(40+20+30)=10(名),
补全条形统计图:
(3)1200360(人),
答:该校七年级学生参加文学类社团的人数约为360人.
24.(6分)如图,在 ABCD中,E,F是对角线BD上的两点,且∠AED=∠CFB=90°.
(1)求证:△ADE≌△CBF;
(2)试证明:以A、E、C、F为顶点的四边形是平行四边形.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS);
(2)∵∠AED=∠CFB=90°,
∴AE∥CF,
由(1)可知,△ADE≌△CBF,
∴AE=CF,
∴以A、E、C、F为顶点的四边形是平行四边形.
25.(8分)随着气温的降低,乌市某电器商场销售一批电暖器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台每降价1元,商场平均每天可多售出2台.设每台降价x元,则:
(1)每天可销售 (30+2x) 台,每台盈利 (50﹣x) 元;(用含x的式子表示)
(2)在尽快减少库存的前提下,商场每天要盈利2100元,每台电暖器应降价多少元?
(3)该商场平均每天盈利能达到2500元吗?如果能,求出此时应降价多少;如果不能,请说明理由.
【解答】解:(1)设每台空气加湿器降价x元,则每天盈利(50﹣x)元,每天可以售出(30+2x)台,
故答案为:(30+2x);(50﹣x),
(2)设每台空气加湿器降价x元,则每天盈利(50﹣x)元,每天可以售出(30+2x)台,
依题意得:(50﹣x)(30+2x)=2100,
整理得:x2﹣35x+300=0,
解得:x1=15,x2=20.
又∵要尽快减少库存,
∴x=20.
答:每台空气加湿器应降价20元.
(3)不能,理由如下:
设每台空气加湿器降价x元,则每天盈利(50﹣x)元,每天可以售出(30+2x)台,
依题意得:(50﹣x)(30+2x)=2500,
整理得:x2﹣35x+500=0.
∵Δ=(﹣35)2﹣4×1×500=﹣775<0,
∴该方程无实数根,
∴该商场平均每天盈利不能达到2500元.
26.(8分)如图所示,在四边形ABCD中,AD∥BC,AD=27cm,BC=36cm,点P从A向终点D以1cm/s的速度运动.点Q从点C向终点B以2cm/s的速度运动.P,Q两点同时出发,有一点到达终点停止后另一点也停止运动,直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD.
(1)当运动t秒时,线段PD= (27﹣t) cm,BQ= (36﹣2t) cm(用含有t的代数式表示);
(2)直线PQ运动多少秒后将四边形ABCD截得两个四边形中一个四边形为平行四边形?
(3)直线PQ运动多少秒后将四边形ABCD截得两个面积相等的四边形?
【解答】解:(1)根据题意得:当运动t秒时,线段AP=t cm,CQ=2t cm,PD=AD﹣AP=(27﹣t)cm,BQ=BC﹣CQ=(36﹣2t)cm.
故答案为:(27﹣t),(36﹣2t);
(2)∵AD∥BC,
∴当AP=BQ或PD=CQ时,PQ将四边形ABCD截得两个四边形中一个四边形为平行四边形.
当AP=BQ时,t=36﹣2t,
解得:t=12;
当PD=CQ时,27﹣t=2t,
解得:t=9.
答:直线PQ运动9或12秒后,将四边形ABCD截得两个四边形中一个四边形为平行四边形;
(3)根据题意得:AP+BQ=PD+CQ,
即t+36﹣2t=27﹣t+2t,
解得:t.
答:直线PQ运动秒后,将四边形ABCD截得两个面积相等的四边形.
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)剪纸艺术是国家级第一批非物质文化遗产,下列图案中,既是中心对称又是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)甲、乙两台机床同时生产直径为10mm的零件,为了检验产品的质量,质检人员从两台机床生产的产品中各抽出5件进行测量,测量结果(单位:mm)如表.
机床甲 10 9.9 10 10.2 9.9
机床乙 10.1 10 9.9 10 10
这两组数据的平均数分别为( )
A.9.9,10 B.10,10 C.9.9,10.1 D.10.1,10
3.(3分)下列关于二次根式的计算正确的是( )
A. B.
C. D.
4.(3分)为调动学生参与体育锻炼的积极性,某校组织一分钟跳绳比赛活动.体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成如下统计表:
一分钟跳绳个数(个) 141 144 145 146
学生人数(名) 5 2 1 2
这组数据的中位数和众数分别是( )
A.144,141 B.142.5,5 C.144.5,141 D.142.5,141
5.(3分)用反证法证明“在△ABC中,若∠B≠∠C,则AB≠AC”时,我们应该先假设( )
A.∠B=∠C B.∠A=∠B C.AB=AC D.AC=BC
6.(3分)如图,E是 ABCD的边AD延长线上一点,连接BE,CE,BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( )
A.EF=BF B.∠BDE=∠BCE C.∠ABD=∠DCE D.∠AEB=∠BCD
7.(3分)关于x的一元二次方程(m﹣5)x2+2x+2=0有实数根,则m的最大整数值是( )
A.1 B.2 C.3 D.4
8.(3分)某同学用图1的六个全等△ABC纸片拼接出图2,图2的外轮廓是正六边形.如果用若干个△ABC纸片按照图3所示的方法拼接,外轮廓是正n边形图案,那么n的值为( )
A.6 B.7 C.8 D.9
9.(3分)关于x的一元二次方程x2+2mx+m2﹣m=0有两个实数根x1,x2满足x1x2=2,则m=( )
A.﹣1和2 B.2 C.﹣1 D.1和2
10.(3分)如图,已知平行四边形AOBC的顶点O(0,0),A(﹣2,3),点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A. B. C. D.
二.填空题(共10小题,满分30分,每小题3分)
11.(3分)计算:当x 时,有意义.
12.(3分)计算: ;(3) .
13.(3分)学校举行投篮比赛,某班有8名同学参加了比赛,比赛结束后,老师统计了他们各自的投篮数,分别为3,5,5,6,5,6,4,6.则这组数据的方差为 .
14.(3分)若一个正多边形的每一个内角都比它相邻外角的3倍还多20°,则这个正多边形的边数为 .
15.(3分)若,则x2﹣2x+4的值是 .
16.(3分)若x=﹣1是关于x的方程ax2+bx﹣2=0的一个解,则代数式2024+a﹣b的值为 .
17.(3分)如图,在△ABC中,CD⊥AB于点D,E,F分别为AC,BC的中点.AB=10,BC=8,DE=4.6,则△DEF的周长是 .
18.(3分)已知矩形的周长为14,面积为12,则它的对角线长为 .
19.(3分)请写出一个关于x的一元二次方程,使该方程有一个正根和一个负根,那么这个方程可以是 .
20.(3分)如图,在四边形ABCD中,AB=12,CD=10,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,则EF的长为 .
三.解答题(共6小题,满分40分)
21.(6分)计算:
(1).
(2).
22.(6分)解方程:
(1)(x+2)2=4(x+2);
(2)2x2﹣3x﹣1=0.
23.(6分)为丰富学生的课余生活,陶冶学生的情操,培养学生的爱好,某校开展了学生社团活动.为了解学生各类活动的参加情况,该校对七年级学生社团活动进行了抽样调查,制作出如下的统计图:
根据上述统计图,完成以下问题:
(1)在扇形统计图中,表示“体育类”部分在扇形的圆心角是 度.
(2)请把统计图1补充完整.
(3)已知该校七年级共有学生1200名参加社团活动,请根据样本估算该校七年级学生参加文学类社团的人数.
24.(6分)如图,在 ABCD中,E,F是对角线BD上的两点,且∠AED=∠CFB=90°.
(1)求证:△ADE≌△CBF;
(2)试证明:以A、E、C、F为顶点的四边形是平行四边形.
25.(8分)随着气温的降低,乌市某电器商场销售一批电暖器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台每降价1元,商场平均每天可多售出2台.设每台降价x元,则:
(1)每天可销售 台,每台盈利 元;(用含x的式子表示)
(2)在尽快减少库存的前提下,商场每天要盈利2100元,每台电暖器应降价多少元?
(3)该商场平均每天盈利能达到2500元吗?如果能,求出此时应降价多少;如果不能,请说明理由.
26.(8分)如图所示,在四边形ABCD中,AD∥BC,AD=27cm,BC=36cm,点P从A向终点D以1cm/s的速度运动.点Q从点C向终点B以2cm/s的速度运动.P,Q两点同时出发,有一点到达终点停止后另一点也停止运动,直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD.
(1)当运动t秒时,线段PD= cm,BQ= cm(用含有t的代数式表示);
(2)直线PQ运动多少秒后将四边形ABCD截得两个四边形中一个四边形为平行四边形?
(3)直线PQ运动多少秒后将四边形ABCD截得两个面积相等的四边形?
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B D C D D C B A
二.填空题(共10小题,满分30分,每小题3分)
11.(3分)计算:当x 时,有意义.
12.(3分)计算: ;(3) .
13.(3分)学校举行投篮比赛,某班有8名同学参加了比赛,比赛结束后,老师统计了他们各自的投篮数,分别为3,5,5,6,5,6,4,6.则这组数据的方差为 1 .
14.(3分)若一个正多边形的每一个内角都比它相邻外角的3倍还多20°,则这个正多边形的边数为 9 .
15.(3分)若,则x2﹣2x+4的值是 5 .
16.(3分)若x=﹣1是关于x的方程ax2+bx﹣2=0的一个解,则代数式2024+a﹣b的值为 2026 .
17.(3分)如图,在△ABC中,CD⊥AB于点D,E,F分别为AC,BC的中点.AB=10,BC=8,DE=4.6,则△DEF的周长是 13.6 .
18.(3分)已知矩形的周长为14,面积为12,则它的对角线长为 5 .
19.(3分)请写出一个关于x的一元二次方程,使该方程有一个正根和一个负根,那么这个方程可以是 x2﹣1=0(答案不唯一) .
20.(3分)如图,在四边形ABCD中,AB=12,CD=10,∠ABD=30°,∠BDC=120°,E,F分别是AD,BC的中点,则EF的长为 .
三.解答题(共6小题,满分40分)
21.(6分)计算:
(1).
(2).
【解答】解:(1)原式=3﹣5+2=0;
(2)原式
.
22.(6分)解方程:
(1)(x+2)2=4(x+2);
(2)2x2﹣3x﹣1=0.
【解答】解:(1)∵(x+2)2=4(x+2),
∴(x+2)2﹣4(x+2)=0,
则(x+2)(x﹣2)=0,
∴x+2=0或x﹣2=0,
解得x1=﹣2,x2=2;
(2)∵a=2,b=﹣3,c=﹣1,
∴Δ=(﹣3)2﹣4×2×(﹣1)=17>0,
∴x,
即x1,x2.
23.(6分)为丰富学生的课余生活,陶冶学生的情操,培养学生的爱好,某校开展了学生社团活动.为了解学生各类活动的参加情况,该校对七年级学生社团活动进行了抽样调查,制作出如下的统计图:
根据上述统计图,完成以下问题:
(1)在扇形统计图中,表示“体育类”部分在扇形的圆心角是 144 度.
(2)请把统计图1补充完整.
(3)已知该校七年级共有学生1200名参加社团活动,请根据样本估算该校七年级学生参加文学类社团的人数.
【解答】解:(1)在扇形统计图中,表示“体育类”部分在扇形的圆心角是360°×40%=144°;
故答案为:144;
(2)这次共调查了40÷40%=100(名),
艺术的人数为100﹣(40+20+30)=10(名),
补全条形统计图:
(3)1200360(人),
答:该校七年级学生参加文学类社团的人数约为360人.
24.(6分)如图,在 ABCD中,E,F是对角线BD上的两点,且∠AED=∠CFB=90°.
(1)求证:△ADE≌△CBF;
(2)试证明:以A、E、C、F为顶点的四边形是平行四边形.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,
∴∠ADE=∠CBF,
∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS);
(2)∵∠AED=∠CFB=90°,
∴AE∥CF,
由(1)可知,△ADE≌△CBF,
∴AE=CF,
∴以A、E、C、F为顶点的四边形是平行四边形.
25.(8分)随着气温的降低,乌市某电器商场销售一批电暖器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台每降价1元,商场平均每天可多售出2台.设每台降价x元,则:
(1)每天可销售 (30+2x) 台,每台盈利 (50﹣x) 元;(用含x的式子表示)
(2)在尽快减少库存的前提下,商场每天要盈利2100元,每台电暖器应降价多少元?
(3)该商场平均每天盈利能达到2500元吗?如果能,求出此时应降价多少;如果不能,请说明理由.
【解答】解:(1)设每台空气加湿器降价x元,则每天盈利(50﹣x)元,每天可以售出(30+2x)台,
故答案为:(30+2x);(50﹣x),
(2)设每台空气加湿器降价x元,则每天盈利(50﹣x)元,每天可以售出(30+2x)台,
依题意得:(50﹣x)(30+2x)=2100,
整理得:x2﹣35x+300=0,
解得:x1=15,x2=20.
又∵要尽快减少库存,
∴x=20.
答:每台空气加湿器应降价20元.
(3)不能,理由如下:
设每台空气加湿器降价x元,则每天盈利(50﹣x)元,每天可以售出(30+2x)台,
依题意得:(50﹣x)(30+2x)=2500,
整理得:x2﹣35x+500=0.
∵Δ=(﹣35)2﹣4×1×500=﹣775<0,
∴该方程无实数根,
∴该商场平均每天盈利不能达到2500元.
26.(8分)如图所示,在四边形ABCD中,AD∥BC,AD=27cm,BC=36cm,点P从A向终点D以1cm/s的速度运动.点Q从点C向终点B以2cm/s的速度运动.P,Q两点同时出发,有一点到达终点停止后另一点也停止运动,直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD.
(1)当运动t秒时,线段PD= (27﹣t) cm,BQ= (36﹣2t) cm(用含有t的代数式表示);
(2)直线PQ运动多少秒后将四边形ABCD截得两个四边形中一个四边形为平行四边形?
(3)直线PQ运动多少秒后将四边形ABCD截得两个面积相等的四边形?
【解答】解:(1)根据题意得:当运动t秒时,线段AP=t cm,CQ=2t cm,PD=AD﹣AP=(27﹣t)cm,BQ=BC﹣CQ=(36﹣2t)cm.
故答案为:(27﹣t),(36﹣2t);
(2)∵AD∥BC,
∴当AP=BQ或PD=CQ时,PQ将四边形ABCD截得两个四边形中一个四边形为平行四边形.
当AP=BQ时,t=36﹣2t,
解得:t=12;
当PD=CQ时,27﹣t=2t,
解得:t=9.
答:直线PQ运动9或12秒后,将四边形ABCD截得两个四边形中一个四边形为平行四边形;
(3)根据题意得:AP+BQ=PD+CQ,
即t+36﹣2t=27﹣t+2t,
解得:t.
答:直线PQ运动秒后,将四边形ABCD截得两个面积相等的四边形.
同课章节目录
