1.3 反比例函数的应用 同步练习(含答案)
文档属性
| 名称 | 1.3 反比例函数的应用 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
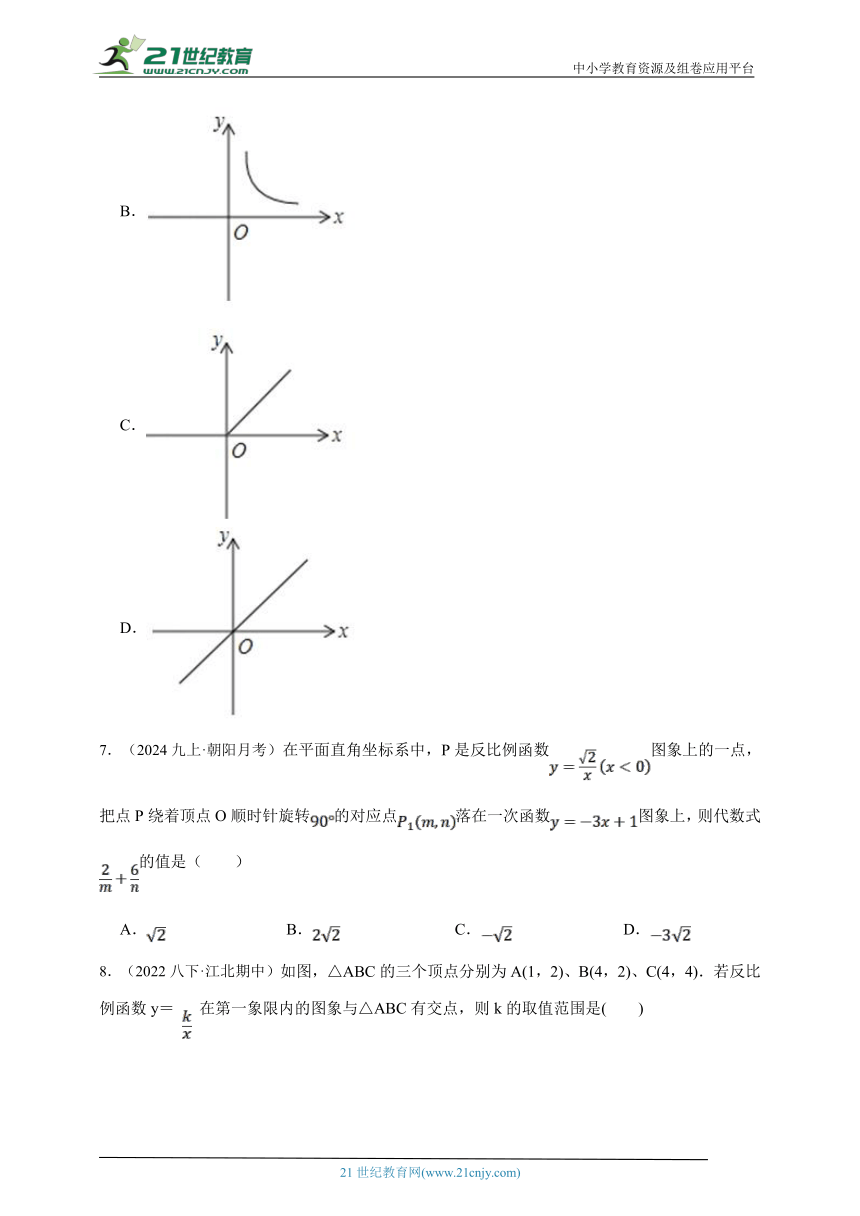
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 21:21:09 | ||
图片预览


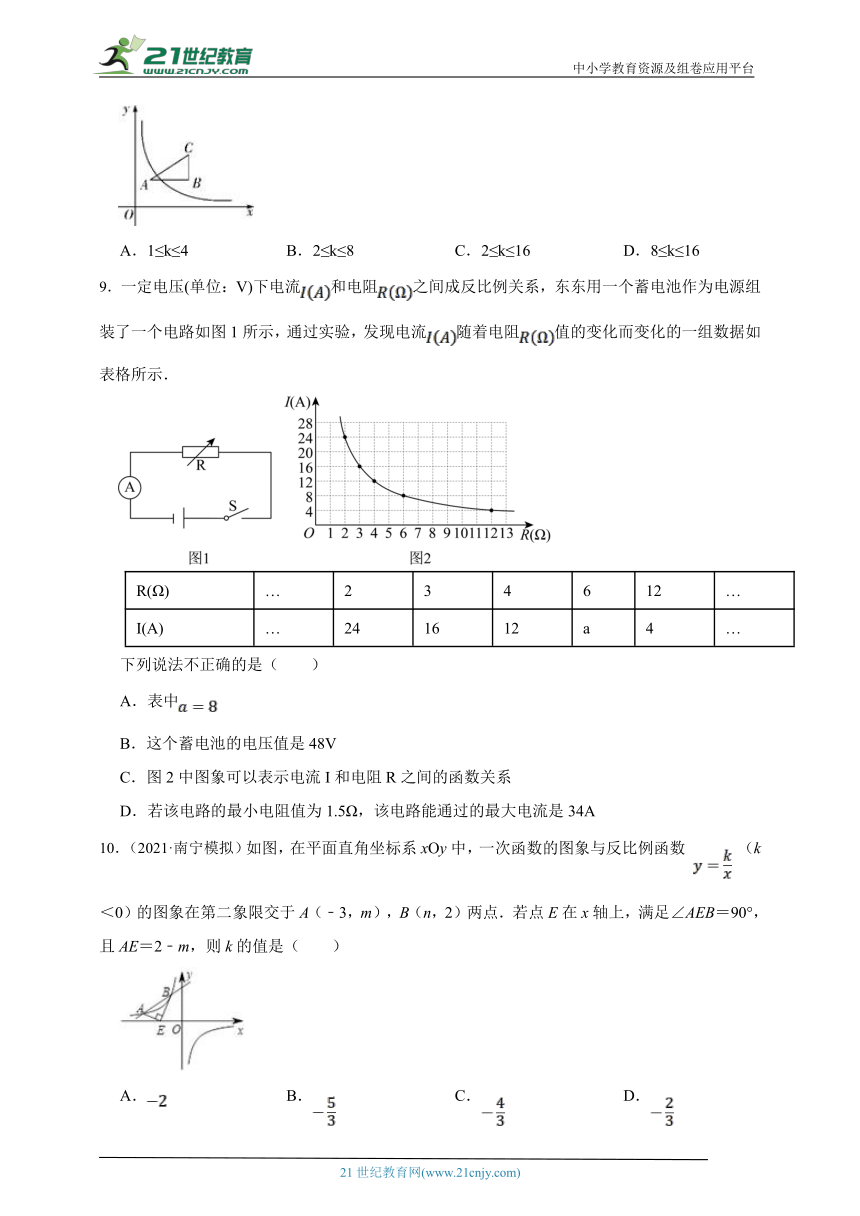
文档简介
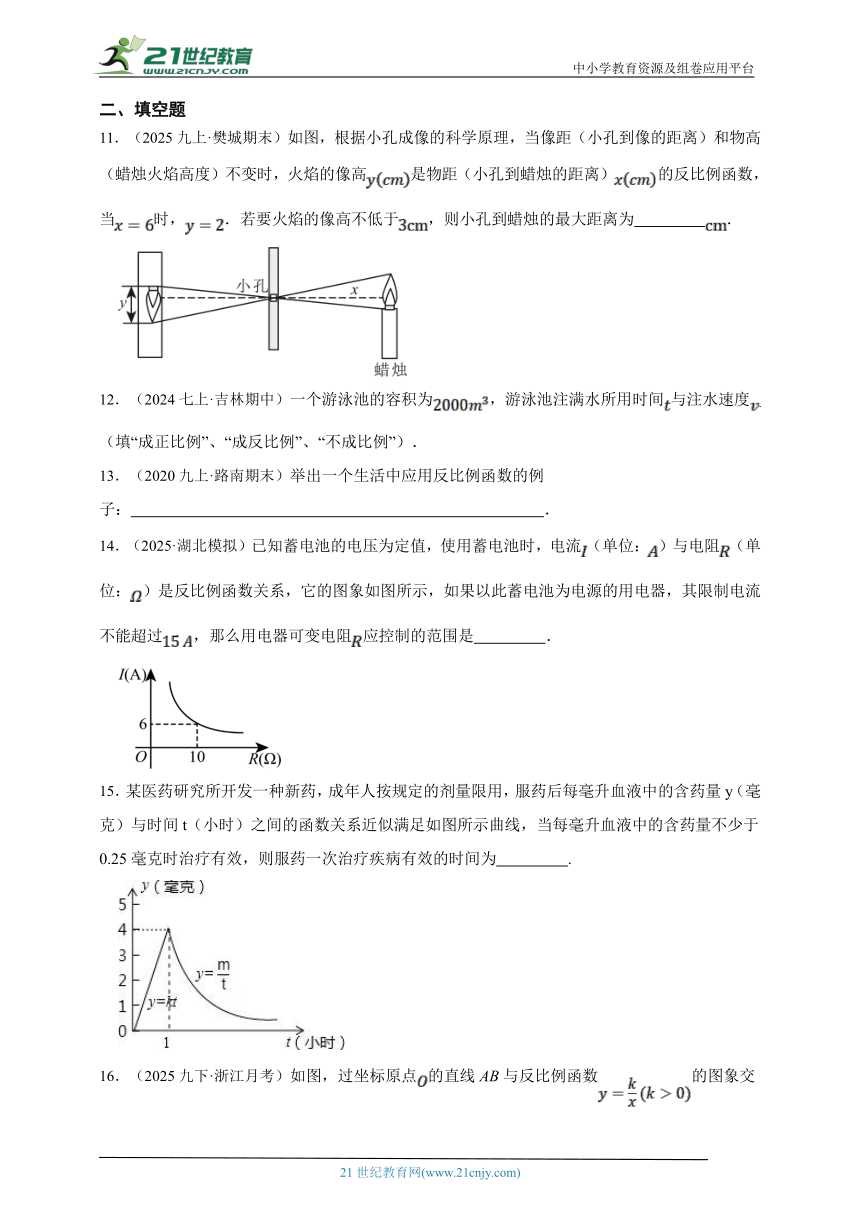
中小学教育资源及组卷应用平台
1.3 反比例函数的应用
一、单选题
1.(2023九下·蔚县模拟)如图1,某长方体A,B,C三个面的面积之比是,当A,B,C三个面分别接触地面时,水平地面所受压强分别为,,.已知满足的函数图象,如图2所示,其中p是压强,F是压力(物体放在水平地面上,物体对地面的压力等于该物体的重力),S是受力面积,则,,的大小关系为( )
A. B. C. D.
2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
A. B. C. D.
3.(2024九上·七里河期末)我们知道压强p,是指物体单位面积S上受到的压力F,即.如果的压力F作用于物体上,产生的压强p要大于,则下列关于物体受力面积的说法正确的是( )
A.S小于 B.S大于 C.S小于 D.S大于
4.(2023九下·裕华模拟)已知闭合电路的电压为定值,电流()与电路的电阻()是反比例函数关系,根据下表判断以下选项正确的是( )
()
()
A.与的关系式为 B.
C. D.当时,
5.(2024九下·石家庄模拟)已知通过电阻R的电流I和电阻两端电压满足关系式,如图所示的四个点分别描述甲、乙、丙、丁四个电阻在不同电路中通过电阻的电流与该电阻阻值的情况,其中描述甲、丙两个电阻的情况点恰好在同一个反比例函数的图象上,则这四个电阻两端的电压最小的是( )
A.甲 B.乙 C.丙 D.丁.
6.小明乘车从广州到北京,行车的平均速度y(km/h)和行车时间x(h)之间的函数图象( )
A.
B.
C.
D.
7.(2024九上·朝阳月考)在平面直角坐标系中,P是反比例函数图象上的一点,把点P绕着顶点O顺时针旋转的对应点落在一次函数图象上,则代数式的值是( )
A. B. C. D.
8.(2022八下·江北期中)如图,△ABC的三个顶点分别为A(1,2)、B(4,2)、C(4,4).若反比例函数y= 在第一象限内的图象与△ABC有交点,则k的取值范围是( )
A.1≤k≤4 B.2≤k≤8 C.2≤k≤16 D.8≤k≤16
9.一定电压(单位:V)下电流和电阻之间成反比例关系,东东用一个蓄电池作为电源组装了一个电路如图1所示,通过实验,发现电流随着电阻值的变化而变化的一组数据如表格所示.
R(Ω) … 2 3 4 6 12 …
I(A) … 24 16 12 a 4 …
下列说法不正确的是( )
A.表中
B.这个蓄电池的电压值是48V
C.图2中图象可以表示电流I和电阻R之间的函数关系
D.若该电路的最小电阻值为1.5Ω,该电路能通过的最大电流是34A
10.(2021·南宁模拟)如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,则k的值是( )
A. B. C. D.
二、填空题
11.(2025九上·樊城期末)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高是物距(小孔到蜡烛的距离)的反比例函数,当时,.若要火焰的像高不低于,则小孔到蜡烛的最大距离为 .
12.(2024七上·吉林期中)一个游泳池的容积为,游泳池注满水所用时间与注水速度 (填“成正比例”、“成反比例”、“不成比例”).
13.(2020九上·路南期末)举出一个生活中应用反比例函数的例子: .
14.(2025·湖北模拟)已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过,那么用电器可变电阻应控制的范围是 .
15.某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为 .
16.(2025九下·浙江月考)如图,过坐标原点的直线AB与反比例函数的图象交于A,B两点(点在第一象限),点为第一象限内,位于直线AB上方反比例函数图象上一点,连结并延长CA交轴于点,连结BC分别交轴、轴于E、F两点,连结AF,若AC的面积为6,则 .
三、计算题
17.(2023八下·亭湖期末)新冠疫情下的中国在全世界抗疫战斗中全方位领跑.某制药公司生产3支单针疫苗和2支双针疫苗需要19min;生产2支单针疫苗和1支双针疫苗需要11min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间?
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/ml)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度首先y与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/ml时,并且不低于23min/ml,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗?请通过计算说明.
四、解答题
18.(2023九下·宜昌模拟)古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力阻力臂动力动力臂(如图).小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为和.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为2米时,撬动石头至少需要多大的力?
(2)若想使动力F不超过(1)中所用力的一半,则动力臂l至少要加长多少?
19.(2025九下·长岭期中)小明欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为和.求动力与动力臂之间的函数解析式.(注:动力动力臂阻力阻力臂)
20.(2025八下·长春月考)人的视觉机能受运动速度的影响很大.行驶中司机在驾驶室内观察前方物体时是动态的,车速增加,视野变窄,当车速为时,视野为80度,如果视野(单位:度)是车速(单位:)的反比例函数.
(1)求与之间的函数关系式:
(2)计算当车速为时视野的度数:
(3)若在某弯道行车时,由于环境的影响,视野的度数至少是100度,求车速最多是多少?
21.(2023八下·睢宁期末)如图,在平面直角坐标系中,、两点在轴的正半轴上,以线段为边向上作正方形,顶点在正比例函数的图像上,反比例函数的图像经过点,且与边相交于点.
(1)若,求点的坐标;
(2)连接,.
①若的面积为24,求的值;
②是否存在某一位置使得,若存在,求出的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】反比例函数的实际应用
2.【答案】A
【知识点】列反比例函数关系式
3.【答案】A
【知识点】反比例函数的实际应用
4.【答案】D
【知识点】反比例函数的实际应用
5.【答案】B
【知识点】反比例函数的实际应用
6.【答案】B
【知识点】反比例函数的图象;反比例函数的实际应用
7.【答案】C
【知识点】列反比例函数关系式;三角形全等及其性质;坐标与图形变化﹣旋转;列一次函数关系式
8.【答案】C
【知识点】待定系数法求反比例函数解析式;反比例函数-动态几何问题
9.【答案】C
【知识点】反比例函数的实际应用
10.【答案】B
【知识点】反比例函数与一次函数的交点问题;反比例函数-动态几何问题
11.【答案】4
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
12.【答案】成反比例
【知识点】反比例函数的实际应用
13.【答案】路程s一定,速度v与时间t之间的关系(答案不唯一)
【知识点】反比例函数的实际应用
14.【答案】
【知识点】反比例函数的实际应用
15.【答案】
【知识点】反比例函数与一次函数的交点问题;反比例函数的实际应用
16.【答案】4
【知识点】待定系数法求一次函数解析式;反比例函数的实际应用;三角形的面积
17.【答案】(1)生产1支单针疫苗需要3min;生产1支双针疫苗需要5min;
(2)小明应在打第二针疫苗的时间段为打第一针后的第13天到第27天内.
【知识点】反比例函数的实际应用;二元一次方程组的实际应用-配套问题
18.【答案】(1)动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)动力臂至少要加长.
【知识点】反比例函数的实际应用
19.【答案】
【知识点】反比例函数的实际应用
20.【答案】(1)
(2)40度
(3)
【知识点】反比例函数的实际应用
21.【答案】(1)解:∵在正方形中,,
∴A点的纵坐标为4,
∵A在直线上,
∴,
∴,
∴,
∴OB=2,
∵在的图像上,
∴,
∴,
∴反比例函数解析式为,
∵,
∴,
∴将代入中,得:,
∴点的坐标为
(2)解:①设,
∴,,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴
解得,
∴;
②不存在,
理由:∵四边形ABCD是正方形,
∴AB=AD,
∵,
∴,
∵,
∴
∴,
∴,
由①可知,,则点
∴,
∴得
∴,
∵,
∴不符合题意,不存在.
【知识点】反比例函数与一次函数的交点问题;三角形全等的判定-ASA;反比例函数-动态几何问题
1.3 反比例函数的应用
一、单选题
1.(2023九下·蔚县模拟)如图1,某长方体A,B,C三个面的面积之比是,当A,B,C三个面分别接触地面时,水平地面所受压强分别为,,.已知满足的函数图象,如图2所示,其中p是压强,F是压力(物体放在水平地面上,物体对地面的压力等于该物体的重力),S是受力面积,则,,的大小关系为( )
A. B. C. D.
2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
A. B. C. D.
3.(2024九上·七里河期末)我们知道压强p,是指物体单位面积S上受到的压力F,即.如果的压力F作用于物体上,产生的压强p要大于,则下列关于物体受力面积的说法正确的是( )
A.S小于 B.S大于 C.S小于 D.S大于
4.(2023九下·裕华模拟)已知闭合电路的电压为定值,电流()与电路的电阻()是反比例函数关系,根据下表判断以下选项正确的是( )
()
()
A.与的关系式为 B.
C. D.当时,
5.(2024九下·石家庄模拟)已知通过电阻R的电流I和电阻两端电压满足关系式,如图所示的四个点分别描述甲、乙、丙、丁四个电阻在不同电路中通过电阻的电流与该电阻阻值的情况,其中描述甲、丙两个电阻的情况点恰好在同一个反比例函数的图象上,则这四个电阻两端的电压最小的是( )
A.甲 B.乙 C.丙 D.丁.
6.小明乘车从广州到北京,行车的平均速度y(km/h)和行车时间x(h)之间的函数图象( )
A.
B.
C.
D.
7.(2024九上·朝阳月考)在平面直角坐标系中,P是反比例函数图象上的一点,把点P绕着顶点O顺时针旋转的对应点落在一次函数图象上,则代数式的值是( )
A. B. C. D.
8.(2022八下·江北期中)如图,△ABC的三个顶点分别为A(1,2)、B(4,2)、C(4,4).若反比例函数y= 在第一象限内的图象与△ABC有交点,则k的取值范围是( )
A.1≤k≤4 B.2≤k≤8 C.2≤k≤16 D.8≤k≤16
9.一定电压(单位:V)下电流和电阻之间成反比例关系,东东用一个蓄电池作为电源组装了一个电路如图1所示,通过实验,发现电流随着电阻值的变化而变化的一组数据如表格所示.
R(Ω) … 2 3 4 6 12 …
I(A) … 24 16 12 a 4 …
下列说法不正确的是( )
A.表中
B.这个蓄电池的电压值是48V
C.图2中图象可以表示电流I和电阻R之间的函数关系
D.若该电路的最小电阻值为1.5Ω,该电路能通过的最大电流是34A
10.(2021·南宁模拟)如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,则k的值是( )
A. B. C. D.
二、填空题
11.(2025九上·樊城期末)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高是物距(小孔到蜡烛的距离)的反比例函数,当时,.若要火焰的像高不低于,则小孔到蜡烛的最大距离为 .
12.(2024七上·吉林期中)一个游泳池的容积为,游泳池注满水所用时间与注水速度 (填“成正比例”、“成反比例”、“不成比例”).
13.(2020九上·路南期末)举出一个生活中应用反比例函数的例子: .
14.(2025·湖北模拟)已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过,那么用电器可变电阻应控制的范围是 .
15.某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为 .
16.(2025九下·浙江月考)如图,过坐标原点的直线AB与反比例函数的图象交于A,B两点(点在第一象限),点为第一象限内,位于直线AB上方反比例函数图象上一点,连结并延长CA交轴于点,连结BC分别交轴、轴于E、F两点,连结AF,若AC的面积为6,则 .
三、计算题
17.(2023八下·亭湖期末)新冠疫情下的中国在全世界抗疫战斗中全方位领跑.某制药公司生产3支单针疫苗和2支双针疫苗需要19min;生产2支单针疫苗和1支双针疫苗需要11min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间?
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/ml)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度首先y与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/ml时,并且不低于23min/ml,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗?请通过计算说明.
四、解答题
18.(2023九下·宜昌模拟)古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力阻力臂动力动力臂(如图).小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为和.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为2米时,撬动石头至少需要多大的力?
(2)若想使动力F不超过(1)中所用力的一半,则动力臂l至少要加长多少?
19.(2025九下·长岭期中)小明欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为和.求动力与动力臂之间的函数解析式.(注:动力动力臂阻力阻力臂)
20.(2025八下·长春月考)人的视觉机能受运动速度的影响很大.行驶中司机在驾驶室内观察前方物体时是动态的,车速增加,视野变窄,当车速为时,视野为80度,如果视野(单位:度)是车速(单位:)的反比例函数.
(1)求与之间的函数关系式:
(2)计算当车速为时视野的度数:
(3)若在某弯道行车时,由于环境的影响,视野的度数至少是100度,求车速最多是多少?
21.(2023八下·睢宁期末)如图,在平面直角坐标系中,、两点在轴的正半轴上,以线段为边向上作正方形,顶点在正比例函数的图像上,反比例函数的图像经过点,且与边相交于点.
(1)若,求点的坐标;
(2)连接,.
①若的面积为24,求的值;
②是否存在某一位置使得,若存在,求出的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】反比例函数的实际应用
2.【答案】A
【知识点】列反比例函数关系式
3.【答案】A
【知识点】反比例函数的实际应用
4.【答案】D
【知识点】反比例函数的实际应用
5.【答案】B
【知识点】反比例函数的实际应用
6.【答案】B
【知识点】反比例函数的图象;反比例函数的实际应用
7.【答案】C
【知识点】列反比例函数关系式;三角形全等及其性质;坐标与图形变化﹣旋转;列一次函数关系式
8.【答案】C
【知识点】待定系数法求反比例函数解析式;反比例函数-动态几何问题
9.【答案】C
【知识点】反比例函数的实际应用
10.【答案】B
【知识点】反比例函数与一次函数的交点问题;反比例函数-动态几何问题
11.【答案】4
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
12.【答案】成反比例
【知识点】反比例函数的实际应用
13.【答案】路程s一定,速度v与时间t之间的关系(答案不唯一)
【知识点】反比例函数的实际应用
14.【答案】
【知识点】反比例函数的实际应用
15.【答案】
【知识点】反比例函数与一次函数的交点问题;反比例函数的实际应用
16.【答案】4
【知识点】待定系数法求一次函数解析式;反比例函数的实际应用;三角形的面积
17.【答案】(1)生产1支单针疫苗需要3min;生产1支双针疫苗需要5min;
(2)小明应在打第二针疫苗的时间段为打第一针后的第13天到第27天内.
【知识点】反比例函数的实际应用;二元一次方程组的实际应用-配套问题
18.【答案】(1)动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)动力臂至少要加长.
【知识点】反比例函数的实际应用
19.【答案】
【知识点】反比例函数的实际应用
20.【答案】(1)
(2)40度
(3)
【知识点】反比例函数的实际应用
21.【答案】(1)解:∵在正方形中,,
∴A点的纵坐标为4,
∵A在直线上,
∴,
∴,
∴,
∴OB=2,
∵在的图像上,
∴,
∴,
∴反比例函数解析式为,
∵,
∴,
∴将代入中,得:,
∴点的坐标为
(2)解:①设,
∴,,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴
解得,
∴;
②不存在,
理由:∵四边形ABCD是正方形,
∴AB=AD,
∵,
∴,
∵,
∴
∴,
∴,
由①可知,,则点
∴,
∴得
∴,
∵,
∴不符合题意,不存在.
【知识点】反比例函数与一次函数的交点问题;三角形全等的判定-ASA;反比例函数-动态几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
1.3 反比例函数的应用
一、单选题
1.(2023九下·蔚县模拟)如图1,某长方体A,B,C三个面的面积之比是,当A,B,C三个面分别接触地面时,水平地面所受压强分别为,,.已知满足的函数图象,如图2所示,其中p是压强,F是压力(物体放在水平地面上,物体对地面的压力等于该物体的重力),S是受力面积,则,,的大小关系为( )
A. B. C. D.
2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
A. B. C. D.
3.(2024九上·七里河期末)我们知道压强p,是指物体单位面积S上受到的压力F,即.如果的压力F作用于物体上,产生的压强p要大于,则下列关于物体受力面积的说法正确的是( )
A.S小于 B.S大于 C.S小于 D.S大于
4.(2023九下·裕华模拟)已知闭合电路的电压为定值,电流()与电路的电阻()是反比例函数关系,根据下表判断以下选项正确的是( )
()
()
A.与的关系式为 B.
C. D.当时,
5.(2024九下·石家庄模拟)已知通过电阻R的电流I和电阻两端电压满足关系式,如图所示的四个点分别描述甲、乙、丙、丁四个电阻在不同电路中通过电阻的电流与该电阻阻值的情况,其中描述甲、丙两个电阻的情况点恰好在同一个反比例函数的图象上,则这四个电阻两端的电压最小的是( )
A.甲 B.乙 C.丙 D.丁.
6.小明乘车从广州到北京,行车的平均速度y(km/h)和行车时间x(h)之间的函数图象( )
A.
B.
C.
D.
7.(2024九上·朝阳月考)在平面直角坐标系中,P是反比例函数图象上的一点,把点P绕着顶点O顺时针旋转的对应点落在一次函数图象上,则代数式的值是( )
A. B. C. D.
8.(2022八下·江北期中)如图,△ABC的三个顶点分别为A(1,2)、B(4,2)、C(4,4).若反比例函数y= 在第一象限内的图象与△ABC有交点,则k的取值范围是( )
A.1≤k≤4 B.2≤k≤8 C.2≤k≤16 D.8≤k≤16
9.一定电压(单位:V)下电流和电阻之间成反比例关系,东东用一个蓄电池作为电源组装了一个电路如图1所示,通过实验,发现电流随着电阻值的变化而变化的一组数据如表格所示.
R(Ω) … 2 3 4 6 12 …
I(A) … 24 16 12 a 4 …
下列说法不正确的是( )
A.表中
B.这个蓄电池的电压值是48V
C.图2中图象可以表示电流I和电阻R之间的函数关系
D.若该电路的最小电阻值为1.5Ω,该电路能通过的最大电流是34A
10.(2021·南宁模拟)如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,则k的值是( )
A. B. C. D.
二、填空题
11.(2025九上·樊城期末)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高是物距(小孔到蜡烛的距离)的反比例函数,当时,.若要火焰的像高不低于,则小孔到蜡烛的最大距离为 .
12.(2024七上·吉林期中)一个游泳池的容积为,游泳池注满水所用时间与注水速度 (填“成正比例”、“成反比例”、“不成比例”).
13.(2020九上·路南期末)举出一个生活中应用反比例函数的例子: .
14.(2025·湖北模拟)已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过,那么用电器可变电阻应控制的范围是 .
15.某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为 .
16.(2025九下·浙江月考)如图,过坐标原点的直线AB与反比例函数的图象交于A,B两点(点在第一象限),点为第一象限内,位于直线AB上方反比例函数图象上一点,连结并延长CA交轴于点,连结BC分别交轴、轴于E、F两点,连结AF,若AC的面积为6,则 .
三、计算题
17.(2023八下·亭湖期末)新冠疫情下的中国在全世界抗疫战斗中全方位领跑.某制药公司生产3支单针疫苗和2支双针疫苗需要19min;生产2支单针疫苗和1支双针疫苗需要11min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间?
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/ml)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度首先y与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/ml时,并且不低于23min/ml,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗?请通过计算说明.
四、解答题
18.(2023九下·宜昌模拟)古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力阻力臂动力动力臂(如图).小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为和.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为2米时,撬动石头至少需要多大的力?
(2)若想使动力F不超过(1)中所用力的一半,则动力臂l至少要加长多少?
19.(2025九下·长岭期中)小明欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为和.求动力与动力臂之间的函数解析式.(注:动力动力臂阻力阻力臂)
20.(2025八下·长春月考)人的视觉机能受运动速度的影响很大.行驶中司机在驾驶室内观察前方物体时是动态的,车速增加,视野变窄,当车速为时,视野为80度,如果视野(单位:度)是车速(单位:)的反比例函数.
(1)求与之间的函数关系式:
(2)计算当车速为时视野的度数:
(3)若在某弯道行车时,由于环境的影响,视野的度数至少是100度,求车速最多是多少?
21.(2023八下·睢宁期末)如图,在平面直角坐标系中,、两点在轴的正半轴上,以线段为边向上作正方形,顶点在正比例函数的图像上,反比例函数的图像经过点,且与边相交于点.
(1)若,求点的坐标;
(2)连接,.
①若的面积为24,求的值;
②是否存在某一位置使得,若存在,求出的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】反比例函数的实际应用
2.【答案】A
【知识点】列反比例函数关系式
3.【答案】A
【知识点】反比例函数的实际应用
4.【答案】D
【知识点】反比例函数的实际应用
5.【答案】B
【知识点】反比例函数的实际应用
6.【答案】B
【知识点】反比例函数的图象;反比例函数的实际应用
7.【答案】C
【知识点】列反比例函数关系式;三角形全等及其性质;坐标与图形变化﹣旋转;列一次函数关系式
8.【答案】C
【知识点】待定系数法求反比例函数解析式;反比例函数-动态几何问题
9.【答案】C
【知识点】反比例函数的实际应用
10.【答案】B
【知识点】反比例函数与一次函数的交点问题;反比例函数-动态几何问题
11.【答案】4
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
12.【答案】成反比例
【知识点】反比例函数的实际应用
13.【答案】路程s一定,速度v与时间t之间的关系(答案不唯一)
【知识点】反比例函数的实际应用
14.【答案】
【知识点】反比例函数的实际应用
15.【答案】
【知识点】反比例函数与一次函数的交点问题;反比例函数的实际应用
16.【答案】4
【知识点】待定系数法求一次函数解析式;反比例函数的实际应用;三角形的面积
17.【答案】(1)生产1支单针疫苗需要3min;生产1支双针疫苗需要5min;
(2)小明应在打第二针疫苗的时间段为打第一针后的第13天到第27天内.
【知识点】反比例函数的实际应用;二元一次方程组的实际应用-配套问题
18.【答案】(1)动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)动力臂至少要加长.
【知识点】反比例函数的实际应用
19.【答案】
【知识点】反比例函数的实际应用
20.【答案】(1)
(2)40度
(3)
【知识点】反比例函数的实际应用
21.【答案】(1)解:∵在正方形中,,
∴A点的纵坐标为4,
∵A在直线上,
∴,
∴,
∴,
∴OB=2,
∵在的图像上,
∴,
∴,
∴反比例函数解析式为,
∵,
∴,
∴将代入中,得:,
∴点的坐标为
(2)解:①设,
∴,,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴
解得,
∴;
②不存在,
理由:∵四边形ABCD是正方形,
∴AB=AD,
∵,
∴,
∵,
∴
∴,
∴,
由①可知,,则点
∴,
∴得
∴,
∵,
∴不符合题意,不存在.
【知识点】反比例函数与一次函数的交点问题;三角形全等的判定-ASA;反比例函数-动态几何问题
1.3 反比例函数的应用
一、单选题
1.(2023九下·蔚县模拟)如图1,某长方体A,B,C三个面的面积之比是,当A,B,C三个面分别接触地面时,水平地面所受压强分别为,,.已知满足的函数图象,如图2所示,其中p是压强,F是压力(物体放在水平地面上,物体对地面的压力等于该物体的重力),S是受力面积,则,,的大小关系为( )
A. B. C. D.
2.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
A. B. C. D.
3.(2024九上·七里河期末)我们知道压强p,是指物体单位面积S上受到的压力F,即.如果的压力F作用于物体上,产生的压强p要大于,则下列关于物体受力面积的说法正确的是( )
A.S小于 B.S大于 C.S小于 D.S大于
4.(2023九下·裕华模拟)已知闭合电路的电压为定值,电流()与电路的电阻()是反比例函数关系,根据下表判断以下选项正确的是( )
()
()
A.与的关系式为 B.
C. D.当时,
5.(2024九下·石家庄模拟)已知通过电阻R的电流I和电阻两端电压满足关系式,如图所示的四个点分别描述甲、乙、丙、丁四个电阻在不同电路中通过电阻的电流与该电阻阻值的情况,其中描述甲、丙两个电阻的情况点恰好在同一个反比例函数的图象上,则这四个电阻两端的电压最小的是( )
A.甲 B.乙 C.丙 D.丁.
6.小明乘车从广州到北京,行车的平均速度y(km/h)和行车时间x(h)之间的函数图象( )
A.
B.
C.
D.
7.(2024九上·朝阳月考)在平面直角坐标系中,P是反比例函数图象上的一点,把点P绕着顶点O顺时针旋转的对应点落在一次函数图象上,则代数式的值是( )
A. B. C. D.
8.(2022八下·江北期中)如图,△ABC的三个顶点分别为A(1,2)、B(4,2)、C(4,4).若反比例函数y= 在第一象限内的图象与△ABC有交点,则k的取值范围是( )
A.1≤k≤4 B.2≤k≤8 C.2≤k≤16 D.8≤k≤16
9.一定电压(单位:V)下电流和电阻之间成反比例关系,东东用一个蓄电池作为电源组装了一个电路如图1所示,通过实验,发现电流随着电阻值的变化而变化的一组数据如表格所示.
R(Ω) … 2 3 4 6 12 …
I(A) … 24 16 12 a 4 …
下列说法不正确的是( )
A.表中
B.这个蓄电池的电压值是48V
C.图2中图象可以表示电流I和电阻R之间的函数关系
D.若该电路的最小电阻值为1.5Ω,该电路能通过的最大电流是34A
10.(2021·南宁模拟)如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,则k的值是( )
A. B. C. D.
二、填空题
11.(2025九上·樊城期末)如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高是物距(小孔到蜡烛的距离)的反比例函数,当时,.若要火焰的像高不低于,则小孔到蜡烛的最大距离为 .
12.(2024七上·吉林期中)一个游泳池的容积为,游泳池注满水所用时间与注水速度 (填“成正比例”、“成反比例”、“不成比例”).
13.(2020九上·路南期末)举出一个生活中应用反比例函数的例子: .
14.(2025·湖北模拟)已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过,那么用电器可变电阻应控制的范围是 .
15.某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为 .
16.(2025九下·浙江月考)如图,过坐标原点的直线AB与反比例函数的图象交于A,B两点(点在第一象限),点为第一象限内,位于直线AB上方反比例函数图象上一点,连结并延长CA交轴于点,连结BC分别交轴、轴于E、F两点,连结AF,若AC的面积为6,则 .
三、计算题
17.(2023八下·亭湖期末)新冠疫情下的中国在全世界抗疫战斗中全方位领跑.某制药公司生产3支单针疫苗和2支双针疫苗需要19min;生产2支单针疫苗和1支双针疫苗需要11min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间?
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:min/ml)与时间x(单位:天)的函数关系如图所示:疫苗注射后体内抗体浓度首先y与x成一次函数关系,体内抗体到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50min/ml时,并且不低于23min/ml,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.请问:小明可以在哪个时间段内打第二针疫苗?请通过计算说明.
四、解答题
18.(2023九下·宜昌模拟)古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力阻力臂动力动力臂(如图).小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为和.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为2米时,撬动石头至少需要多大的力?
(2)若想使动力F不超过(1)中所用力的一半,则动力臂l至少要加长多少?
19.(2025九下·长岭期中)小明欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为和.求动力与动力臂之间的函数解析式.(注:动力动力臂阻力阻力臂)
20.(2025八下·长春月考)人的视觉机能受运动速度的影响很大.行驶中司机在驾驶室内观察前方物体时是动态的,车速增加,视野变窄,当车速为时,视野为80度,如果视野(单位:度)是车速(单位:)的反比例函数.
(1)求与之间的函数关系式:
(2)计算当车速为时视野的度数:
(3)若在某弯道行车时,由于环境的影响,视野的度数至少是100度,求车速最多是多少?
21.(2023八下·睢宁期末)如图,在平面直角坐标系中,、两点在轴的正半轴上,以线段为边向上作正方形,顶点在正比例函数的图像上,反比例函数的图像经过点,且与边相交于点.
(1)若,求点的坐标;
(2)连接,.
①若的面积为24,求的值;
②是否存在某一位置使得,若存在,求出的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】反比例函数的实际应用
2.【答案】A
【知识点】列反比例函数关系式
3.【答案】A
【知识点】反比例函数的实际应用
4.【答案】D
【知识点】反比例函数的实际应用
5.【答案】B
【知识点】反比例函数的实际应用
6.【答案】B
【知识点】反比例函数的图象;反比例函数的实际应用
7.【答案】C
【知识点】列反比例函数关系式;三角形全等及其性质;坐标与图形变化﹣旋转;列一次函数关系式
8.【答案】C
【知识点】待定系数法求反比例函数解析式;反比例函数-动态几何问题
9.【答案】C
【知识点】反比例函数的实际应用
10.【答案】B
【知识点】反比例函数与一次函数的交点问题;反比例函数-动态几何问题
11.【答案】4
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
12.【答案】成反比例
【知识点】反比例函数的实际应用
13.【答案】路程s一定,速度v与时间t之间的关系(答案不唯一)
【知识点】反比例函数的实际应用
14.【答案】
【知识点】反比例函数的实际应用
15.【答案】
【知识点】反比例函数与一次函数的交点问题;反比例函数的实际应用
16.【答案】4
【知识点】待定系数法求一次函数解析式;反比例函数的实际应用;三角形的面积
17.【答案】(1)生产1支单针疫苗需要3min;生产1支双针疫苗需要5min;
(2)小明应在打第二针疫苗的时间段为打第一针后的第13天到第27天内.
【知识点】反比例函数的实际应用;二元一次方程组的实际应用-配套问题
18.【答案】(1)动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)动力臂至少要加长.
【知识点】反比例函数的实际应用
19.【答案】
【知识点】反比例函数的实际应用
20.【答案】(1)
(2)40度
(3)
【知识点】反比例函数的实际应用
21.【答案】(1)解:∵在正方形中,,
∴A点的纵坐标为4,
∵A在直线上,
∴,
∴,
∴,
∴OB=2,
∵在的图像上,
∴,
∴,
∴反比例函数解析式为,
∵,
∴,
∴将代入中,得:,
∴点的坐标为
(2)解:①设,
∴,,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴
解得,
∴;
②不存在,
理由:∵四边形ABCD是正方形,
∴AB=AD,
∵,
∴,
∵,
∴
∴,
∴,
由①可知,,则点
∴,
∴得
∴,
∵,
∴不符合题意,不存在.
【知识点】反比例函数与一次函数的交点问题;三角形全等的判定-ASA;反比例函数-动态几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
