第1章 反比例函数测试题（含答案）

中小学教育资源及组卷应用平台
第1章 反比例函数测试题
一、单选题
1．（2024九上·东平月考）如图，A，B两点在反比例函数的图象上，C、D两点在反比例函数的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF=，则=（　　）
A．4 B． C． D．6
2．（2022·东丽模拟）若点，，都在反比例函数的图象上，则，，的大小关系是（　　）
A． B． C． D．
3．（2023九上·岑溪月考）如果反比例函数y＝（a是常数）的图象在第二、四象限，那么a的取值范围是（　　）
A．a＞2 B．a＜2 C．a＞0 D．a＜0
4．（2025九下·潮南月考）如图，反比例函数的图象经过点，当时，的取值范围是(　　)
A．或 B． C． D．
5．（2021·香坊模拟）如果反比例函数y= 的图象经过点(-1，-2)，则k的值是（　　）
A．2 B．-2 C．-3 D．3
6．关于函数，下列说法不正确的是（　　）
A．当时，y随x的增大而增大
B．当时，y随x的增大而增大
C．当时，若x越大，则对应的y值也越大
D．若、是其图象上两点，则不一定有
7．（2021九上·定州期末）已知点A（x1，y1），B（x2，y2）是双曲线 上的两点，若x2＜0＜x1，则有（　　）
A．0＜y1＜y2 B．0＜y2＜y1 C．y2＜0＜y1 D．y1＜0＜y2
8．（2023九上·牧野期末）如图，点是函数（）图像上一点，点是函数（，）图像上一点，点在轴上，连接，，．若轴，，则（　　）
A．4 B．2 C．2.5 D．5
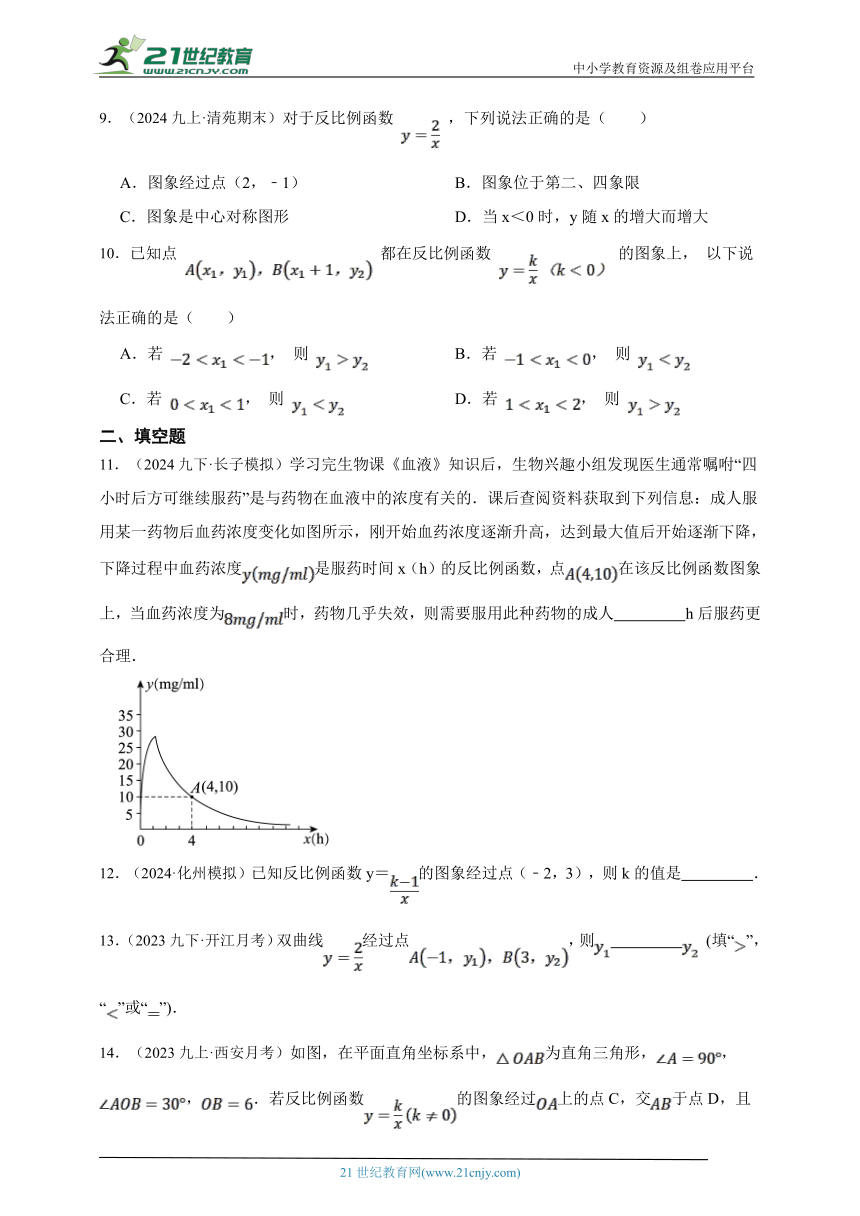
9．（2024九上·清苑期末）对于反比例函数 ，下列说法正确的是（　　）
A．图象经过点（2，﹣1） B．图象位于第二、四象限
C．图象是中心对称图形 D．当x＜0时，y随x的增大而增大
10．已知点 都在反比例函数 的图象上， 以下说法正确的是（　　）
A．若 ， 则 B．若 ， 则
C．若 ， 则 D．若 ， 则
二、填空题
11．（2024九下·长子模拟）学习完生物课《血液》知识后，生物兴趣小组发现医生通常嘱咐“四小时后方可继续服药”是与药物在血液中的浓度有关的．课后查阅资料获取到下列信息：成人服用某一药物后血药浓度变化如图所示，刚开始血药浓度逐渐升高，达到最大值后开始逐渐下降，下降过程中血药浓度是服药时间x（h）的反比例函数，点在该反比例函数图象上，当血药浓度为时，药物几乎失效，则需要服用此种药物的成人　 　h后服药更合理．
12．（2024·化州模拟）已知反比例函数y＝的图象经过点（﹣2，3），则k的值是　 　．
13．（2023九下·开江月考）双曲线经过点，则　 　 (填“”，“”或“”)．
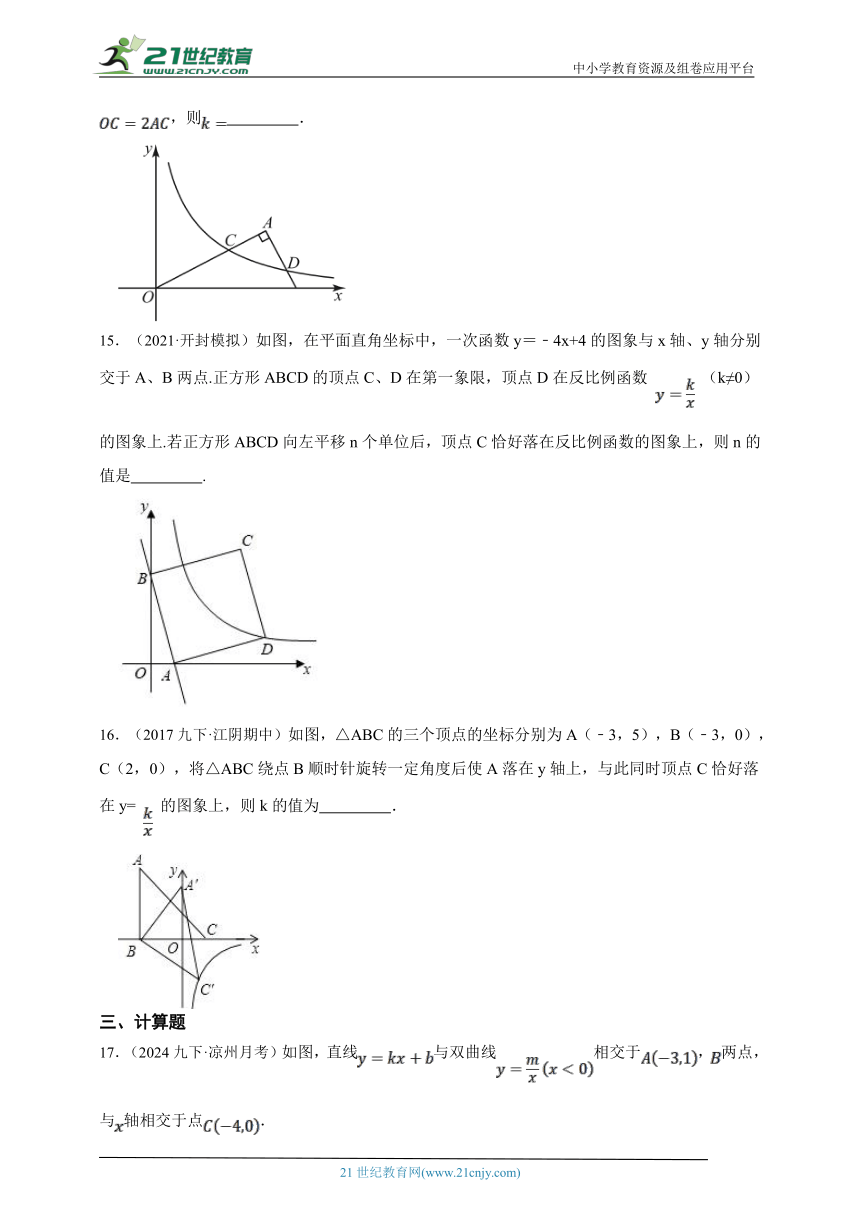
14．（2023九上·西安月考）如图，在平面直角坐标系中，为直角三角形，，，．若反比例函数的图象经过上的点C，交于点D，且，则　 　．
15．（2021·开封模拟）如图，在平面直角坐标中，一次函数y＝﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限，顶点D在反比例函数 （k≠0）的图象上.若正方形ABCD向左平移n个单位后，顶点C恰好落在反比例函数的图象上，则n的值是　 　.
16．（2017九下·江阴期中）如图，△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣3，0），C（2，0），将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在y= 的图象上，则k的值为　 　．
三、计算题
17．（2024九下·凉州月考）如图，直线与双曲线相交于，两点，与轴相交于点．
（1）求反比例函数的解析式；
（2）求一次函数的解析式；
（3）连接，求的面积．
18．（2022九下·广州模拟）已知
（1）化简A．
（2）若点在直线与反比例的图象的交点，求A值．
19．（2024九上·丹东期末）如图，一次函数的图象与反比例函数的图象在第二象限内交于点，，为轴正半轴上一点，连接，，的面积为6．
（1）求的值及一次函数的表达式；
（2）求点的坐标；
（3）若为反比例函数图象上的一点，为轴上一点，是否存在点，，使以，，，为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由．
四、解答题
20．（2025·渭源模拟）如图，在平面直角坐标系中，已知正比例函数的图象与反比例函数的图象交于两点．
（1）求反比例函数的解析式和点的坐标；
（2）结合图象，请直接写出不等式的解集．
21．（2023九上·祁阳期中）如图，已知一次函数y1＝kx＋b与反比例函数y2＝的图象交于、两点．分别求出y1和y2的解析式．
22．（2021·玉林）先化简再求值： ，其中a使反比例函数 的图象分别位于第二、四象限.
23．（2024·成都模拟）已知直线与x轴相交于点A，与双曲线相交于点B．
（1）若，请直接写出当时，x的取值范围；
（2）如图，以为边在直线l上方作正方形，点D恰好落在反比例函数的图象上，求k的值；
（3）在（2）的条件下，将正方形沿着射线的方向平移，当点C落在反比例函数的图象上时，试求出此时的平移距离．
答案解析部分
1．【答案】A
【知识点】反比例函数的性质；反比例函数系数k的几何意义
2．【答案】D
【知识点】反比例函数的性质
3．【答案】B
【知识点】反比例函数的性质
4．【答案】A
【知识点】反比例函数的图象
5．【答案】D
【知识点】待定系数法求反比例函数解析式
6．【答案】C
【知识点】反比例函数的图象；反比例函数的性质；反比例函数图象上点的坐标特征
7．【答案】D
【知识点】反比例函数的性质
8．【答案】D
【知识点】反比例函数系数k的几何意义
9．【答案】C
【知识点】反比例函数的图象；反比例函数图象的对称性；反比例函数的性质；反比例函数图象上点的坐标特征
10．【答案】C
【知识点】反比例函数的性质；反比例函数图象上点的坐标特征
11．【答案】5
【知识点】反比例函数的实际应用
12．【答案】-5
【知识点】待定系数法求反比例函数解析式
13．【答案】
【知识点】反比例函数的性质
14．【答案】
【知识点】待定系数法求反比例函数解析式；含30°角的直角三角形；勾股定理
15．【答案】3
【知识点】反比例函数的性质；全等三角形的判定与性质；正方形的性质
16．【答案】-3
【知识点】反比例函数图象上点的坐标特征
17．【答案】（1）
（2）
（3）的面积为4
【知识点】待定系数法求一次函数解析式；待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
18．【答案】（1）
（2）
【知识点】分式的化简求值；反比例函数与一次函数的交点问题
19．【答案】（1），一次函数的表达式为
（2）
（3）
【知识点】待定系数法求一次函数解析式；反比例函数与一次函数的交点问题；平行四边形的性质
20．【答案】（1），；
（2）或．
【知识点】反比例函数的性质；待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
21．【答案】，．
【知识点】待定系数法求一次函数解析式；待定系数法求反比例函数解析式
22．【答案】解：∵a使反比例函数 的图象分别位于第二、四象限，
∴ ，
∴
=
= .
【知识点】分式的混合运算；反比例函数的性质
23．【答案】（1）或
（2）解：分别过点作轴、轴，如图所示：
当时，则，解得
∴点的坐标为
∵轴、轴，
∴，
∵四边形是正方形
∴
∴
∴
设，则
∴
则
∴
∵在直线上
∴
∴
∵点和点在上
则
∵
∴
∵
∴
解得
把代入
解出
（3）解：∵在（2）的条件下，将正方形沿着射线的方向平移，当点C落在反比例函数的图象上时，∴此时的平移距离
∵，，
∴，
在中，
即此时的平移距离为
【知识点】反比例函数与一次函数的交点问题；正方形的性质
第1章 反比例函数测试题
一、单选题
1．（2024九上·东平月考）如图，A，B两点在反比例函数的图象上，C、D两点在反比例函数的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF=，则=（　　）
A．4 B． C． D．6
2．（2022·东丽模拟）若点，，都在反比例函数的图象上，则，，的大小关系是（　　）
A． B． C． D．
3．（2023九上·岑溪月考）如果反比例函数y＝（a是常数）的图象在第二、四象限，那么a的取值范围是（　　）
A．a＞2 B．a＜2 C．a＞0 D．a＜0
4．（2025九下·潮南月考）如图，反比例函数的图象经过点，当时，的取值范围是(　　)
A．或 B． C． D．
5．（2021·香坊模拟）如果反比例函数y= 的图象经过点(-1，-2)，则k的值是（　　）
A．2 B．-2 C．-3 D．3
6．关于函数，下列说法不正确的是（　　）
A．当时，y随x的增大而增大
B．当时，y随x的增大而增大
C．当时，若x越大，则对应的y值也越大
D．若、是其图象上两点，则不一定有
7．（2021九上·定州期末）已知点A（x1，y1），B（x2，y2）是双曲线 上的两点，若x2＜0＜x1，则有（　　）
A．0＜y1＜y2 B．0＜y2＜y1 C．y2＜0＜y1 D．y1＜0＜y2
8．（2023九上·牧野期末）如图，点是函数（）图像上一点，点是函数（，）图像上一点，点在轴上，连接，，．若轴，，则（　　）
A．4 B．2 C．2.5 D．5
9．（2024九上·清苑期末）对于反比例函数 ，下列说法正确的是（　　）
A．图象经过点（2，﹣1） B．图象位于第二、四象限
C．图象是中心对称图形 D．当x＜0时，y随x的增大而增大
10．已知点 都在反比例函数 的图象上， 以下说法正确的是（　　）
A．若 ， 则 B．若 ， 则
C．若 ， 则 D．若 ， 则
二、填空题
11．（2024九下·长子模拟）学习完生物课《血液》知识后，生物兴趣小组发现医生通常嘱咐“四小时后方可继续服药”是与药物在血液中的浓度有关的．课后查阅资料获取到下列信息：成人服用某一药物后血药浓度变化如图所示，刚开始血药浓度逐渐升高，达到最大值后开始逐渐下降，下降过程中血药浓度是服药时间x（h）的反比例函数，点在该反比例函数图象上，当血药浓度为时，药物几乎失效，则需要服用此种药物的成人　 　h后服药更合理．
12．（2024·化州模拟）已知反比例函数y＝的图象经过点（﹣2，3），则k的值是　 　．
13．（2023九下·开江月考）双曲线经过点，则　 　 (填“”，“”或“”)．
14．（2023九上·西安月考）如图，在平面直角坐标系中，为直角三角形，，，．若反比例函数的图象经过上的点C，交于点D，且，则　 　．
15．（2021·开封模拟）如图，在平面直角坐标中，一次函数y＝﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限，顶点D在反比例函数 （k≠0）的图象上.若正方形ABCD向左平移n个单位后，顶点C恰好落在反比例函数的图象上，则n的值是　 　.
16．（2017九下·江阴期中）如图，△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣3，0），C（2，0），将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在y= 的图象上，则k的值为　 　．
三、计算题
17．（2024九下·凉州月考）如图，直线与双曲线相交于，两点，与轴相交于点．
（1）求反比例函数的解析式；
（2）求一次函数的解析式；
（3）连接，求的面积．
18．（2022九下·广州模拟）已知
（1）化简A．
（2）若点在直线与反比例的图象的交点，求A值．
19．（2024九上·丹东期末）如图，一次函数的图象与反比例函数的图象在第二象限内交于点，，为轴正半轴上一点，连接，，的面积为6．
（1）求的值及一次函数的表达式；
（2）求点的坐标；
（3）若为反比例函数图象上的一点，为轴上一点，是否存在点，，使以，，，为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由．
四、解答题
20．（2025·渭源模拟）如图，在平面直角坐标系中，已知正比例函数的图象与反比例函数的图象交于两点．
（1）求反比例函数的解析式和点的坐标；
（2）结合图象，请直接写出不等式的解集．
21．（2023九上·祁阳期中）如图，已知一次函数y1＝kx＋b与反比例函数y2＝的图象交于、两点．分别求出y1和y2的解析式．
22．（2021·玉林）先化简再求值： ，其中a使反比例函数 的图象分别位于第二、四象限.
23．（2024·成都模拟）已知直线与x轴相交于点A，与双曲线相交于点B．
（1）若，请直接写出当时，x的取值范围；
（2）如图，以为边在直线l上方作正方形，点D恰好落在反比例函数的图象上，求k的值；
（3）在（2）的条件下，将正方形沿着射线的方向平移，当点C落在反比例函数的图象上时，试求出此时的平移距离．
答案解析部分
1．【答案】A
【知识点】反比例函数的性质；反比例函数系数k的几何意义
2．【答案】D
【知识点】反比例函数的性质
3．【答案】B
【知识点】反比例函数的性质
4．【答案】A
【知识点】反比例函数的图象
5．【答案】D
【知识点】待定系数法求反比例函数解析式
6．【答案】C
【知识点】反比例函数的图象；反比例函数的性质；反比例函数图象上点的坐标特征
7．【答案】D
【知识点】反比例函数的性质
8．【答案】D
【知识点】反比例函数系数k的几何意义
9．【答案】C
【知识点】反比例函数的图象；反比例函数图象的对称性；反比例函数的性质；反比例函数图象上点的坐标特征
10．【答案】C
【知识点】反比例函数的性质；反比例函数图象上点的坐标特征
11．【答案】5
【知识点】反比例函数的实际应用
12．【答案】-5
【知识点】待定系数法求反比例函数解析式
13．【答案】
【知识点】反比例函数的性质
14．【答案】
【知识点】待定系数法求反比例函数解析式；含30°角的直角三角形；勾股定理
15．【答案】3
【知识点】反比例函数的性质；全等三角形的判定与性质；正方形的性质
16．【答案】-3
【知识点】反比例函数图象上点的坐标特征
17．【答案】（1）
（2）
（3）的面积为4
【知识点】待定系数法求一次函数解析式；待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
18．【答案】（1）
（2）
【知识点】分式的化简求值；反比例函数与一次函数的交点问题
19．【答案】（1），一次函数的表达式为
（2）
（3）
【知识点】待定系数法求一次函数解析式；反比例函数与一次函数的交点问题；平行四边形的性质
20．【答案】（1），；
（2）或．
【知识点】反比例函数的性质；待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
21．【答案】，．
【知识点】待定系数法求一次函数解析式；待定系数法求反比例函数解析式
22．【答案】解：∵a使反比例函数 的图象分别位于第二、四象限，
∴ ，
∴
=
= .
【知识点】分式的混合运算；反比例函数的性质
23．【答案】（1）或
（2）解：分别过点作轴、轴，如图所示：
当时，则，解得
∴点的坐标为
∵轴、轴，
∴，
∵四边形是正方形
∴
∴
∴
设，则
∴
则
∴
∵在直线上
∴
∴
∵点和点在上
则
∵
∴
∵
∴
解得
把代入
解出
（3）解：∵在（2）的条件下，将正方形沿着射线的方向平移，当点C落在反比例函数的图象上时，∴此时的平移距离
∵，，
∴，
在中，
即此时的平移距离为
【知识点】反比例函数与一次函数的交点问题；正方形的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)