15.2线段的垂直平分线 课件(共17张PPT) 沪科版(2024)数学八年级上册
文档属性
| 名称 | 15.2线段的垂直平分线 课件(共17张PPT) 沪科版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 21.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-15 11:16:34 | ||
图片预览


文档简介
(共17张PPT)
15.2 线段的垂直平分线
5、草稿本
3、三角尺
2、圆规
4、铅笔
准备
请同学们准备好下列学习用品:
1、直尺
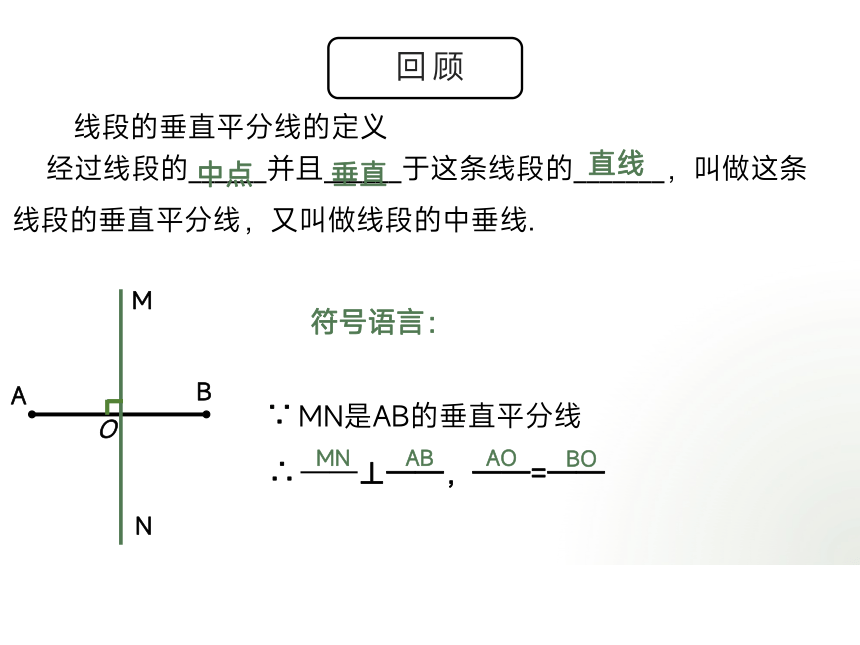
线段的垂直平分线的定义
经过线段的______并且______于这条线段的_______,叫做这条线段的垂直平分线,又叫做线段的中垂线.
A
B
M
O
N
符号语言:
∵ MN是AB的垂直平分线
∴ ——⊥——,——=——
MN
AB
AO
BO
中点
垂直
直线
回顾
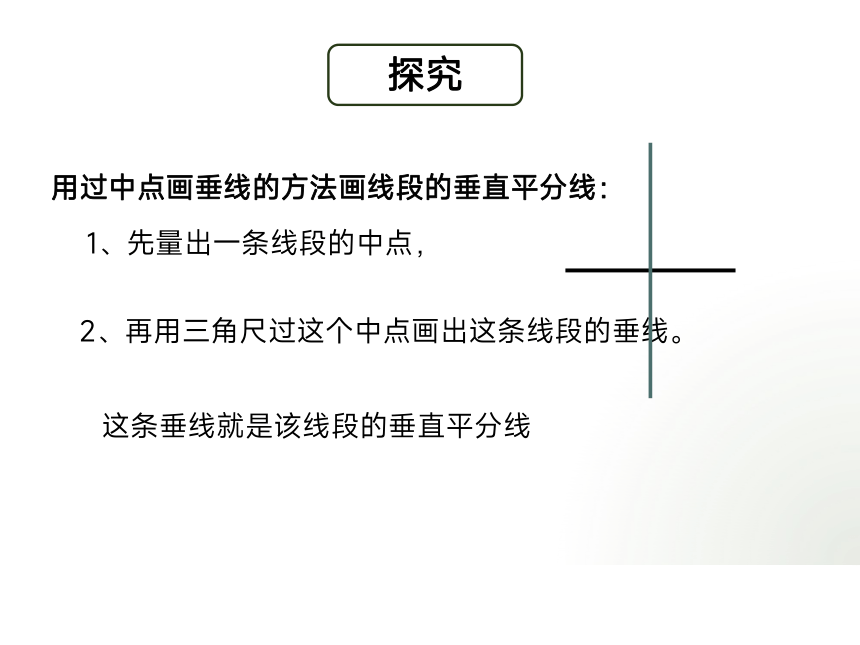
用过中点画垂线的方法画线段的垂直平分线:
2、再用三角尺过这个中点画出这条线段的垂线。
探究
1、先量出一条线段的中点,
这条垂线就是该线段的垂直平分线
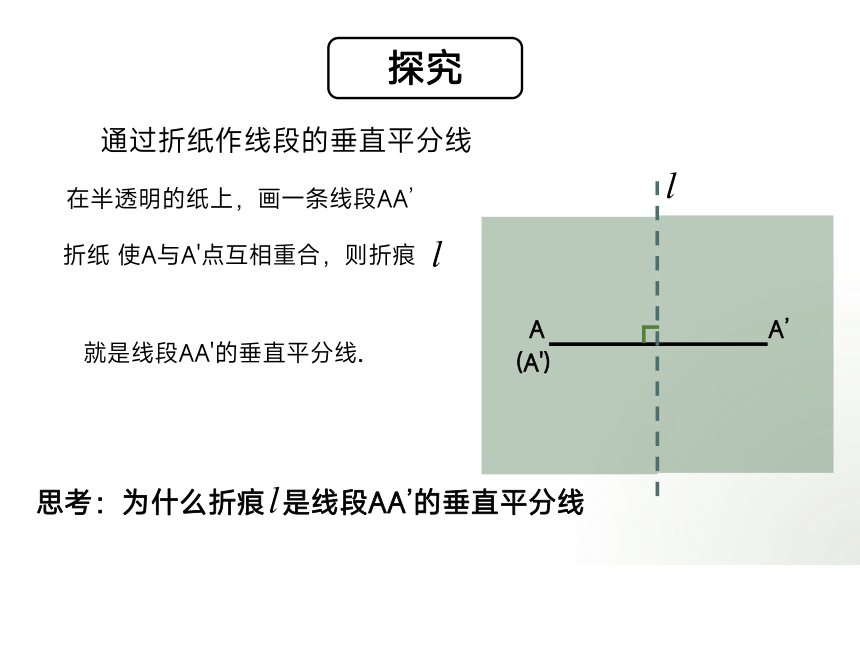
折纸 使A与A'点互相重合,则折痕
A’
通过折纸作线段的垂直平分线
A
(A')
就是线段AA'的垂直平分线.
在半透明的纸上,画一条线段AA’
思考:为什么折痕 是线段AA’的垂直平分线
探究
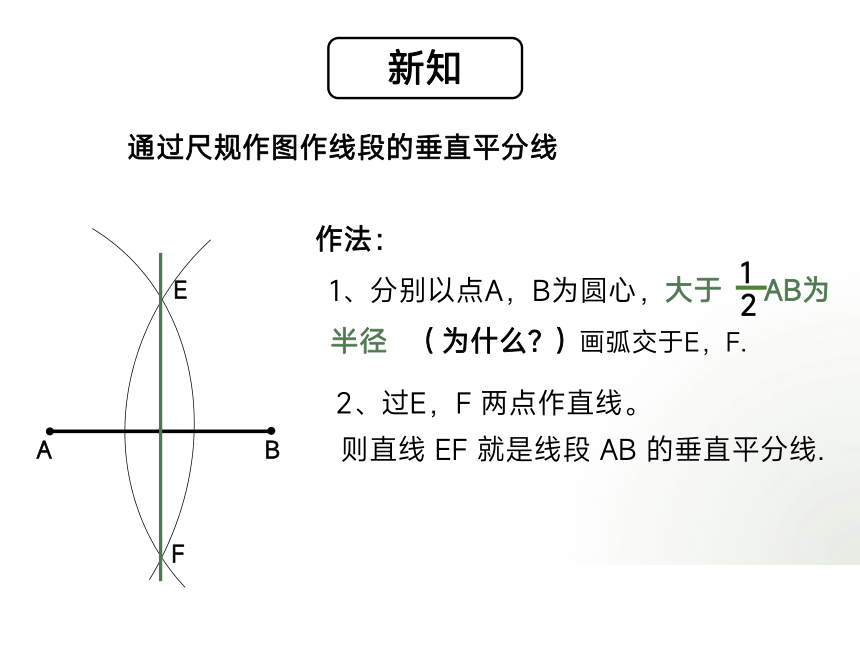
大于 AB为半径
作法:
1、分别以点A,B为圆心,
2、过E,F 两点作直线。
则直线 EF 就是线段 AB 的垂直平分线.
1
2
( 为什么?)
画弧交于E,F.
A
B
E
F
通过尺规作图作线段的垂直平分线
新知
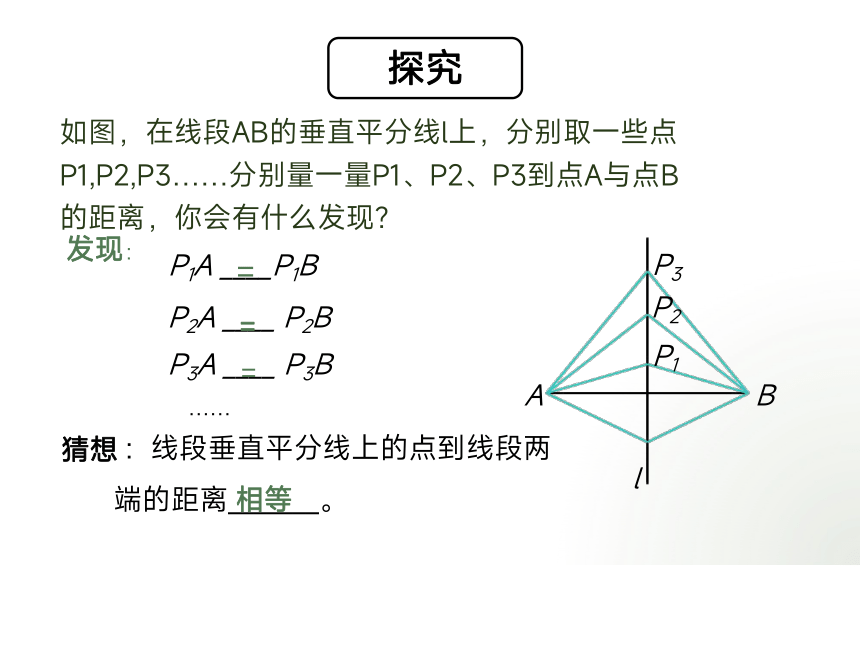
如图,在线段AB的垂直平分线l上,分别取一些点P1,P2,P3……分别量一量P1、P2、P3到点A与点B的距离,你会有什么发现?
:线段垂直平分线上的点到线段两端的距离_______。
发现:
相等
探究
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
……
=
=
=
猜想
猜想:线段垂直平分线上的点到线段两端的距离相等。
A
M
P
B
O
已知:如图,直线 MN 是线段 AB 的垂直平分线, P 是 MN 上任意一点 .
求证:PA =PB.
当P不与O重合时,可以通过证明△AOP ≌ △BOP,得到PA =PB
探究
N
分析:
P
A
B
M
O
N
证明:
∵ MN⊥AB
∴ AO=OB
在 AOP和 BOP 中,
AO=OB
∠AOP= ∠BOP
PO=PO
∴ AOP ≌ BOP
∴ PA=PB
∵
(SAS)
(垂直的定义)
(已证)
(已证)
(公共边)
(全等三角形的对应边相等)
∵ MN是线段 AB 的垂直平分线
∴ ∠AOP= ∠BOP=90
1、当P与O重合时,显然PA=PB
2、当P不与O重合时,
条件:
点在线段的垂直平分线上.
结论:
这个点到线段两端点的距离相等.
N
线段的垂直平分线的性质定理:
线段的垂直平分线上的点到线段两端的距离相等。
符号语言:
∵ MN⊥AB于O,OA=OB
(或者说MN是线段AB的垂直平分线)
∴ ____=_____
M
B
P
A
O
新知
PA
PB
1、完成填空并说明理由。
如图:已知直线l垂直平分线段AB,P是l上一点,若PA=1,
则PB=______
P
A
B
l
C
练习
理由:_______________________________________________________________
2、如图,在 ABC 中,AB边 的垂直平分线 DE 分别交 AB,AC 于点 E,D.
(1)BD+CD与AC的长有什么关系?
例题
2、如图,在 ABC 中,DE是边AB 的垂直平分线 ,分别 交 AB,AC 于点 E,D.
(2)若BC=8,AC=10,则 BCD周长为多少?
例题
收获
当线段的垂直平分线和三角形的周长同时出现时,可以借助垂直平分线的性质,将三角形中某两边的和等量代换成一条边的长,进而借助整体的思想求解相关问题。
变式
1、如图所示,在 △ABC 中,AB,AC 的垂直平分线分别交BC 于 D,E,垂足分别是 M,N.
若 ADE的周长是10,则BC的长为多少?
小结
1、运用尺规作图,作线段的垂直平分线的方法。
A
B
E
F
2、线段的垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等。
P
A
B
l
C
作业
基础巩固;课本P131,习题15.2第2题
拓展提高:课本P131,习题15.2第4题
自主探究:
1、预习课本P129-130内容
2、思考:你能写出线段垂直平分线性质定理的逆命题吗?它是真命题吗?
15.2 线段的垂直平分线
5、草稿本
3、三角尺
2、圆规
4、铅笔
准备
请同学们准备好下列学习用品:
1、直尺
线段的垂直平分线的定义
经过线段的______并且______于这条线段的_______,叫做这条线段的垂直平分线,又叫做线段的中垂线.
A
B
M
O
N
符号语言:
∵ MN是AB的垂直平分线
∴ ——⊥——,——=——
MN
AB
AO
BO
中点
垂直
直线
回顾
用过中点画垂线的方法画线段的垂直平分线:
2、再用三角尺过这个中点画出这条线段的垂线。
探究
1、先量出一条线段的中点,
这条垂线就是该线段的垂直平分线
折纸 使A与A'点互相重合,则折痕
A’
通过折纸作线段的垂直平分线
A
(A')
就是线段AA'的垂直平分线.
在半透明的纸上,画一条线段AA’
思考:为什么折痕 是线段AA’的垂直平分线
探究
大于 AB为半径
作法:
1、分别以点A,B为圆心,
2、过E,F 两点作直线。
则直线 EF 就是线段 AB 的垂直平分线.
1
2
( 为什么?)
画弧交于E,F.
A
B
E
F
通过尺规作图作线段的垂直平分线
新知
如图,在线段AB的垂直平分线l上,分别取一些点P1,P2,P3……分别量一量P1、P2、P3到点A与点B的距离,你会有什么发现?
:线段垂直平分线上的点到线段两端的距离_______。
发现:
相等
探究
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
……
=
=
=
猜想
猜想:线段垂直平分线上的点到线段两端的距离相等。
A
M
P
B
O
已知:如图,直线 MN 是线段 AB 的垂直平分线, P 是 MN 上任意一点 .
求证:PA =PB.
当P不与O重合时,可以通过证明△AOP ≌ △BOP,得到PA =PB
探究
N
分析:
P
A
B
M
O
N
证明:
∵ MN⊥AB
∴ AO=OB
在 AOP和 BOP 中,
AO=OB
∠AOP= ∠BOP
PO=PO
∴ AOP ≌ BOP
∴ PA=PB
∵
(SAS)
(垂直的定义)
(已证)
(已证)
(公共边)
(全等三角形的对应边相等)
∵ MN是线段 AB 的垂直平分线
∴ ∠AOP= ∠BOP=90
1、当P与O重合时,显然PA=PB
2、当P不与O重合时,
条件:
点在线段的垂直平分线上.
结论:
这个点到线段两端点的距离相等.
N
线段的垂直平分线的性质定理:
线段的垂直平分线上的点到线段两端的距离相等。
符号语言:
∵ MN⊥AB于O,OA=OB
(或者说MN是线段AB的垂直平分线)
∴ ____=_____
M
B
P
A
O
新知
PA
PB
1、完成填空并说明理由。
如图:已知直线l垂直平分线段AB,P是l上一点,若PA=1,
则PB=______
P
A
B
l
C
练习
理由:_______________________________________________________________
2、如图,在 ABC 中,AB边 的垂直平分线 DE 分别交 AB,AC 于点 E,D.
(1)BD+CD与AC的长有什么关系?
例题
2、如图,在 ABC 中,DE是边AB 的垂直平分线 ,分别 交 AB,AC 于点 E,D.
(2)若BC=8,AC=10,则 BCD周长为多少?
例题
收获
当线段的垂直平分线和三角形的周长同时出现时,可以借助垂直平分线的性质,将三角形中某两边的和等量代换成一条边的长,进而借助整体的思想求解相关问题。
变式
1、如图所示,在 △ABC 中,AB,AC 的垂直平分线分别交BC 于 D,E,垂足分别是 M,N.
若 ADE的周长是10,则BC的长为多少?
小结
1、运用尺规作图,作线段的垂直平分线的方法。
A
B
E
F
2、线段的垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等。
P
A
B
l
C
作业
基础巩固;课本P131,习题15.2第2题
拓展提高:课本P131,习题15.2第4题
自主探究:
1、预习课本P129-130内容
2、思考:你能写出线段垂直平分线性质定理的逆命题吗?它是真命题吗?
