13.2.2 三角形的中线、角平分线、高 教案 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 13.2.2 三角形的中线、角平分线、高 教案 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 42.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 17:28:19 | ||
图片预览

文档简介
13.2.2 三角形的中线、角平分线、高
◇教学目标◇
1.了解三角形的中线、角平分线、高的概念.
2.让学生经历画三角形的中线、角平分线、高的过程,理解三角形的中线、角平分线、高的特点以及符号语言和图形语言的表达方法.
3.会用工具准确画出三角形的中线、角平分线、高.
4.培养学生观察、分析、作图、解决问题的能力.
5.培养学生敢于实践操作、勇于发现、大胆探索、合作创新的精神.
◇教学重难点◇
教学重点
三角形的中线、角平分线、高线的概念及画法.
教学难点
探究三角形的三条高线、三条角平分线、三条中线都交于一点的过程.
◇教学过程◇
一、情境导入
有一块三角形的地,小明的爸爸想种花草,妈妈想种菜.于是想平分三角形的面积,一半种花草,一半种菜,不知如何做,小明说,这还不好办,作一边的中线就行了,聪明的你,能帮他们家把这块地分成面积相等的两部分吗?知道小明这样做的原因吗?
二、合作探究
探究点1 三角形的中线
典例1 三角形一边上的中线把原三角形分成两个 ( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
[解析] 根据三角形的面积公式以及三角形的中线定义,可知三角形一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.
[答案] B
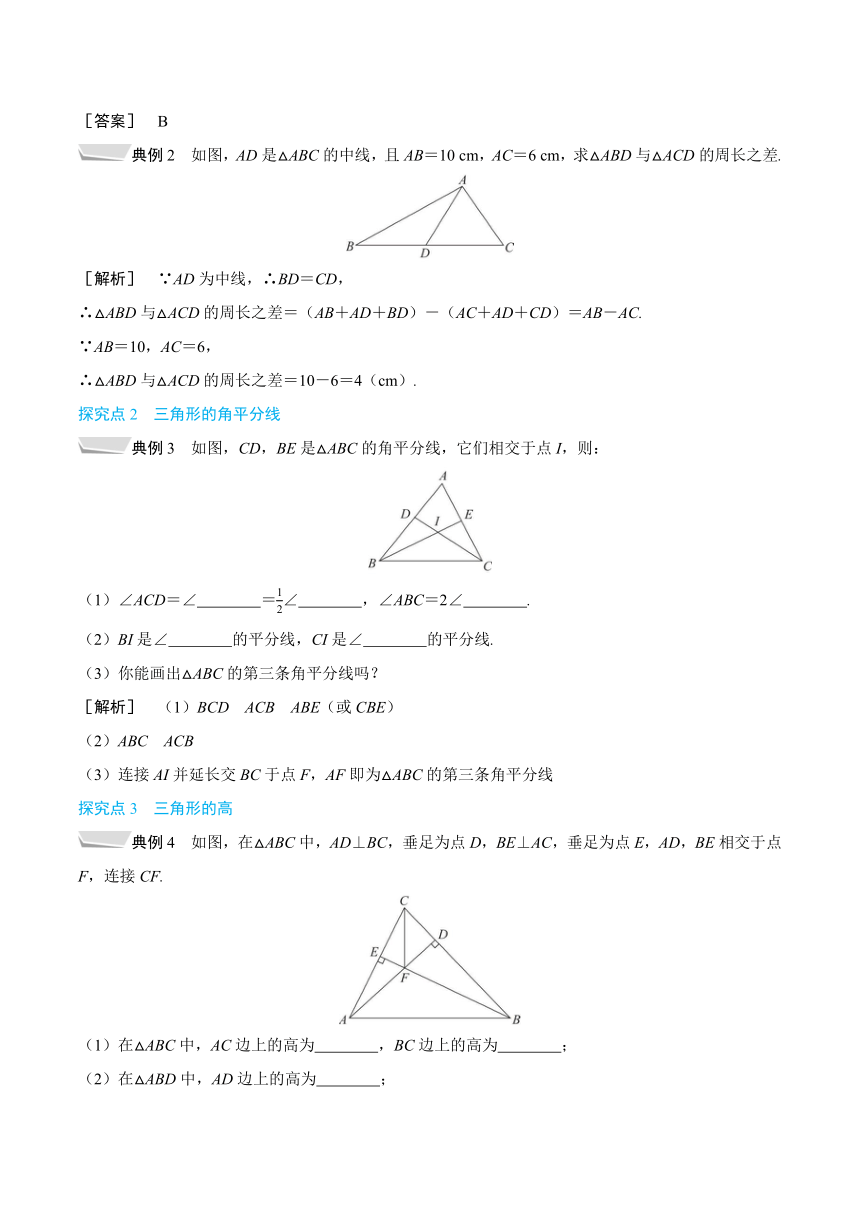
典例2 如图,AD是△ABC的中线,且AB=10 cm,AC=6 cm,求△ABD与△ACD的周长之差.
[解析] ∵AD为中线,∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)-(AC+AD+CD)=AB-AC.
∵AB=10,AC=6,
∴△ABD与△ACD的周长之差=10-6=4(cm).
探究点2 三角形的角平分线
典例3 如图,CD,BE是△ABC的角平分线,它们相交于点I,则:
(1)∠ACD=∠ =∠ ,∠ABC=2∠ .
(2)BI是∠ 的平分线,CI是∠ 的平分线.
(3)你能画出△ABC的第三条角平分线吗?
[解析] (1)BCD ACB ABE(或CBE)
(2)ABC ACB
(3)连接AI并延长交BC于点F,AF即为△ABC的第三条角平分线
探究点3 三角形的高
典例4 如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD,BE相交于点F,连接CF.
(1)在△ABC中,AC边上的高为 ,BC边上的高为 ;
(2)在△ABD中,AD边上的高为 ;
(3)在△BCE中,CE边上的高为 ;
(4)在△BCF中,BC边上的高为 ;
(5)在△ABF中,AF边上的高为 ,BF边上的高为 .
[解析] 三角形的高即从三角形的一个顶点向它的对边所在直线引垂线,顶点和垂足间的线段.
[答案] (1)BE AD (2)BD (3)BE
(4)FD (5)BD AE
三、板书设计
三角形的中线、角平分线、高
三角形的中线、
角平分线、高
◇教学反思◇
通过本课时的教学要让学生认识三角形的三条重要线段的概念、图形和它们的相关特性,如三角形的中线把三角形分为面积相等的两部分,三角形的三条高线、三条中线、三条角平分线都相交于一点的性质,应逐步加强学生几何语言的表达能力.
◇教学目标◇
1.了解三角形的中线、角平分线、高的概念.
2.让学生经历画三角形的中线、角平分线、高的过程,理解三角形的中线、角平分线、高的特点以及符号语言和图形语言的表达方法.
3.会用工具准确画出三角形的中线、角平分线、高.
4.培养学生观察、分析、作图、解决问题的能力.
5.培养学生敢于实践操作、勇于发现、大胆探索、合作创新的精神.
◇教学重难点◇
教学重点
三角形的中线、角平分线、高线的概念及画法.
教学难点
探究三角形的三条高线、三条角平分线、三条中线都交于一点的过程.
◇教学过程◇
一、情境导入
有一块三角形的地,小明的爸爸想种花草,妈妈想种菜.于是想平分三角形的面积,一半种花草,一半种菜,不知如何做,小明说,这还不好办,作一边的中线就行了,聪明的你,能帮他们家把这块地分成面积相等的两部分吗?知道小明这样做的原因吗?
二、合作探究
探究点1 三角形的中线
典例1 三角形一边上的中线把原三角形分成两个 ( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
[解析] 根据三角形的面积公式以及三角形的中线定义,可知三角形一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.
[答案] B
典例2 如图,AD是△ABC的中线,且AB=10 cm,AC=6 cm,求△ABD与△ACD的周长之差.
[解析] ∵AD为中线,∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)-(AC+AD+CD)=AB-AC.
∵AB=10,AC=6,
∴△ABD与△ACD的周长之差=10-6=4(cm).
探究点2 三角形的角平分线
典例3 如图,CD,BE是△ABC的角平分线,它们相交于点I,则:
(1)∠ACD=∠ =∠ ,∠ABC=2∠ .
(2)BI是∠ 的平分线,CI是∠ 的平分线.
(3)你能画出△ABC的第三条角平分线吗?
[解析] (1)BCD ACB ABE(或CBE)
(2)ABC ACB
(3)连接AI并延长交BC于点F,AF即为△ABC的第三条角平分线
探究点3 三角形的高
典例4 如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,AD,BE相交于点F,连接CF.
(1)在△ABC中,AC边上的高为 ,BC边上的高为 ;
(2)在△ABD中,AD边上的高为 ;
(3)在△BCE中,CE边上的高为 ;
(4)在△BCF中,BC边上的高为 ;
(5)在△ABF中,AF边上的高为 ,BF边上的高为 .
[解析] 三角形的高即从三角形的一个顶点向它的对边所在直线引垂线,顶点和垂足间的线段.
[答案] (1)BE AD (2)BD (3)BE
(4)FD (5)BD AE
三、板书设计
三角形的中线、角平分线、高
三角形的中线、
角平分线、高
◇教学反思◇
通过本课时的教学要让学生认识三角形的三条重要线段的概念、图形和它们的相关特性,如三角形的中线把三角形分为面积相等的两部分,三角形的三条高线、三条中线、三条角平分线都相交于一点的性质,应逐步加强学生几何语言的表达能力.
同课章节目录
