14.1 全等三角形及其性质 教案 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.1 全等三角形及其性质 教案 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 61.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-15 13:41:01 | ||
图片预览

文档简介
第十四章 全等三角形
14.1 全等三角形及其性质
◇教学目标◇
1.掌握全等形、全等三角形的概念,能应用符号语言表示两个三角形全等.
2.能熟练地找出两个全等三角形的对应元素.
3.掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题.
4.联系学生的生活环境,创设情景,使学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣.
◇教学重难点◇
教学重点
全等三角形的性质及其应用.
教学难点
能正确地识别全等三角形的对应元素.
◇教学过程◇
一、情境导入
观察下面这些图形,它们能够完全重合吗?
二、合作探究
探究点1 全等形的概念
典例1 下列四组图形中,是全等形的一组是 ( )
[解析] 观察图形的特点可发现:A,B,C中的两个图形大小不同,D则完全相同.
[答案] D
探究点2 全等三角形的概念
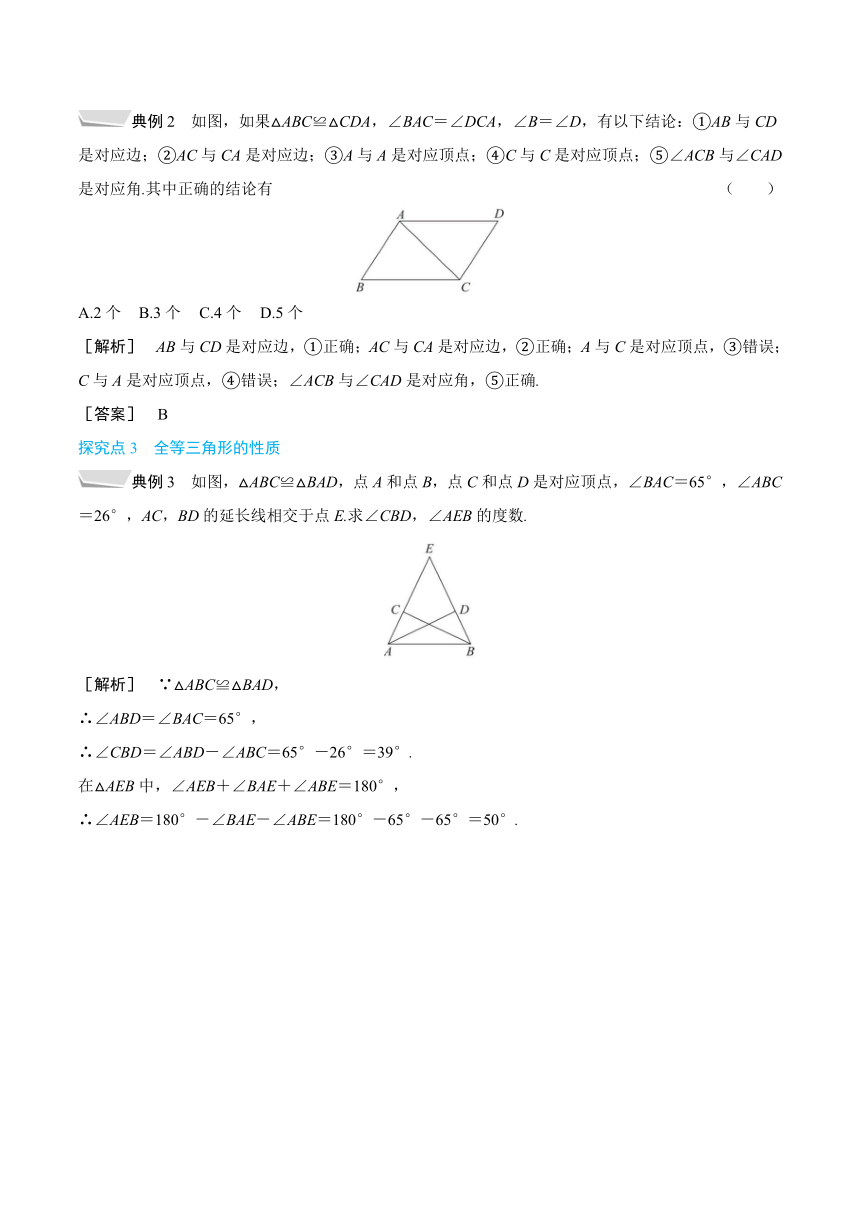
典例2 如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,有以下结论:①AB与CD是对应边;②AC与CA是对应边;③A与A是对应顶点;④C与C是对应顶点;⑤∠ACB与∠CAD是对应角.其中正确的结论有 ( )
A.2个 B.3个 C.4个 D.5个
[解析] AB与CD是对应边,①正确;AC与CA是对应边,②正确;A与C是对应顶点,③错误;C与A是对应顶点,④错误;∠ACB与∠CAD是对应角,⑤正确.
[答案] B
探究点3 全等三角形的性质
典例3 如图,△ABC≌△BAD,点A和点B,点C和点D是对应顶点,∠BAC=65°,∠ABC=26°,AC,BD的延长线相交于点E.求∠CBD,∠AEB的度数.
[解析] ∵△ABC≌△BAD,
∴∠ABD=∠BAC=65°,
∴∠CBD=∠ABD-∠ABC=65°-26°=39°.
在△AEB中,∠AEB+∠BAE+∠ABE=180°,
∴∠AEB=180°-∠BAE-∠ABE=180°-65°-65°=50°.
探究点4 利用全等三角形的性质解决问题
典例4 如图所示,△ABD≌△ACD,∠BAC=90°.
(1)求∠B的大小;
(2)判断AD与BC的位置关系,并说明理由.
[解析] (1)∵△ABD≌△ACD,
∴∠B=∠C.
又∵∠BAC=90°,∴∠B=∠C=45°.
(2)AD⊥BC.
理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA.
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,∴AD⊥BC.
三、板书设计
全等三角形及其性质
全等三角形
◇教学反思◇
由于学生学习平面几何的时间不长,识图能力还比较薄弱,学生的思维依赖于具体的直观形象,在教学时借助几何画板演示图形的形成与变换,来帮助学生更好地发现理解图形的特征,尤其对于较复杂的几何图形中的对应边、对应角,方便学生迅速地找出,简化难点.
14.1 全等三角形及其性质
◇教学目标◇
1.掌握全等形、全等三角形的概念,能应用符号语言表示两个三角形全等.
2.能熟练地找出两个全等三角形的对应元素.
3.掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题.
4.联系学生的生活环境,创设情景,使学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣.
◇教学重难点◇
教学重点
全等三角形的性质及其应用.
教学难点
能正确地识别全等三角形的对应元素.
◇教学过程◇
一、情境导入
观察下面这些图形,它们能够完全重合吗?
二、合作探究
探究点1 全等形的概念
典例1 下列四组图形中,是全等形的一组是 ( )
[解析] 观察图形的特点可发现:A,B,C中的两个图形大小不同,D则完全相同.
[答案] D
探究点2 全等三角形的概念
典例2 如图,如果△ABC≌△CDA,∠BAC=∠DCA,∠B=∠D,有以下结论:①AB与CD是对应边;②AC与CA是对应边;③A与A是对应顶点;④C与C是对应顶点;⑤∠ACB与∠CAD是对应角.其中正确的结论有 ( )
A.2个 B.3个 C.4个 D.5个
[解析] AB与CD是对应边,①正确;AC与CA是对应边,②正确;A与C是对应顶点,③错误;C与A是对应顶点,④错误;∠ACB与∠CAD是对应角,⑤正确.
[答案] B
探究点3 全等三角形的性质
典例3 如图,△ABC≌△BAD,点A和点B,点C和点D是对应顶点,∠BAC=65°,∠ABC=26°,AC,BD的延长线相交于点E.求∠CBD,∠AEB的度数.
[解析] ∵△ABC≌△BAD,
∴∠ABD=∠BAC=65°,
∴∠CBD=∠ABD-∠ABC=65°-26°=39°.
在△AEB中,∠AEB+∠BAE+∠ABE=180°,
∴∠AEB=180°-∠BAE-∠ABE=180°-65°-65°=50°.
探究点4 利用全等三角形的性质解决问题
典例4 如图所示,△ABD≌△ACD,∠BAC=90°.
(1)求∠B的大小;
(2)判断AD与BC的位置关系,并说明理由.
[解析] (1)∵△ABD≌△ACD,
∴∠B=∠C.
又∵∠BAC=90°,∴∠B=∠C=45°.
(2)AD⊥BC.
理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA.
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,∴AD⊥BC.
三、板书设计
全等三角形及其性质
全等三角形
◇教学反思◇
由于学生学习平面几何的时间不长,识图能力还比较薄弱,学生的思维依赖于具体的直观形象,在教学时借助几何画板演示图形的形成与变换,来帮助学生更好地发现理解图形的特征,尤其对于较复杂的几何图形中的对应边、对应角,方便学生迅速地找出,简化难点.
同课章节目录
