14.2 第4课时 利用斜边、直角边判定直角三角形全等(HL)教案 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.2 第4课时 利用斜边、直角边判定直角三角形全等(HL)教案 2025-2026学年数学人教版八年级上册 | 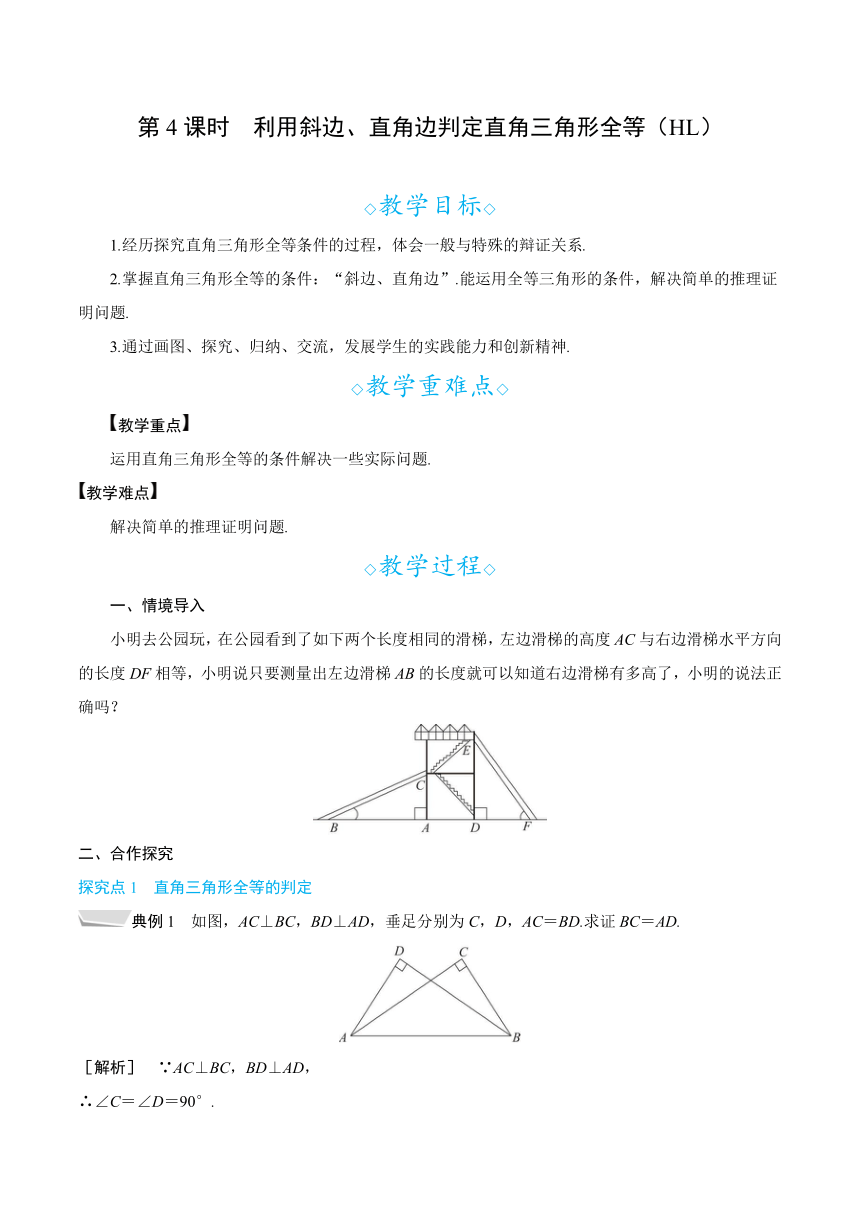 | |
| 格式 | docx | ||
| 文件大小 | 48.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 17:29:34 | ||
图片预览

文档简介
第4课时 利用斜边、直角边判定直角三角形全等(HL)
◇教学目标◇
1.经历探究直角三角形全等条件的过程,体会一般与特殊的辩证关系.
2.掌握直角三角形全等的条件:“斜边、直角边”.能运用全等三角形的条件,解决简单的推理证明问题.
3.通过画图、探究、归纳、交流,发展学生的实践能力和创新精神.
◇教学重难点◇
教学重点
运用直角三角形全等的条件解决一些实际问题.
教学难点
解决简单的推理证明问题.
◇教学过程◇
一、情境导入
小明去公园玩,在公园看到了如下两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,小明说只要测量出左边滑梯AB的长度就可以知道右边滑梯有多高了,小明的说法正确吗?
二、合作探究
探究点1 直角三角形全等的判定
典例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证BC=AD.
[解析] ∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD.
探究点2 HL的应用
典例2 如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.求证:△ACF≌△BDE.
[解析] ∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°.
在Rt△ACE和Rt△BDF中,
∴Rt△ACE≌Rt△BDF(HL),
∴∠A=∠B.
∵AE=BF,
∴AE-EF=BF-EF,即AF=BE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
探究点3 三角形全等判定的综合应用
典例3 如图,在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,点E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明理由.
[解析] BF⊥AE.
理由:∵∠ACB=90°,∴∠ACE=∠BCD=90°.
又∵BC=AC,BD=AE,
∴△BDC≌△AEC(HL),∴∠CBD=∠CAE.
又∵∠CAE+∠E=90°,
∴∠EBF+∠E=90°,
∴∠BFE=90°,即BF⊥AE.
三、板书设计
利用斜边、直角边判定直角三角形全等(HL)
直角三角形
全等的判定
◇教学反思◇
本节的内容是直角三角形全等的判定方法,主要让学生在回顾全等三角形判定的基础上,进一步研究直角三角形全等的判定的方法,让学生充分认识特殊与一般的关系,加深他们对公理的多层次的理解.
◇教学目标◇
1.经历探究直角三角形全等条件的过程,体会一般与特殊的辩证关系.
2.掌握直角三角形全等的条件:“斜边、直角边”.能运用全等三角形的条件,解决简单的推理证明问题.
3.通过画图、探究、归纳、交流,发展学生的实践能力和创新精神.
◇教学重难点◇
教学重点
运用直角三角形全等的条件解决一些实际问题.
教学难点
解决简单的推理证明问题.
◇教学过程◇
一、情境导入
小明去公园玩,在公园看到了如下两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,小明说只要测量出左边滑梯AB的长度就可以知道右边滑梯有多高了,小明的说法正确吗?
二、合作探究
探究点1 直角三角形全等的判定
典例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证BC=AD.
[解析] ∵AC⊥BC,BD⊥AD,
∴∠C=∠D=90°.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD.
探究点2 HL的应用
典例2 如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.求证:△ACF≌△BDE.
[解析] ∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°.
在Rt△ACE和Rt△BDF中,
∴Rt△ACE≌Rt△BDF(HL),
∴∠A=∠B.
∵AE=BF,
∴AE-EF=BF-EF,即AF=BE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
探究点3 三角形全等判定的综合应用
典例3 如图,在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,点E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明理由.
[解析] BF⊥AE.
理由:∵∠ACB=90°,∴∠ACE=∠BCD=90°.
又∵BC=AC,BD=AE,
∴△BDC≌△AEC(HL),∴∠CBD=∠CAE.
又∵∠CAE+∠E=90°,
∴∠EBF+∠E=90°,
∴∠BFE=90°,即BF⊥AE.
三、板书设计
利用斜边、直角边判定直角三角形全等(HL)
直角三角形
全等的判定
◇教学反思◇
本节的内容是直角三角形全等的判定方法,主要让学生在回顾全等三角形判定的基础上,进一步研究直角三角形全等的判定的方法,让学生充分认识特殊与一般的关系,加深他们对公理的多层次的理解.
同课章节目录
