5.1 总体平均数与方差的估计 同步练习(含答案)
文档属性
| 名称 | 5.1 总体平均数与方差的估计 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 335.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.1 总体平均数与方差的估计
一、单选题
1.(2021八下·辛集期末)若某一样本的方差为,样本容量为5.则下列说法:①当时,;②该样本的平均数为7;③x,y的平均数是7;④该样本的方差与x,y的值无关.其中不正确的是( )
A.①② B.②④ C.①③ D.③④
2.(2025·涪城模拟)学校新组建的篮球队12名队员的年龄如下表所示:
年龄/岁 13 14 15 16
人数 5 4 1 2
则这12名队员年龄的众数和平均数分别是( )
A.13,14 B.14,14 C.13,14.5 D.14,14.5
3.(2024八下·兴业期末)某同学对数据32,36,28,33,4■,43,50进行统计分析,发现两位数“4■”的个位数字模糊不清,则下列统计量不受影响的是( )
A.平均数 B.众数 C.中位数 D.方差
4.(2023八下·涪陵期末)在期末考试中,初二某班级有1组、2组、3组、4组共四个组,每个组学生的数学成绩的平均分相等,方差分别为,,,,则该班这四个组的学生期末数学成绩波动最小的是( )
A.1组 B.2组 C.3组 D.4组
5.(2021八下·重庆期末)数据 ,0,3,4,5的平均数是( )
A.4 B.3 C.2 D.1
6.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
A.众数是35 B.中位数是34
C.平均数是35 D.方差是6
7.(2024·天河模拟)某次射击训练中,甲、乙、丙、丁四名运动员10次射击成绩的平均数(单位:环)与方差如右表所示.根据表中数据,这四人中成绩好且发挥稳定的是( )
甲 乙 丙 丁
9 8 9 9
A.甲 B.乙 C.丙 D.丁
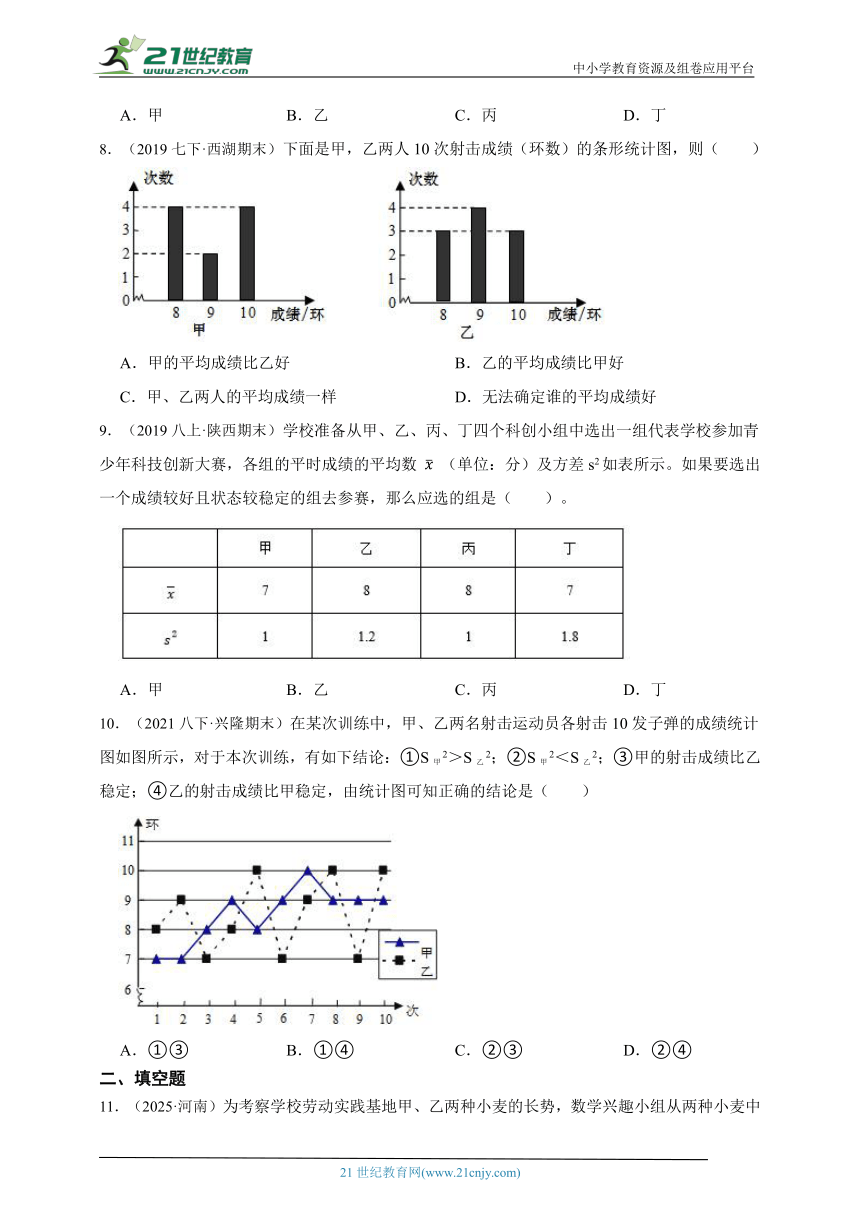
8.(2019七下·西湖期末)下面是甲,乙两人10次射击成绩(环数)的条形统计图,则( )
A.甲的平均成绩比乙好 B.乙的平均成绩比甲好
C.甲、乙两人的平均成绩一样 D.无法确定谁的平均成绩好
9.(2019八上·陕西期末)学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差s2如表所示。如果要选出一个成绩较好且状态较稳定的组去参赛,那么应选的组是( )。
A.甲 B.乙 C.丙 D.丁
10.(2021八下·兴隆期末)在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
A.①③ B.①④ C.②③ D.②④
二、填空题
11.(2025·河南)为考察学校劳动实践基地甲、乙两种小麦的长势,数学兴趣小组从两种小麦中各随机抽取20株进行测量,测得两种小麦苗高的平均数相同,方差分别为,则这两种小麦长势更整齐的是 (填“甲”或“乙”).
12.(2024八下·丰都县期末)某5人学习小组在某次测试中,成绩(分)分别为:86,88,91,91,94,方差,后来老师发现每人都少加了2分,每人补加2分后,这5人新成绩的方差 .
13.(2023九上·栾城期中)“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:kg/亩,,kg/亩,,则品种 更适合在该村推广.(填“甲”或“乙”)
14.(2024九上·崂山开学考)某校体育期末考核“仰卧起坐”和“米”两项,并按的比例算出期末成绩.已知小林这两项的考试成绩分别为分、分,则小林的体育期末成绩为 分.
15.(2024八上·武侯期末)某公司招聘职员,公司对应聘者进行了面试和笔试(满分均为100分),规定笔试成绩占60%,面试成绩占40%,应聘者张华的笔试成绩和面试成绩分别为95分和90分,她的最终得分是 分.
16.(2021八下·鄞州期中)如果一组按从小到大排序的数据a,b,c的平均数是b,方差是S2,那么数据a+99,b+100,c+101的方差将 S2(填“大于”“小于”或“等于”).
三、计算题
17.(2022八下·平坝期末)为弘扬平坝民间文化艺术,我区某校举办了“屯堡地戏诗文大赛”活动,小学部、初中部根据初赛成绩,各选出5名选手组成小学代表队和初中代表队参加学校决赛.两个代表队各选出的5名选手的决赛成绩如图所示.
众数 中位数 平均数
小学代表队 a 85 c
初中代表队 100 b 85
(1)表格中,______ ,______ ,______ ;
(2)计算两队决赛成绩的方差,并判断哪一个代表队的选手的成绩较为稳定.
18.(2023九下·雄县月考)某市中考体育必考科目是长跑(男生1000米,女生800米);抽考科目有4项[50米、立定和跳远、跳绳、男生引体向上或实心球(女生仰卧起坐或实心球)];选考科目有足球、篮球和排球,每个考生任选一项作为选考考试项目.嘉嘉和淇淇在中考体育中各项成绩(每一项满分10分的)条形统计图如图所示.
(1)分别求出嘉嘉和淇淇的成绩之和,并说明他们两个谁更优秀;
(2)如果中考体育长跑,抽考科目、选考科目按照6∶5∶4的比例计算成绩,分别计算他们的中考体育综合成绩,并判断(1)中的结果是否会改变.
四、解答题
19.(2024九上·西塘月考)在引体向上项目中,某校初三名男生考试成绩如下列所示:
成绩(单位:次)
人数
(1)分别求这些男生成绩的众数、中位数与平均数;
(2)规定次以上(含次)为优秀,这所学校男生此项目考试成绩的优秀率是多少?
20.(2023八下·惠安期末)为更好地开展劳动教育,某校随机调查了100名学生目前每周劳动时间(单位:小时)作为样本,收集并整理数据如下表.
学生目前每周劳动时间统计表
每周劳动时间(小时)
人数(人) 30 19 18 12
(1)写出表中__________;画扇形统计图时,这组数据对应的扇形圆心角是__________度.
(2)求该校学生目前每周劳动时间的样本平均数.
21.(2016·柳州)在一次“社会主义核心价值观”知识竞赛中,四个小组回答正确题数情况如图,求这四个小组回答正确题数的平均数.
22.已知一组数据:x,10,12,6的中位数与平均数相等,求x的值。
答案解析部分
1.【答案】D
【知识点】方差
2.【答案】A
【知识点】平均数及其计算;众数
3.【答案】C
【知识点】平均数及其计算;中位数;方差;众数
4.【答案】A
【知识点】方差
5.【答案】C
【知识点】平均数及其计算
6.【答案】B
【知识点】加权平均数及其计算;方差
7.【答案】D
【知识点】平均数及其计算;方差
8.【答案】C
【知识点】条形统计图;平均数及其计算
9.【答案】C
【知识点】平均数及其计算;方差
10.【答案】C
【知识点】折线统计图;方差
11.【答案】甲
【知识点】方差;分析数据的波动程度
12.【答案】
【知识点】方差
13.【答案】乙
【知识点】方差
14.【答案】87
【知识点】加权平均数及其计算
15.【答案】93
【知识点】加权平均数及其计算
16.【答案】大于
【知识点】平均数及其计算;方差
17.【答案】(1)85,80,85
(2)小学代表队:70,初中代表队:160,小学代表队的成绩较为稳定
【知识点】平均数及其计算;中位数;方差;众数
18.【答案】(1)两人一样优秀
(2)嘉嘉的成绩更优秀,(1)中的结果会改变
【知识点】条形统计图;加权平均数及其计算
19.【答案】(1)10,,
(2)
【知识点】平均数及其计算;中位数;众数
20.【答案】(1);108°
(2)2.7小时
【知识点】扇形统计图;加权平均数及其计算
21.【答案】解:(6+12+16+10)÷4
=44÷4
=11
∴这四个小组回答正确题数的平均数是11
【知识点】条形统计图;加权平均数及其计算
22.【答案】解:当时,这组数据按从小到大顺序排列为x,6,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,x,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,10,x,12
由题意得
则(舍)
当时,这组数据按从小到大顺序排列为6,10,12,x
由题意得
则
综上所述:x=4或8或16.
【知识点】平均数及其计算;中位数
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1 总体平均数与方差的估计
一、单选题
1.(2021八下·辛集期末)若某一样本的方差为,样本容量为5.则下列说法:①当时,;②该样本的平均数为7;③x,y的平均数是7;④该样本的方差与x,y的值无关.其中不正确的是( )
A.①② B.②④ C.①③ D.③④
2.(2025·涪城模拟)学校新组建的篮球队12名队员的年龄如下表所示:
年龄/岁 13 14 15 16
人数 5 4 1 2
则这12名队员年龄的众数和平均数分别是( )
A.13,14 B.14,14 C.13,14.5 D.14,14.5
3.(2024八下·兴业期末)某同学对数据32,36,28,33,4■,43,50进行统计分析,发现两位数“4■”的个位数字模糊不清,则下列统计量不受影响的是( )
A.平均数 B.众数 C.中位数 D.方差
4.(2023八下·涪陵期末)在期末考试中,初二某班级有1组、2组、3组、4组共四个组,每个组学生的数学成绩的平均分相等,方差分别为,,,,则该班这四个组的学生期末数学成绩波动最小的是( )
A.1组 B.2组 C.3组 D.4组
5.(2021八下·重庆期末)数据 ,0,3,4,5的平均数是( )
A.4 B.3 C.2 D.1
6.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
A.众数是35 B.中位数是34
C.平均数是35 D.方差是6
7.(2024·天河模拟)某次射击训练中,甲、乙、丙、丁四名运动员10次射击成绩的平均数(单位:环)与方差如右表所示.根据表中数据,这四人中成绩好且发挥稳定的是( )
甲 乙 丙 丁
9 8 9 9
A.甲 B.乙 C.丙 D.丁
8.(2019七下·西湖期末)下面是甲,乙两人10次射击成绩(环数)的条形统计图,则( )
A.甲的平均成绩比乙好 B.乙的平均成绩比甲好
C.甲、乙两人的平均成绩一样 D.无法确定谁的平均成绩好
9.(2019八上·陕西期末)学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差s2如表所示。如果要选出一个成绩较好且状态较稳定的组去参赛,那么应选的组是( )。
A.甲 B.乙 C.丙 D.丁
10.(2021八下·兴隆期末)在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
A.①③ B.①④ C.②③ D.②④
二、填空题
11.(2025·河南)为考察学校劳动实践基地甲、乙两种小麦的长势,数学兴趣小组从两种小麦中各随机抽取20株进行测量,测得两种小麦苗高的平均数相同,方差分别为,则这两种小麦长势更整齐的是 (填“甲”或“乙”).
12.(2024八下·丰都县期末)某5人学习小组在某次测试中,成绩(分)分别为:86,88,91,91,94,方差,后来老师发现每人都少加了2分,每人补加2分后,这5人新成绩的方差 .
13.(2023九上·栾城期中)“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:kg/亩,,kg/亩,,则品种 更适合在该村推广.(填“甲”或“乙”)
14.(2024九上·崂山开学考)某校体育期末考核“仰卧起坐”和“米”两项,并按的比例算出期末成绩.已知小林这两项的考试成绩分别为分、分,则小林的体育期末成绩为 分.
15.(2024八上·武侯期末)某公司招聘职员,公司对应聘者进行了面试和笔试(满分均为100分),规定笔试成绩占60%,面试成绩占40%,应聘者张华的笔试成绩和面试成绩分别为95分和90分,她的最终得分是 分.
16.(2021八下·鄞州期中)如果一组按从小到大排序的数据a,b,c的平均数是b,方差是S2,那么数据a+99,b+100,c+101的方差将 S2(填“大于”“小于”或“等于”).
三、计算题
17.(2022八下·平坝期末)为弘扬平坝民间文化艺术,我区某校举办了“屯堡地戏诗文大赛”活动,小学部、初中部根据初赛成绩,各选出5名选手组成小学代表队和初中代表队参加学校决赛.两个代表队各选出的5名选手的决赛成绩如图所示.
众数 中位数 平均数
小学代表队 a 85 c
初中代表队 100 b 85
(1)表格中,______ ,______ ,______ ;
(2)计算两队决赛成绩的方差,并判断哪一个代表队的选手的成绩较为稳定.
18.(2023九下·雄县月考)某市中考体育必考科目是长跑(男生1000米,女生800米);抽考科目有4项[50米、立定和跳远、跳绳、男生引体向上或实心球(女生仰卧起坐或实心球)];选考科目有足球、篮球和排球,每个考生任选一项作为选考考试项目.嘉嘉和淇淇在中考体育中各项成绩(每一项满分10分的)条形统计图如图所示.
(1)分别求出嘉嘉和淇淇的成绩之和,并说明他们两个谁更优秀;
(2)如果中考体育长跑,抽考科目、选考科目按照6∶5∶4的比例计算成绩,分别计算他们的中考体育综合成绩,并判断(1)中的结果是否会改变.
四、解答题
19.(2024九上·西塘月考)在引体向上项目中,某校初三名男生考试成绩如下列所示:
成绩(单位:次)
人数
(1)分别求这些男生成绩的众数、中位数与平均数;
(2)规定次以上(含次)为优秀,这所学校男生此项目考试成绩的优秀率是多少?
20.(2023八下·惠安期末)为更好地开展劳动教育,某校随机调查了100名学生目前每周劳动时间(单位:小时)作为样本,收集并整理数据如下表.
学生目前每周劳动时间统计表
每周劳动时间(小时)
人数(人) 30 19 18 12
(1)写出表中__________;画扇形统计图时,这组数据对应的扇形圆心角是__________度.
(2)求该校学生目前每周劳动时间的样本平均数.
21.(2016·柳州)在一次“社会主义核心价值观”知识竞赛中,四个小组回答正确题数情况如图,求这四个小组回答正确题数的平均数.
22.已知一组数据:x,10,12,6的中位数与平均数相等,求x的值。
答案解析部分
1.【答案】D
【知识点】方差
2.【答案】A
【知识点】平均数及其计算;众数
3.【答案】C
【知识点】平均数及其计算;中位数;方差;众数
4.【答案】A
【知识点】方差
5.【答案】C
【知识点】平均数及其计算
6.【答案】B
【知识点】加权平均数及其计算;方差
7.【答案】D
【知识点】平均数及其计算;方差
8.【答案】C
【知识点】条形统计图;平均数及其计算
9.【答案】C
【知识点】平均数及其计算;方差
10.【答案】C
【知识点】折线统计图;方差
11.【答案】甲
【知识点】方差;分析数据的波动程度
12.【答案】
【知识点】方差
13.【答案】乙
【知识点】方差
14.【答案】87
【知识点】加权平均数及其计算
15.【答案】93
【知识点】加权平均数及其计算
16.【答案】大于
【知识点】平均数及其计算;方差
17.【答案】(1)85,80,85
(2)小学代表队:70,初中代表队:160,小学代表队的成绩较为稳定
【知识点】平均数及其计算;中位数;方差;众数
18.【答案】(1)两人一样优秀
(2)嘉嘉的成绩更优秀,(1)中的结果会改变
【知识点】条形统计图;加权平均数及其计算
19.【答案】(1)10,,
(2)
【知识点】平均数及其计算;中位数;众数
20.【答案】(1);108°
(2)2.7小时
【知识点】扇形统计图;加权平均数及其计算
21.【答案】解:(6+12+16+10)÷4
=44÷4
=11
∴这四个小组回答正确题数的平均数是11
【知识点】条形统计图;加权平均数及其计算
22.【答案】解:当时,这组数据按从小到大顺序排列为x,6,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,x,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,10,x,12
由题意得
则(舍)
当时,这组数据按从小到大顺序排列为6,10,12,x
由题意得
则
综上所述:x=4或8或16.
【知识点】平均数及其计算;中位数
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
