5.2 统计的简单应用 同步练习(含答案)
文档属性
| 名称 | 5.2 统计的简单应用 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 445.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 05:21:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.2 统计的简单应用
一、单选题
1.小丽随机写了一串数 “ 123321112233 ”, 则出现数字“ 3 ”的频数是( )
A.3 B.4 C.5 D.6
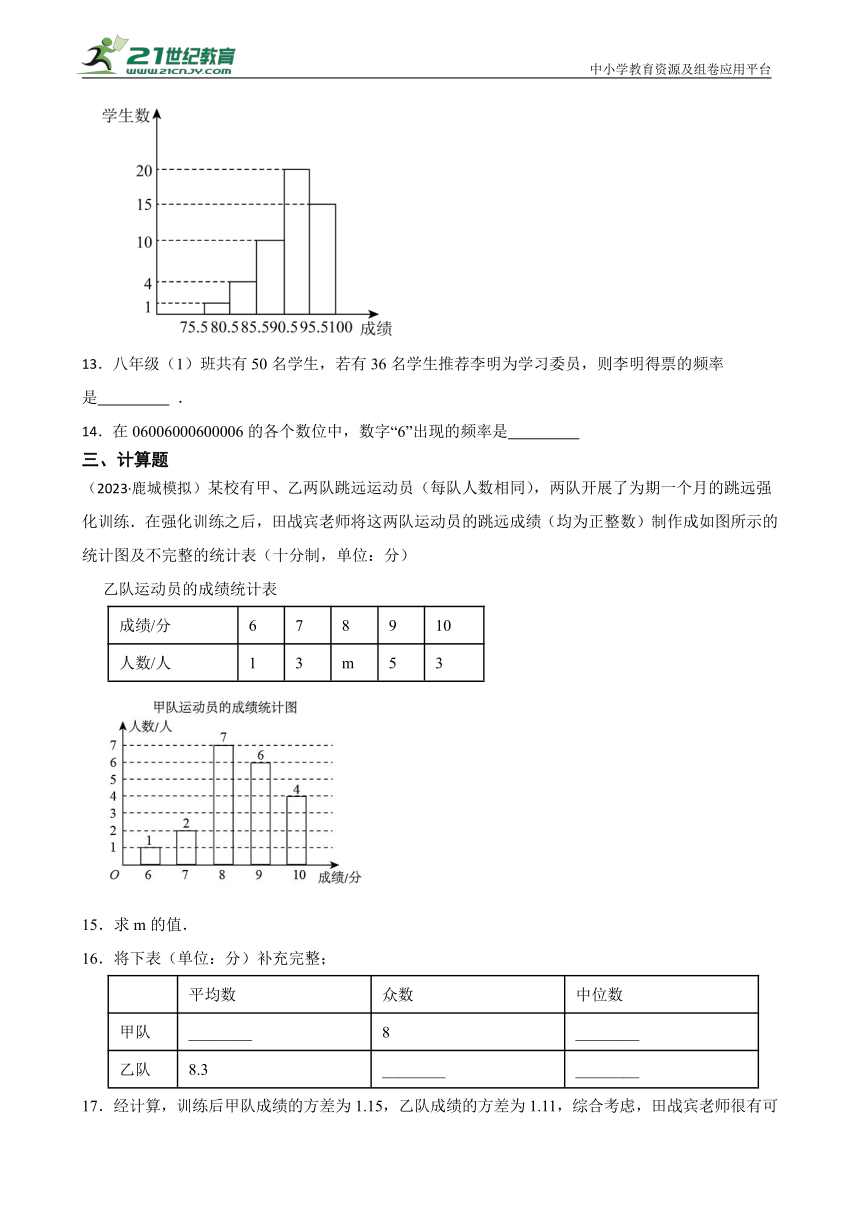
2.(2023七下·沙依巴克期末)某次数学测验,抽取部分同学的成绩(得分为整数),整理并绘制成如图所示的频数分布直方图,下列结论不正确的是( )
A.组距是10
B.抽取的学生有50人
C.成绩在60.5~70.5分的人数占抽取总人数的20%
D.优秀率(80分以上为优秀)在18%左右
3.(2020七下·武川期末)某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%、12%、40%、28%,第五组的频数是8,下列结论错误的是( )
A.该班有50名同学参赛 B.第五组的百分比为16%
C.成绩在70~80分的人数最多 D.80分以上的学生有14名
4.已知样本数据个数为30,且被分成4组,各组数据个数之比为2∶4∶3∶1,则第二小组和第三小组的频率分别为 ( )
A.0.4和0.3 B.0.4和9 C.12和0.3 D.12和9
5.(2023八下·双牌期末)在一个不透明的布袋中,红色、黑色、白色的小球共个,除颜色不同外其他完全相同,通过多次摸球试验后,摸到红色球、黑色球的频率分别稳定在和,则口袋中白色球的个数可能是( )
A. B. C. D.
6.已知一组数据有80个,其中最大值为143,最小值为50,取组距为10,则可分成( ).
A.10组 B.9组 C.8组 D.7组
7.(2019八下·淮安月考)某校八年级共有500名学生,为了了解这些学生的视力情况,随机抽査了40名学生的视力,对所得数据进行整理.若数据在4.8~5.0这一小组的频率为0.4,则可估计该校八年级学生视力在4.8~5.0范围内的人数有( )
A.300 B.200 C.150 D.16
8.(2015八下·杭州期中)如图是某学校全体教职工年龄的频数分布直方图(每组年龄包含最小值,不包含最大值),根据图形提供的信息,下列说法中错误的是( )
A.该学校教职工总人数是50人
B.这一组年龄在40≤x<42小组的教职工人数占该学校全体教职工总人数的20%
C.教职工年龄的中位数一定落在40≤x<42这一组
D.教职工年龄的众数一定在38≤x<40这一组
9.有40个数据,共分成6组,第1﹣4组的频数分别是10、5、7、6.第5组占10%,则第6组占( )
A.25% B.30% C.15% D.20%
二、填空题
10.(2019七下·武昌期末)已知10个数据:0,1,2,6,2,1,2,3,0,3,其中 2 出现的频数为 .
11.(2019七下·江汉期末)整理某个样本,其中最大值是24,最小值是2,取组距为3,则该样本可以分为 组.
12.(2024九下·浦东模拟)某校高一年级一班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),则成绩在90.5 95.5这一分数段的频率是
13.八年级(1)班共有50名学生,若有36名学生推荐李明为学习委员,则李明得票的频率是 .
14.在06006000600006的各个数位中,数字“6”出现的频率是
三、计算题
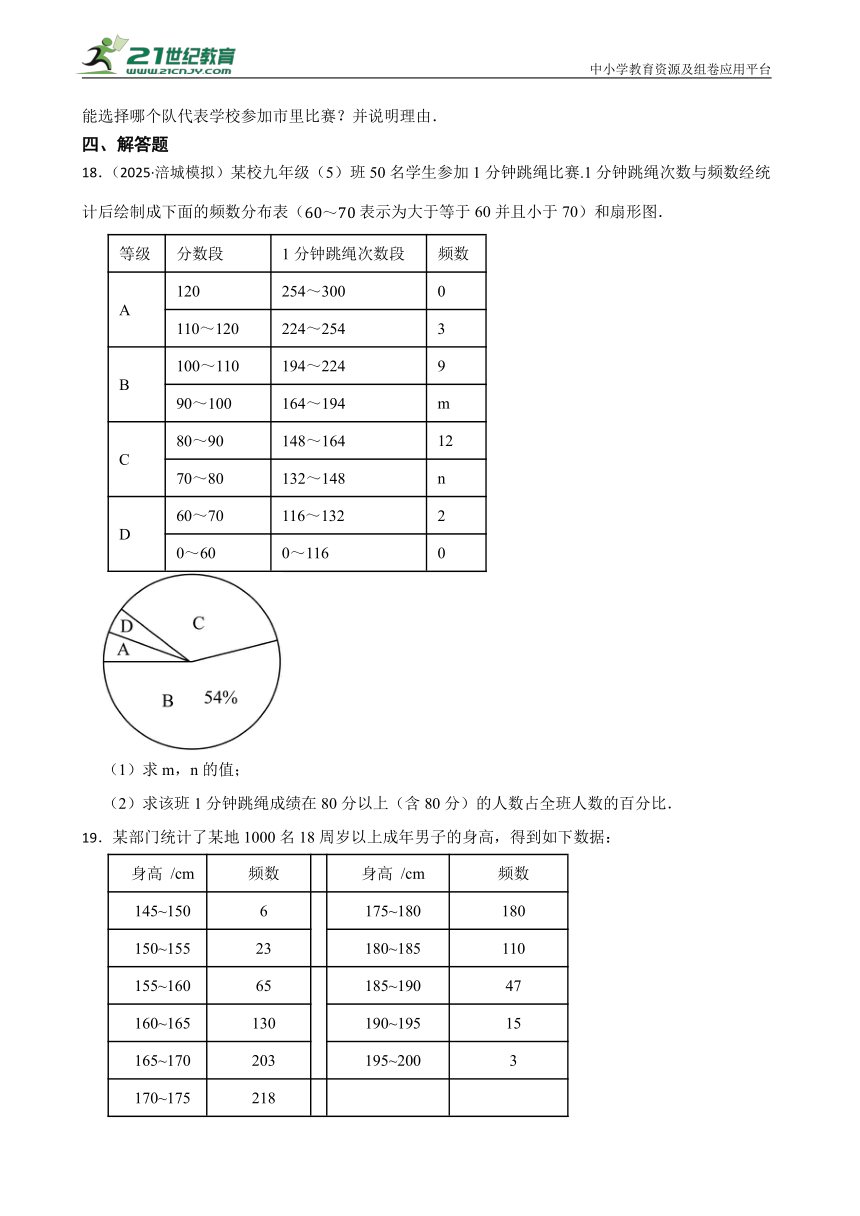
(2023·鹿城模拟)某校有甲、乙两队跳远运动员(每队人数相同),两队开展了为期一个月的跳远强化训练.在强化训练之后,田战宾老师将这两队运动员的跳远成绩(均为正整数)制作成如图所示的统计图及不完整的统计表(十分制,单位:分)
乙队运动员的成绩统计表
成绩/分 6 7 8 9 10
人数/人 1 3 m 5 3
15.求m的值.
16.将下表(单位:分)补充完整;
平均数 众数 中位数
甲队 ________ 8 ________
乙队 8.3 ________ ________
17.经计算,训练后甲队成绩的方差为1.15,乙队成绩的方差为1.11,综合考虑,田战宾老师很有可能选择哪个队代表学校参加市里比赛?并说明理由.
四、解答题
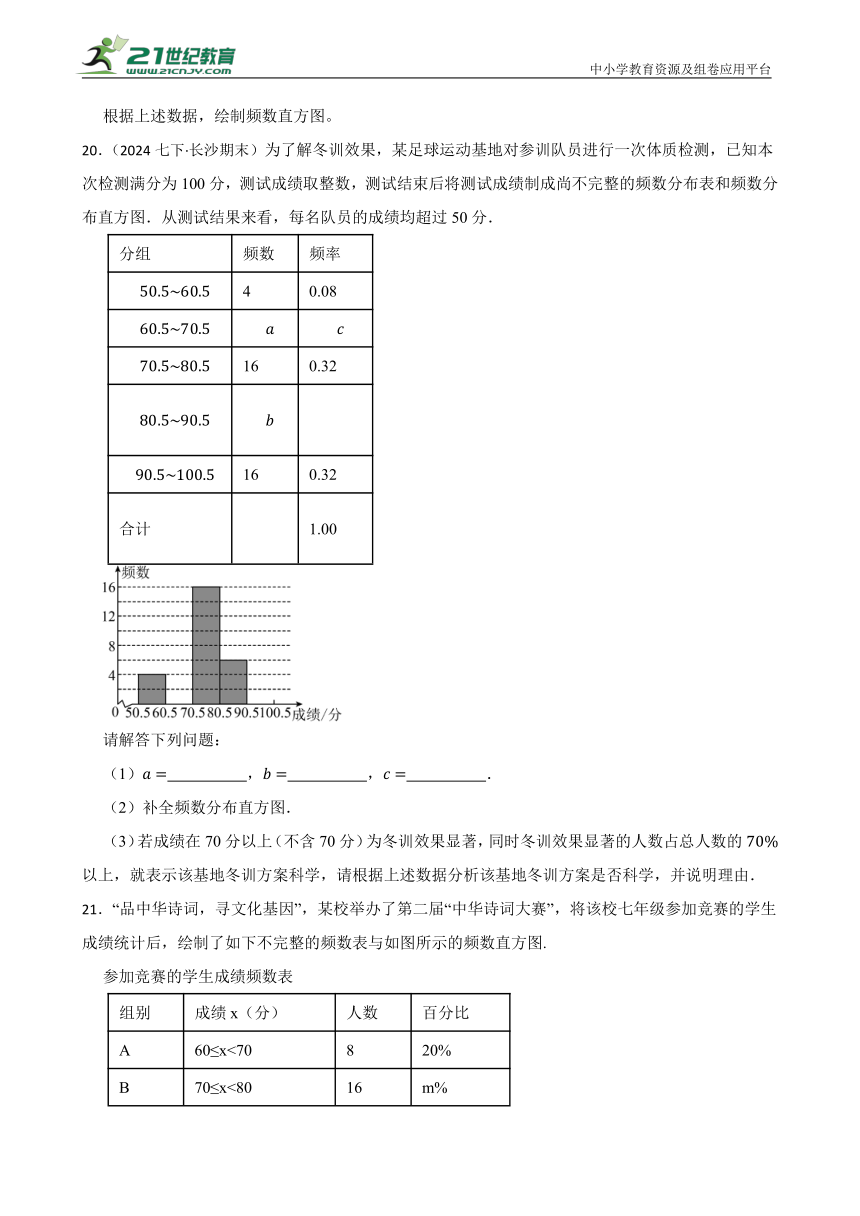
18.(2025·涪城模拟)某校九年级(5)班50名学生参加1分钟跳绳比赛.1分钟跳绳次数与频数经统计后绘制成下面的频数分布表(表示为大于等于60并且小于70)和扇形图.
等级 分数段 1分钟跳绳次数段 频数
A 120 254~300 0
110~120 224~254 3
B 100~110 194~224 9
90~100 164~194 m
C 80~90 148~164 12
70~80 132~148 n
D 60~70 116~132 2
0~60 0~116 0
(1)求m,n的值;
(2)求该班1分钟跳绳成绩在80分以上(含80分)的人数占全班人数的百分比.
19.某部门统计了某地1000名18周岁以上成年男子的身高,得到如下数据:
身高 /cm 频数 身高 /cm 频数
145~150 6 175~180 180
150~155 23 180~185 110
155~160 65 185~190 47
160~165 130 190~195 15
165~170 203 195~200 3
170~175 218
根据上述数据,绘制频数直方图。
20.(2024七下·长沙期末)为了解冬训效果,某足球运动基地对参训队员进行一次体质检测,已知本次检测满分为100分,测试成绩取整数,测试结束后将测试成绩制成尚不完整的频数分布表和频数分布直方图.从测试结果来看,每名队员的成绩均超过50分.
分组 频数 频率
4 0.08
16 0.32
16 0.32
合计
1.00
请解答下列问题:
(1) , , .
(2)补全频数分布直方图.
(3)若成绩在70分以上(不含70分)为冬训效果显著,同时冬训效果显著的人数占总人数的以上,就表示该基地冬训方案科学,请根据上述数据分析该基地冬训方案是否科学,并说明理由.
21.“品中华诗词,寻文化基因”,某校举办了第二届“中华诗词大赛”,将该校七年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数表与如图所示的频数直方图.
参加竞赛的学生成绩频数表
组别 成绩x(分) 人数 百分比
A 60≤x<70 8 20%
B 70≤x<80 16 m%
C 80≤x<90 a 30%
D 90≤x≤100 4 10%
参加竞赛的学生成绩频数直方图
解决下列问题:
(1)表中a= ,m= .
(2)补全频数直方图.
(3)方方参加了这次竞赛,成绩下来后,他对圆圆说:“我这次竞赛的成绩位于中游,比我答得好的人比比我答得差的人少3个.”请你算一算,方方是第几名?
答案解析部分
1.【答案】B
【知识点】频数与频率
2.【答案】D
【知识点】频数(率)分布直方图
3.【答案】D
【知识点】频数(率)分布直方图
4.【答案】A
【知识点】频数与频率;频数(率)分布表
5.【答案】C
【知识点】频数与频率
6.【答案】A
【知识点】频数(率)分布直方图
7.【答案】B
【知识点】频数与频率
8.【答案】D
【知识点】频数(率)分布直方图
9.【答案】D
【知识点】频数与频率
10.【答案】3
【知识点】频数与频率
11.【答案】8
【知识点】频数(率)分布表
12.【答案】0.4
【知识点】频数与频率;频数(率)分布直方图
13.【答案】0.72
【知识点】频数与频率
14.【答案】
【知识点】频数与频率
【答案】15.解:由题意得,甲队的人数为人,
∵甲乙两队人数相同,
∴乙队的人数为20人,
∴
16.解:甲队的平均数为:(6×1+7×2+8×7+9×6+10×4)÷(1+2+7+6+4)=170÷20=8.5(分),
∵甲队的成绩按从小到大排列,第10,11个成绩是8和9,
∴甲队的中位数是(8+9)÷2=8.5,
∵乙队成绩为8分的人数为7,人数最多,
∴乙队的众数是8,
∵乙队的成绩按从小到大排列,第10,11个成绩都是8,
∴乙队的中位数是(8+8)÷2=8,
故填表如下:
平均数 众数 中位数
甲队 8.5 8 8.5
乙队 8.3 8 8
17.解:田战宾老师很有可能会选择甲队作为学校代表参加市里比赛;理由如下:
∵甲、乙两队的方差相差不大,说明两队成绩整齐程度不相上下,但甲队的平均成绩较高,且甲队10分有4人,9分有6人,均比乙队多,
∴田战宾老师很有可能会选择甲队作为学校代表参加市里比赛.
【知识点】频数(率)分布直方图;加权平均数及其计算;中位数;众数
18.【答案】(1),
(2)
【知识点】频数(率)分布表;扇形统计图
19.【答案】解:频数直方图如图所示:
【知识点】频数(率)分布直方图
20.【答案】(1)8,6,0.16;
(2)解:补全频数分布直方图如下图所示:
(3)解:该基地冬训方案科学,理由如下:
由题意知70分以上的人数为:(人),
∵冬训效果显著的人数占总人数的百分比为:,
∴该基地冬训方案科学.
【知识点】频数(率)分布表;频数(率)分布直方图
21.【答案】(1)12;40
(2)解:80≤x<90频数为12,故高度为12,补全频数直方图如下:
(3)解:设比方方答得好的人为x人,则比方方答得差的人数为(x-3)人,
x+(x+3)+1=40,解得x=18;
故方方是第19名;
【知识点】一元二次方程的其他应用;频数(率)分布表;频数(率)分布直方图
5.2 统计的简单应用
一、单选题
1.小丽随机写了一串数 “ 123321112233 ”, 则出现数字“ 3 ”的频数是( )
A.3 B.4 C.5 D.6
2.(2023七下·沙依巴克期末)某次数学测验,抽取部分同学的成绩(得分为整数),整理并绘制成如图所示的频数分布直方图,下列结论不正确的是( )
A.组距是10
B.抽取的学生有50人
C.成绩在60.5~70.5分的人数占抽取总人数的20%
D.优秀率(80分以上为优秀)在18%左右
3.(2020七下·武川期末)某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%、12%、40%、28%,第五组的频数是8,下列结论错误的是( )
A.该班有50名同学参赛 B.第五组的百分比为16%
C.成绩在70~80分的人数最多 D.80分以上的学生有14名
4.已知样本数据个数为30,且被分成4组,各组数据个数之比为2∶4∶3∶1,则第二小组和第三小组的频率分别为 ( )
A.0.4和0.3 B.0.4和9 C.12和0.3 D.12和9
5.(2023八下·双牌期末)在一个不透明的布袋中,红色、黑色、白色的小球共个,除颜色不同外其他完全相同,通过多次摸球试验后,摸到红色球、黑色球的频率分别稳定在和,则口袋中白色球的个数可能是( )
A. B. C. D.
6.已知一组数据有80个,其中最大值为143,最小值为50,取组距为10,则可分成( ).
A.10组 B.9组 C.8组 D.7组
7.(2019八下·淮安月考)某校八年级共有500名学生,为了了解这些学生的视力情况,随机抽査了40名学生的视力,对所得数据进行整理.若数据在4.8~5.0这一小组的频率为0.4,则可估计该校八年级学生视力在4.8~5.0范围内的人数有( )
A.300 B.200 C.150 D.16
8.(2015八下·杭州期中)如图是某学校全体教职工年龄的频数分布直方图(每组年龄包含最小值,不包含最大值),根据图形提供的信息,下列说法中错误的是( )
A.该学校教职工总人数是50人
B.这一组年龄在40≤x<42小组的教职工人数占该学校全体教职工总人数的20%
C.教职工年龄的中位数一定落在40≤x<42这一组
D.教职工年龄的众数一定在38≤x<40这一组
9.有40个数据,共分成6组,第1﹣4组的频数分别是10、5、7、6.第5组占10%,则第6组占( )
A.25% B.30% C.15% D.20%
二、填空题
10.(2019七下·武昌期末)已知10个数据:0,1,2,6,2,1,2,3,0,3,其中 2 出现的频数为 .
11.(2019七下·江汉期末)整理某个样本,其中最大值是24,最小值是2,取组距为3,则该样本可以分为 组.
12.(2024九下·浦东模拟)某校高一年级一班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),则成绩在90.5 95.5这一分数段的频率是
13.八年级(1)班共有50名学生,若有36名学生推荐李明为学习委员,则李明得票的频率是 .
14.在06006000600006的各个数位中,数字“6”出现的频率是
三、计算题
(2023·鹿城模拟)某校有甲、乙两队跳远运动员(每队人数相同),两队开展了为期一个月的跳远强化训练.在强化训练之后,田战宾老师将这两队运动员的跳远成绩(均为正整数)制作成如图所示的统计图及不完整的统计表(十分制,单位:分)
乙队运动员的成绩统计表
成绩/分 6 7 8 9 10
人数/人 1 3 m 5 3
15.求m的值.
16.将下表(单位:分)补充完整;
平均数 众数 中位数
甲队 ________ 8 ________
乙队 8.3 ________ ________
17.经计算,训练后甲队成绩的方差为1.15,乙队成绩的方差为1.11,综合考虑,田战宾老师很有可能选择哪个队代表学校参加市里比赛?并说明理由.
四、解答题
18.(2025·涪城模拟)某校九年级(5)班50名学生参加1分钟跳绳比赛.1分钟跳绳次数与频数经统计后绘制成下面的频数分布表(表示为大于等于60并且小于70)和扇形图.
等级 分数段 1分钟跳绳次数段 频数
A 120 254~300 0
110~120 224~254 3
B 100~110 194~224 9
90~100 164~194 m
C 80~90 148~164 12
70~80 132~148 n
D 60~70 116~132 2
0~60 0~116 0
(1)求m,n的值;
(2)求该班1分钟跳绳成绩在80分以上(含80分)的人数占全班人数的百分比.
19.某部门统计了某地1000名18周岁以上成年男子的身高,得到如下数据:
身高 /cm 频数 身高 /cm 频数
145~150 6 175~180 180
150~155 23 180~185 110
155~160 65 185~190 47
160~165 130 190~195 15
165~170 203 195~200 3
170~175 218
根据上述数据,绘制频数直方图。
20.(2024七下·长沙期末)为了解冬训效果,某足球运动基地对参训队员进行一次体质检测,已知本次检测满分为100分,测试成绩取整数,测试结束后将测试成绩制成尚不完整的频数分布表和频数分布直方图.从测试结果来看,每名队员的成绩均超过50分.
分组 频数 频率
4 0.08
16 0.32
16 0.32
合计
1.00
请解答下列问题:
(1) , , .
(2)补全频数分布直方图.
(3)若成绩在70分以上(不含70分)为冬训效果显著,同时冬训效果显著的人数占总人数的以上,就表示该基地冬训方案科学,请根据上述数据分析该基地冬训方案是否科学,并说明理由.
21.“品中华诗词,寻文化基因”,某校举办了第二届“中华诗词大赛”,将该校七年级参加竞赛的学生成绩统计后,绘制了如下不完整的频数表与如图所示的频数直方图.
参加竞赛的学生成绩频数表
组别 成绩x(分) 人数 百分比
A 60≤x<70 8 20%
B 70≤x<80 16 m%
C 80≤x<90 a 30%
D 90≤x≤100 4 10%
参加竞赛的学生成绩频数直方图
解决下列问题:
(1)表中a= ,m= .
(2)补全频数直方图.
(3)方方参加了这次竞赛,成绩下来后,他对圆圆说:“我这次竞赛的成绩位于中游,比我答得好的人比比我答得差的人少3个.”请你算一算,方方是第几名?
答案解析部分
1.【答案】B
【知识点】频数与频率
2.【答案】D
【知识点】频数(率)分布直方图
3.【答案】D
【知识点】频数(率)分布直方图
4.【答案】A
【知识点】频数与频率;频数(率)分布表
5.【答案】C
【知识点】频数与频率
6.【答案】A
【知识点】频数(率)分布直方图
7.【答案】B
【知识点】频数与频率
8.【答案】D
【知识点】频数(率)分布直方图
9.【答案】D
【知识点】频数与频率
10.【答案】3
【知识点】频数与频率
11.【答案】8
【知识点】频数(率)分布表
12.【答案】0.4
【知识点】频数与频率;频数(率)分布直方图
13.【答案】0.72
【知识点】频数与频率
14.【答案】
【知识点】频数与频率
【答案】15.解:由题意得,甲队的人数为人,
∵甲乙两队人数相同,
∴乙队的人数为20人,
∴
16.解:甲队的平均数为:(6×1+7×2+8×7+9×6+10×4)÷(1+2+7+6+4)=170÷20=8.5(分),
∵甲队的成绩按从小到大排列,第10,11个成绩是8和9,
∴甲队的中位数是(8+9)÷2=8.5,
∵乙队成绩为8分的人数为7,人数最多,
∴乙队的众数是8,
∵乙队的成绩按从小到大排列,第10,11个成绩都是8,
∴乙队的中位数是(8+8)÷2=8,
故填表如下:
平均数 众数 中位数
甲队 8.5 8 8.5
乙队 8.3 8 8
17.解:田战宾老师很有可能会选择甲队作为学校代表参加市里比赛;理由如下:
∵甲、乙两队的方差相差不大,说明两队成绩整齐程度不相上下,但甲队的平均成绩较高,且甲队10分有4人,9分有6人,均比乙队多,
∴田战宾老师很有可能会选择甲队作为学校代表参加市里比赛.
【知识点】频数(率)分布直方图;加权平均数及其计算;中位数;众数
18.【答案】(1),
(2)
【知识点】频数(率)分布表;扇形统计图
19.【答案】解:频数直方图如图所示:
【知识点】频数(率)分布直方图
20.【答案】(1)8,6,0.16;
(2)解:补全频数分布直方图如下图所示:
(3)解:该基地冬训方案科学,理由如下:
由题意知70分以上的人数为:(人),
∵冬训效果显著的人数占总人数的百分比为:,
∴该基地冬训方案科学.
【知识点】频数(率)分布表;频数(率)分布直方图
21.【答案】(1)12;40
(2)解:80≤x<90频数为12,故高度为12,补全频数直方图如下:
(3)解:设比方方答得好的人为x人,则比方方答得差的人数为(x-3)人,
x+(x+3)+1=40,解得x=18;
故方方是第19名;
【知识点】一元二次方程的其他应用;频数(率)分布表;频数(率)分布直方图
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
