1.6.1有理数的乘方(1)(共22张PPT)沪科版数学七年级上册
文档属性
| 名称 | 1.6.1有理数的乘方(1)(共22张PPT)沪科版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 941.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-15 17:20:51 | ||
图片预览







文档简介
(共22张PPT)
第一章 有理数
1.6.1 有理数的乘方
1.理解有理数的乘方以及底数、指数和幂的概念, 会确定一个乘方的底数和指数;
2.掌握有理数乘方的运算法则;熟练进行有理数的 乘方运算。
学习目标
兔兔,我给你的报酬是每天100元,支付一年 .
好的呢,不过我想按我的支付方式,你第一天给我1角钱,第二天给我2角钱,以此类推,后一天是前一天的2倍,我只要你第20天这一天的工资就够了。
100+100·······+100
365个100
=100×365
=36500
第一天 第二天 第三天 第四天······ 第二十天
2
2×2
2×2×2
2×2×2 ······×2=
19个2
1
边长为3的正方形
的面积是______.
3×3可以记作___,
读作_________.
3
3
3×3
32
3的平方
9
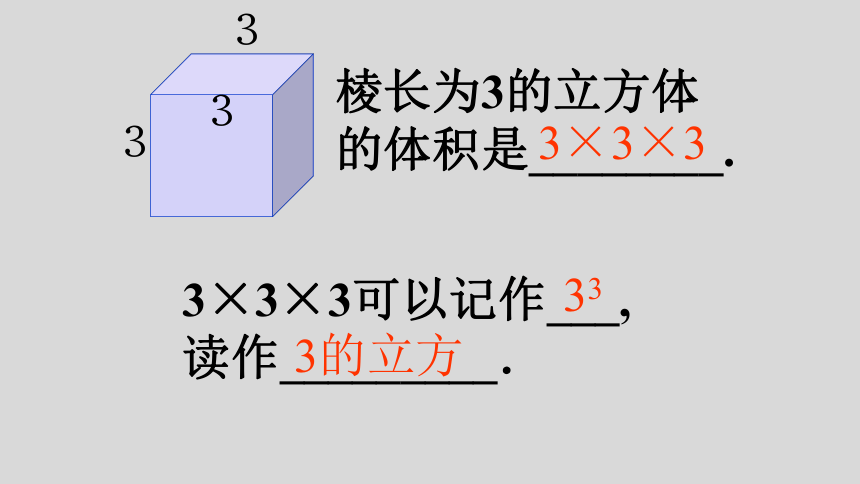
棱长为3的立方体
的体积是________.
3×3×3可以记作___,
读作_________.
3
3
3
3×3×3
33
3的立方
2×2 可以记作_________读作________________;
2×2×2 可以记作________读作________________;
(-3)×(-3)×(-3)×(-3)可以记作_______ ,
读作__________________
可以记作_______ ,
读作________________
2的2次方
2的3次方
-3的4次方
的5次方
可以记作________________ -
读作:a的n次方
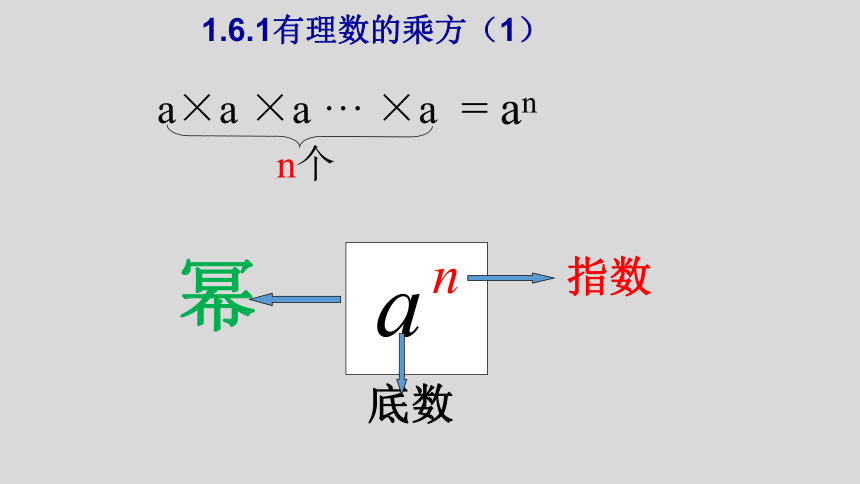
a×a ×a ··· ×a
n个
= an
这种求n个相同因数的积的运算叫做
乘方的结果叫做
乘方
幂
乘方的定义
1.6.1有理数的乘方(1)
幂
指数
底数
a×a ×a ··· ×a
n个
= an
把下列乘积写成乘方的形式,并说出底数和指数
=__________
=______________
底数为_________,指数为______
底数为_________,指数为______
-6
4
5
当底数是负数或分数时,底数一定要加上括号.
读作:______________
读作:______________
=_________________________=________
=__________________________=_________
和
相同吗 ______________
你可以从哪些方面总结出不同?
想一想
-2的4次方
2的4次方相反数
-16
16
不相同
小组讨论 (2分钟)
括号
很重要
想一想
计算并发现其规律。
(1)
(2)
(3)
(4)
-1
1
-8
16
(5)
(6)
0.001
10000
(6)
0
想一想
计算并发现其规律。
(1)
(2)
(3)
(4)
-1
1
-8
16
负数
奇
负数
偶
正数
(5)
(6)
0.001
10000
显然,正数的任何次幂都是_________,
小结:发现(1)(2)(3)(4)的底数为______________
从(1)(3)发现其指数都为_____数,其结果为________;
从(2)(4)发现其指数都为_____数,其结果__________。
0的任何正整数次幂都是_____
正数
0
(6)
0
非0有理数的乘方,将其绝对值乘方,而结果的符号是:
负数的奇次乘方取负号 ,
偶次乘方是正号.
乘方运算的法则:
0的任何次乘方都是0.
正数的任何次乘方都取正号;
牛刀小试 快速说出下列答案的符号
巩固练习(B)
1、计算,比一比:看谁算得又对又快。
1
-1
4
-4
2、如果 a 的倒数是-1,那么 等于( )
A、1 B、2 C、2015 D、-2015
3、下列计算错误的是( )
A. B.
C. D.
A
D
4、下列各数互为相反数的是( )
A.
与
B.
与
C.
与-
D.-
与
C
每天100元,支付一年
36500元
第20天这一天的工资
524288(角)
52428.8元
创设情景,感受乘方
将一张足够大的厚0.1毫米的纸,连续对折30次,猜猜有多高呢?有一本书厚吗?有一层楼高吗?有珠穆朗玛峰高吗?(如果一层楼按3米计算,珠穆朗玛峰高8844.43米)
分析:0.1毫米×230=0.1毫×1073741824
=107374.1824米
107374.1824 ÷3≈36(层)
107374.1824 ÷ 8844.43≈12(座)
an
指数
(因数的个数)
幂
底数
(相同因数)
a×a ×… ×a ×a
n个a
=an
谈体验收获
自主、探究、合作、交流学习方式
分类讨论、化归的数学思想
乘方的定义:
求n个相同因数积的运算叫做乘方.
谢谢观看
第一章 有理数
1.6.1 有理数的乘方
1.理解有理数的乘方以及底数、指数和幂的概念, 会确定一个乘方的底数和指数;
2.掌握有理数乘方的运算法则;熟练进行有理数的 乘方运算。
学习目标
兔兔,我给你的报酬是每天100元,支付一年 .
好的呢,不过我想按我的支付方式,你第一天给我1角钱,第二天给我2角钱,以此类推,后一天是前一天的2倍,我只要你第20天这一天的工资就够了。
100+100·······+100
365个100
=100×365
=36500
第一天 第二天 第三天 第四天······ 第二十天
2
2×2
2×2×2
2×2×2 ······×2=
19个2
1
边长为3的正方形
的面积是______.
3×3可以记作___,
读作_________.
3
3
3×3
32
3的平方
9
棱长为3的立方体
的体积是________.
3×3×3可以记作___,
读作_________.
3
3
3
3×3×3
33
3的立方
2×2 可以记作_________读作________________;
2×2×2 可以记作________读作________________;
(-3)×(-3)×(-3)×(-3)可以记作_______ ,
读作__________________
可以记作_______ ,
读作________________
2的2次方
2的3次方
-3的4次方
的5次方
可以记作________________ -
读作:a的n次方
a×a ×a ··· ×a
n个
= an
这种求n个相同因数的积的运算叫做
乘方的结果叫做
乘方
幂
乘方的定义
1.6.1有理数的乘方(1)
幂
指数
底数
a×a ×a ··· ×a
n个
= an
把下列乘积写成乘方的形式,并说出底数和指数
=__________
=______________
底数为_________,指数为______
底数为_________,指数为______
-6
4
5
当底数是负数或分数时,底数一定要加上括号.
读作:______________
读作:______________
=_________________________=________
=__________________________=_________
和
相同吗 ______________
你可以从哪些方面总结出不同?
想一想
-2的4次方
2的4次方相反数
-16
16
不相同
小组讨论 (2分钟)
括号
很重要
想一想
计算并发现其规律。
(1)
(2)
(3)
(4)
-1
1
-8
16
(5)
(6)
0.001
10000
(6)
0
想一想
计算并发现其规律。
(1)
(2)
(3)
(4)
-1
1
-8
16
负数
奇
负数
偶
正数
(5)
(6)
0.001
10000
显然,正数的任何次幂都是_________,
小结:发现(1)(2)(3)(4)的底数为______________
从(1)(3)发现其指数都为_____数,其结果为________;
从(2)(4)发现其指数都为_____数,其结果__________。
0的任何正整数次幂都是_____
正数
0
(6)
0
非0有理数的乘方,将其绝对值乘方,而结果的符号是:
负数的奇次乘方取负号 ,
偶次乘方是正号.
乘方运算的法则:
0的任何次乘方都是0.
正数的任何次乘方都取正号;
牛刀小试 快速说出下列答案的符号
巩固练习(B)
1、计算,比一比:看谁算得又对又快。
1
-1
4
-4
2、如果 a 的倒数是-1,那么 等于( )
A、1 B、2 C、2015 D、-2015
3、下列计算错误的是( )
A. B.
C. D.
A
D
4、下列各数互为相反数的是( )
A.
与
B.
与
C.
与-
D.-
与
C
每天100元,支付一年
36500元
第20天这一天的工资
524288(角)
52428.8元
创设情景,感受乘方
将一张足够大的厚0.1毫米的纸,连续对折30次,猜猜有多高呢?有一本书厚吗?有一层楼高吗?有珠穆朗玛峰高吗?(如果一层楼按3米计算,珠穆朗玛峰高8844.43米)
分析:0.1毫米×230=0.1毫×1073741824
=107374.1824米
107374.1824 ÷3≈36(层)
107374.1824 ÷ 8844.43≈12(座)
an
指数
(因数的个数)
幂
底数
(相同因数)
a×a ×… ×a ×a
n个a
=an
谈体验收获
自主、探究、合作、交流学习方式
分类讨论、化归的数学思想
乘方的定义:
求n个相同因数积的运算叫做乘方.
谢谢观看
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
