2024-2025学年北师大版九年级上册数学 1.2矩形的判定与性质 题型总结(含答案)
文档属性
| 名称 | 2024-2025学年北师大版九年级上册数学 1.2矩形的判定与性质 题型总结(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-15 18:53:37 | ||
图片预览

文档简介
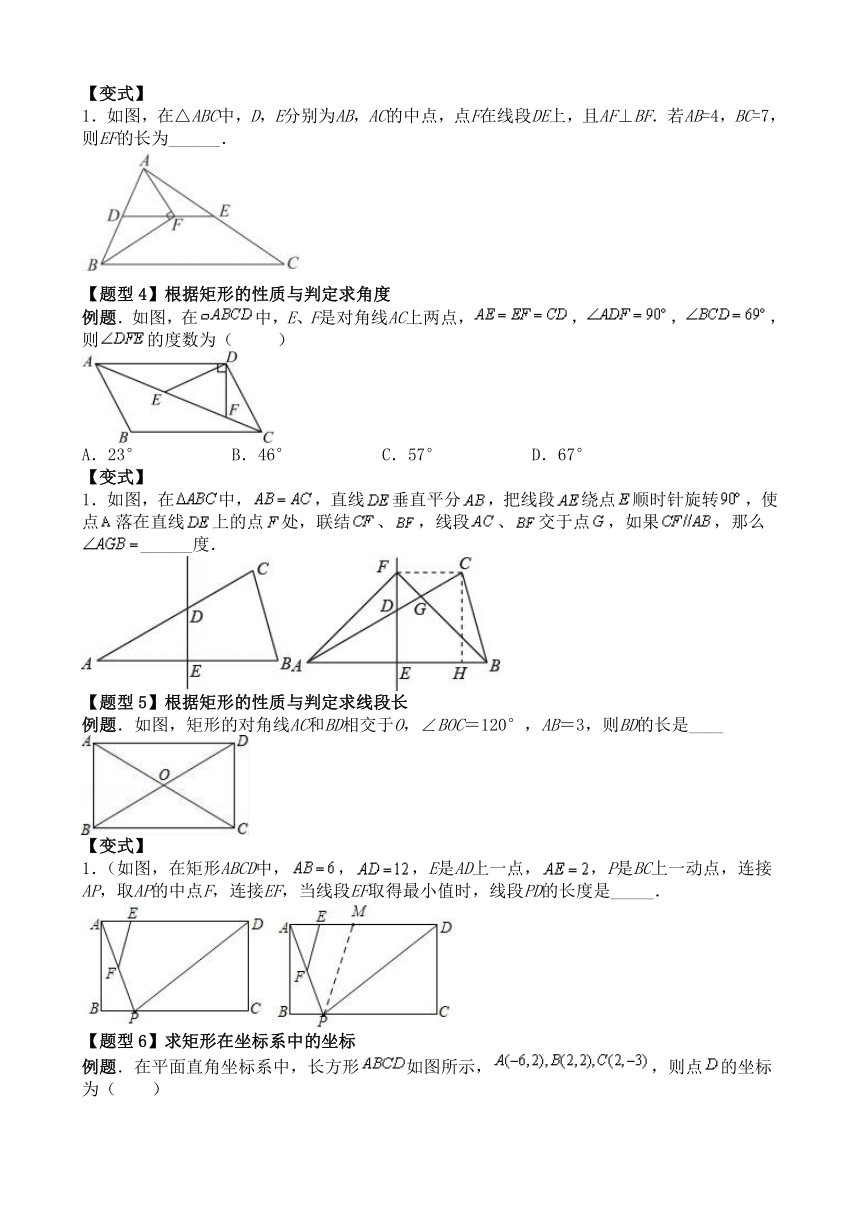
1.2矩形题型总结
【题型1】利用矩形的性质求解
例题.如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为( )
A. B. C. D.
【变式1-1】
1.如图,在矩形中,交于点O,于点E,,则的度数为_______
【变式1-2】
2.如图,在矩形中,对角线,相交于点,点是边的中点,点在对角线上,且,连接.若,则_____.
【题型2】证明四边形是矩形
例题.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
【变式】
1.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加一个条件 _____,能使四边形EFGH是矩形.
【题型3】直角三角形中斜边上的中线
例题.如图,在中,,是斜边上的中线,若,的长为( )
A.6 B.5 C.3 D.1.5
【变式】
1.如图,在△ABC中,D,E分别为AB,AC的中点,点F在线段DE上,且AF⊥BF.若AB=4,BC=7,则EF的长为______.
【题型4】根据矩形的性质与判定求角度
例题.如图,在中,E、F是对角线AC上两点,,,,则的度数为( )
A.23° B.46° C.57° D.67°
【变式】
1.如图,在中,,直线垂直平分,把线段绕点顺时针旋转,使点落在直线上的点处,联结、,线段、交于点,如果,那么______度.
【题型5】根据矩形的性质与判定求线段长
例题.如图,矩形的对角线AC和BD相交于O,∠BOC=120°,AB=3,则BD的长是____
【变式】
1.(如图,在矩形ABCD中,,,E是AD上一点,,P是BC上一动点,连接AP,取AP的中点F,连接EF,当线段EF取得最小值时,线段PD的长度是_____.
【题型6】求矩形在坐标系中的坐标
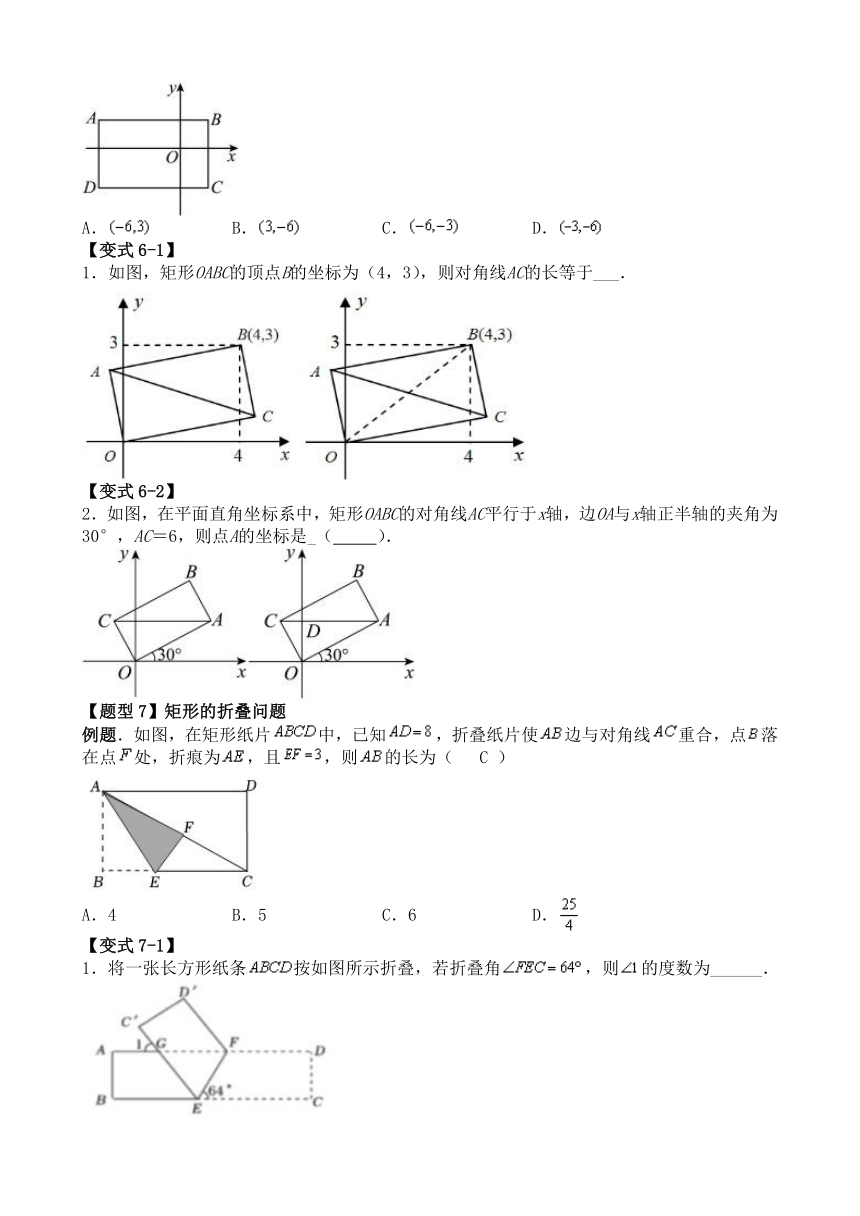
例题.在平面直角坐标系中,长方形如图所示,,则点的坐标为( )
A. B. C. D.
【变式6-1】
1.如图,矩形OABC的顶点B的坐标为(4,3),则对角线AC的长等于___.
【变式6-2】
2.如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,AC=6,则点A的坐标是_( ).
【题型7】矩形的折叠问题
例题.如图,在矩形纸片中,已知,折叠纸片使边与对角线重合,点落在点处,折痕为,且,则的长为( C )
A.4 B.5 C.6 D.
【变式7-1】
1.将一张长方形纸条按如图所示折叠,若折叠角,则的度数为______.
【变式7-2】
2.如图,在长方形中,,将沿翻折,使得点落在边上处,则折痕的长是______.
1.2矩形题型总结答案
【题型1】利用矩形的性质求解
例题.解:∵∠AOD=120°,∴∠AOB=60°,∵四边形ABCD是矩形,∴OA=OC=AC=OB=OD=BD=4(cm),∴△AOB是等边三角形,∴AB=OA=4(cm),
【变式】【详解】解:∵四边形是矩形,∴,
∴,∴,∵,∴,∵,
∴,
【变式1-2】【详解】解:∵在矩形中,,∴,,
∴为的中点,∵点是边的中点,∴;
【题型2】证明四边形是矩形
例题.【详解】证:∵四边形ABCD中,AB=CD,AD=BC,∴四边形ABCD是平行四边形,∴AC=2AO,BD=2OD,∵OA=OD,∴AC=BD,∴四边形ABCD是矩形.
【变式】
1.解:如图,∵G、H、E分别是BC、CD、AD的中点, ∴ ∴∠EHG=∠1,∠1=∠2, ∴∠2=∠EHG, 同理: ∴四边形EFGH是平行四边形,当∠EHG=90°, 四边形EFGH是矩形,∴∠2=90°, ∴AC⊥BD. 故还要添加AC⊥BD,才能保证四边形EFGH是矩形.
【题型3】直角三角形中斜边上的中线
例题.【详解】解:,,又是的中点,
【变式】
1.解:∵点D、E分别是边AB、AC的中点,∴DE是△ABC的中位线,∵BC=7,∴DE=BC=×7=.∵AF⊥BF,D是AB的中点,AB=4,∴DF=AB=×4=2,∴EF=DE-DF=-2=.故答案为:.
【题型4】根据矩形的性质与判定求角度
例题.解:设∠ADE=x, ∵AE=EF,∠ADF=90°, ∴∠DAE=∠ADE=x, ∵AE=EF=CD, ∴DE=CD, ∴∠DCE=∠DEC=2x, ∵四边形ABCD是平行四边形, ∴, ∴∠DAE=∠BCA=x, ∴∠DCE=∠BCD-∠BCA=69°-x, ∴2x=69°-x, 解得:x=23°, 即∠ADE=23°, ∴∠DAE=23°, ∴∠DFE=90°-∠DAE=67°. 故选:D.
【变式】
1.解:过点C作CH⊥AB于H,∵线段AE绕点E顺时针旋转90°,使点A落在直线DE上的点F处,
∴AE=EF,∵直线DE垂直平分AB,AB=AC,∴AE=BE=AB=AC,∠BEF=90°,∴EF=BE=AE,∴△BEF是等腰直角三角形,∴∠EBF=45°,∵DE⊥AB,CF AB,∴CF⊥DE,∵DE⊥AB,CH⊥AB, ∴四边形EFCH是矩形,∴CH=EF=AB=AC,∴∠CAH=30°,∴∠AGB=180° ∠EBF ∠CAH=180° 45° 30°=105°.故答案为:105.
【题型5】根据矩形的性质与判定求线段长
例题.【详解】解:∵∠BOC=120°,∴∠AOB=180°﹣∠BOC=180°﹣120°=60°,∵四边形ABCD是矩形,∴AO=BO=OD,∴△AOB是等边三角形,∴AO=OB=AB=3,∴BD=2OB=6.故答案为6
【变式】
1.【详解】过点 P 作 PM∥FE交AD于M ,如图, F为AP的中点, PM∥FE ,FE为△APM的中位线,
∴AM =2AE=4 ,PM =2EF ,当EF取最小值时,即PM最短,当PM⊥AD时,PM最短,此时PM = AB =6,DM=8 ,在Rt△PMD中,PD =10 ,当线段EF取得最小值时,线段PD的长度是10.故答案为:10·
【题型6】求矩形在坐标系中的坐标
例题.【详解】解:∵四边形为长方形,∴,,∵,
∴点的横坐标与点相同,为,点的纵坐标与点相同,为,∴点的坐标为.
【变式6-1】
1.【详解】如图,连接OB,∵B的坐标为(4,3),∴∵四边形OABC是矩形
∴AC=OB=5故答案为:5.
【变式6-2】
【详解】解:如图所示:∵四边形OABC是矩形,∴∠AOC=90°,∵AC∥x轴,∴∠OAC=30°,∠ODA=90°,∵AC=6,∴OC=AC=3,∴OA=OC=3,∴OD=OA=,∴AD=OD=,∴点A的坐标是(,);故答案为:(,).
【题型7】矩形的折叠问题
例题.【详解】解:∵四边形是矩形,,∴,∵是翻折而成,
∴,是直角三角形,∴,
在中,,设,
在中,,即,解得,
【变式7-1】
1.【详解】解:由翻折可知,,,
是长方形,,,故答案为:.
【变式7-2】
【详解】解:将沿翻折,使得点落在边上处,∴,∴,
∵在长方形中,,∴,∴,
设,根据勾股定理可得,,,
解得,∴,则,故答案为:.
【题型1】利用矩形的性质求解
例题.如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为( )
A. B. C. D.
【变式1-1】
1.如图,在矩形中,交于点O,于点E,,则的度数为_______
【变式1-2】
2.如图,在矩形中,对角线,相交于点,点是边的中点,点在对角线上,且,连接.若,则_____.
【题型2】证明四边形是矩形
例题.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
【变式】
1.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加一个条件 _____,能使四边形EFGH是矩形.
【题型3】直角三角形中斜边上的中线
例题.如图,在中,,是斜边上的中线,若,的长为( )
A.6 B.5 C.3 D.1.5
【变式】
1.如图,在△ABC中,D,E分别为AB,AC的中点,点F在线段DE上,且AF⊥BF.若AB=4,BC=7,则EF的长为______.
【题型4】根据矩形的性质与判定求角度
例题.如图,在中,E、F是对角线AC上两点,,,,则的度数为( )
A.23° B.46° C.57° D.67°
【变式】
1.如图,在中,,直线垂直平分,把线段绕点顺时针旋转,使点落在直线上的点处,联结、,线段、交于点,如果,那么______度.
【题型5】根据矩形的性质与判定求线段长
例题.如图,矩形的对角线AC和BD相交于O,∠BOC=120°,AB=3,则BD的长是____
【变式】
1.(如图,在矩形ABCD中,,,E是AD上一点,,P是BC上一动点,连接AP,取AP的中点F,连接EF,当线段EF取得最小值时,线段PD的长度是_____.
【题型6】求矩形在坐标系中的坐标
例题.在平面直角坐标系中,长方形如图所示,,则点的坐标为( )
A. B. C. D.
【变式6-1】
1.如图,矩形OABC的顶点B的坐标为(4,3),则对角线AC的长等于___.
【变式6-2】
2.如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,AC=6,则点A的坐标是_( ).
【题型7】矩形的折叠问题
例题.如图,在矩形纸片中,已知,折叠纸片使边与对角线重合,点落在点处,折痕为,且,则的长为( C )
A.4 B.5 C.6 D.
【变式7-1】
1.将一张长方形纸条按如图所示折叠,若折叠角,则的度数为______.
【变式7-2】
2.如图,在长方形中,,将沿翻折,使得点落在边上处,则折痕的长是______.
1.2矩形题型总结答案
【题型1】利用矩形的性质求解
例题.解:∵∠AOD=120°,∴∠AOB=60°,∵四边形ABCD是矩形,∴OA=OC=AC=OB=OD=BD=4(cm),∴△AOB是等边三角形,∴AB=OA=4(cm),
【变式】【详解】解:∵四边形是矩形,∴,
∴,∴,∵,∴,∵,
∴,
【变式1-2】【详解】解:∵在矩形中,,∴,,
∴为的中点,∵点是边的中点,∴;
【题型2】证明四边形是矩形
例题.【详解】证:∵四边形ABCD中,AB=CD,AD=BC,∴四边形ABCD是平行四边形,∴AC=2AO,BD=2OD,∵OA=OD,∴AC=BD,∴四边形ABCD是矩形.
【变式】
1.解:如图,∵G、H、E分别是BC、CD、AD的中点, ∴ ∴∠EHG=∠1,∠1=∠2, ∴∠2=∠EHG, 同理: ∴四边形EFGH是平行四边形,当∠EHG=90°, 四边形EFGH是矩形,∴∠2=90°, ∴AC⊥BD. 故还要添加AC⊥BD,才能保证四边形EFGH是矩形.
【题型3】直角三角形中斜边上的中线
例题.【详解】解:,,又是的中点,
【变式】
1.解:∵点D、E分别是边AB、AC的中点,∴DE是△ABC的中位线,∵BC=7,∴DE=BC=×7=.∵AF⊥BF,D是AB的中点,AB=4,∴DF=AB=×4=2,∴EF=DE-DF=-2=.故答案为:.
【题型4】根据矩形的性质与判定求角度
例题.解:设∠ADE=x, ∵AE=EF,∠ADF=90°, ∴∠DAE=∠ADE=x, ∵AE=EF=CD, ∴DE=CD, ∴∠DCE=∠DEC=2x, ∵四边形ABCD是平行四边形, ∴, ∴∠DAE=∠BCA=x, ∴∠DCE=∠BCD-∠BCA=69°-x, ∴2x=69°-x, 解得:x=23°, 即∠ADE=23°, ∴∠DAE=23°, ∴∠DFE=90°-∠DAE=67°. 故选:D.
【变式】
1.解:过点C作CH⊥AB于H,∵线段AE绕点E顺时针旋转90°,使点A落在直线DE上的点F处,
∴AE=EF,∵直线DE垂直平分AB,AB=AC,∴AE=BE=AB=AC,∠BEF=90°,∴EF=BE=AE,∴△BEF是等腰直角三角形,∴∠EBF=45°,∵DE⊥AB,CF AB,∴CF⊥DE,∵DE⊥AB,CH⊥AB, ∴四边形EFCH是矩形,∴CH=EF=AB=AC,∴∠CAH=30°,∴∠AGB=180° ∠EBF ∠CAH=180° 45° 30°=105°.故答案为:105.
【题型5】根据矩形的性质与判定求线段长
例题.【详解】解:∵∠BOC=120°,∴∠AOB=180°﹣∠BOC=180°﹣120°=60°,∵四边形ABCD是矩形,∴AO=BO=OD,∴△AOB是等边三角形,∴AO=OB=AB=3,∴BD=2OB=6.故答案为6
【变式】
1.【详解】过点 P 作 PM∥FE交AD于M ,如图, F为AP的中点, PM∥FE ,FE为△APM的中位线,
∴AM =2AE=4 ,PM =2EF ,当EF取最小值时,即PM最短,当PM⊥AD时,PM最短,此时PM = AB =6,DM=8 ,在Rt△PMD中,PD =10 ,当线段EF取得最小值时,线段PD的长度是10.故答案为:10·
【题型6】求矩形在坐标系中的坐标
例题.【详解】解:∵四边形为长方形,∴,,∵,
∴点的横坐标与点相同,为,点的纵坐标与点相同,为,∴点的坐标为.
【变式6-1】
1.【详解】如图,连接OB,∵B的坐标为(4,3),∴∵四边形OABC是矩形
∴AC=OB=5故答案为:5.
【变式6-2】
【详解】解:如图所示:∵四边形OABC是矩形,∴∠AOC=90°,∵AC∥x轴,∴∠OAC=30°,∠ODA=90°,∵AC=6,∴OC=AC=3,∴OA=OC=3,∴OD=OA=,∴AD=OD=,∴点A的坐标是(,);故答案为:(,).
【题型7】矩形的折叠问题
例题.【详解】解:∵四边形是矩形,,∴,∵是翻折而成,
∴,是直角三角形,∴,
在中,,设,
在中,,即,解得,
【变式7-1】
1.【详解】解:由翻折可知,,,
是长方形,,,故答案为:.
【变式7-2】
【详解】解:将沿翻折,使得点落在边上处,∴,∴,
∵在长方形中,,∴,∴,
设,根据勾股定理可得,,,
解得,∴,则,故答案为:.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
