华师大版(2024)数学八年级上册课件 11.1.4 同底数幂的除法(15张PPT)
文档属性
| 名称 | 华师大版(2024)数学八年级上册课件 11.1.4 同底数幂的除法(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
11.1.4 同底数幂的除法
1.理解同底数幂的除法法则.(重点)
2.会用同底数幂的除法法则进行计算.(难点)
1.同底数幂的乘法法则是什么?
同底数幂相乘, .
2.计算:
23×24= ;a2·a3= .
底数不变,指数相加
am·an=am+n(m,n是正整数)
3.根据乘除互为逆运算,请大胆猜想:
27÷23= ;a5÷a3= .
27
a5
24
a2
1.计算:
(1)25×23=? (2)x6·x4=
(3)2m×2n= ?
28
x10
2m+n
2.填空:
(1)( )( ) ×23=28 (2)x6·( )( )=x10
(3)( )( )×2n=2m+n
2
5
x
4
2
m
相当于求28÷23=?
相当于求x10÷x6=?
相当于求2m+n÷2n=?
观察上面各题等式,底数、指数有什么规律?
试猜想:am÷an= (m,n都是正整数,且mn)
(1)28÷23=25
(2)x10÷x6=x4
(3)2m+n÷2n=2m
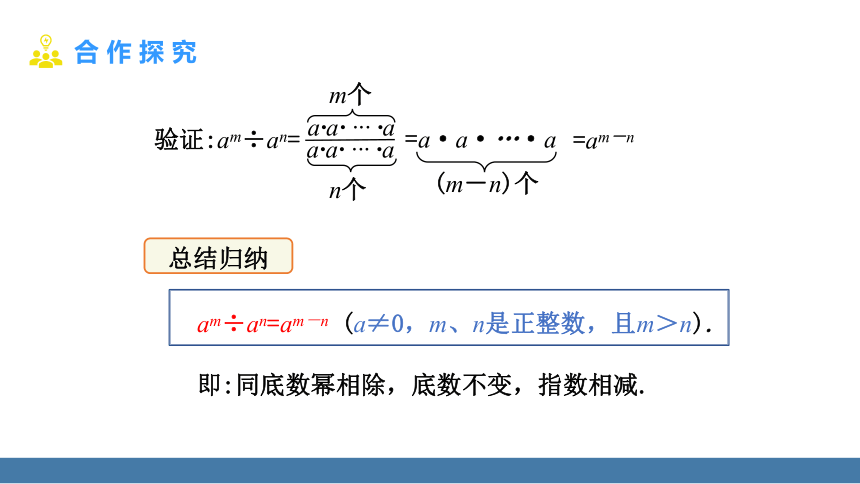
验证:am÷an=
m个
n个
=a·a·…·a
(m-n)个
=am-n
总结归纳
(a≠0,m、n是正整数,且m>n).
am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
a·a· ··· ·a
a·a· ··· ·a
例1 计算:
(1) a8÷a3; (2)(-a )10 ÷(-a )3; (3)(2a )7÷(2a )4 .
解:(1) a8÷a3=a8-3=a5.
(2)(-a )10 ÷(-a )3=(-a )10-3=(-a )7=-a7.
(3)(2a )7÷(2a )4 =(2a )7-4=(2a )3=8a3.
总结:①幂的指数、底数都应是最简的;
②底数中系数不能为负;
③幂的底数是积的形式时,要再用一次(ab)n=anbn.
注意:最后结果
中幂的形式应是
最简的.
(a+b)4÷(a+b)2= 能否用同底数幂的除法法则进行计算?
同底数幂的除法,底数可以是数、单项式,也可以是多项式.
(a±b)m÷(a±b)n=(a±b)m-n
(a+b)4÷(a+b)2=(a+b)2.
例2 计算:
(1)(x-1)3÷(x-1)2;(2)(3a)6÷(3a)4.
解:(1)(x-1)3÷(x-1)2=(x-1)3-2=x-1;
(2)(3a)6÷(3a)4=(3a)6-4=(3a)2=9a2.
例3 已知:am=3,an=5.求:(1)am-n的值;(2)a3m-3n的值.
解:(1) am-n= am ÷ an
(2) a3m-3n= a 3m ÷ a 3n
同底数幂的除法可以逆用:am-n=am÷an
= 3 ÷5
= 0.6;
= (am)3 ÷(an)3
=33 ÷53
=27 ÷125
= .
1.下列运算正确的是( )
A.a+2a=3a2 B.3a3·2a2=6a6
C.a8÷a2=a4 D.(2a)3=8a3
2.计算106×(102)3÷104的结果是( )
A.103 B.107 C.108 D.109
D
C
3.计算:
(1)a10÷(-a2)3;
(2)(y3)3÷y3÷(-y2)2;
(3)[(xn+1)4·x2]÷[(xn+2)3÷(x2)n];
解:原式=a10÷(-a6)=-a4.
解:原式=x4n+4+2÷(x3n+6÷x2n)
=x4n+6÷xn+6
=x3n.
解:原式=y9÷y3÷y4=y2.
解:原式=a2m+4-a2m+6÷a2=a2m+4-a2m+4=0.
(4)(a·am+1)2-(a2)m+3÷a2;
(5)(x-2y)8(2y-x)3÷(x-2y)4(结果用(x-2y)的幂表示).
解:原式=(x-2y)8·[-(x-2y)3]÷(x-2y)4
=-(x-2y)11÷(x-2y)4
=-(x-2y)7.
4.(1)若9m·27m-1÷33m=27,求m的值;
解:∵9m·27m-1÷33m=(32)m·(33)m-1÷33m =32m·33m-3÷33m=35m-3÷33m=32m-3=33,
∴2m-3=3.∴m=3.
(2)若10m=20,10n=,求9m÷32n.
解:9m÷32n=9m÷9n=9m-n.
∵10m÷10n=20÷=100,∴10m-n=102.∴m-n=2.
∴原式=92=81.
法则
同底数幂的除法
am÷an=am-n
(a≠0, m,n都是正整数,且m>n)
同底数幂相除,底数不变,指数相减
同底数幂除法法则的逆用:
am-n=am÷an (a≠0, m,n都是正整数,且m>n)
11.1.4 同底数幂的除法
1.理解同底数幂的除法法则.(重点)
2.会用同底数幂的除法法则进行计算.(难点)
1.同底数幂的乘法法则是什么?
同底数幂相乘, .
2.计算:
23×24= ;a2·a3= .
底数不变,指数相加
am·an=am+n(m,n是正整数)
3.根据乘除互为逆运算,请大胆猜想:
27÷23= ;a5÷a3= .
27
a5
24
a2
1.计算:
(1)25×23=? (2)x6·x4=
(3)2m×2n= ?
28
x10
2m+n
2.填空:
(1)( )( ) ×23=28 (2)x6·( )( )=x10
(3)( )( )×2n=2m+n
2
5
x
4
2
m
相当于求28÷23=?
相当于求x10÷x6=?
相当于求2m+n÷2n=?
观察上面各题等式,底数、指数有什么规律?
试猜想:am÷an= (m,n都是正整数,且mn)
(1)28÷23=25
(2)x10÷x6=x4
(3)2m+n÷2n=2m
验证:am÷an=
m个
n个
=a·a·…·a
(m-n)个
=am-n
总结归纳
(a≠0,m、n是正整数,且m>n).
am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
a·a· ··· ·a
a·a· ··· ·a
例1 计算:
(1) a8÷a3; (2)(-a )10 ÷(-a )3; (3)(2a )7÷(2a )4 .
解:(1) a8÷a3=a8-3=a5.
(2)(-a )10 ÷(-a )3=(-a )10-3=(-a )7=-a7.
(3)(2a )7÷(2a )4 =(2a )7-4=(2a )3=8a3.
总结:①幂的指数、底数都应是最简的;
②底数中系数不能为负;
③幂的底数是积的形式时,要再用一次(ab)n=anbn.
注意:最后结果
中幂的形式应是
最简的.
(a+b)4÷(a+b)2= 能否用同底数幂的除法法则进行计算?
同底数幂的除法,底数可以是数、单项式,也可以是多项式.
(a±b)m÷(a±b)n=(a±b)m-n
(a+b)4÷(a+b)2=(a+b)2.
例2 计算:
(1)(x-1)3÷(x-1)2;(2)(3a)6÷(3a)4.
解:(1)(x-1)3÷(x-1)2=(x-1)3-2=x-1;
(2)(3a)6÷(3a)4=(3a)6-4=(3a)2=9a2.
例3 已知:am=3,an=5.求:(1)am-n的值;(2)a3m-3n的值.
解:(1) am-n= am ÷ an
(2) a3m-3n= a 3m ÷ a 3n
同底数幂的除法可以逆用:am-n=am÷an
= 3 ÷5
= 0.6;
= (am)3 ÷(an)3
=33 ÷53
=27 ÷125
= .
1.下列运算正确的是( )
A.a+2a=3a2 B.3a3·2a2=6a6
C.a8÷a2=a4 D.(2a)3=8a3
2.计算106×(102)3÷104的结果是( )
A.103 B.107 C.108 D.109
D
C
3.计算:
(1)a10÷(-a2)3;
(2)(y3)3÷y3÷(-y2)2;
(3)[(xn+1)4·x2]÷[(xn+2)3÷(x2)n];
解:原式=a10÷(-a6)=-a4.
解:原式=x4n+4+2÷(x3n+6÷x2n)
=x4n+6÷xn+6
=x3n.
解:原式=y9÷y3÷y4=y2.
解:原式=a2m+4-a2m+6÷a2=a2m+4-a2m+4=0.
(4)(a·am+1)2-(a2)m+3÷a2;
(5)(x-2y)8(2y-x)3÷(x-2y)4(结果用(x-2y)的幂表示).
解:原式=(x-2y)8·[-(x-2y)3]÷(x-2y)4
=-(x-2y)11÷(x-2y)4
=-(x-2y)7.
4.(1)若9m·27m-1÷33m=27,求m的值;
解:∵9m·27m-1÷33m=(32)m·(33)m-1÷33m =32m·33m-3÷33m=35m-3÷33m=32m-3=33,
∴2m-3=3.∴m=3.
(2)若10m=20,10n=,求9m÷32n.
解:9m÷32n=9m÷9n=9m-n.
∵10m÷10n=20÷=100,∴10m-n=102.∴m-n=2.
∴原式=92=81.
法则
同底数幂的除法
am÷an=am-n
(a≠0, m,n都是正整数,且m>n)
同底数幂相除,底数不变,指数相减
同底数幂除法法则的逆用:
am-n=am÷an (a≠0, m,n都是正整数,且m>n)
