3.1圆的对称性(3)学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 3.1圆的对称性(3)学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 316.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 00:00:00 | ||
图片预览

文档简介
3.1 圆的对称性(3)
【学习目标】
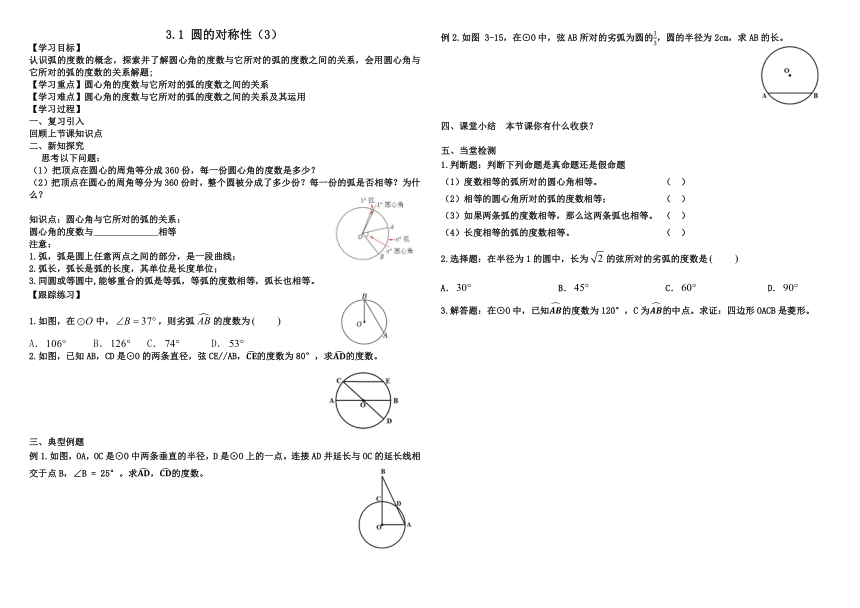
认识弧的度数的概念,探索并了解圆心角的度数与它所对的弧的度数之间的关系,会用圆心角与它所对的弧的度数的关系解题;
【学习重点】圆心角的度数与它所对的弧的度数之间的关系
【学习难点】圆心角的度数与它所对的弧的度数之间的关系及其运用
【学习过程】
复习引入
回顾上节课知识点
二、新知探究
思考以下问题:
(1)把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少?
(2)把顶点在圆心的周角等分为360份时,整个圆被分成了多少份?每一份的弧是否相等?为什么?
知识点:圆心角与它所对的弧的关系:
圆心角的度数与 相等
注意:
1.弧,弧是圆上任意两点之间的部分,是一段曲线;
2.弧长,弧长是弧的长度,其单位是长度单位;
3.同圆或等圆中,能够重合的弧是等弧,等弧的度数相等,弧长也相等。
【跟踪练习】
1.如图,在中,,则劣弧的度数为
A. B. C. D.
2.如图,已知AB,CD是⊙O的两条直径,弦CE//AB,的度数为80°,求的度数。
三、典型例题
例1.如图,OA,OC是⊙O中两条垂直的半径,D是⊙O上的一点。连接AD并延长与OC的延长线相交于点B,∠B = 25°。求,的度数。
例2.如图 3-15,在⊙O中,弦AB所对的劣弧为圆的,圆的半径为2cm,求AB的长。
四、课堂小结 本节课你有什么收获?
五、当堂检测
1.判断题:判断下列命题是真命题还是假命题
(1)度数相等的弧所对的圆心角相等。 ( )
(2)相等的圆心角所对的弧的度数相等; ( )
(3)如果两条弧的度数相等,那么这两条弧也相等。 ( )
(4)长度相等的弧的度数相等。 ( )
2.选择题:在半径为1的圆中,长为的弦所对的劣弧的度数是
A. B. C. D.
3.解答题:在⊙O中,已知的度数为120°,C为的中点。求证:四边形OACB是菱形。
六、课后分层作业
【基础闯关】
1.如图,和是的两条直径,弦,弧为的弧,那么为
A. B.
C. D.
2.如图,在半径为5的中,若弦,则的面积为
A.24 B.16
C.12 D.8
3.若弦长等于半径,则弦所对弧的度数是 .
4.如图,在中,,,以点为圆心,为半径的圆交于点,交于点,求的度数.
5.如图,在中,已知,且,求的度数.
6.如图,已知是的直径,弦.
(1)求证:.
(2)若的度数为,求的度数.
【能力提升】
7.弦把分成两条弧,它们的度数比为,为的中点, 则的度数为
A . B . C . D .
8.如图,是的直径,、为半圆的三等分点,于点,的度数为
A. B. C. D.
9.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是
A. B. C. D.
第8题 第9题
10.如图所示,已知的半径是1,,是直径同侧圆周上的两点,弧的度数为,弧的度数为,动点在直径上,则的最小值为
A.2 B.
C. D.1
11.如图,已知点是的直径上的一点,过点作弦,使.若的度数为,则的度数是 .
【培优创新】
如图,为的直径,弦与的延长线交于点,且,若,求弧的度数.
【学习目标】
认识弧的度数的概念,探索并了解圆心角的度数与它所对的弧的度数之间的关系,会用圆心角与它所对的弧的度数的关系解题;
【学习重点】圆心角的度数与它所对的弧的度数之间的关系
【学习难点】圆心角的度数与它所对的弧的度数之间的关系及其运用
【学习过程】
复习引入
回顾上节课知识点
二、新知探究
思考以下问题:
(1)把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少?
(2)把顶点在圆心的周角等分为360份时,整个圆被分成了多少份?每一份的弧是否相等?为什么?
知识点:圆心角与它所对的弧的关系:
圆心角的度数与 相等
注意:
1.弧,弧是圆上任意两点之间的部分,是一段曲线;
2.弧长,弧长是弧的长度,其单位是长度单位;
3.同圆或等圆中,能够重合的弧是等弧,等弧的度数相等,弧长也相等。
【跟踪练习】
1.如图,在中,,则劣弧的度数为
A. B. C. D.
2.如图,已知AB,CD是⊙O的两条直径,弦CE//AB,的度数为80°,求的度数。
三、典型例题
例1.如图,OA,OC是⊙O中两条垂直的半径,D是⊙O上的一点。连接AD并延长与OC的延长线相交于点B,∠B = 25°。求,的度数。
例2.如图 3-15,在⊙O中,弦AB所对的劣弧为圆的,圆的半径为2cm,求AB的长。
四、课堂小结 本节课你有什么收获?
五、当堂检测
1.判断题:判断下列命题是真命题还是假命题
(1)度数相等的弧所对的圆心角相等。 ( )
(2)相等的圆心角所对的弧的度数相等; ( )
(3)如果两条弧的度数相等,那么这两条弧也相等。 ( )
(4)长度相等的弧的度数相等。 ( )
2.选择题:在半径为1的圆中,长为的弦所对的劣弧的度数是
A. B. C. D.
3.解答题:在⊙O中,已知的度数为120°,C为的中点。求证:四边形OACB是菱形。
六、课后分层作业
【基础闯关】
1.如图,和是的两条直径,弦,弧为的弧,那么为
A. B.
C. D.
2.如图,在半径为5的中,若弦,则的面积为
A.24 B.16
C.12 D.8
3.若弦长等于半径,则弦所对弧的度数是 .
4.如图,在中,,,以点为圆心,为半径的圆交于点,交于点,求的度数.
5.如图,在中,已知,且,求的度数.
6.如图,已知是的直径,弦.
(1)求证:.
(2)若的度数为,求的度数.
【能力提升】
7.弦把分成两条弧,它们的度数比为,为的中点, 则的度数为
A . B . C . D .
8.如图,是的直径,、为半圆的三等分点,于点,的度数为
A. B. C. D.
9.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是
A. B. C. D.
第8题 第9题
10.如图所示,已知的半径是1,,是直径同侧圆周上的两点,弧的度数为,弧的度数为,动点在直径上,则的最小值为
A.2 B.
C. D.1
11.如图,已知点是的直径上的一点,过点作弦,使.若的度数为,则的度数是 .
【培优创新】
如图,为的直径,弦与的延长线交于点,且,若,求弧的度数.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
