1.3几何证明举例(第1课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册
文档属性
| 名称 | 1.3几何证明举例(第1课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 07:54:37 | ||
图片预览


文档简介
(共20张PPT)
青岛版2024·八年级上册
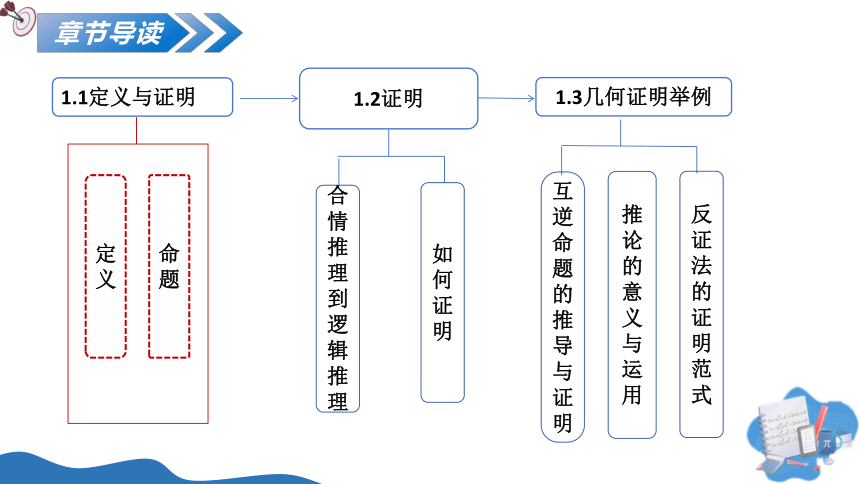
1.3 几何证明举例
第一章
推理与证明
第1课时
互逆命题的推导与证明
章节导读
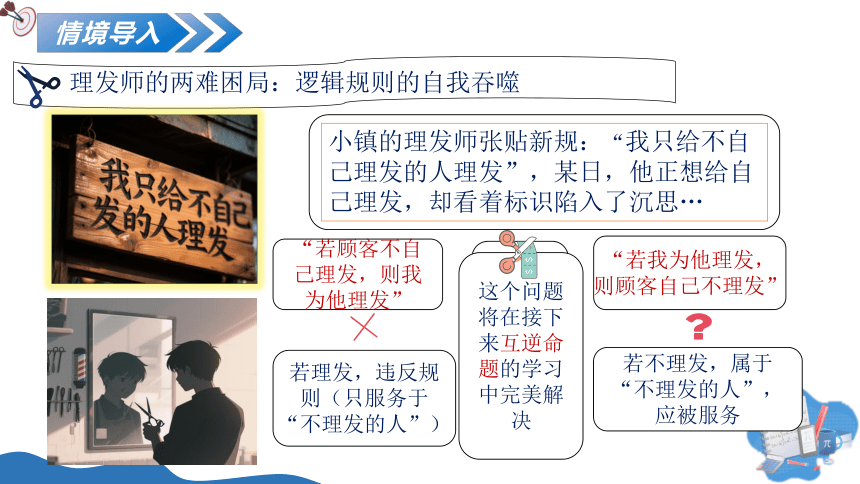
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
如何证明
互逆命题的推导与证明
推论的意义与运用
反证法的证明范式
合情推理到逻辑推理
学 习 目 标
1
2
能够准确识别原命题与逆命题的条件、结论的互换特征,并能够规范书写给定命题的逆命题
掌握运用基本事实与定理进行演绎推理,证明互逆命题真假的方法
3
理解“原命题为真,逆命题未必成立”的核心逻辑,并会举反例判断逆命题的真假性
“若顾客不自己理发,则我为他理发”
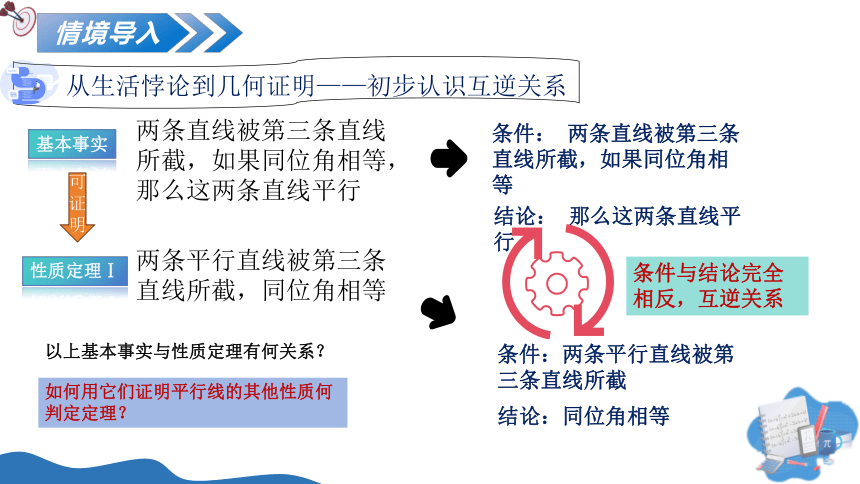
情境导入
理发师的两难困局:逻辑规则的自我吞噬
小镇的理发师张贴新规:“我只给不自己理发的人理发”,某日,他正想给自己理发,却看着标识陷入了沉思…
“若我为他理发,则顾客自己不理发”
若理发,违反规则(只服务于“不理发的人”)
若不理发,属于“不理发的人”,应被服务
这个死循环的根源究竟是什么?
这个问题将在接下来互逆命题的学习中完美解决
情境导入
从生活悖论到几何证明——初步认识互逆关系
基本事实
性质定理Ⅰ
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
两条平行直线被第三条直线所截,同位角相等
条件: 两条直线被第三条直线所截,如果同位角相等
结论: 那么这两条直线平行
条件:两条平行直线被第三条直线所截
结论:同位角相等
条件与结论完全相反,互逆关系
可证明
以上基本事实与性质定理有何关系?
如何用它们证明平行线的其他性质何判定定理?
新知探究
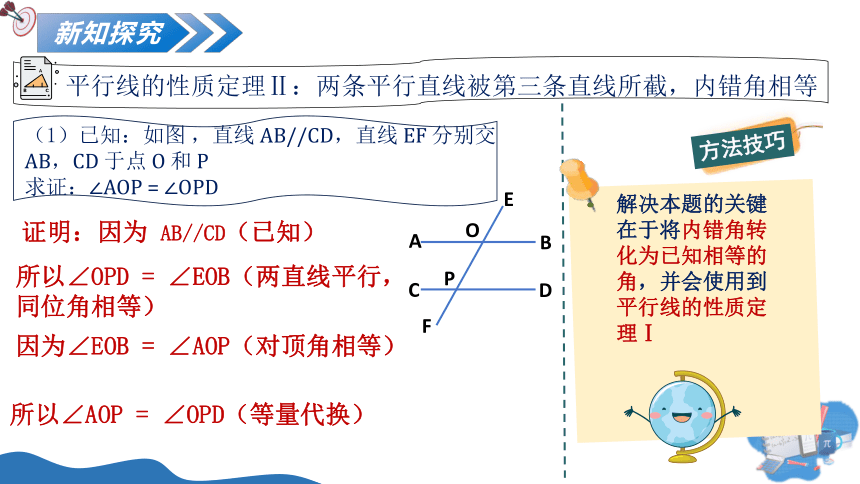
平行线的性质定理Ⅱ:两条平行直线被第三条直线所截,内错角相等
(1)已知:如图 ,直线 AB//CD,直线 EF 分别交 AB,CD 于点 O 和 P
求证:∠AOP = ∠OPD
证明:因为 AB//CD(已知)
所以∠OPD = ∠EOB(两直线平行,同位角相等)
因为∠EOB = ∠AOP(对顶角相等)
所以∠AOP = ∠OPD(等量代换)
A
B
C
D
P
O
方法技巧
解决本题的关键在于将内错角转化为已知相等的角,并会使用到平行线的性质定理Ⅰ
E
F
新知探究
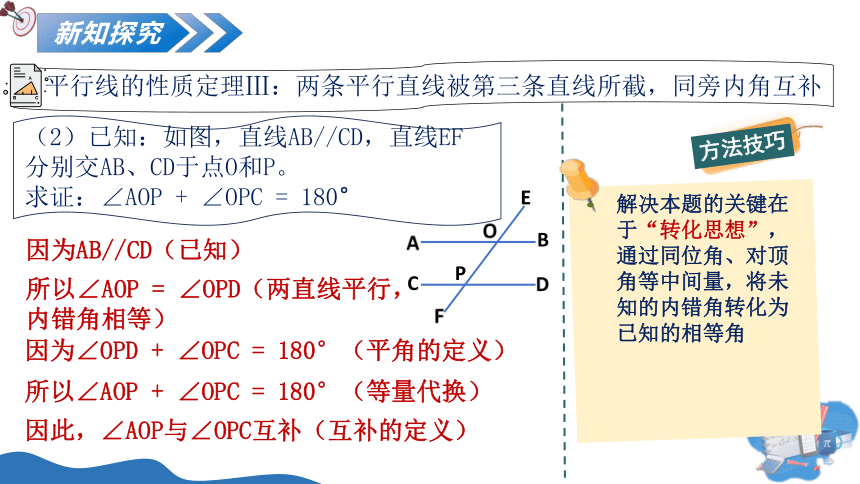
平行线的性质定理Ⅲ:两条平行直线被第三条直线所截,同旁内角互补
(2)已知:如图,直线AB//CD,直线EF分别交AB、CD于点O和P。
求证:∠AOP + ∠OPC = 180°
因为AB//CD(已知)
所以∠AOP = ∠OPD(两直线平行,内错角相等)
因为∠OPD + ∠OPC = 180°(平角的定义)
所以∠AOP + ∠OPC = 180°(等量代换)
因此,∠AOP与∠OPC互补(互补的定义)
B
C
P
方法技巧
解决本题的关键在于“转化思想”,通过同位角、对顶角等中间量,将未知的内错角转化为已知的相等角
新知探究
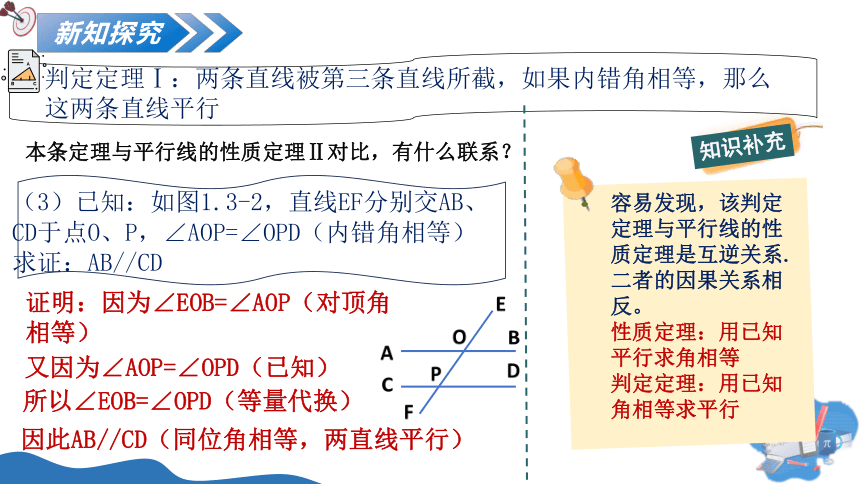
判定定理Ⅰ:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
(3)已知:如图1.3-2,直线EF分别交AB、CD于点O、P,∠AOP=∠OPD(内错角相等)
求证:AB//CD
证明:因为∠EOB=∠AOP(对顶角相等)
又因为∠AOP=∠OPD(已知)
所以∠EOB=∠OPD(等量代换)
因此AB//CD(同位角相等,两直线平行)
知识补充
容易发现,该判定定理与平行线的性质定理是互逆关系.二者的因果关系相反。
性质定理:用已知平行求角相等
判定定理:用已知角相等求平行
本条定理与平行线的性质定理Ⅱ对比,有什么联系?
新知探究
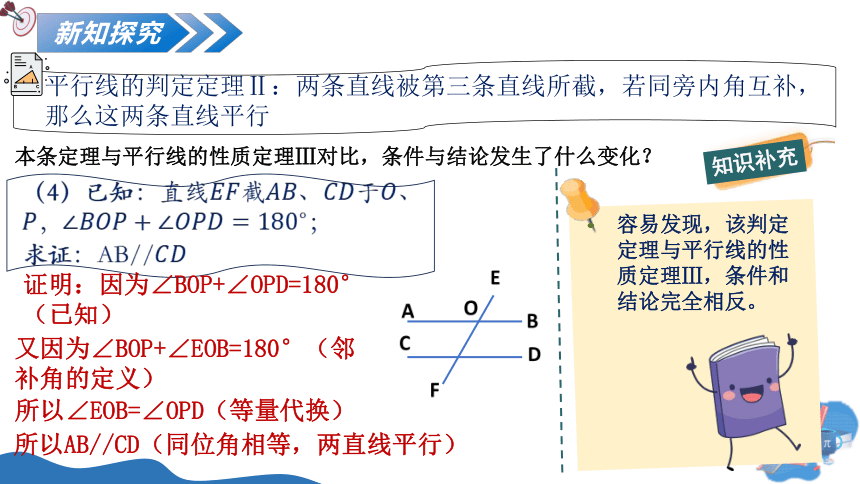
平行线的判定定理Ⅱ:两条直线被第三条直线所截,若同旁内角互补,那么这两条直线平行
本条定理与平行线的性质定理Ⅲ对比,条件与结论发生了什么变化?
(4)已知:直线截、于、,;
求证:AB//
证明:因为∠BOP+∠OPD=180°(已知)
又因为∠BOP+∠EOB=180°(邻补角的定义)
所以∠EOB=∠OPD(等量代换)
所以AB//CD(同位角相等,两直线平行)
知识补充
容易发现,该判定定理与平行线的性质定理Ⅲ,条件和结论完全相反。
知识小结
互逆命题与逆定理——从观察到定义的逻辑之旅
观察上面的(1)和(3),(2)和(4)中的两个命题,它们的条件和结论之间有什么关系?
第一个命题和第二个命题的结论和条件完全相反
概括与表达
互逆命题:
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题叫做互逆命题
逆命题:
如果把其中一个叫做原命题,那么另一个叫做逆命题
逆定理:
如果一个命题的逆命题也是真命题,那么这个逆命题叫做逆定理
原命题成立,逆命题一定成立吗?
即时小练
类型一:互逆命题的判断
1:下列各组命题中,互为逆命题的是( )
A. ① 如果a>0,那么a >0;② 如果a >0,那么a<0
B. ① 两直线平行,同位角相等;② 同位角相等,两直线平行
C. ① 如果x=3,那么x =9;② 如果x ≠9,那么x≠3
D. ① 对顶角相等;② 相等的角是对顶角
条件
结论
条件
结论
并非互逆关系
条件
互逆关系
条件:如果两个角是对顶角
结论:那么它们相等
结论:那么它们是对顶角
条件:如果两个角相等
并非互逆关系
方法技巧
互逆命题的唯一判断依据:两个命题的“条件”和“结论”是否互换(不涉及真假)
原命题:若(条件),则(结论)
逆命题:若(原命题的结论),则(原命题的条件)
即时小练
类型二:逆命题的改写与真假判断
2.写出下列命题的逆命题,并判断这些逆命题是真命题还是假命题。
(1)对顶角相等;
(2)在同一平面内,如果两条直线没有公共点,那么这两条直线平行。
方法技巧
改写逆命题的步骤:
①找出原命题的条件和结论
②将条件与结论互换位置
③调整语句表诉,使其通顺
解:(1)逆命题:如果两个角相等,那么这两个角是对顶角;
真假判断:假命题
(2)逆命题:在同一平面内,如果两条直线平行,那么这两条直线没有公共点;
真假判断:真命题
即时小练
类型三:逆命题的证明
3.已知∠1=∠2求证:∠3+∠4=180°
变式:已知∠3+∠4=180° 求证: ∠1=∠2
结论
条件
证明:因为∠1=∠2(已知)
与变式互为逆命题
与原题互为逆命题
证明:因为∠3+∠4=180°(已知)
所以AB//CD(同位角相等,两直线平行)
所以AB//CD(同旁内角互补,两直线平行)
所以∠3+∠4=180°(两直线平行,同旁内角互补)
所以∠1=∠2(两直线平行,同位角相等)
1
2
3
4
知识小结
原命题与逆命题的逻辑关系——原命题成立,逆命题不一定成立
理发师错误的认为原命题成立,逆命题就一定成立,因此陷入了逻辑困境
类型一与类型二中的题目
原命题成立,逆命题不一定成立
类型三的题目与变式
原命题与逆命题的真假性需要独立证明
回顾情境,你能理解理发师的逻辑困境了吗?
概括与表达
逆命题的正确性需独立判断,不能默认与原命题一致
课堂练习
1.命题“如果两个角是直角,那么它们相等”的逆命题是( )
A.如果两个角相等,那么它们是直角
B. 如果两个角不是直角,那么它们不相等
C. 如果两个角不相等,那么它们不是直角
D. 两个相等的角是直角
基础巩固
条件
结论
逆命题:如果(结论),那么(条件)
综上,答案选A
方法技巧
找逆命题的核心操作就是:
严格交换“条件(p)”和“结论(q)”,且条件和结论在交换后不能发生实际意义上的变化
课堂练习
基础巩固
2.写出下列命题的逆命题,并判断这些逆命题的真假
(1)如果两个角相等,那么这两个角的补角相等;
(2)两条直线被第三条直线所截,如果同位角相等,那么内错角相等。
解:(1)逆命题:如果两个角的补角相等,那么这两个角相等;
真假判断:真命题
(2)逆命题:两条直线被第三条直线所截,如果内错角相等,那么同位角相等;
真假判断:真命题
方法技巧
逆命题的真假需要独立判断,本题两个逆命题都为真,但并非所有逆命题都为真
课堂练习
基础巩固
3. 阅读证明过程,并在括号内填写推理的依据
证明:
因为AB∥CD( )
所以∠EPB=∠PQD( )
因为AB⊥EF( )
所以∠EPB=90 ( )
所以∠PQD=90 ( )
所以CD⊥EF( )
已知
Q
两直线平行,同位角相等
已知
方法技巧
逻辑链:
已知平行
→同位角相等
→已知垂直
→夹角90°
→等量代换
→结论垂直
垂直的定义
等量代换
垂直的定义
课堂练习
基础巩固
4.写出命题“等角的余角相等”的逆命题,并指出它的逆命题是真命题还是假命题。如果是真命题,请加以证明;如果是假命题,请举出反例。
解:逆命题为余角相等的两个角相等。逆命题是真命题,证明如下:
已知:∠1与∠3互为余角(∠1 + ∠3 = 90°),∠2与∠4互为余角(∠2 + ∠4 = 90°),且∠3 = ∠4。
求证:∠1 = ∠2。
因为∠1与∠3互为余角(已知)
所以∠1 = 90° - ∠3(余角的定义)
因为∠2与∠4互为余角(已知)
所以∠2 = 90° - ∠4(余角的定义)
因为∠3 = ∠4(已知)
所以90° - ∠3 = 90° - ∠4(等式的性质)
所以∠1 = ∠2(等量代换)
1
2
3
4
课堂练习
生活逻辑
几何证明
思路整理
互逆命题
真命题:逆定理(需证明)
假命题:举反例
核心概念 关键结论 典型案例
互逆命题定义 条件与结论互换生成新命题 平行线性质定理 vs 判定定理
逆命题的改写规则 严格交换条件与结论,语句通顺 “对顶角相等” → “相等的角是对顶角”
逆命题的真假独立性 原命题为真,逆命题未必为真(需独立证明) 理发师悖论的反例剖析
知识结构化
感谢聆听!
青岛版2024·八年级上册
1.3 几何证明举例
第一章
推理与证明
第1课时
互逆命题的推导与证明
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
如何证明
互逆命题的推导与证明
推论的意义与运用
反证法的证明范式
合情推理到逻辑推理
学 习 目 标
1
2
能够准确识别原命题与逆命题的条件、结论的互换特征,并能够规范书写给定命题的逆命题
掌握运用基本事实与定理进行演绎推理,证明互逆命题真假的方法
3
理解“原命题为真,逆命题未必成立”的核心逻辑,并会举反例判断逆命题的真假性
“若顾客不自己理发,则我为他理发”
情境导入
理发师的两难困局:逻辑规则的自我吞噬
小镇的理发师张贴新规:“我只给不自己理发的人理发”,某日,他正想给自己理发,却看着标识陷入了沉思…
“若我为他理发,则顾客自己不理发”
若理发,违反规则(只服务于“不理发的人”)
若不理发,属于“不理发的人”,应被服务
这个死循环的根源究竟是什么?
这个问题将在接下来互逆命题的学习中完美解决
情境导入
从生活悖论到几何证明——初步认识互逆关系
基本事实
性质定理Ⅰ
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
两条平行直线被第三条直线所截,同位角相等
条件: 两条直线被第三条直线所截,如果同位角相等
结论: 那么这两条直线平行
条件:两条平行直线被第三条直线所截
结论:同位角相等
条件与结论完全相反,互逆关系
可证明
以上基本事实与性质定理有何关系?
如何用它们证明平行线的其他性质何判定定理?
新知探究
平行线的性质定理Ⅱ:两条平行直线被第三条直线所截,内错角相等
(1)已知:如图 ,直线 AB//CD,直线 EF 分别交 AB,CD 于点 O 和 P
求证:∠AOP = ∠OPD
证明:因为 AB//CD(已知)
所以∠OPD = ∠EOB(两直线平行,同位角相等)
因为∠EOB = ∠AOP(对顶角相等)
所以∠AOP = ∠OPD(等量代换)
A
B
C
D
P
O
方法技巧
解决本题的关键在于将内错角转化为已知相等的角,并会使用到平行线的性质定理Ⅰ
E
F
新知探究
平行线的性质定理Ⅲ:两条平行直线被第三条直线所截,同旁内角互补
(2)已知:如图,直线AB//CD,直线EF分别交AB、CD于点O和P。
求证:∠AOP + ∠OPC = 180°
因为AB//CD(已知)
所以∠AOP = ∠OPD(两直线平行,内错角相等)
因为∠OPD + ∠OPC = 180°(平角的定义)
所以∠AOP + ∠OPC = 180°(等量代换)
因此,∠AOP与∠OPC互补(互补的定义)
B
C
P
方法技巧
解决本题的关键在于“转化思想”,通过同位角、对顶角等中间量,将未知的内错角转化为已知的相等角
新知探究
判定定理Ⅰ:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
(3)已知:如图1.3-2,直线EF分别交AB、CD于点O、P,∠AOP=∠OPD(内错角相等)
求证:AB//CD
证明:因为∠EOB=∠AOP(对顶角相等)
又因为∠AOP=∠OPD(已知)
所以∠EOB=∠OPD(等量代换)
因此AB//CD(同位角相等,两直线平行)
知识补充
容易发现,该判定定理与平行线的性质定理是互逆关系.二者的因果关系相反。
性质定理:用已知平行求角相等
判定定理:用已知角相等求平行
本条定理与平行线的性质定理Ⅱ对比,有什么联系?
新知探究
平行线的判定定理Ⅱ:两条直线被第三条直线所截,若同旁内角互补,那么这两条直线平行
本条定理与平行线的性质定理Ⅲ对比,条件与结论发生了什么变化?
(4)已知:直线截、于、,;
求证:AB//
证明:因为∠BOP+∠OPD=180°(已知)
又因为∠BOP+∠EOB=180°(邻补角的定义)
所以∠EOB=∠OPD(等量代换)
所以AB//CD(同位角相等,两直线平行)
知识补充
容易发现,该判定定理与平行线的性质定理Ⅲ,条件和结论完全相反。
知识小结
互逆命题与逆定理——从观察到定义的逻辑之旅
观察上面的(1)和(3),(2)和(4)中的两个命题,它们的条件和结论之间有什么关系?
第一个命题和第二个命题的结论和条件完全相反
概括与表达
互逆命题:
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题叫做互逆命题
逆命题:
如果把其中一个叫做原命题,那么另一个叫做逆命题
逆定理:
如果一个命题的逆命题也是真命题,那么这个逆命题叫做逆定理
原命题成立,逆命题一定成立吗?
即时小练
类型一:互逆命题的判断
1:下列各组命题中,互为逆命题的是( )
A. ① 如果a>0,那么a >0;② 如果a >0,那么a<0
B. ① 两直线平行,同位角相等;② 同位角相等,两直线平行
C. ① 如果x=3,那么x =9;② 如果x ≠9,那么x≠3
D. ① 对顶角相等;② 相等的角是对顶角
条件
结论
条件
结论
并非互逆关系
条件
互逆关系
条件:如果两个角是对顶角
结论:那么它们相等
结论:那么它们是对顶角
条件:如果两个角相等
并非互逆关系
方法技巧
互逆命题的唯一判断依据:两个命题的“条件”和“结论”是否互换(不涉及真假)
原命题:若(条件),则(结论)
逆命题:若(原命题的结论),则(原命题的条件)
即时小练
类型二:逆命题的改写与真假判断
2.写出下列命题的逆命题,并判断这些逆命题是真命题还是假命题。
(1)对顶角相等;
(2)在同一平面内,如果两条直线没有公共点,那么这两条直线平行。
方法技巧
改写逆命题的步骤:
①找出原命题的条件和结论
②将条件与结论互换位置
③调整语句表诉,使其通顺
解:(1)逆命题:如果两个角相等,那么这两个角是对顶角;
真假判断:假命题
(2)逆命题:在同一平面内,如果两条直线平行,那么这两条直线没有公共点;
真假判断:真命题
即时小练
类型三:逆命题的证明
3.已知∠1=∠2求证:∠3+∠4=180°
变式:已知∠3+∠4=180° 求证: ∠1=∠2
结论
条件
证明:因为∠1=∠2(已知)
与变式互为逆命题
与原题互为逆命题
证明:因为∠3+∠4=180°(已知)
所以AB//CD(同位角相等,两直线平行)
所以AB//CD(同旁内角互补,两直线平行)
所以∠3+∠4=180°(两直线平行,同旁内角互补)
所以∠1=∠2(两直线平行,同位角相等)
1
2
3
4
知识小结
原命题与逆命题的逻辑关系——原命题成立,逆命题不一定成立
理发师错误的认为原命题成立,逆命题就一定成立,因此陷入了逻辑困境
类型一与类型二中的题目
原命题成立,逆命题不一定成立
类型三的题目与变式
原命题与逆命题的真假性需要独立证明
回顾情境,你能理解理发师的逻辑困境了吗?
概括与表达
逆命题的正确性需独立判断,不能默认与原命题一致
课堂练习
1.命题“如果两个角是直角,那么它们相等”的逆命题是( )
A.如果两个角相等,那么它们是直角
B. 如果两个角不是直角,那么它们不相等
C. 如果两个角不相等,那么它们不是直角
D. 两个相等的角是直角
基础巩固
条件
结论
逆命题:如果(结论),那么(条件)
综上,答案选A
方法技巧
找逆命题的核心操作就是:
严格交换“条件(p)”和“结论(q)”,且条件和结论在交换后不能发生实际意义上的变化
课堂练习
基础巩固
2.写出下列命题的逆命题,并判断这些逆命题的真假
(1)如果两个角相等,那么这两个角的补角相等;
(2)两条直线被第三条直线所截,如果同位角相等,那么内错角相等。
解:(1)逆命题:如果两个角的补角相等,那么这两个角相等;
真假判断:真命题
(2)逆命题:两条直线被第三条直线所截,如果内错角相等,那么同位角相等;
真假判断:真命题
方法技巧
逆命题的真假需要独立判断,本题两个逆命题都为真,但并非所有逆命题都为真
课堂练习
基础巩固
3. 阅读证明过程,并在括号内填写推理的依据
证明:
因为AB∥CD( )
所以∠EPB=∠PQD( )
因为AB⊥EF( )
所以∠EPB=90 ( )
所以∠PQD=90 ( )
所以CD⊥EF( )
已知
Q
两直线平行,同位角相等
已知
方法技巧
逻辑链:
已知平行
→同位角相等
→已知垂直
→夹角90°
→等量代换
→结论垂直
垂直的定义
等量代换
垂直的定义
课堂练习
基础巩固
4.写出命题“等角的余角相等”的逆命题,并指出它的逆命题是真命题还是假命题。如果是真命题,请加以证明;如果是假命题,请举出反例。
解:逆命题为余角相等的两个角相等。逆命题是真命题,证明如下:
已知:∠1与∠3互为余角(∠1 + ∠3 = 90°),∠2与∠4互为余角(∠2 + ∠4 = 90°),且∠3 = ∠4。
求证:∠1 = ∠2。
因为∠1与∠3互为余角(已知)
所以∠1 = 90° - ∠3(余角的定义)
因为∠2与∠4互为余角(已知)
所以∠2 = 90° - ∠4(余角的定义)
因为∠3 = ∠4(已知)
所以90° - ∠3 = 90° - ∠4(等式的性质)
所以∠1 = ∠2(等量代换)
1
2
3
4
课堂练习
生活逻辑
几何证明
思路整理
互逆命题
真命题:逆定理(需证明)
假命题:举反例
核心概念 关键结论 典型案例
互逆命题定义 条件与结论互换生成新命题 平行线性质定理 vs 判定定理
逆命题的改写规则 严格交换条件与结论,语句通顺 “对顶角相等” → “相等的角是对顶角”
逆命题的真假独立性 原命题为真,逆命题未必为真(需独立证明) 理发师悖论的反例剖析
知识结构化
感谢聆听!
同课章节目录
