1.3几何证明举例(第2课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册
文档属性
| 名称 | 1.3几何证明举例(第2课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 07:55:52 | ||
图片预览




文档简介
(共20张PPT)
青岛版2024·八年级上册
1.3 几何证明举例
第一章
推理与证明
1.3.2 推论的意义与运用
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
如何证明
互逆命题的推导与证明
推论的意义与运用
反证法的证明范式
合情推理到逻辑推理
学 习 目 标
1
2
明确区分定理与推论的逻辑关系
掌握“由定理直接推出推论”的演绎方法
3
能够运用推论简化证明过程,迁移推理方法解决新问题
情境导入
希帕索斯的“无理”之死——推论的不可反驳性
毕达哥拉斯学派奉行“万物皆整数比”的理念
认为一切数都可以表示成整数或两个整数之比。
但学生希帕索斯从勾股定理()得出这样一个推论:
边长为1的正方形对角线()无法表示为整数比
这个由勾股定理推出来的“”,让学派内的所有信徒和学生都没办法推翻它是无理数的事实
情境导入
希帕索斯的“无理”之死——推论的不可反驳性
但“”是无理数这一推论却始终无法反驳,由此引发了“第一次数学危机”
这激怒了毕达哥拉斯学派,他们以“背叛”罪名判处希帕索斯死刑
那么数学推论到底是什么?它有什么意义和用途?
今天我们将从“三角形的内角和”定理出发
看它会诞生出何种“危险推论”,同时探索推论的意义。
新知探究
“三角形内角和”定理的证明
【回顾】上学期,我们从基本事实(如平角定义、平行线性质)出发,说明了“三角形的内角和等于180°”的正确性。
怎样严格证明“三角形的内角和等于180°”呢?
【思考与交流】
证明:三角形的内角和等于180°。
已知:如图,∠A、∠B、∠C是△ABC的三个内角。
求证:∠A + ∠B + ∠C = 180°。
提示:
(1)通过“剪拼法”可将三个角拼为平角(上学期实验方法);
(2)类似地,我们可以通过“作平行线”(辅助线),将角“转移”到同一顶点,利用平行线性质实现证明。
A
B
C
新知探究
“三角形内角和”定理的证明
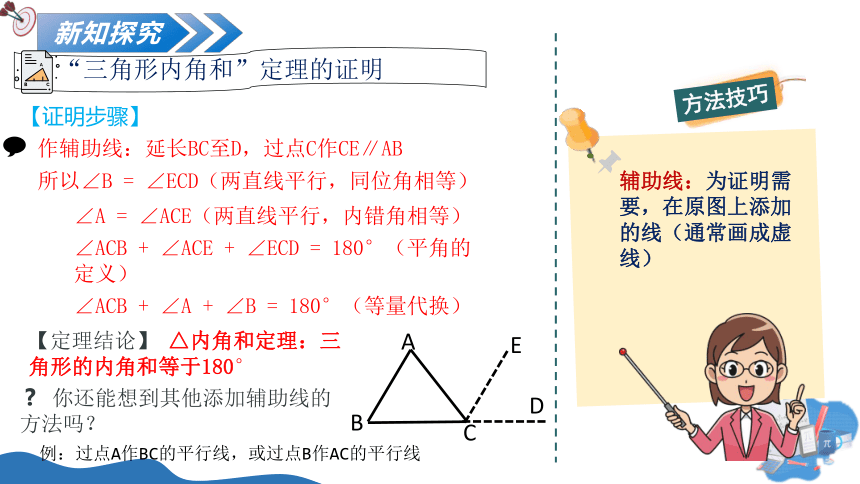
【证明步骤】
A
C
B
作辅助线:延长BC至D,过点C作CE∥AB
所以∠B = ∠ECD(两直线平行,同位角相等)
∠A = ∠ACE(两直线平行,内错角相等)
∠ACB + ∠ACE + ∠ECD = 180°(平角的定义)
∠ACB + ∠A + ∠B = 180°(等量代换)
D
E
【定理结论】 △内角和定理:三角形的内角和等于180°
方法技巧
辅助线:为证明需要,在原图上添加的线(通常画成虚线)
你还能想到其他添加辅助线的方法吗?
例:过点A作BC的平行线,或过点B作AC的平行线
新知探究
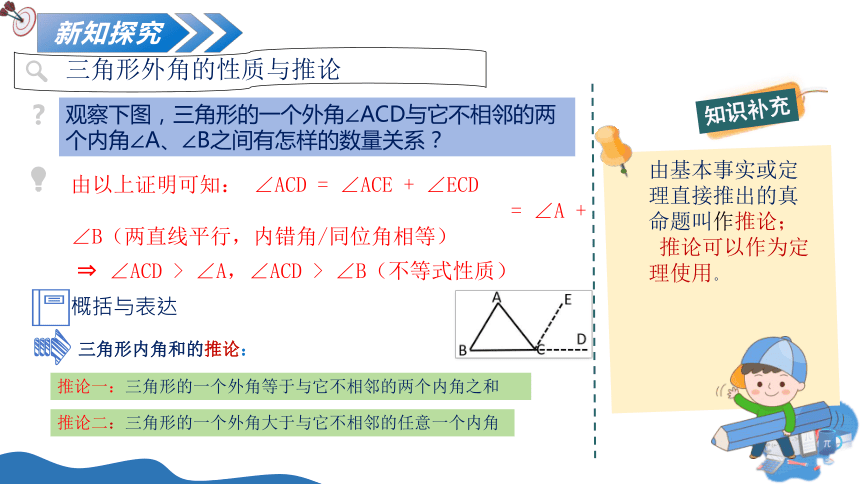
三角形外角的性质与推论
观察下图,三角形的一个外角∠ACD与它不相邻的两个内角∠A、∠B之间有怎样的数量关系?
由以上证明可知: ∠ACD = ∠ACE + ∠ECD
= ∠A + ∠B(两直线平行,内错角/同位角相等)
∠ACD > ∠A,∠ACD > ∠B(不等式性质)
概括与表达
三角形内角和的推论:
推论一:三角形的一个外角等于与它不相邻的两个内角之和
推论二:三角形的一个外角大于与它不相邻的任意一个内角
知识补充
由基本事实或定理直接推出的真命题叫作推论;
推论可以作为定理使用。
新知探究
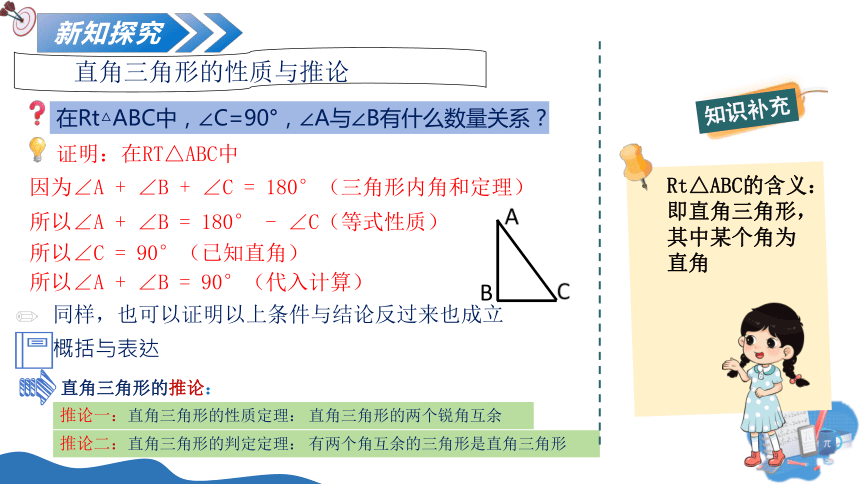
直角三角形的性质与推论
在Rt△ABC中,∠C=90°,∠A与∠B有什么数量关系?
证明:在RT△ABC中
因为∠A + ∠B + ∠C = 180°(三角形内角和定理)
所以∠A + ∠B = 180° - ∠C(等式性质)
所以∠C = 90°(已知直角)
所以∠A + ∠B = 90°(代入计算)
同样,也可以证明以上条件与结论反过来也成立
概括与表达
直角三角形的推论:
推论一:直角三角形的性质定理: 直角三角形的两个锐角互余
推论二:直角三角形的判定定理: 有两个角互余的三角形是直角三角形
B
知识补充
Rt△ABC的含义:
即直角三角形,其中某个角为直角
知识小结
推论的辨析
知识总结:推论与定理的区别
维度 定理(如三角形内角和定理) 推论(如外角性质/直角互余)
定义
依赖关系
推导过程
地位作用
经严格证明的核心真命题
由定理/基本事实直接推出的真命题
不依赖其他定理(依赖公理/基本事实)
必须依赖已有定理(如内角和定理)
复杂(多步辅助线/公理组合,如作平行线证内角和)
简单(1-2步推导,如外角=180°-内角和)
数学体系的“地基”,可推导多个推论
定理的“延伸应用”,直接服务解题
推论是定理的逻辑延伸,推理是连接“已知”与“未知”的桥梁。 无论是定理还是推论,都是数学严谨性的体现!
新知探究
推论的实际运用
已知:在△ABC中,∠B=∠C,D是BC边上一点;过点D作 DE⊥AB,DF⊥BC,垂足分别为E、D。
求证:∠FDE=∠C。
A
B
C
D
E
F
证明:
因为DE⊥AB,DF⊥BC(已知)
所以∠DEB=90°,∠FDC=90°(垂直的定义)
因为∠EDC是△EBD的外角(外角定义)
所以∠EDC=∠B+∠DEB(三角形的外角=不相邻两内角和)
因为∠EDC=∠FDE+∠FDC(已知)
所以∠FDE+∠FDC=∠B+∠DEB(等量代换)
所以∠FDE+90°=∠B+90°(等量代换)
因为∠B=∠C(已知)
所以∠FDE=∠C(等量代换)
本题中,我们使用了三角形内角和的推论,想想要是不用词条推论,会多多少条步骤 你能总结推论的意义吗
知识小结
推论的意义
概括与表达
推论的意义:
1.**知识延伸的捷径**:从定理“生长”出新结论,避免重复证明
(如外角性质直接用内角和推导)
2.**解题效率的提升**:推论作为“半成品工具”,简化复杂问题
(如用互余性质快速求直角三角形锐角)
3.**逻辑思维的训练**:体会“定理→推论”的严谨链条,培养“言必有据”的推理习惯
通过情境中希帕索斯的故事我们可以知道,推论还具有不可反驳性,下面就让我们体会合理运用定理与推论是如何简化证明过程的
即时训练
合理使用定理简化证明过程
1.证明:四边形四个内角的和等于360°。
已知:如图,∠A、∠B、∠C,∠D是四边形ABCD的四个内角。
求证:∠BAD + ∠B + ∠BCD +∠D=360°
证明:连接AC,可得△ ABC与△ ACD
B
所以∠B+∠BAC+∠ACB=180°,∠D+∠DAC+∠DCA=180°(三角形内角和定理)
因为∠BAD=∠BAC+∠DAC,
∠BCD=∠BCA+∠DCA(角的和的定义)
所以∠BAD + ∠B + ∠BCD +∠D=180°+180°=360°(等量代换)
知识补充
使用三角形的内角和定理使得本题的证明过程大大减少,同样的,可以证明出多边形内角和为:
(n-2)180°
即时训练
合理使用推论简化证明过程
2. 已知:如图,在Rt△ABC中,∠ACB=90 ,CD⊥AB,垂足为点D
求证:∠1=∠B
1
证明:因为∠ACB=90°(已知)
所以∠A + ∠B = 90°(直角三角形两锐角互余)
因为CD⊥AB(已知)
所以∠ADC=90°(垂直定义)
所以∠A + ∠1 = 90°(直角三角形两锐角互余)
所以∠1 = ∠B(同角的余角相等)
本题证明合理的使用了直角三角形的推论,让证明过程得到简化;同时还用到相关的定理,使得本题证明过程更加严谨。
方法技巧
即时训练
合理使用推论简化证明过程
3. 已知:如图,D是△ABC内一点,连接DB、DC。
求证:∠BDC>∠A
E
证明:延长BD交AC于E(构造外角)
因为∠BDC是△CDE的外角(外角定义)
所以∠BDC > ∠DEC(三角形外角大于不相邻内角)
因为∠DEC是△ABE的外角(外角定义)
所以∠DEC > ∠A(三角形外角大于不相邻内角)
所以∠BDC > ∠A(不等式传递性)
方法技巧
此题的证明逻辑链如下:
构造辅助线→用外角定理建立不等关系→通过中间角传递不等
在这个过程中,容易发现,使用三角形内角和的推论极大的简化了证明过程,也使得证明过程更加严谨
课堂练习
一、填空
第2题证明“∠1=∠B”时,两次用到“直角三角形两锐角互余”,该结论是由“______________________”(填定理名称)直接推出的,因此它是该定理的________(填“定理”或“推论”)。
第3题证明“∠BDC>∠A”的关键依据是“三角形的外角大于任何一个不相邻的内角”,该结论是“________________”(填定理名称)的推论,其作用是__________________________(填推论的意义,如“简化角的大小关系证明”)。
三角形内角和定理
推论
三角形内角和定理
直接建立不相邻角的大小关系
方法技巧
推论不是孤立的结论,而是定理的“快捷应用工具”,其核心意义在于简化推理过程,提升解题效率。
课堂练习
2.(即时训练变式)在第2题图中,已知Rt△ABC中∠ACB=90°,CD⊥AB,若∠A=40°,仅用“直角三角形两锐角互余”这一推论,求∠1和∠B的度数,并说明推论如何简化计算。
提示:在前面证明∠1=∠B时,不仅仅用到了“直角三角形的两锐角互余”这一推论,还用到了“等角的余角相等”这一定理
解:在Rt△ABC中,∠B=90°-∠A=50°(直角三角形两锐角互余推论)
在Rt△ACD中,∠1=90°-∠A=50°(直角三角形两锐角互余推论)
简化意义:直接用推论得出结果,无需重新计算三角形内角和。
方法技巧
通用结论:在Rt△ABC中,CD⊥AB(双垂直模型),则: ① ∠1=∠B,∠2=∠A(每组锐角对应相等,均由“同角的余角相等”推导)
课堂练习
已知: ① ∠ACE是△ABC的外角; ② BD平分∠ABC,CD平分∠ACE。
求证: ∠D = ∠A。
E
F
因为 BD平分∠ABC(已知)
所以 ∠DBC = ∠ABC,同理∠DCE = ∠ACE(角平分线定义)
因为 ∠ACE是△ABC的外角(已知)
所以 ∠D = ∠DCE - ∠DBC(等式变形)
= ∠ACE - ∠ABC
= (∠A + ∠ABC - ∠ABC) (等量代换)
所以 ∠ACE = ∠A + ∠ABC,同理∠DCE = ∠DBC + ∠D(三角形的外角和定理)
= ∠A(化简)
方法技巧
运用两次外角和推论,是连接已知与未知的桥梁,极大的简化了证明过程
课堂总结
1. 推论是什么?
由已知定理直接推出的真命题,但依赖于已有的定理(无需重新证明)
2. 推论的意义
简化证明流程
建立“已知”与“未知”的桥梁
3.推论的运用逻辑
优先用推论:如看到三角形外角,立即想到“外角定理”(不用内角和重新推导)
进行代数化简:如用推论结果消去中间角,快速得结论。
可结合其他定理:如将分角转化为原角的一半,便于代入
感谢聆听!
青岛版2024·八年级上册
1.3 几何证明举例
第一章
推理与证明
1.3.2 推论的意义与运用
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
如何证明
互逆命题的推导与证明
推论的意义与运用
反证法的证明范式
合情推理到逻辑推理
学 习 目 标
1
2
明确区分定理与推论的逻辑关系
掌握“由定理直接推出推论”的演绎方法
3
能够运用推论简化证明过程,迁移推理方法解决新问题
情境导入
希帕索斯的“无理”之死——推论的不可反驳性
毕达哥拉斯学派奉行“万物皆整数比”的理念
认为一切数都可以表示成整数或两个整数之比。
但学生希帕索斯从勾股定理()得出这样一个推论:
边长为1的正方形对角线()无法表示为整数比
这个由勾股定理推出来的“”,让学派内的所有信徒和学生都没办法推翻它是无理数的事实
情境导入
希帕索斯的“无理”之死——推论的不可反驳性
但“”是无理数这一推论却始终无法反驳,由此引发了“第一次数学危机”
这激怒了毕达哥拉斯学派,他们以“背叛”罪名判处希帕索斯死刑
那么数学推论到底是什么?它有什么意义和用途?
今天我们将从“三角形的内角和”定理出发
看它会诞生出何种“危险推论”,同时探索推论的意义。
新知探究
“三角形内角和”定理的证明
【回顾】上学期,我们从基本事实(如平角定义、平行线性质)出发,说明了“三角形的内角和等于180°”的正确性。
怎样严格证明“三角形的内角和等于180°”呢?
【思考与交流】
证明:三角形的内角和等于180°。
已知:如图,∠A、∠B、∠C是△ABC的三个内角。
求证:∠A + ∠B + ∠C = 180°。
提示:
(1)通过“剪拼法”可将三个角拼为平角(上学期实验方法);
(2)类似地,我们可以通过“作平行线”(辅助线),将角“转移”到同一顶点,利用平行线性质实现证明。
A
B
C
新知探究
“三角形内角和”定理的证明
【证明步骤】
A
C
B
作辅助线:延长BC至D,过点C作CE∥AB
所以∠B = ∠ECD(两直线平行,同位角相等)
∠A = ∠ACE(两直线平行,内错角相等)
∠ACB + ∠ACE + ∠ECD = 180°(平角的定义)
∠ACB + ∠A + ∠B = 180°(等量代换)
D
E
【定理结论】 △内角和定理:三角形的内角和等于180°
方法技巧
辅助线:为证明需要,在原图上添加的线(通常画成虚线)
你还能想到其他添加辅助线的方法吗?
例:过点A作BC的平行线,或过点B作AC的平行线
新知探究
三角形外角的性质与推论
观察下图,三角形的一个外角∠ACD与它不相邻的两个内角∠A、∠B之间有怎样的数量关系?
由以上证明可知: ∠ACD = ∠ACE + ∠ECD
= ∠A + ∠B(两直线平行,内错角/同位角相等)
∠ACD > ∠A,∠ACD > ∠B(不等式性质)
概括与表达
三角形内角和的推论:
推论一:三角形的一个外角等于与它不相邻的两个内角之和
推论二:三角形的一个外角大于与它不相邻的任意一个内角
知识补充
由基本事实或定理直接推出的真命题叫作推论;
推论可以作为定理使用。
新知探究
直角三角形的性质与推论
在Rt△ABC中,∠C=90°,∠A与∠B有什么数量关系?
证明:在RT△ABC中
因为∠A + ∠B + ∠C = 180°(三角形内角和定理)
所以∠A + ∠B = 180° - ∠C(等式性质)
所以∠C = 90°(已知直角)
所以∠A + ∠B = 90°(代入计算)
同样,也可以证明以上条件与结论反过来也成立
概括与表达
直角三角形的推论:
推论一:直角三角形的性质定理: 直角三角形的两个锐角互余
推论二:直角三角形的判定定理: 有两个角互余的三角形是直角三角形
B
知识补充
Rt△ABC的含义:
即直角三角形,其中某个角为直角
知识小结
推论的辨析
知识总结:推论与定理的区别
维度 定理(如三角形内角和定理) 推论(如外角性质/直角互余)
定义
依赖关系
推导过程
地位作用
经严格证明的核心真命题
由定理/基本事实直接推出的真命题
不依赖其他定理(依赖公理/基本事实)
必须依赖已有定理(如内角和定理)
复杂(多步辅助线/公理组合,如作平行线证内角和)
简单(1-2步推导,如外角=180°-内角和)
数学体系的“地基”,可推导多个推论
定理的“延伸应用”,直接服务解题
推论是定理的逻辑延伸,推理是连接“已知”与“未知”的桥梁。 无论是定理还是推论,都是数学严谨性的体现!
新知探究
推论的实际运用
已知:在△ABC中,∠B=∠C,D是BC边上一点;过点D作 DE⊥AB,DF⊥BC,垂足分别为E、D。
求证:∠FDE=∠C。
A
B
C
D
E
F
证明:
因为DE⊥AB,DF⊥BC(已知)
所以∠DEB=90°,∠FDC=90°(垂直的定义)
因为∠EDC是△EBD的外角(外角定义)
所以∠EDC=∠B+∠DEB(三角形的外角=不相邻两内角和)
因为∠EDC=∠FDE+∠FDC(已知)
所以∠FDE+∠FDC=∠B+∠DEB(等量代换)
所以∠FDE+90°=∠B+90°(等量代换)
因为∠B=∠C(已知)
所以∠FDE=∠C(等量代换)
本题中,我们使用了三角形内角和的推论,想想要是不用词条推论,会多多少条步骤 你能总结推论的意义吗
知识小结
推论的意义
概括与表达
推论的意义:
1.**知识延伸的捷径**:从定理“生长”出新结论,避免重复证明
(如外角性质直接用内角和推导)
2.**解题效率的提升**:推论作为“半成品工具”,简化复杂问题
(如用互余性质快速求直角三角形锐角)
3.**逻辑思维的训练**:体会“定理→推论”的严谨链条,培养“言必有据”的推理习惯
通过情境中希帕索斯的故事我们可以知道,推论还具有不可反驳性,下面就让我们体会合理运用定理与推论是如何简化证明过程的
即时训练
合理使用定理简化证明过程
1.证明:四边形四个内角的和等于360°。
已知:如图,∠A、∠B、∠C,∠D是四边形ABCD的四个内角。
求证:∠BAD + ∠B + ∠BCD +∠D=360°
证明:连接AC,可得△ ABC与△ ACD
B
所以∠B+∠BAC+∠ACB=180°,∠D+∠DAC+∠DCA=180°(三角形内角和定理)
因为∠BAD=∠BAC+∠DAC,
∠BCD=∠BCA+∠DCA(角的和的定义)
所以∠BAD + ∠B + ∠BCD +∠D=180°+180°=360°(等量代换)
知识补充
使用三角形的内角和定理使得本题的证明过程大大减少,同样的,可以证明出多边形内角和为:
(n-2)180°
即时训练
合理使用推论简化证明过程
2. 已知:如图,在Rt△ABC中,∠ACB=90 ,CD⊥AB,垂足为点D
求证:∠1=∠B
1
证明:因为∠ACB=90°(已知)
所以∠A + ∠B = 90°(直角三角形两锐角互余)
因为CD⊥AB(已知)
所以∠ADC=90°(垂直定义)
所以∠A + ∠1 = 90°(直角三角形两锐角互余)
所以∠1 = ∠B(同角的余角相等)
本题证明合理的使用了直角三角形的推论,让证明过程得到简化;同时还用到相关的定理,使得本题证明过程更加严谨。
方法技巧
即时训练
合理使用推论简化证明过程
3. 已知:如图,D是△ABC内一点,连接DB、DC。
求证:∠BDC>∠A
E
证明:延长BD交AC于E(构造外角)
因为∠BDC是△CDE的外角(外角定义)
所以∠BDC > ∠DEC(三角形外角大于不相邻内角)
因为∠DEC是△ABE的外角(外角定义)
所以∠DEC > ∠A(三角形外角大于不相邻内角)
所以∠BDC > ∠A(不等式传递性)
方法技巧
此题的证明逻辑链如下:
构造辅助线→用外角定理建立不等关系→通过中间角传递不等
在这个过程中,容易发现,使用三角形内角和的推论极大的简化了证明过程,也使得证明过程更加严谨
课堂练习
一、填空
第2题证明“∠1=∠B”时,两次用到“直角三角形两锐角互余”,该结论是由“______________________”(填定理名称)直接推出的,因此它是该定理的________(填“定理”或“推论”)。
第3题证明“∠BDC>∠A”的关键依据是“三角形的外角大于任何一个不相邻的内角”,该结论是“________________”(填定理名称)的推论,其作用是__________________________(填推论的意义,如“简化角的大小关系证明”)。
三角形内角和定理
推论
三角形内角和定理
直接建立不相邻角的大小关系
方法技巧
推论不是孤立的结论,而是定理的“快捷应用工具”,其核心意义在于简化推理过程,提升解题效率。
课堂练习
2.(即时训练变式)在第2题图中,已知Rt△ABC中∠ACB=90°,CD⊥AB,若∠A=40°,仅用“直角三角形两锐角互余”这一推论,求∠1和∠B的度数,并说明推论如何简化计算。
提示:在前面证明∠1=∠B时,不仅仅用到了“直角三角形的两锐角互余”这一推论,还用到了“等角的余角相等”这一定理
解:在Rt△ABC中,∠B=90°-∠A=50°(直角三角形两锐角互余推论)
在Rt△ACD中,∠1=90°-∠A=50°(直角三角形两锐角互余推论)
简化意义:直接用推论得出结果,无需重新计算三角形内角和。
方法技巧
通用结论:在Rt△ABC中,CD⊥AB(双垂直模型),则: ① ∠1=∠B,∠2=∠A(每组锐角对应相等,均由“同角的余角相等”推导)
课堂练习
已知: ① ∠ACE是△ABC的外角; ② BD平分∠ABC,CD平分∠ACE。
求证: ∠D = ∠A。
E
F
因为 BD平分∠ABC(已知)
所以 ∠DBC = ∠ABC,同理∠DCE = ∠ACE(角平分线定义)
因为 ∠ACE是△ABC的外角(已知)
所以 ∠D = ∠DCE - ∠DBC(等式变形)
= ∠ACE - ∠ABC
= (∠A + ∠ABC - ∠ABC) (等量代换)
所以 ∠ACE = ∠A + ∠ABC,同理∠DCE = ∠DBC + ∠D(三角形的外角和定理)
= ∠A(化简)
方法技巧
运用两次外角和推论,是连接已知与未知的桥梁,极大的简化了证明过程
课堂总结
1. 推论是什么?
由已知定理直接推出的真命题,但依赖于已有的定理(无需重新证明)
2. 推论的意义
简化证明流程
建立“已知”与“未知”的桥梁
3.推论的运用逻辑
优先用推论:如看到三角形外角,立即想到“外角定理”(不用内角和重新推导)
进行代数化简:如用推论结果消去中间角,快速得结论。
可结合其他定理:如将分角转化为原角的一半,便于代入
感谢聆听!
同课章节目录
