1.3几何证明举例(第3课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册
文档属性
| 名称 | 1.3几何证明举例(第3课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 08:00:16 | ||
图片预览




文档简介
(共20张PPT)
青岛版2024·八年级上册
1.3 几何证明举例
第一章
推理与证明
1.3.3 反证法的证明范式
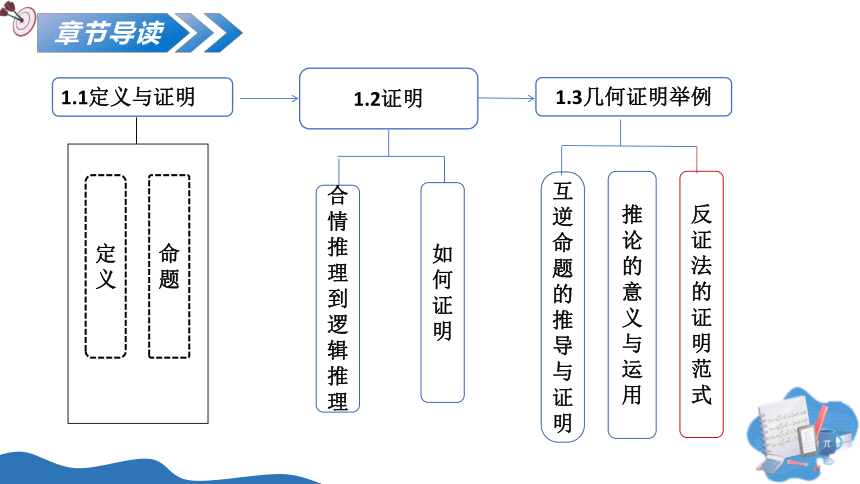
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
如何证明
互逆命题的推导与证明
推论的意义与运用
反证法的证明范式
合情推理到逻辑推理
学 习 目 标
1
2
能复述反证法三步骤:① 假设命题不成立 → ② 推导矛盾 → ③ 原命题成立
能辨别反证法使用场景(存在性、唯一性、无限性命题)
3
能用反证法完成经典证明
情境导入
第五公设:一场两千年的几何战争
阿
基
米
德
→
牛顿
全军覆没!
两千年前,欧几里得写下第五公设——主要说明过一点有且只有一条直线与已知直线平行!一时之间,所有数学家都想证明这个又长又怪的公设
俄罗斯‘几何狂人’罗巴切夫斯基: 既然证明不了,不如彻底造反!
假设过一点→两条平行线!
然而若是该假设成立,竟会发现三角形的内角和小于180°
情境导入
反证法:在荒谬中炸出新宇宙
如此荒谬的假设,你会认同吗?
不!他用反证法挖出了新宇宙 罗氏几何! 爱因斯坦用此推翻牛顿引力,重塑时空!
反证法究竟有何等威力 能把把‘不可能’变成新世界的基石?
接下来,让我们走进课堂,了解什么是反证法!如何使用反证法!
新知探究
反证法——当直接证明“走不通”时的思维突围
当一个命题从已知条件出发不易直接证得结论时,还有其他方法吗?
思考与交流
1
2
∠1=∠2
你常用的直接证明方法是什么?
试试用“新方法”证明熟悉的定理
证明平行线的性质定理Ⅰ:
两条平行直线被第三条直线所截,同位角相等
提示:
如果“假设同位角不相等”,会发生什么?
案例解析:用反证法证明平行线同位角相等
新知探究
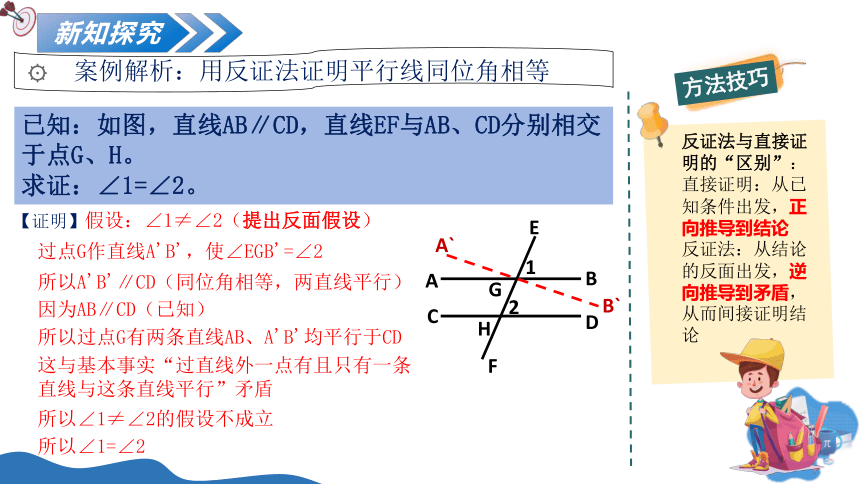
已知:如图,直线AB∥CD,直线EF与AB、CD分别相交于点G、H。
求证:∠1=∠2。
【证明】
假设:∠1≠∠2(提出反面假设)
过点G作直线A'B',使∠EGB'=∠2
所以A'B'∥CD(同位角相等,两直线平行)
因为AB∥CD(已知)
所以过点G有两条直线AB、A'B'均平行于CD
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾
所以∠1≠∠2的假设不成立
所以∠1=∠2
A
C
B
D
E
F
G
H
A`
B`
1
2
方法技巧
反证法与直接证明的“区别”:
直接证明:从已知条件出发,正向推导到结论
反证法:从结论的反面出发,逆向推导到矛盾,从而间接证明结论
知识小结
反证法:从“假设反面”到“证明结论”的逻辑闭环
以上这种证明方法有怎样的特点?它包括了哪几个步骤?
反证法的核心特点
- **间接性**:不直接证明结论,而是通过“否定反面”间接验证;
概括与表达
- **矛盾性**:核心是“推导矛盾”(与已知条件、定理冲突)
- **逻辑性**:严格遵循“假设→推导→结论”的闭环,无逻辑漏洞。
反证法的三步流程
① **否定结论**
假设命题的结论不成立
② **推出矛盾**
从假设出发,结合已知条件,推导出自相矛盾的结果
③ **肯定结论**
由矛盾判定假设不成立,从而证明原结论
**反证法**:提出与命题的结论相反的假设,再从假设出发推出矛盾,从而证明命题成立的方法
新知探究
情境一:“以有证无”,反证法破解否定性命题的核心逻辑
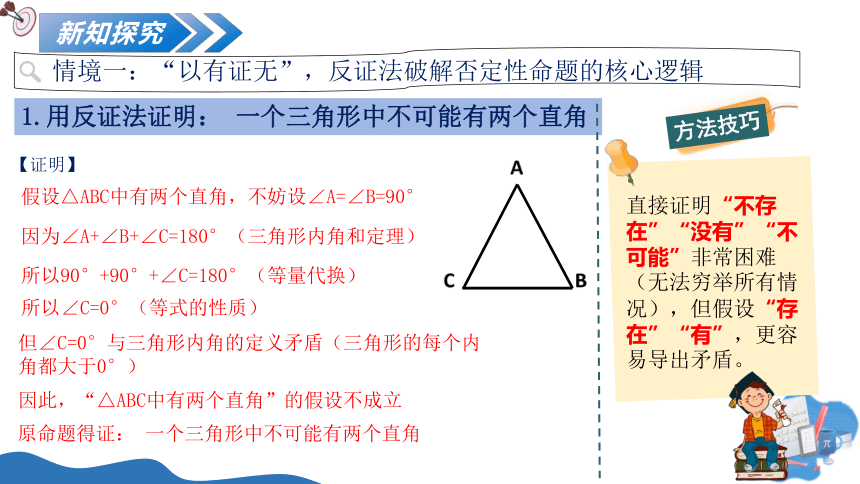
1.用反证法证明: 一个三角形中不可能有两个直角
假设△ABC中有两个直角,不妨设∠A=∠B=90°
因为∠A+∠B+∠C=180°(三角形内角和定理)
所以90°+90°+∠C=180°(等量代换)
所以∠C=0°(等式的性质)
但∠C=0°与三角形内角的定义矛盾(三角形的每个内角都大于0°)
因此,“△ABC中有两个直角”的假设不成立
【证明】
原命题得证: 一个三角形中不可能有两个直角
方法技巧
直接证明“不存在”“没有”“不可能”非常困难(无法穷举所有情况),但假设“存在”“有”,更容易导出矛盾。
新知探究
情景二:反证法破“至少/至多”题:从“全反假设”到“矛盾突破”
2.用反证法证明:在直角三角形中,至少有一个锐角不大于45°
已知:设直角三角形ABC中,∠C=90°
求证:∠A或∠B中至少有一个≤45°
【证明】假设∠A>45°,∠B>45°
因为∠A+∠B+∠C=180°(三角形的内角和定理)
且∠C=90°(已知)
所以∠A+∠B=90°(等量代换,等式的性质)
因为∠A>45°且∠B>45°(已知)
所以∠A+∠B>45°+45°=90°
这与∠A+∠B=90°矛盾
所以假设不成立,原命题得证
方法技巧
(1)“至少一个”的反面是“全不”(如“至少有一个锐角≤45°”的反面是“所有锐角都>45°”);
(2)“至多一个”的反面是“至少两个”(如“至多有一个直角”的反面是“有两个或更多直角”)
新知探究
情景三:反证法破“唯一性”命题,用“多”的假设,证“一”的必然
3.平行公理——过直线外一点只有一条直线与已知直线平行
已知:直线l,点P在l外;
求证:过P只有一条直线与l平行
证明:假设过P有两条直线 、都平行于l( )
因为 //l, //l,且 (已知)
所以 (平行线的传递性)
因为 、都过点P(已知)
所以 ,即二者重合(两点确定一条直线的基本事实)
这与假设矛盾,假设不成立,原命题得证。
P
l
方法技巧
直接证明“只有一个”需要排除所有其他可能,而假设“有两个或更多”,更容易通过逻辑推导矛盾(如与定义、定理冲突)。
知识小结
反证法的适用情境归纳
核心逻辑
反证法的本质是 “否定反面→推导矛盾→肯定原结论”,适用于直接证明困难的命题
四大适用情境
1. 否定性命题
特点:证明“不存在”“不可能”“没有”
2. 唯一性命题
特点:证明“唯一”“只有一个”“有且仅有”
3. “至少/至多”类命题
特点:证明“至少有一个”“至多有一个”
4. 难以直接构造的命题
特点:无法通过直接举例或正向推导证明
证明的方法主要有两种:直接证明与间接证明,而“反证法”就是间接证明的典型方法
课堂练习
1.下列关于反证法证明平行公理的步骤, 顺序正确 的是( )
① 两条直线都过P且平行,必重合;
② 假设过P有两条不同直线与l平行;
③ 假设不成立,原命题得证;
④ 由平行传递性得两条直线平行。
A. ②→④→①→③
B. ①→②→③→④
C. ③→②→①→④
D. ②→①→④→③
导出矛盾
假设反面
得出结论
推导过程
答案解析:假设推导矛盾是反证法解答的一般过程,故选A
方法技巧
反证法的核心流程是“假设→推导→矛盾→结论”
课堂练习
2. 用反证法证明“三角形中不可能有两个钝角”时, 推导过程中导出的矛盾 是( )
A.与“三角形内角和为180°”矛盾
B. 与“钝角的定义(大于90°)”矛盾
C. 与“平行线性质”矛盾
D. 与“线段中点的定义”矛盾
否定性命题
【解】
否定性命题,该将“不可能”假设为“必然”
假设三角形中有两个钝角(设为∠A>90°,∠B>90°),则∠A+∠B>180°
加上第三个角∠C>0°,三角形内角和∠A+∠B+∠C>180°
与“三角形内角和为180°”的定理矛盾,故选择A。
方法技巧
解题关键:
能够对要进行的命题进行假设,根据假设的内容推导出与之相对应的矛盾
课堂练习
3.下列命题中,最适合用反证法证明的是:( )
三角形的内角和为180° B. 是无理数
C. 二次函数的图像是抛物线 D. 直角三角形的勾股定理
性质定理
无法正向推导的命题
性质定理
性质定理
【解】
在以上四个选项中,性质定理都可以通过正向推理得出,但“ 是无理数 ”是难以正向推导的命题,故选B
方法技巧
解答关键:
能清楚的了解“反证法使用的四大场景”
1.否定性命题
2.唯一性命题
3.“至多/至少”类命题
4.无法正向推导的命题
课堂练习
用反证法证明:三角形的三个内角中,至少有一个内角大于或等于60°
已知:△ABC是任意三角形;
求证:∠A,∠B,∠C中至少有一个≥60°
证明:假设△ABC的三个内角都小于60°,即∠A<60°,∠B<60°,∠C<60°
因为∠A+∠B+∠C<60°+60°+60°=180°(三角形内角和定理)
所以∠A+∠B+∠C<180°与三角形内角和定理(∠A+∠B+∠C=180°)矛盾
所以,“三个内角都小于60°”的假设不成立,原结论得证
本题核心逻辑:
假设反面(都<60°)→推导(和<180°)
→矛盾(与内角和定理冲突)
→肯定原结论(至少一个≥60°)
方法技巧
课堂练习
用反证法证明:
已知:a+b>0
求证:a,b中至少有一个大于零。
假设a,b都不大于零,即a≤0且b≤0
所以a+b≤0+0=0(不等式加法性质)
因为a+b≤0与已知条件a+b>0矛盾
所以“a,b都不大于零”的假设不成立
原结论得证: a。b中至少有一个大于零
证明:
经过以上的练习,你对推理与证明的过程与方法是否完全熟悉了?
现在我们已经掌握了证明题的证明步骤,也对证明的方法和过程进行了深入的学习,那么证明题的完整逻辑流程是什么呢?
知识小结
证明题的逻辑流程
准备阶段
- 核心命题
- 隐含条件
策略选择
- 直接法
- 反证法
审题拆解
(构建基础)
执行阶段
(逻辑链条构建)
已知条件
↓
↓
↓
公理/定义引用
定理/推论衔接推导
过渡结论生成
循环逼近结论
收尾阶段
(闭环验证)
结论匹配
- 覆盖命题
- 边界检验
表述规范
- 符号标准化
复盘校验
- 特例反代
课堂总结
1.反证法本质:
通过“否定结论→推导矛盾→肯定原结论”的间接证明方法
2. 三步骤流程(逻辑闭环)
步骤 关键操作
① 否定结论 假设命题结论不成立
② 推出矛盾 结合已知条件,推导出矛盾
③ 肯定结论 因假设不成立,原命题得证
3. 四大适用场景
1. 否定性命题
2. 唯一性命题
3.“至少/至多”类命题
4. 难以直接构造的命题
感谢聆听!
青岛版2024·八年级上册
1.3 几何证明举例
第一章
推理与证明
1.3.3 反证法的证明范式
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
如何证明
互逆命题的推导与证明
推论的意义与运用
反证法的证明范式
合情推理到逻辑推理
学 习 目 标
1
2
能复述反证法三步骤:① 假设命题不成立 → ② 推导矛盾 → ③ 原命题成立
能辨别反证法使用场景(存在性、唯一性、无限性命题)
3
能用反证法完成经典证明
情境导入
第五公设:一场两千年的几何战争
阿
基
米
德
→
牛顿
全军覆没!
两千年前,欧几里得写下第五公设——主要说明过一点有且只有一条直线与已知直线平行!一时之间,所有数学家都想证明这个又长又怪的公设
俄罗斯‘几何狂人’罗巴切夫斯基: 既然证明不了,不如彻底造反!
假设过一点→两条平行线!
然而若是该假设成立,竟会发现三角形的内角和小于180°
情境导入
反证法:在荒谬中炸出新宇宙
如此荒谬的假设,你会认同吗?
不!他用反证法挖出了新宇宙 罗氏几何! 爱因斯坦用此推翻牛顿引力,重塑时空!
反证法究竟有何等威力 能把把‘不可能’变成新世界的基石?
接下来,让我们走进课堂,了解什么是反证法!如何使用反证法!
新知探究
反证法——当直接证明“走不通”时的思维突围
当一个命题从已知条件出发不易直接证得结论时,还有其他方法吗?
思考与交流
1
2
∠1=∠2
你常用的直接证明方法是什么?
试试用“新方法”证明熟悉的定理
证明平行线的性质定理Ⅰ:
两条平行直线被第三条直线所截,同位角相等
提示:
如果“假设同位角不相等”,会发生什么?
案例解析:用反证法证明平行线同位角相等
新知探究
已知:如图,直线AB∥CD,直线EF与AB、CD分别相交于点G、H。
求证:∠1=∠2。
【证明】
假设:∠1≠∠2(提出反面假设)
过点G作直线A'B',使∠EGB'=∠2
所以A'B'∥CD(同位角相等,两直线平行)
因为AB∥CD(已知)
所以过点G有两条直线AB、A'B'均平行于CD
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾
所以∠1≠∠2的假设不成立
所以∠1=∠2
A
C
B
D
E
F
G
H
A`
B`
1
2
方法技巧
反证法与直接证明的“区别”:
直接证明:从已知条件出发,正向推导到结论
反证法:从结论的反面出发,逆向推导到矛盾,从而间接证明结论
知识小结
反证法:从“假设反面”到“证明结论”的逻辑闭环
以上这种证明方法有怎样的特点?它包括了哪几个步骤?
反证法的核心特点
- **间接性**:不直接证明结论,而是通过“否定反面”间接验证;
概括与表达
- **矛盾性**:核心是“推导矛盾”(与已知条件、定理冲突)
- **逻辑性**:严格遵循“假设→推导→结论”的闭环,无逻辑漏洞。
反证法的三步流程
① **否定结论**
假设命题的结论不成立
② **推出矛盾**
从假设出发,结合已知条件,推导出自相矛盾的结果
③ **肯定结论**
由矛盾判定假设不成立,从而证明原结论
**反证法**:提出与命题的结论相反的假设,再从假设出发推出矛盾,从而证明命题成立的方法
新知探究
情境一:“以有证无”,反证法破解否定性命题的核心逻辑
1.用反证法证明: 一个三角形中不可能有两个直角
假设△ABC中有两个直角,不妨设∠A=∠B=90°
因为∠A+∠B+∠C=180°(三角形内角和定理)
所以90°+90°+∠C=180°(等量代换)
所以∠C=0°(等式的性质)
但∠C=0°与三角形内角的定义矛盾(三角形的每个内角都大于0°)
因此,“△ABC中有两个直角”的假设不成立
【证明】
原命题得证: 一个三角形中不可能有两个直角
方法技巧
直接证明“不存在”“没有”“不可能”非常困难(无法穷举所有情况),但假设“存在”“有”,更容易导出矛盾。
新知探究
情景二:反证法破“至少/至多”题:从“全反假设”到“矛盾突破”
2.用反证法证明:在直角三角形中,至少有一个锐角不大于45°
已知:设直角三角形ABC中,∠C=90°
求证:∠A或∠B中至少有一个≤45°
【证明】假设∠A>45°,∠B>45°
因为∠A+∠B+∠C=180°(三角形的内角和定理)
且∠C=90°(已知)
所以∠A+∠B=90°(等量代换,等式的性质)
因为∠A>45°且∠B>45°(已知)
所以∠A+∠B>45°+45°=90°
这与∠A+∠B=90°矛盾
所以假设不成立,原命题得证
方法技巧
(1)“至少一个”的反面是“全不”(如“至少有一个锐角≤45°”的反面是“所有锐角都>45°”);
(2)“至多一个”的反面是“至少两个”(如“至多有一个直角”的反面是“有两个或更多直角”)
新知探究
情景三:反证法破“唯一性”命题,用“多”的假设,证“一”的必然
3.平行公理——过直线外一点只有一条直线与已知直线平行
已知:直线l,点P在l外;
求证:过P只有一条直线与l平行
证明:假设过P有两条直线 、都平行于l( )
因为 //l, //l,且 (已知)
所以 (平行线的传递性)
因为 、都过点P(已知)
所以 ,即二者重合(两点确定一条直线的基本事实)
这与假设矛盾,假设不成立,原命题得证。
P
l
方法技巧
直接证明“只有一个”需要排除所有其他可能,而假设“有两个或更多”,更容易通过逻辑推导矛盾(如与定义、定理冲突)。
知识小结
反证法的适用情境归纳
核心逻辑
反证法的本质是 “否定反面→推导矛盾→肯定原结论”,适用于直接证明困难的命题
四大适用情境
1. 否定性命题
特点:证明“不存在”“不可能”“没有”
2. 唯一性命题
特点:证明“唯一”“只有一个”“有且仅有”
3. “至少/至多”类命题
特点:证明“至少有一个”“至多有一个”
4. 难以直接构造的命题
特点:无法通过直接举例或正向推导证明
证明的方法主要有两种:直接证明与间接证明,而“反证法”就是间接证明的典型方法
课堂练习
1.下列关于反证法证明平行公理的步骤, 顺序正确 的是( )
① 两条直线都过P且平行,必重合;
② 假设过P有两条不同直线与l平行;
③ 假设不成立,原命题得证;
④ 由平行传递性得两条直线平行。
A. ②→④→①→③
B. ①→②→③→④
C. ③→②→①→④
D. ②→①→④→③
导出矛盾
假设反面
得出结论
推导过程
答案解析:假设推导矛盾是反证法解答的一般过程,故选A
方法技巧
反证法的核心流程是“假设→推导→矛盾→结论”
课堂练习
2. 用反证法证明“三角形中不可能有两个钝角”时, 推导过程中导出的矛盾 是( )
A.与“三角形内角和为180°”矛盾
B. 与“钝角的定义(大于90°)”矛盾
C. 与“平行线性质”矛盾
D. 与“线段中点的定义”矛盾
否定性命题
【解】
否定性命题,该将“不可能”假设为“必然”
假设三角形中有两个钝角(设为∠A>90°,∠B>90°),则∠A+∠B>180°
加上第三个角∠C>0°,三角形内角和∠A+∠B+∠C>180°
与“三角形内角和为180°”的定理矛盾,故选择A。
方法技巧
解题关键:
能够对要进行的命题进行假设,根据假设的内容推导出与之相对应的矛盾
课堂练习
3.下列命题中,最适合用反证法证明的是:( )
三角形的内角和为180° B. 是无理数
C. 二次函数的图像是抛物线 D. 直角三角形的勾股定理
性质定理
无法正向推导的命题
性质定理
性质定理
【解】
在以上四个选项中,性质定理都可以通过正向推理得出,但“ 是无理数 ”是难以正向推导的命题,故选B
方法技巧
解答关键:
能清楚的了解“反证法使用的四大场景”
1.否定性命题
2.唯一性命题
3.“至多/至少”类命题
4.无法正向推导的命题
课堂练习
用反证法证明:三角形的三个内角中,至少有一个内角大于或等于60°
已知:△ABC是任意三角形;
求证:∠A,∠B,∠C中至少有一个≥60°
证明:假设△ABC的三个内角都小于60°,即∠A<60°,∠B<60°,∠C<60°
因为∠A+∠B+∠C<60°+60°+60°=180°(三角形内角和定理)
所以∠A+∠B+∠C<180°与三角形内角和定理(∠A+∠B+∠C=180°)矛盾
所以,“三个内角都小于60°”的假设不成立,原结论得证
本题核心逻辑:
假设反面(都<60°)→推导(和<180°)
→矛盾(与内角和定理冲突)
→肯定原结论(至少一个≥60°)
方法技巧
课堂练习
用反证法证明:
已知:a+b>0
求证:a,b中至少有一个大于零。
假设a,b都不大于零,即a≤0且b≤0
所以a+b≤0+0=0(不等式加法性质)
因为a+b≤0与已知条件a+b>0矛盾
所以“a,b都不大于零”的假设不成立
原结论得证: a。b中至少有一个大于零
证明:
经过以上的练习,你对推理与证明的过程与方法是否完全熟悉了?
现在我们已经掌握了证明题的证明步骤,也对证明的方法和过程进行了深入的学习,那么证明题的完整逻辑流程是什么呢?
知识小结
证明题的逻辑流程
准备阶段
- 核心命题
- 隐含条件
策略选择
- 直接法
- 反证法
审题拆解
(构建基础)
执行阶段
(逻辑链条构建)
已知条件
↓
↓
↓
公理/定义引用
定理/推论衔接推导
过渡结论生成
循环逼近结论
收尾阶段
(闭环验证)
结论匹配
- 覆盖命题
- 边界检验
表述规范
- 符号标准化
复盘校验
- 特例反代
课堂总结
1.反证法本质:
通过“否定结论→推导矛盾→肯定原结论”的间接证明方法
2. 三步骤流程(逻辑闭环)
步骤 关键操作
① 否定结论 假设命题结论不成立
② 推出矛盾 结合已知条件,推导出矛盾
③ 肯定结论 因假设不成立,原命题得证
3. 四大适用场景
1. 否定性命题
2. 唯一性命题
3.“至少/至多”类命题
4. 难以直接构造的命题
感谢聆听!
同课章节目录
