1.2证明(第1课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册
文档属性
| 名称 | 1.2证明(第1课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 07:56:50 | ||
图片预览





文档简介
(共20张PPT)
青岛版2024·八年级上册
1.2. 证明
第一课时
从合情推理到逻辑推理
第一章
推理与证明
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
合情推理到逻辑推理
如何证明
代数推理
几何证明
学 习 目 标
1
2
通过实验反例质疑观察、归纳等合情推理的可靠性,理解逻辑推理的必要性;
掌握推理的基本依据(定义、基本事实、运算法则),能进行简单代数推理。
情境导入
不可能的图形——彭罗斯三角
在图片中,你所看到的是一个完整的封闭图形
当你看到这个图形之后,你是否会怀疑其存在的合理性?
我们不妨换个角度来看看该图形
我们通过眼睛观察,就定义了它是一个完整的封闭图形,但事实却并非如此
情境导入
以上的情境中,我们仅仅通过观察得出了该图形是封闭,但事实上视觉却欺骗了我们,但在数学中,这样的方法却常常在使用。
观察、
实验、
类比、
归纳,
是我们发现规律,获取一般结论的重要方法。
但是这些方法一定正确吗?
新知探究
1.观察该图中的两条黑色直线,它们是直线吗?
2.用度量或拼剪的方法发现一个或几个三角形的内角和都是180°,由此猜想任意一个三角形的内角和都是180°。这种通过实验获得的结论一定正确吗?
两个正数的和大于每一个加数
两个正数的和大于每一个加数
类比
3.由类比得到的结论正确吗?
归纳
新知探究
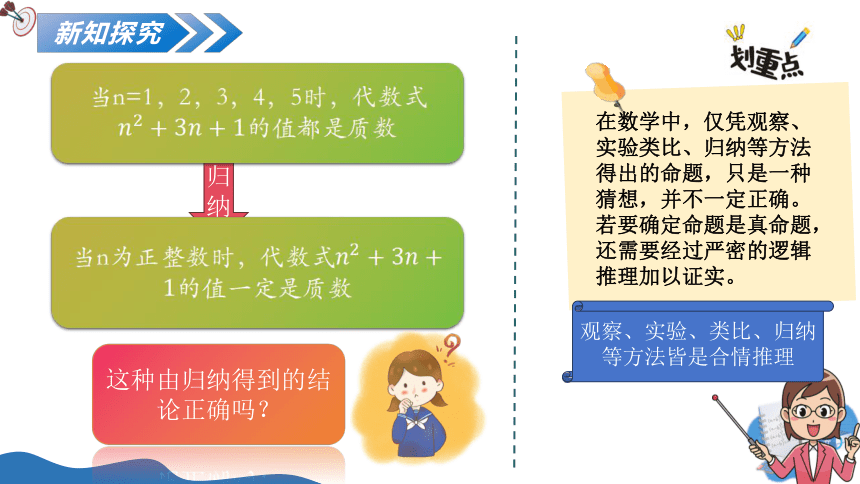
当n=1,2,3,4,5时,代数式的值都是质数
当n为正整数时,代数式的值一定是质数
这种由归纳得到的结论正确吗?
在数学中,仅凭观察、实验类比、归纳等方法得出的命题,只是一种猜想,并不一定正确。若要确定命题是真命题,还需要经过严密的逻辑推理加以证实。
观察、实验、类比、归纳等方法皆是合情推理
.
既然合情推理不一定能得到准确的结论,那该依据什么来进行严密的逻辑推理呢?我们一起来看看下面这个例子。
如果a=b,b=c,那么a=c
如果a>b,b=c,那么a>c
仔细观察你会发现,在这两个命题的推理中,都用到如下规律:
一个量可以用的等量来替换,也就是
等量代换
像等量代换这样公认的真命题,即为
基本事实
提分笔记
在代数推理中,可以依据定义、运算法则、运算律、公式、等式(不等式)的基本性质进行运算和推理
即时训练
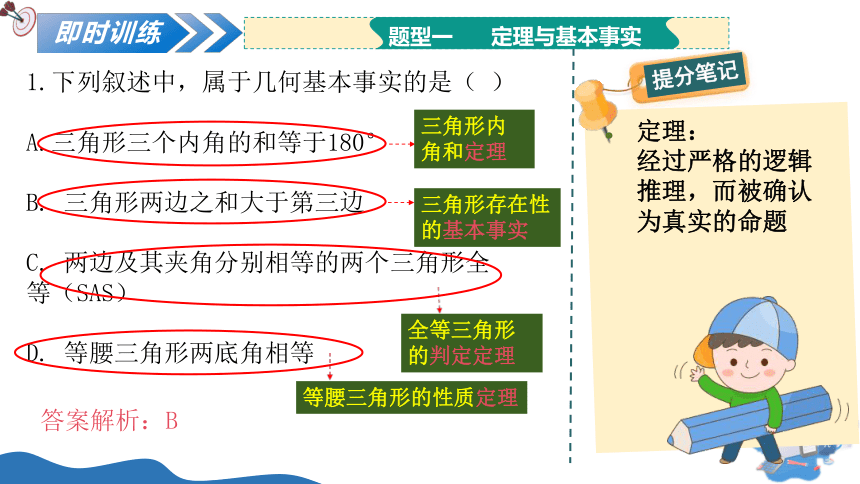
1.下列叙述中,属于几何基本事实的是( )
A.三角形三个内角的和等于180°
B. 三角形两边之和大于第三边
C. 两边及其夹角分别相等的两个三角形全等(SAS)
D. 等腰三角形两底角相等
三角形内角和定理
三角形存在性的基本事实
全等三角形的判定定理
等腰三角形的性质定理
答案解析:B
提分笔记
定理:
经过严格的逻辑推理,而被确认为真实的命题
定理与基本事实
题型一
即时训练
2.下列命题中,可直接作为推理依据的基本事实是( )。
A.两直线平行,同位角相等
B. 两点之间,线段最短
C. 三角形的外角等于与它不相邻的两个内角的和
D. 直角三角形的两个锐角互余
三角形内角和定理
几何基本事实
三角形外角定理
直角三角形的性质定理
方法技巧
能够区分定理与基本事实,是解决该类题目的关键,定理一般都是可证明的
定理与基本事实
题型一
等式的基本性质(其一)
等式的两边同时加上或减去同一个整式,结果仍是等式
例题讲解
【例】说明下列命题是真命题:
(1)如果ab=a(a是有理数,且a),那么b=1;
等式
结果
【解】因为ab=a(a是有理数,且a)
(已知)
所以
(等式的基本性质)
所以
(除法的运算结果)
提分笔记
例题讲解
(2)如果a,b都是奇数,那么a+b是是偶数。
【解】因为a,b都是奇数
(已知)
设a=2m+1,b=2n+1,其中m,n都是整数
(奇数的定义)
所以a+b=2m+1+2n+1=2(m+n+1)
(乘法分配律)
因为m,n是整数
(已知)
所以m+n+1是整数
(整数的基本性质)
所以2(m+n+1)是偶数
(偶数的定义)
所以a+b是偶数
(等量代换)
学习提示
在学习推理的初始阶段,要在推理过程每一步的后面,用括号注明推理的依据
即时训练
1. 通过画图,小亮发现三角形的三条中线都在三角形的内部,三角形的三条角平分线也都在三角形的内部,于是推断三角形的三条高都在三角形的内部。小亮的结论正确吗?为什么?
【解】小亮的结论 不正确。
因为三角形的高是“从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段”
(三角形高的定义)
而钝角三角形中,两个锐角所对边上的高需延长对边才能作垂线,这两条高在三角形外部
(三角形高的位置特征)
所以“三角形的三条高都在内部”仅对锐角三角形成立,小亮结论错误
(反例法:钝角三角形存在高在外部)
解题的关键:清楚的知道三角形的高的概念,并会画不同三角形的高,同时对三角形的分类由清晰的认识
逻辑推理的具体过程
题型二
即时训练
2. 说明下列命题是真命题:
(1)如果 a + b = 0,那么 a = -b;
(2)如果 a 是奇数,b 是偶数,那么 a + b 是奇数;
(3)三个连续整数的和是3的倍数。
解(1)因为 a + b = 0
(已知)
所以 (a + b) - b = 0 - b
(等式的基本性质)
即 a + b - b = -b
(去括号法则)
所以 a = -b
(合并同类项法则)
提分笔记
去括号法则:
若括号前是“+”号,去掉括号后括号内的每一项不变号;
若括号前是“-”号,去掉括号后括号内的每一项变为原来的相反数
即时训练
(2)解:因为 a 是奇数, b 是偶数
(已知)
所以设 a = 2m + 1,设 b = 2n(m,n是整数)
(奇数与偶数的定义)
所以 a + b = (2m + 1) + 2n
(等量代换)
整理得 a + b = 2m + 2n + 1 = 2(m + n) + 1
(加法结合律、乘法分配律)
因为 m, n 是整数
(已知)
所以 m + n 是整数
(整数的基本性质)
令 k = m + n(k是整数),则 a + b = 2k + 1
(等量代换)
所以 a + b 是奇数
(奇数的定义)
根据奇数与偶数的定义:
我们常将奇数表示为2n+1,
将偶数表现为2n,
其中n为整数
(3)解:设三个连续整数分别为 n,n + 1,n + 2(n 是整数)
(相邻整数相差1)
它们的和为 n + (n + 1) + (n + 2)
(已知)
整理的3n + 3
(去括号与合并同类项法则)
因为 n 是整数,所以 n + 1 是整数
(整数的基本性质)
因为 3n+3=3(n+1)
(乘法分配律)
所以3(n+1)是整数
(3的倍数的定义)
所以3个连续的整数的和是3的倍数
(等量代换)
熟悉已经学过的定义、运算法则、运算律以及各类公式在进行代数推理时才能做到逻辑缜密,过程严谨
课堂练习
1.说明下列命题是真命题;
(1)如果b=2a (2)如果ab=1,那么b=
【解】(1)因为
所以
(分式有意义的条件)
左右两边同时乘a得
(等式的基本性质)
所以b=2a
(等式变形的结果)
(已知)
(2)因为ab=1
(已知)
假设a=0,则ab=0但ab=1,所以a
(反证法)
左右两边同时除a得ab
(等式的基本性质)
所以b=
所以该命题是真命题
所以该命题是真命题
(等式变形的结果)
课堂练习
证明:因为∠ABE与∠DBC互为余角( ),
所以∠ABE + ∠DBC = 90°( )。
因为点B在直线AC上( ),
所以∠ABE + ∠EBD + ∠DBC = 180°( )。
所以90°+ ∠EBD = 180°( )。
所以∠EBD = 90°( )。
所以BE ⊥BD ( )。
已知
余角的定义
已知
平角的定义
等量代换
等式的基本性质
垂直的定义
2. 阅读证明过程,并在括号内填写推理依据。
如图,点B在直线AC上,∠ABE与∠DBC互为余角。求证:BE ⊥BD。
课堂总结
合情推理
逻辑推理
观察
实验
类比
归纳
在信息不完全或不确定的情况下做出最佳判断或预测
依据
定义
基本事实
依据定义或基本事实进行严格推导
感谢聆听!
青岛版2024·八年级上册
1.2. 证明
第一课时
从合情推理到逻辑推理
第一章
推理与证明
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
合情推理到逻辑推理
如何证明
代数推理
几何证明
学 习 目 标
1
2
通过实验反例质疑观察、归纳等合情推理的可靠性,理解逻辑推理的必要性;
掌握推理的基本依据(定义、基本事实、运算法则),能进行简单代数推理。
情境导入
不可能的图形——彭罗斯三角
在图片中,你所看到的是一个完整的封闭图形
当你看到这个图形之后,你是否会怀疑其存在的合理性?
我们不妨换个角度来看看该图形
我们通过眼睛观察,就定义了它是一个完整的封闭图形,但事实却并非如此
情境导入
以上的情境中,我们仅仅通过观察得出了该图形是封闭,但事实上视觉却欺骗了我们,但在数学中,这样的方法却常常在使用。
观察、
实验、
类比、
归纳,
是我们发现规律,获取一般结论的重要方法。
但是这些方法一定正确吗?
新知探究
1.观察该图中的两条黑色直线,它们是直线吗?
2.用度量或拼剪的方法发现一个或几个三角形的内角和都是180°,由此猜想任意一个三角形的内角和都是180°。这种通过实验获得的结论一定正确吗?
两个正数的和大于每一个加数
两个正数的和大于每一个加数
类比
3.由类比得到的结论正确吗?
归纳
新知探究
当n=1,2,3,4,5时,代数式的值都是质数
当n为正整数时,代数式的值一定是质数
这种由归纳得到的结论正确吗?
在数学中,仅凭观察、实验类比、归纳等方法得出的命题,只是一种猜想,并不一定正确。若要确定命题是真命题,还需要经过严密的逻辑推理加以证实。
观察、实验、类比、归纳等方法皆是合情推理
.
既然合情推理不一定能得到准确的结论,那该依据什么来进行严密的逻辑推理呢?我们一起来看看下面这个例子。
如果a=b,b=c,那么a=c
如果a>b,b=c,那么a>c
仔细观察你会发现,在这两个命题的推理中,都用到如下规律:
一个量可以用的等量来替换,也就是
等量代换
像等量代换这样公认的真命题,即为
基本事实
提分笔记
在代数推理中,可以依据定义、运算法则、运算律、公式、等式(不等式)的基本性质进行运算和推理
即时训练
1.下列叙述中,属于几何基本事实的是( )
A.三角形三个内角的和等于180°
B. 三角形两边之和大于第三边
C. 两边及其夹角分别相等的两个三角形全等(SAS)
D. 等腰三角形两底角相等
三角形内角和定理
三角形存在性的基本事实
全等三角形的判定定理
等腰三角形的性质定理
答案解析:B
提分笔记
定理:
经过严格的逻辑推理,而被确认为真实的命题
定理与基本事实
题型一
即时训练
2.下列命题中,可直接作为推理依据的基本事实是( )。
A.两直线平行,同位角相等
B. 两点之间,线段最短
C. 三角形的外角等于与它不相邻的两个内角的和
D. 直角三角形的两个锐角互余
三角形内角和定理
几何基本事实
三角形外角定理
直角三角形的性质定理
方法技巧
能够区分定理与基本事实,是解决该类题目的关键,定理一般都是可证明的
定理与基本事实
题型一
等式的基本性质(其一)
等式的两边同时加上或减去同一个整式,结果仍是等式
例题讲解
【例】说明下列命题是真命题:
(1)如果ab=a(a是有理数,且a),那么b=1;
等式
结果
【解】因为ab=a(a是有理数,且a)
(已知)
所以
(等式的基本性质)
所以
(除法的运算结果)
提分笔记
例题讲解
(2)如果a,b都是奇数,那么a+b是是偶数。
【解】因为a,b都是奇数
(已知)
设a=2m+1,b=2n+1,其中m,n都是整数
(奇数的定义)
所以a+b=2m+1+2n+1=2(m+n+1)
(乘法分配律)
因为m,n是整数
(已知)
所以m+n+1是整数
(整数的基本性质)
所以2(m+n+1)是偶数
(偶数的定义)
所以a+b是偶数
(等量代换)
学习提示
在学习推理的初始阶段,要在推理过程每一步的后面,用括号注明推理的依据
即时训练
1. 通过画图,小亮发现三角形的三条中线都在三角形的内部,三角形的三条角平分线也都在三角形的内部,于是推断三角形的三条高都在三角形的内部。小亮的结论正确吗?为什么?
【解】小亮的结论 不正确。
因为三角形的高是“从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段”
(三角形高的定义)
而钝角三角形中,两个锐角所对边上的高需延长对边才能作垂线,这两条高在三角形外部
(三角形高的位置特征)
所以“三角形的三条高都在内部”仅对锐角三角形成立,小亮结论错误
(反例法:钝角三角形存在高在外部)
解题的关键:清楚的知道三角形的高的概念,并会画不同三角形的高,同时对三角形的分类由清晰的认识
逻辑推理的具体过程
题型二
即时训练
2. 说明下列命题是真命题:
(1)如果 a + b = 0,那么 a = -b;
(2)如果 a 是奇数,b 是偶数,那么 a + b 是奇数;
(3)三个连续整数的和是3的倍数。
解(1)因为 a + b = 0
(已知)
所以 (a + b) - b = 0 - b
(等式的基本性质)
即 a + b - b = -b
(去括号法则)
所以 a = -b
(合并同类项法则)
提分笔记
去括号法则:
若括号前是“+”号,去掉括号后括号内的每一项不变号;
若括号前是“-”号,去掉括号后括号内的每一项变为原来的相反数
即时训练
(2)解:因为 a 是奇数, b 是偶数
(已知)
所以设 a = 2m + 1,设 b = 2n(m,n是整数)
(奇数与偶数的定义)
所以 a + b = (2m + 1) + 2n
(等量代换)
整理得 a + b = 2m + 2n + 1 = 2(m + n) + 1
(加法结合律、乘法分配律)
因为 m, n 是整数
(已知)
所以 m + n 是整数
(整数的基本性质)
令 k = m + n(k是整数),则 a + b = 2k + 1
(等量代换)
所以 a + b 是奇数
(奇数的定义)
根据奇数与偶数的定义:
我们常将奇数表示为2n+1,
将偶数表现为2n,
其中n为整数
(3)解:设三个连续整数分别为 n,n + 1,n + 2(n 是整数)
(相邻整数相差1)
它们的和为 n + (n + 1) + (n + 2)
(已知)
整理的3n + 3
(去括号与合并同类项法则)
因为 n 是整数,所以 n + 1 是整数
(整数的基本性质)
因为 3n+3=3(n+1)
(乘法分配律)
所以3(n+1)是整数
(3的倍数的定义)
所以3个连续的整数的和是3的倍数
(等量代换)
熟悉已经学过的定义、运算法则、运算律以及各类公式在进行代数推理时才能做到逻辑缜密,过程严谨
课堂练习
1.说明下列命题是真命题;
(1)如果b=2a (2)如果ab=1,那么b=
【解】(1)因为
所以
(分式有意义的条件)
左右两边同时乘a得
(等式的基本性质)
所以b=2a
(等式变形的结果)
(已知)
(2)因为ab=1
(已知)
假设a=0,则ab=0但ab=1,所以a
(反证法)
左右两边同时除a得ab
(等式的基本性质)
所以b=
所以该命题是真命题
所以该命题是真命题
(等式变形的结果)
课堂练习
证明:因为∠ABE与∠DBC互为余角( ),
所以∠ABE + ∠DBC = 90°( )。
因为点B在直线AC上( ),
所以∠ABE + ∠EBD + ∠DBC = 180°( )。
所以90°+ ∠EBD = 180°( )。
所以∠EBD = 90°( )。
所以BE ⊥BD ( )。
已知
余角的定义
已知
平角的定义
等量代换
等式的基本性质
垂直的定义
2. 阅读证明过程,并在括号内填写推理依据。
如图,点B在直线AC上,∠ABE与∠DBC互为余角。求证:BE ⊥BD。
课堂总结
合情推理
逻辑推理
观察
实验
类比
归纳
在信息不完全或不确定的情况下做出最佳判断或预测
依据
定义
基本事实
依据定义或基本事实进行严格推导
感谢聆听!
同课章节目录
