1.2证明(第2课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册
文档属性
| 名称 | 1.2证明(第2课时)课件(共20张PPT) 2025-2026学年青岛版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 07:58:34 | ||
图片预览



文档简介
(共20张PPT)
青岛版2024·八年级上册
1.2. 证明
第二课时
如何证明
第一章
推理与证明
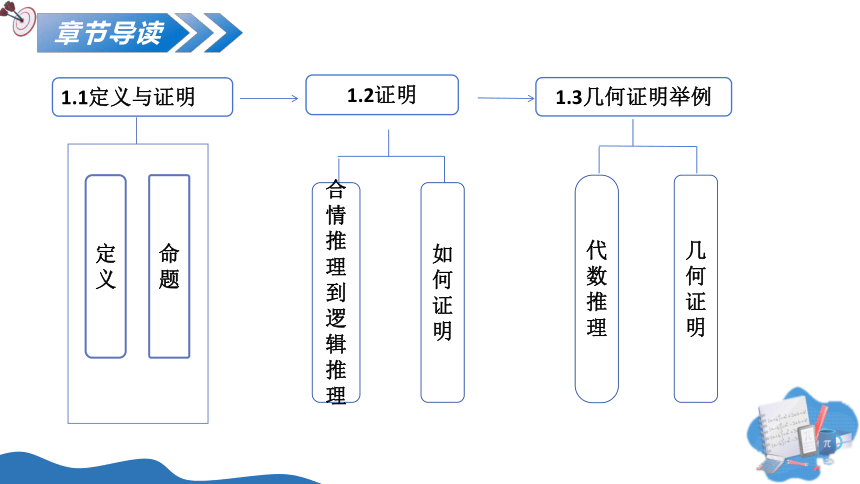
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
合情推理到逻辑推理
如何证明
代数推理
几何证明
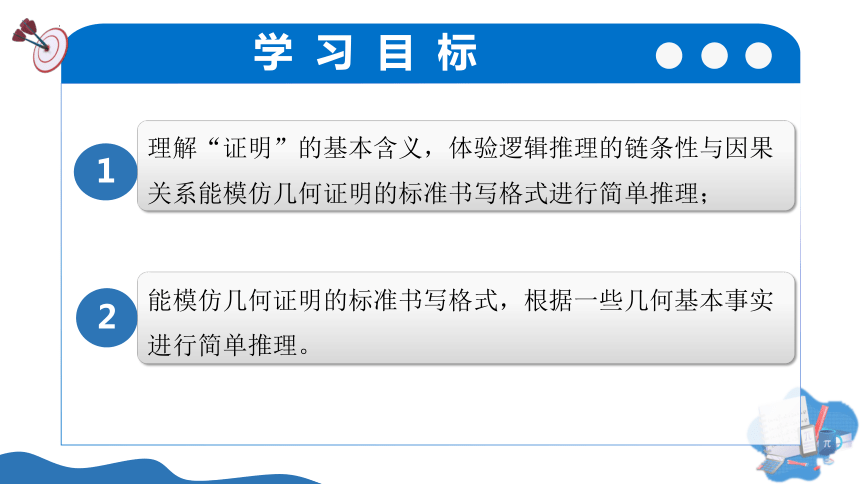
学 习 目 标
1
2
理解“证明”的基本含义,体验逻辑推理的链条性与因果关系能模仿几何证明的标准书写格式进行简单推理;
能模仿几何证明的标准书写格式,根据一些几何基本事实进行简单推理。
情境导入
故事启航——遇见《几何原本》
万历年间,几个金发碧眼的意大利人抵达北京。其中利玛窦神甫的行李里,藏着一本欧几里得的《几何原本》。
当他把“三角形内角和等于两个直角”的定理展示给翰林院学士时,满堂哗然!
但年轻的徐光启却被迷住了,它发现其中证明,环环相扣,如锁链难摧。
他执意与利玛窦合译此书, 并定名为《几何原本》
而这场几何之风,悄然吹动了东方思维之锚。
情境导入
故事启航——遇见《几何原本》
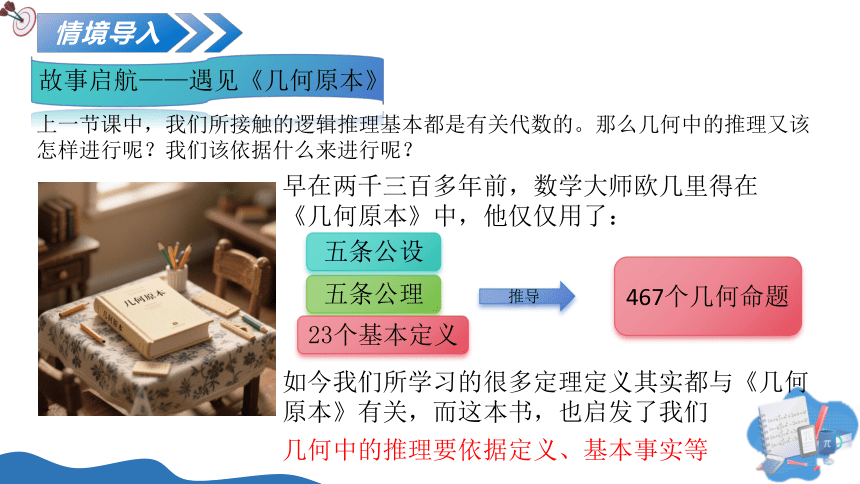
上一节课中,我们所接触的逻辑推理基本都是有关代数的。那么几何中的推理又该怎样进行呢?我们该依据什么来进行呢?
五条公理
五条公设
23个基本定义
推导
467个几何命题
早在两千三百多年前,数学大师欧几里得在《几何原本》中,他仅仅用了:
如今我们所学习的很多定理定义其实都与《几何原本》有关,而这本书,也启发了我们
几何中的推理要依据定义、基本事实等
新知探究
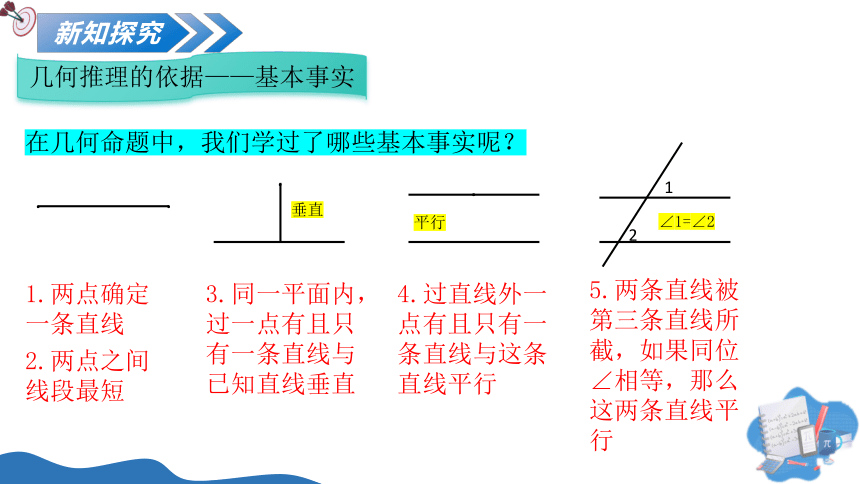
几何推理的依据——基本事实
.
.
1.两点确定一条直线
2.两点之间线段最短
在几何命题中,我们学过了哪些基本事实呢?
.
垂直
3.同一平面内,过一点有且只有一条直线与已知直线垂直
.
平行
4.过直线外一点有且只有一条直线与这条直线平行
1
2
∠1=∠2
5.两条直线被第三条直线所截,如果同位∠相等,那么这两条直线平行
新知探究
逻辑推理的过程——证明
以上五条基本事实,就像数学大厦的基石一样,是无需加以论证的“起点”命题,虽然简单,却是接下来进行复杂推理的坚实依据。
但当我们遇见新的、不显而易见的数学问题时,该怎么办呢?
这时候就需要证明,什么是证明呢?
定义、基本事实为依据
逻辑推理
新结论、命题
证明
新知探究
开启证明之旅:几何推理的探索与实践
以上我们知道了何为证明,那么如何证明?我们以证明“对顶角相等”为例。
分析:首先我们要先明确该命题的条件和结论。
条件:如果两个角是对顶角
结论:那么这两个角相等
同时为了推理过程更加精确、简约,便于论证,
文字语言的条件和结论
图形语言和符号语言
如图,如果AB, CD交于点O,∠AOC与∠BOD是对顶∠,那么∠AOC=∠BOD
该命题是否正确呢?
新知探究
开启证明之旅:几何推理的探索与实践
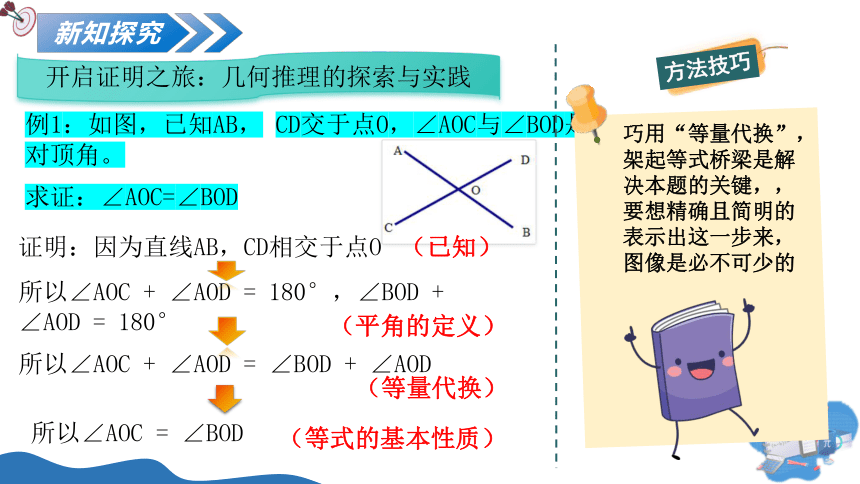
例1:如图,已知AB, CD交于点O,∠AOC与∠BOD是对顶角。
求证:∠AOC=∠BOD
证明:因为直线AB,CD相交于点O
(已知)
所以∠AOC + ∠AOD = 180°,∠BOD + ∠AOD = 180°
(平角的定义)
所以∠AOC + ∠AOD = ∠BOD + ∠AOD
(等量代换)
所以∠AOC = ∠BOD
(等式的基本性质)
巧用“等量代换”,架起等式桥梁是解决本题的关键,,要想精确且简明的表示出这一步来,图像是必不可少的
方法技巧
新知探究
1.定理的定义与属性
开启证明之旅:几何推理的探索与实践
2.几何证明步骤(概括与表达)
定义
我们把推理证实过的真命题叫做定理
例如
对顶角相等
属性
定理和基本事实一样,也可以作为证明的依据
一
二
三
根据题意,画出图形
结合图形,写出“已知”“求证”
写出“证明”
根据以上的证明过程,我们可以得出以下结论:
下面我们试试将刚刚总结的步骤运用于实际证明中
新知探究
证明:等角的余角相等
已知: ∠α = ∠β,∠1 是∠α 的余角,∠2 是∠β 的余角。
求证:∠1 = ∠2。
证明:因为∠1 是∠α 的余角,∠2 是∠β 的余角
(已知)
所以∠1 + ∠α = 90°,∠2 + ∠β = 90°
(余角的定义)
所以∠1 + ∠α = ∠2 + ∠β
(等量代换)
因为∠α = ∠β
(已知)
所以∠1 = ∠2
(等式的基本性质)
方法技巧
解决本题的核心是用“余角定义”搭建数量关系,用“等量代换+等式性质”完成逻辑推导
即时训练
1.阅读证明过程,并在括号内填写推理依据。
如图,B,C 是线段 AD 上的两点,且 AB = CD。求证:AC = BD。
证明:因为 AB = CD
所以 AB + BC = CD + BC
所以 AC = BD
已知
等式的基本性质
线段的和的定义
提分笔记
这道题渗透了“从已知条件出发,结合基本性质与图形定义推导结论”的几何证明思维,,这种“条件→性质→结论”的逻辑链会反复用到
( )
( )
( )
即时训练
2.如图,∠ABC = ∠A'B'C',BD 和 B'D' 分别是∠ABC 和∠A'B'C'的平分线。
求证:∠ABD = ∠A'B'D'。
证明:因为 BD 是∠ABC 的平分线
(已知)
所以∠ABD =∠ABC
(角平分线的定义)
同理,B'D' 是∠A'B'C' 的平分线
(已知)
所以∠A'B'D' = ∠A'B'C'
(角平分线的定义)
又因为∠ABC = ∠A'B'C'
(已知)
所以 ∠ABC = ∠A'B'C'
(等式的基本性质)
所以∠ABD = ∠A'B'D'
(等量代换)
“等量代换”是几何证明的“桥梁工具”,当直接证两个量相等困难时,找“中间共同量”串联逻辑。
课堂小结
几何证明的三步法:思维转化的完整链条
画图
写已知求证
证明
以上证明过程并非机械流程,而是体现
直观
抽象
逻辑
特别是在证明这一步时,一般使用的演绎推理(如三段论)串联论据,构建“前提”的逻辑链
如在“等角的余角相等”的证明中,就用了使用了这样的逻辑链
余角定义
等量代换
等式的性质
课堂练习
能力提升
1.如图,直线AB,CD相交于点O,其中∠AOC是直角。
求证:∠BOC,∠BOD,∠AOD都是直角。
证明:因为AB是一条直线
(已知)
所以∠BOC = 180° - ∠AOC = 180° - 90° = 90°
(等式的性质)
所以∠BOC是直角
所以∠AOC + ∠BOC = 180°
(邻补角性质)
(直角定义)
因为∠BOD与∠AOC是对顶角
(对顶角的定义)
所以∠BOD=∠AOC=90°
(对顶角的性质)
同理∠AOD是直角
所以∠BOD是直角
(直角定义)
(对顶角的定义与性质)
在数学证明中,“同理” 是一种常用的表达方式,但它是一把双刃剑——用得恰当可以精简证明,避免重复用得不恰当则会导致逻辑漏洞、表述不清,甚至完全错误;
课堂练习
2.参考等角的余角相等的过程,证明:等角的补角相等
已知: ∠α = ∠β,∠1 是∠α 的补角,∠2 是∠β 的补角。
求证:∠1 = ∠2。
证明:因为∠1 是∠α 的补角,∠2 是∠β 的补角
(已知)
所以∠1 + ∠α = 180°,∠2 + ∠β = 180°
(补角的定义)
所以∠1 + ∠α = ∠2 + ∠β
(等量代换)
因为∠α = ∠β
(已知)
所以∠1 = ∠2
(等式的基本性质)
条件:如果两个角相等 结论:那么它们的补角相等
方法技巧
类比“等角的余角相等”这一命题的证明,发现两个题都用到了等量代换,和等式的性质
能力提升
课堂练习
3.说明“如果一个三位数的三个数位上的数字的和能被3整除,那么这个三位数能被3整除”是真命题
证明:设该三位数的百位数字为 ,十位数字为 ,个位数字为 =3k(k为整数,a,b,c均为0-9的整数)
这个三位数可以表示为
(已知)
(三位数的数值展开式)
(加法结合律)
因为9和99是3的倍数
(3的倍数的定义)
所以99a+9b=3(33a+3b),其中(33a+3b)是整数
(整数的定义)
=3[(33a+3b)+k]
(乘法分配律)
所以这三位数能被3整除
解题的关键:
拆分法:将一个数拆分为两个或多个数的和,如 100a=99a+a
10b=9b+b
拓展延伸
课堂练习
变式训练
4.,OC是∠AOB内部可绕点转动的射线,平分,平分。
求证
因为 平分 ,OE 平分 (已知)
所以 ,(角平分线的定义)
因为(角的和的定义)
所以(等量代换)
=(∠AOC+∠BOC)(乘法分配律)
=∠AOB(等量代换)
=α(等量代换)
角平分线的“双向性”:
角平分线既是“拆分工具”(将大角拆为两个相等的小角),也是“合成工具”(两个相等小角的和等于大角)。证明中常作为“等量代换”的依据。
课堂总结
1.什么是证明?
以定义、基本事实为依据,通过逻辑推理的方式得到新命题与结论的过程,叫做证明
2.几何证明步骤
根据题意,画出图形
结合图形,写出“已知”“求证”
写出“证明”
感谢聆听!
青岛版2024·八年级上册
1.2. 证明
第二课时
如何证明
第一章
推理与证明
章节导读
1.1定义与证明
1.2证明
1.3几何证明举例
定义
命题
合情推理到逻辑推理
如何证明
代数推理
几何证明
学 习 目 标
1
2
理解“证明”的基本含义,体验逻辑推理的链条性与因果关系能模仿几何证明的标准书写格式进行简单推理;
能模仿几何证明的标准书写格式,根据一些几何基本事实进行简单推理。
情境导入
故事启航——遇见《几何原本》
万历年间,几个金发碧眼的意大利人抵达北京。其中利玛窦神甫的行李里,藏着一本欧几里得的《几何原本》。
当他把“三角形内角和等于两个直角”的定理展示给翰林院学士时,满堂哗然!
但年轻的徐光启却被迷住了,它发现其中证明,环环相扣,如锁链难摧。
他执意与利玛窦合译此书, 并定名为《几何原本》
而这场几何之风,悄然吹动了东方思维之锚。
情境导入
故事启航——遇见《几何原本》
上一节课中,我们所接触的逻辑推理基本都是有关代数的。那么几何中的推理又该怎样进行呢?我们该依据什么来进行呢?
五条公理
五条公设
23个基本定义
推导
467个几何命题
早在两千三百多年前,数学大师欧几里得在《几何原本》中,他仅仅用了:
如今我们所学习的很多定理定义其实都与《几何原本》有关,而这本书,也启发了我们
几何中的推理要依据定义、基本事实等
新知探究
几何推理的依据——基本事实
.
.
1.两点确定一条直线
2.两点之间线段最短
在几何命题中,我们学过了哪些基本事实呢?
.
垂直
3.同一平面内,过一点有且只有一条直线与已知直线垂直
.
平行
4.过直线外一点有且只有一条直线与这条直线平行
1
2
∠1=∠2
5.两条直线被第三条直线所截,如果同位∠相等,那么这两条直线平行
新知探究
逻辑推理的过程——证明
以上五条基本事实,就像数学大厦的基石一样,是无需加以论证的“起点”命题,虽然简单,却是接下来进行复杂推理的坚实依据。
但当我们遇见新的、不显而易见的数学问题时,该怎么办呢?
这时候就需要证明,什么是证明呢?
定义、基本事实为依据
逻辑推理
新结论、命题
证明
新知探究
开启证明之旅:几何推理的探索与实践
以上我们知道了何为证明,那么如何证明?我们以证明“对顶角相等”为例。
分析:首先我们要先明确该命题的条件和结论。
条件:如果两个角是对顶角
结论:那么这两个角相等
同时为了推理过程更加精确、简约,便于论证,
文字语言的条件和结论
图形语言和符号语言
如图,如果AB, CD交于点O,∠AOC与∠BOD是对顶∠,那么∠AOC=∠BOD
该命题是否正确呢?
新知探究
开启证明之旅:几何推理的探索与实践
例1:如图,已知AB, CD交于点O,∠AOC与∠BOD是对顶角。
求证:∠AOC=∠BOD
证明:因为直线AB,CD相交于点O
(已知)
所以∠AOC + ∠AOD = 180°,∠BOD + ∠AOD = 180°
(平角的定义)
所以∠AOC + ∠AOD = ∠BOD + ∠AOD
(等量代换)
所以∠AOC = ∠BOD
(等式的基本性质)
巧用“等量代换”,架起等式桥梁是解决本题的关键,,要想精确且简明的表示出这一步来,图像是必不可少的
方法技巧
新知探究
1.定理的定义与属性
开启证明之旅:几何推理的探索与实践
2.几何证明步骤(概括与表达)
定义
我们把推理证实过的真命题叫做定理
例如
对顶角相等
属性
定理和基本事实一样,也可以作为证明的依据
一
二
三
根据题意,画出图形
结合图形,写出“已知”“求证”
写出“证明”
根据以上的证明过程,我们可以得出以下结论:
下面我们试试将刚刚总结的步骤运用于实际证明中
新知探究
证明:等角的余角相等
已知: ∠α = ∠β,∠1 是∠α 的余角,∠2 是∠β 的余角。
求证:∠1 = ∠2。
证明:因为∠1 是∠α 的余角,∠2 是∠β 的余角
(已知)
所以∠1 + ∠α = 90°,∠2 + ∠β = 90°
(余角的定义)
所以∠1 + ∠α = ∠2 + ∠β
(等量代换)
因为∠α = ∠β
(已知)
所以∠1 = ∠2
(等式的基本性质)
方法技巧
解决本题的核心是用“余角定义”搭建数量关系,用“等量代换+等式性质”完成逻辑推导
即时训练
1.阅读证明过程,并在括号内填写推理依据。
如图,B,C 是线段 AD 上的两点,且 AB = CD。求证:AC = BD。
证明:因为 AB = CD
所以 AB + BC = CD + BC
所以 AC = BD
已知
等式的基本性质
线段的和的定义
提分笔记
这道题渗透了“从已知条件出发,结合基本性质与图形定义推导结论”的几何证明思维,,这种“条件→性质→结论”的逻辑链会反复用到
( )
( )
( )
即时训练
2.如图,∠ABC = ∠A'B'C',BD 和 B'D' 分别是∠ABC 和∠A'B'C'的平分线。
求证:∠ABD = ∠A'B'D'。
证明:因为 BD 是∠ABC 的平分线
(已知)
所以∠ABD =∠ABC
(角平分线的定义)
同理,B'D' 是∠A'B'C' 的平分线
(已知)
所以∠A'B'D' = ∠A'B'C'
(角平分线的定义)
又因为∠ABC = ∠A'B'C'
(已知)
所以 ∠ABC = ∠A'B'C'
(等式的基本性质)
所以∠ABD = ∠A'B'D'
(等量代换)
“等量代换”是几何证明的“桥梁工具”,当直接证两个量相等困难时,找“中间共同量”串联逻辑。
课堂小结
几何证明的三步法:思维转化的完整链条
画图
写已知求证
证明
以上证明过程并非机械流程,而是体现
直观
抽象
逻辑
特别是在证明这一步时,一般使用的演绎推理(如三段论)串联论据,构建“前提”的逻辑链
如在“等角的余角相等”的证明中,就用了使用了这样的逻辑链
余角定义
等量代换
等式的性质
课堂练习
能力提升
1.如图,直线AB,CD相交于点O,其中∠AOC是直角。
求证:∠BOC,∠BOD,∠AOD都是直角。
证明:因为AB是一条直线
(已知)
所以∠BOC = 180° - ∠AOC = 180° - 90° = 90°
(等式的性质)
所以∠BOC是直角
所以∠AOC + ∠BOC = 180°
(邻补角性质)
(直角定义)
因为∠BOD与∠AOC是对顶角
(对顶角的定义)
所以∠BOD=∠AOC=90°
(对顶角的性质)
同理∠AOD是直角
所以∠BOD是直角
(直角定义)
(对顶角的定义与性质)
在数学证明中,“同理” 是一种常用的表达方式,但它是一把双刃剑——用得恰当可以精简证明,避免重复用得不恰当则会导致逻辑漏洞、表述不清,甚至完全错误;
课堂练习
2.参考等角的余角相等的过程,证明:等角的补角相等
已知: ∠α = ∠β,∠1 是∠α 的补角,∠2 是∠β 的补角。
求证:∠1 = ∠2。
证明:因为∠1 是∠α 的补角,∠2 是∠β 的补角
(已知)
所以∠1 + ∠α = 180°,∠2 + ∠β = 180°
(补角的定义)
所以∠1 + ∠α = ∠2 + ∠β
(等量代换)
因为∠α = ∠β
(已知)
所以∠1 = ∠2
(等式的基本性质)
条件:如果两个角相等 结论:那么它们的补角相等
方法技巧
类比“等角的余角相等”这一命题的证明,发现两个题都用到了等量代换,和等式的性质
能力提升
课堂练习
3.说明“如果一个三位数的三个数位上的数字的和能被3整除,那么这个三位数能被3整除”是真命题
证明:设该三位数的百位数字为 ,十位数字为 ,个位数字为 =3k(k为整数,a,b,c均为0-9的整数)
这个三位数可以表示为
(已知)
(三位数的数值展开式)
(加法结合律)
因为9和99是3的倍数
(3的倍数的定义)
所以99a+9b=3(33a+3b),其中(33a+3b)是整数
(整数的定义)
=3[(33a+3b)+k]
(乘法分配律)
所以这三位数能被3整除
解题的关键:
拆分法:将一个数拆分为两个或多个数的和,如 100a=99a+a
10b=9b+b
拓展延伸
课堂练习
变式训练
4.,OC是∠AOB内部可绕点转动的射线,平分,平分。
求证
因为 平分 ,OE 平分 (已知)
所以 ,(角平分线的定义)
因为(角的和的定义)
所以(等量代换)
=(∠AOC+∠BOC)(乘法分配律)
=∠AOB(等量代换)
=α(等量代换)
角平分线的“双向性”:
角平分线既是“拆分工具”(将大角拆为两个相等的小角),也是“合成工具”(两个相等小角的和等于大角)。证明中常作为“等量代换”的依据。
课堂总结
1.什么是证明?
以定义、基本事实为依据,通过逻辑推理的方式得到新命题与结论的过程,叫做证明
2.几何证明步骤
根据题意,画出图形
结合图形,写出“已知”“求证”
写出“证明”
感谢聆听!
同课章节目录
