小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学苏教版
文档属性
| 名称 | 小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 709.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-15 20:02:03 | ||
图片预览




文档简介
小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学苏教版
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.5∶( )===( )%=1.25。
2.把一个棱长为6分米的正方体木块削成一个最大的圆锥,这个圆锥的体积是( )立方分米。
3.小东看一本故事书,第一天看了全书的20%,第二天看了24页,两天看了54页。这本故事书有( )页。
4.如图,以点O为圆心的圆内,三角形AOB一定是等腰三角形,作出这个判断的依据是 。
5.太平洋是世界上最大、最深的海洋,总面积为181344000平方千米,横线上的数读作:( ),改写成用“万”作单位的数是( )万平方千米。
6.3.05升=( )升( )毫升,35公顷=( )平方千米。
7.学校合唱队男生有m人,女生人数是男生的4倍,学校合唱队一共有( )人;如果男生有6人,则学校合唱队一共有( )人。
8.如果x=y(x、y均不等于0。)那么x∶y=( )∶( )。
9.勤劳智慧的中国人“可上九天揽月,可下五洋捉鳖”。自2011年首次实现“神舟号”飞船与“天宫号”空间站交会对接以来,我国的交会对接技术经历了从44小时到约6小时快速对接的跨越,创造了世界纪录。现在快速对接时间约占原来对接时间的。
10.( )∶20=0.75=( )÷8==( )%。
11.把一根长1.5米的圆柱形钢材沿横截面截成三段后,表面积比原来增加了9.6平方分米,这根钢材原来的体积是( )立方分米。
12.陈老师做实验,将含糖率为10%的40克热糖水里又放入一些糖和5克热水,搅拌均匀,此时的糖水含糖量为18%。陈老师又放入( )克糖。
13.自2013年10月1日起,某省财产继承公证费大幅度降低,由原来按固定比例收取,改为分段递减累计收取(见下表)。
施行新标准后,继承一套总价值为100万元的房屋至少能省 万元。
14.=( )%=7∶10=( )折=( )÷50。
15.探索与发现。
数学中,我们经常用平移、旋转等方式将不规则图形转化成规则图形。观察如表中每组图形与算式的变化,你有什么发现?
图形 ……
算式 1×3+1=22 2×4+1=32 3×5+1=42 …
根据发现的规律填空:
(1)4×6+1=( )2,16×18+1=( )2。
(2)( )×( )+1=20242。
16.两个同样的量杯原来各盛有640mL水。现将两个等底等高的圆柱与圆锥零件分别放入这两个量杯中,圆柱放入后量杯水面刻度如图①所示,那么图②中圆锥放入后量杯水面刻度显示应是( )mL。
17.向阳小学六年级同学参加课外兴趣小组分布情况如图:
(1)参加其他兴趣小组的同学占六年级学生总数的( )%;
(2)如果参加美术小组的有65人,那么六年级参加课外兴趣小组的同学共有( )人。
18.2022年第一季度,包河区实现地区生产总值(又称GDP)33830000000元,总量城区第一,横线上的数读作( ),改写成以“亿”作单位的数是( )亿。
19.用一根48分米的铁丝做一个长方体框架,使它的长、宽、高的比是5∶4∶3,在这个长方体框架外面糊一层纸,至少需要( )平方分米的纸。它的体积是( )立方分米。
20.2024年“五一”假日期间,溧水共接待游客799500人次,同比增长27.9%,将横线上的数改写成用“万”作单位的数是( )万人;实现旅游收入679000000元,同比增长4.14%,将横线上的数省略“亿”后面的尾数约是( )亿元。
21.观察下列等式,你会发现一些规律,依照你发现的规律,请在最后一个等式的括号里填上相同的数。
3+1=3×1,2+1=2×1,1+3=1×3,…,1+( )=1×( )。
22.三条边长分别是6厘米、8厘米、10厘米的直角三角形,将它的最短边对折与斜边相重合(如下图),那么,图中阴影部分面积是( )平方厘米。
23.中的“5”表示5个( ),8.006中的“6”表示6个( )。
24.如图,用边长1厘米的小正方形像上面这样拼摆。照这样摆下去,第6个图形的面积是( )平方厘米,第n个图形的周长是( )厘米。
25.6.4957用四舍五入法保留两位小数约是( ),保留三位小数约是( )。
26.将改写成数值比例尺是( )∶( );在一幅以它做比例尺的地图上,图上距离和实际距离成( )比例。
27.一个圆柱体的底面直径和高都是2厘米,它的侧面积是( )平方厘米,表面积是( )平方厘米,体积是( )立方厘米。
28.将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的体积最大是 立方厘米。
29.陈明用圆规和直尺画半圆,他将圆规两脚间的距离定为4厘米,画出的半圆的周长是( )厘米。
30.30比( )少40%,20比15多。
31.0.875=( )∶4=÷( )=( )%。
32.阳光小学组织安全意识知识竞赛,共20题。评分规则是答对一题得10分,答错一题扣5分,弃权不扣也不加。芳芳小组弃权两道,得了120分,他们答对了( )题。
33.把一根4米长的钢管平均锯成5段,每段是全长的,每段长( )米。
34.在50以内,6和8的公倍数有 ;9和27的最大公因数是 。
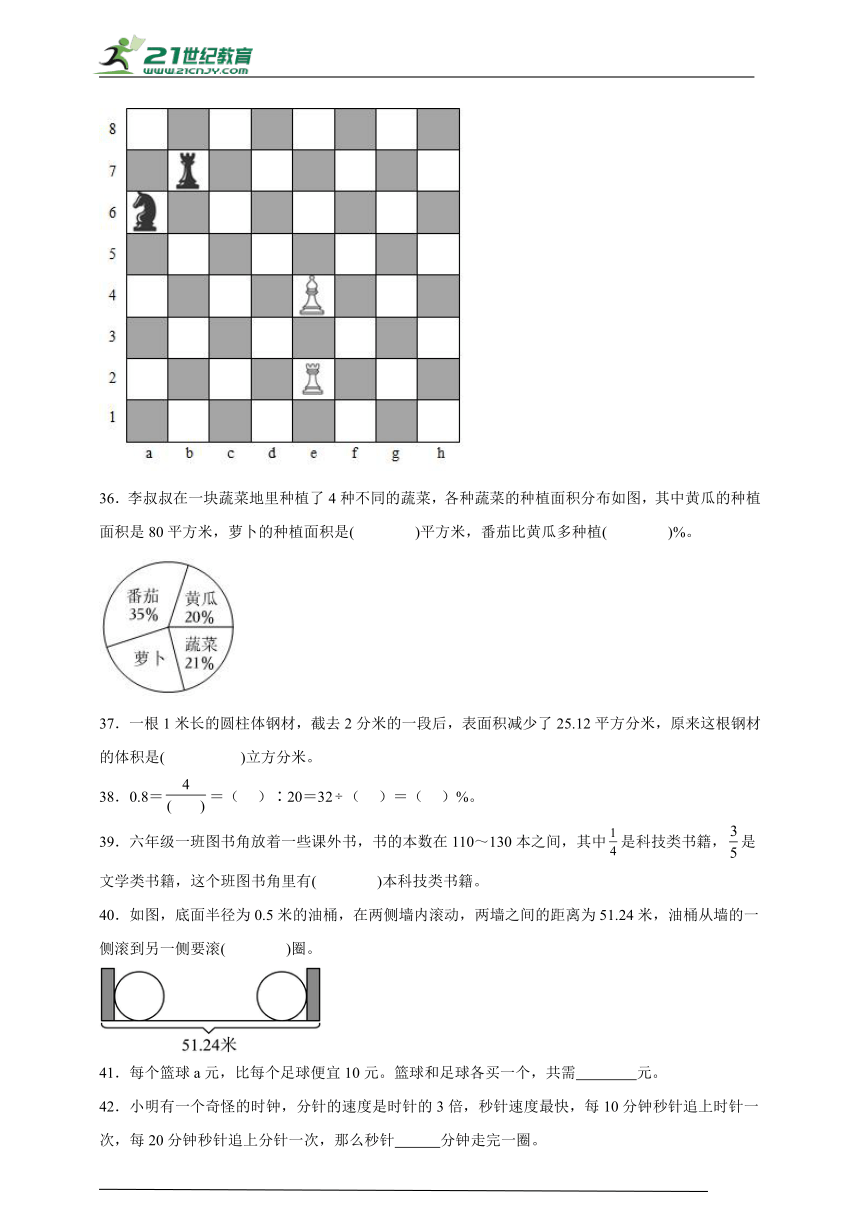
35.如图的国际象棋棋盘上,白棋“”的位置可以记录为“e4”,它向上走一格,可以记录为e4~e5。黑棋“”先向右走5格,再向下走2格,可以记录为 ~ 。
36.李叔叔在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图,其中黄瓜的种植面积是80平方米,萝卜的种植面积是( )平方米,番茄比黄瓜多种植( )%。
37.一根1米长的圆柱体钢材,截去2分米的一段后,表面积减少了25.12平方分米,原来这根钢材的体积是( )立方分米。
38.0.8==( )∶20=32( )=( )%。
39.六年级一班图书角放着一些课外书,书的本数在110~130本之间,其中是科技类书籍,是文学类书籍,这个班图书角里有( )本科技类书籍。
40.如图,底面半径为0.5米的油桶,在两侧墙内滚动,两墙之间的距离为51.24米,油桶从墙的一侧滚到另一侧要滚( )圈。
41.每个篮球a元,比每个足球便宜10元。篮球和足球各买一个,共需 元。
42.小明有一个奇怪的时钟,分针的速度是时针的3倍,秒针速度最快,每10分钟秒针追上时针一次,每20分钟秒针追上分针一次,那么秒针 分钟走完一圈。
43.3÷10=9∶( )( )÷120=( )%。
44.三角形的面积和平行四边形的面积相等,底也相等。平行四边形的高是6分米,三角形的高是( )分米。
45.有96名少年队员在一次夏令营活动中要过一条小河去爬山。现在只有一条可乘6人的橡皮艇(包括划船的同学),过一次河需要2分钟。全体队员渡到河对岸至少需要 分钟。
46.一个三位数既是2的倍数,又是3的倍数,而且又有因数5,这个三位数最大是( ),把它分解质因数是( )。
47.∶化成最简单的整数比是( ),比值是( )。
48.某小区连续三天举办公益活动,第1天来了190人,第2天来了130人,第3天来了180人,前两天都参加的有30人,后两天都参加的有40人,那么一共至少有 人来参加公益活动。
49.写出16的所有因数:( ),选择其中的四个数组成一个比例( )。
50.据统计,截至北京时间6月16日24时,全球新冠肺炎确诊病例上升至537530094例,这个数读作( ),保留一位小数大约是( )亿。
51.将班上的47名同学按照、、、、、、、、、、、、、……的顺序贴上标签,则最后一名学生的标签为 。
52.人体正常体温(腋下温度)平均为,如果我们把体温标准定在,可记作,那么35.7℃可以记作 ℃,37.3℃可以记作 ℃。
53.( )分=1.5时 0.75平方千米=( )公顷
54.习近平总书记在全国教育大会上提出教育要“五育并举”,阳光小学开展了丰富多彩的“劳动教育”实践活动。下图是该校六年级学生参加“劳动教育”实践活动情况的统计图,参加烹饪小组的人数占总人数的( )%,如果六年级参加“劳动教育”实践活动的一共有120人,那么参加手工小组的有( )人。
55.渔船在海上遇险,向救援中心发送遇险位置的求救信号应该是:渔船在海鸟岛的( )偏( )( )°方向( )千米处。
56.( )∶20==( )÷36==( )%=( )折。
57.两根长短粗细不同的蜡烛,短的可燃8小时,长的可燃的时间是短的,同时点燃两根蜡烛,经过3小时,它们长短正好相等,未点燃之前,短蜡烛比长蜡烛短( )。
58.如图,把打乱的积木拼图还原,要把1号积木向右平移( )格,把2号积木绕点A逆时针旋转( )°。
59.如图,将一个高6厘米的圆柱转化成长方体,表面积增加了48平方厘米,这个圆柱的底面半径是( )厘米。
60.小静打开数学书时,发现两页页码之积是420,这两页分别是( )页和( )页。
《小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
1.4;15;;125
【分析】小数化成分数,两位小数先化成分母为100的分数,再化简成最简分数;
分数与比的关系:分子相当于比的前项,分母相当于比的后项,分数线相当于比号;
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号。
【详解】1.25==
=5∶4
==
1.25=125%
即5∶4===125%=1.25。
(第三个空答案不唯一)
【点睛】掌握小数、分数、百分数的互化、分数的基本性质、分数与比的关系是解题的关键。
2.56.52
【分析】这个圆锥的底面直径是6分米,高是6分米,再根据圆锥的体积=底面积×高÷3,解答即可。
【详解】6÷2=3(分米)
3.14×3×3×6÷3
=9.42×3×6÷3
=28.26×6÷3
=169.56÷3
=56.52(立方分米)
这个圆锥的体积是56.52立方分米。
【点睛】熟练掌握圆锥的体积公式,是解答此题的关键。
3.150
【分析】先计算出第一天看书的页数,用第一天看书的页数除以20%,即为这本书的总页数,据此解答。
【详解】(54-24)÷20%
=30÷20%
=150(页)
【点睛】解答本题的关键是明确已知一个数的百分之几是多少,求这个数,用除法计算。
4.见详解
【分析】等腰三角形的两条腰相等。从图中可知,OA和OB都是圆的半径,那么OA=OB,据此判断三角形AOB是等腰三角形。
【详解】图中三角形AOB一定是等腰三角形,作出这个判断的依据是OA和OB都是圆的半径,同一个圆的半径相等。
5. 一亿八千一百三十四万四千 18134.4
【分析】根据整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位有一个或连续几个0,都只读一个零,据此读出此数;
改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字。
【详解】181344000读作:一亿八千一百三十四万四千
181344000=18134.4万
太平洋是世界上最大、最深的海洋,总面积为181344000平方千米,横线上的数读作:一亿八千一百三十四万四千;改写成用“万”作单位的数是18134.4万平方千米。
6. 3 50 0.35/
【分析】根据1升=1000毫升,1平方千米=100公顷,高级单位转化为低级单位乘进率,低级单位转化为高级单位除以进率,单名数换复名数,整数部分填在高级单位中,小数部分乘进率转化为低级单位,据此解答。
【详解】(1)3.05升=3升+0.05升
0.05×1000=50(毫升)
3.05升=3升50毫升
(2)35÷100=0.35(平方千米)
35公顷=0.35平方千米
7. 5m 30
【分析】根据求一个数的几倍是多少,用这个数乘倍数,据此用m×4求出学校合唱队女生有多少人,再加上男生人数就是合唱队一共有多少人;把男生人数代入上一步求出的关系式进行计算即可。
【详解】4×m=4m(人)
4m+m=5m(人)
当m=6时,
5m=5×6=30(人)
所以学校合唱队一共有5m人;如果男生有6人,则学校合唱队一共有30人。
8. 5 6
【分析】根据比例的基本性质:两内项之积等于两外项之积,写出这个比例式;化简,即可解答。
【详解】x=y,
x∶y=∶
=(×15)∶(×15)
=10∶12
=(10÷2)∶(12÷2)
=5∶6
【点睛】利用比例的基本性质以及比的基本性质进行解答。
9.
【分析】根据求一个数占另一个数的几分之几,用除法计算,用现在快速对接时间除以原来对接时间,得数用分数表示,能约分的要约为最简分数。
【详解】
勤劳智慧的中国人“可上九天揽月,可下五洋捉鳖”。自2011年首次实现“神舟号”飞船与“天宫号”空间站交会对接以来,我国的交会对接技术经历了从44小时到约6小时快速对接的跨越,创造了世界纪录。现在快速对接时间约占原来对接时间的。
10.15;6;36;75
【分析】被除数=除数×商,8×0.75=6;根据小数化分数的方法,0.75=,根据分数与比的关系,比的基本性质,=3∶4=(3×5)∶(4×5)=15∶20;根据分数的基本性质,==;根据小数化百分数的方法,0.75=75%。
【详解】根据分析可得:
15∶20=0.75=6÷8==75%
【点睛】考查了小数、分数、百分数的转化方法、比的基本性质、分数的基本性质,学生应掌握。
11.36
【分析】圆柱形钢材沿横截面截成三段后,表面积比原来增加了4个横截面面积。已知表面积比原来增加了9.6平方分米,用9.6除以4即可求出圆柱的横截面面积。圆柱的体积=底面积×高,用这根钢材的横截面面积乘长即是钢材的体积。
【详解】1.5米=15分米
9.6÷4×15
=2.4×15
=36(立方分米)
【点睛】本题考查立体图形的切拼和圆柱体积的应用。明确圆柱表面积比原来增加了4个横截面面积,继而求出横截面的面积是解题的关键。
12.5
【分析】根据题意,利用糖水的质量×含糖率即可求出糖的质量,糖水里又放入一些糖和5克热水,所以糖水的质量要增加,利用含糖率=糖的质量÷糖水的质量×100%,列方程解答即可。
【详解】解:设陈老师又放入x克糖。
40×10%=4(克)
(4+x)÷(40+x+5)×100%=18%
400+100x=720+18x+90
82x=810-400
82x=410
x=5
【点睛】此题属于百分率实际应用,计算的结果最大值为100%,都是用一部分数量(或全部数量)除以全部数量乘百分之百。
13.1.06
【分析】根据百分数乘法的意义,可知调整前100万元收取(100×2%)万元;调整后20万元部分收取(20×1.2%)万元,20万元到50万元部分收取[(50-20)×1%]万元,50万元到100万元部分收取[(100-50)×0.8%]万元,然后将三部分相加,即可求出调整后,一共收取的公证费;然后用调整后的公证费减去调整前的公证费,即可求出节省的钱数。
【详解】100×2%=2(万元)
20×1.2%+(50-20)×1%+(100-50)×0.8%
=20×1.2%+30×1%+50×0.8%
=0.24+0.3+0.4
=0.94(万元)
2-0.94=1.06(万元)
继承一套总价值为100万元的房屋至少能省1.06万元。
14.30;70;七;35
【分析】根据比与分数的关系7∶10=,根据分数的基本性质,分子、分母都乘3就是;
同理,的分子、分母都乘10就是,改写成百分数是70%;
根据折扣的意义70%就是七折;
根据比与除法的关系7∶10=7÷10,再根据商不变的性质被除数、除数都乘5就是35÷50。
【详解】
=70%=7∶10=七折=35÷50
15.(1) 5 17;
(2) 2023 2025
【分析】观察所给算式1×3+1=22,2×4+1=32,3×5+1=42。对于乘法部分,第一个因数依次是1、2、3,呈现依次增加1的规律;第二个因数依次是3、4、5,比对应的第一个因数大2。等式右边是一个数的平方,这个数比乘法算式中的第一个因数大1。总结规律为:n×(n+2)+1=(n+1)2(n为自然数)然后根据此规律计算填空。
【详解】(1)4×6+1:这里n=4,根据规律(n+1)2,即4+1=5,所以4×6+1=52,16×18+1:这里n=16,16+1=17,所以16×18+1=172
4×6+1=52,16×18+1=172
(2)因为结果是20242,由规律(n+1)2=20242,可得n+1=2024,则n=2023,n+2=2023+2=2025,即2023×2025+1=20242
2023×2025+1=20242。
16.720
【分析】由图①可得,880mL=原来水640mL+圆柱的体积,因此用880-640即可求出圆柱的体积。等底等高的圆柱的体积是圆锥体积的3倍,据此用圆柱的体积除以3,求出圆锥的体积,最后用量杯原来的水的体积加圆锥的体积,可得出图②量杯水面刻度。
【详解】(880-640)÷3+640
=240÷3+640
=80+640
=720(mL)
所以图②中圆锥放入后量杯水面刻度显示应是720mL。
17.(1)22
(2)250
【分析】(1)把六年级参加各兴趣小组的人数看作单位“1”,用单位“1”减去参加体育、美术、音乐兴趣小组人数所占的百分率就是参加其它兴趣小组人数所占的百分率;
(2)根据除法的意义,用参加美术小组的人数除以所占的百分率就是六年级参加课外兴趣小组同学的总人数。
【详解】(1)1-34%-26%-18%
=66%-26%-18%
=40%-18%
=22%
参加其他兴趣小组的同学占六年级学生总数的22%。
(2)65÷26%=250(人)
六年级参加课外兴趣小组的同学共有250人。
18. 三百三十八亿三千万 338.3
【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位一个0或连续几个0都只读一个零,即可读出此数;
改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“亿”字。
【详解】33830000000读作:三百三十八亿三千万
33830000000=338.3亿
【点睛】本题主要考查整数的读法和改写,分级读即可快速、正确地读出此数,改写时要注意带计数单位。
19. 94 60
【分析】长方体的棱长和=(长+宽+高)×4,据此用长方体的棱长和除以4,求出长、宽、高的和,把长、宽、高的比看作份数比,用长、宽、高的和除以份数和,求出1份是多少分米,再分别乘长、宽、高各自的份数,求出长、宽、高分别是多少分米,再根据长方体的表面积=(长×宽+宽×高+长×高)×2,长方体的体积=长×宽×高,代入数据解答即可。
【详解】长、宽、高的和:
48÷4=12(分米)
总份数:
5+4+3=12(份)
12×=5(分米)
12×=4(分米)
12×=3(分米)
表面积:
(5×4+4×3+5×3)×2
=(20+12+15)×2
=47×2
=94(平方分米)
体积:5×4×3
=20×3
=60(立方分米)
故至少需要94平方分米的纸,它的体积是60立方分米。
20. 79.95 7
【分析】改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;
省略“亿”后面的尾数求它的近似数,要把亿位的下一位千万位上的数进行四舍五入,再在数的后面写上“亿”字。
【详解】799500=79.95万
679000000≈7亿
2024年“五一”假日期间,溧水共接待游客799500人次,同比增长27.9%,将横线上的数改写成用“万”作单位的数是79.95万人;实现旅游收入679000000元,同比增长4.14%,将横线上的数省略“亿”后面的尾数约是7亿元。
21. 2 2
【分析】先把带分数化成假分数,再找规律,即+=,,,观察可知两个分数的分子相同,且是两个分母的和,根据此规律可求解。
【详解】+=,,,观察可知两个分数的分子相同,且是两个分母的和,所以,即1+2=1×2,
【点睛】本题主要考查“式”的规律,先变化原式,再发现规律,根据规律解答。
22.6
【分析】如图:根据题意得BD=BC=6厘米,AD=AB-BD=10-6=4厘米,因为三角形ADE的面积=×AD×DE,三角形BDE的面积=×BD×DE,所以三角形ADE的面积∶三角形BDE的面积=AD∶BD=4∶6=2∶3,又因为三角形ABC的面积=×6×8=24(平方厘米),所以三角形ADE的面积==6(平方厘米)。
【详解】根据分析得,BD=6(厘米)
AD=10-6=4(厘米)
三角形ADE的面积∶三角形BDE的面积∶三角形BCE=AD∶BD∶BC=4∶6∶6=2∶3∶3
三角形ABC的面积=×6×8=24(平方厘米)
三角形ADE的面积==6(平方厘米)
【点睛】此题主要考查等底等高的三角形面积相等,关键是找准面积的比。
23. 千分之一
【分析】根据分数的意义及每个数位上的数代表不同的计数单位,据此解答。
【详解】中的“5”表示5个,8.006中的“6”表示6个千分之一。
【点睛】本题主要考查了分数的意义及小数计数单位的认识。
24. 21 4n
【分析】观察可得规律:第1个图形面积是1平方厘米,第2个图形面积是(1+2)平方厘米,第3个图形面积是(1+2+3)平方厘米……,第n个图形面积是(1+2+3+…+n)平方厘米,据此得出第6个图形的面积。
第1个图形周长是4厘米,第2个图形周长是8厘米,第3个图形周长是12厘米……,据此得出第n个图形的周长。
【详解】第6个图形的面积是:1+2+3+4+5+6=21(平方厘米)
第1个图形的周长是:4×1=4(厘米)
第2个图形的周长是:4×2=8(厘米)
第3个图形的周长是:4×3=12(厘米)
……
第n个图形的周长是:4×n=4n(厘米)
因此第6个图形的面积是21平方厘米,第n个图形的周长是4n厘米。
25. 6.50 6.496
【分析】保留两位小数看千分位,保留三位小数看万分位,小于5直接舍去,大于或等于5向前一位进一,据此保留近似数。
【详解】
6.4957用四舍五入法保留两位小数约是6.50,保留三位小数约是6.496。
26. 1 2000000 正
【分析】由线段比例尺可知,图上距离1厘米相当于实际距离20千米,根据“图上距离∶实际距离=比例尺”改写成数值比例尺,注意单位的换算:1千米=100000厘米。
判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】改写成数值比例尺是:
1厘米∶20千米
=1厘米∶(20×100000)厘米
=1∶2000000
因为图上距离∶实际距离=比例尺(一定),比值一定,所以图上距离和实际距离成正比例。
【点睛】本题考查线段比例尺和数值比例尺的转化,正、反比例的意义及辨识方法,掌握图上距离、实际距离、比例尺之间的关系是解题的关键。
27. 4π 6π 2π
【分析】根据圆柱的表面积公式S表=S侧+2S底,其中S侧=πdh,S底=πr2;根据圆柱的体积公式V=Sh,代入数据计算即可。
【详解】圆柱的侧面积:
π×2×2=4π(平方厘米)
圆柱的底面积:
π×(2÷2)2=π(平方厘米)
圆柱的表面积:
4π+2π=6π(平方厘米)
圆柱的体积:
π×2=2π(立方厘米)
【点睛】掌握圆柱的侧面积、表面积、体积计算公式是解题的关键。
28.150.72
【分析】(1)以4厘米的边为轴旋转时,它的底面半径是3厘米,高是4厘米,再根据圆柱的体积公式可求出它的体积;
(2)以3厘米的边为轴旋转时,它的底面半径是4厘米,高是3厘米,再根据圆柱的体积公式可求出它的体积。
再比较大小即可求解。
【详解】(1)以4厘米的边为轴旋转时,它的体积是:
3.14×32×4
=3.14×9×4
=113.04(立方厘米)
(2)以3厘米的边为轴旋转时,它的体积是:
3.14×42×3
=3.14×16×3
=150.72(立方厘米)
150.72>113.04
将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的最大体积是150.72立方厘米。
29.20.56
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径的长度,根据半圆的周长公式:C=πr+2r,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
【点睛】此题主要考查半圆周长公式的灵活运用,关键是熟记公式。
30.50;
【分析】(1)把要求的数看作单位“1”,30相当于要求数的(1-40%),根据已知一个数的百分之几是多少,求这个数,用除法解答;
(2)把15看作单位“1”,先求出20比15多多少,再根据求一个数是另一个数的几分之几,用除法解答。
【详解】(1)30÷(1-40%)
=30÷0.6
=50
30比50少40%。
(2)(20-15)÷15
=5÷15
=
20比15多。
【点睛】此题考查的目的是理解掌握分数、百分数的乘法、除法的计算法则,并且能够正确熟练地进行计算。
31.3.5;24;;87.5%
【分析】0.875化成分数化简后就是;根据分数的基本性质,的分子、分母同时乘4就是,32-8=24;根据除法各部分之间的关系,除数=被除数÷商,÷=;根据比值=比的前项÷比的后项,即比的前项=比值×比的后项,0.875×4=3.5;0.875的小数点向右移动两位,同时添上百分号可化成87.5%。
【详解】0.875=3.5∶4=÷=87.5%
【点睛】此题考查小数、分数、百分数、比和除法之间的转化,根据它们之间的关系和性质进行转化。
32.14
【分析】根据“每做对一道得10分,答错扣5分,”可知:答错一题比答对一题少得10+5=15分;假设芳芳小组全部答对得分是10×18=180(分),比120分多得180-120=60(分),那么他们答错了:60÷(10+5)=4(道);所以芳芳小组答对:18-4=14道题。
【详解】[10×(20-2)-120]÷(10+5)
=[10×18-120]÷15
=[180-120]÷15
=60÷15
=4(道)
20-2-4
=18-4
=14(道)
【点睛】鸡兔同笼问题一般利用解设法解答,本题先假设全部答对,得出与实际得分的差就是每道错题对应的失分,从而求出错题数。
33.;
【分析】求每段是全长的几分之几,就是将这段钢管长看作单位“1”,平均分成5份,表示其中的一份;求每段长多少米,就是将4米平均分成5段,求一段长多少米,据此解答。
【详解】1÷5
4÷5(米)
把一根4米长的钢管平均锯成5段,每段是全长的,每段长米。
34. 24、48 9
【分析】公倍数是两个数公有的倍数,先找出两个数的倍数,从中找出公有的倍数;
公因数是两个数公有的因数,先求出两个数的因数,然后找出公有的因数即可,公因数中最大的一个就是这两个数的最大公因数,据此找出9和27的最大公因数。
【详解】(1)50以内6和8的倍数是:
6的倍数是:6、12、18、24、30、36、42、48,
8的倍数是:8、16、24、32、40、48,
50以内6和8的公倍数有:24、48;
(2)9的因数有:1、3、9,
27的因数有:1、3、9、27,
9和27的公因数有:1、3、9;9和27的公因数1、3、9中,9是最大的,所以9和27的最大公因数是9。
【点睛】此题需要学生掌握倍数、公倍数、因数、公因数和最大公因数的意义和求法。
35. b7 g5
【分析】由题意得,位置的记法是“先列后排”,黑棋“”先向右走5格,再向下走2格,本来在b7的位置,现在到了g5的位置,据此解答即可。
【详解】黑棋“”先向右走5格,再向下走2格,可以记录为b7~g5。
【点睛】此题考查了用数对表示位置在实际当中的运用。明确棋子前后位置的数对是解题的关键。
36. 96 75
【分析】以这块地的面积为单位“1”,已知黄瓜的种植面积是80平方米,占这块地的面积的20%,根据已知一个数的百分之几是多少,求这个数用除法计算,求出这块地的面积。
萝卜的种植面积占这块地的(1-35%-20%-21%),根据求出一个数的几分之几是多少,用乘法计算,用这块地的面积×(1-35%-20%-21%),求出萝卜的种植面积。
已知番茄种植面积占这块地的35%,用这块地的面积×35%,求出番茄的种植面积。根据求一个数比另一个数多百分之几,用除法计算,以黄瓜的种植面积为单位“1”,用番茄比黄瓜多种植的面积÷黄瓜的种植面积即可求出番茄比黄瓜多种植百分之几。
【详解】80÷20%=400(平方米)
400×(1-35%-20%-21%)
=400×24%
=96(平方米)
400×35%=140(平方米)
(140-80)÷80
=60÷80
=0.75
=75%
因此,萝卜的种植面积是96平方米,番茄比黄瓜多种植75%。
37.125.6
【分析】截去2分米的一段后,表面积减少的部分正好是这段2分米钢材的侧面积,用侧面积除以高,求出底面圆的周长,利用圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,求出底面半径,再根据圆柱的体积公式:体积=底面积×高,计算出体积。
【详解】1米=10分米
25.12÷2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(分米)
3.14×22×10
=3.14×4×10
=12.56×10
=125.6(立方米)
一根1米长的圆柱体钢材,截去2分米的一段后,表面积减少了25.12平分方米,原来这根钢材的体积是125.6立方米。
【点睛】本题考查圆柱表面积及体积的计算方法,根据表面积减少情况计算出原钢材的底面半径,再结合钢材的长进一步计算出体积,注意单位名数的换算。
38.5;16;40;80
【分析】先把0.8化成分数,0.8==;根据分数与比的关系、分数的基本性质,把的分子和分母同时乘4,得==16∶20;根据分数与除法的关系,把的分子和分母同时乘8,得==32÷40;把0.8的小数点向右移动两位,化成百分数为80%。
【详解】0.8==16∶20=32÷40=80%。
【点睛】本题考查了分数、小数和百分数的互化,分数与除法、比的关系,分数的基本性质等,要牢固掌握相关知识并熟练运用。
39.30
【分析】根据题意,图书角书的数量必须能平均分成4和5份,也就是书的本数必须是4和5的倍数,找出在110到130之间4和5的公倍数即可求出总本数,再乘,即可求出这个班图书角里有多少本科技类书籍。
【详解】4×5=20
20×6=120(本)
120×=30(本)
这个班图书角里有30本科技类书籍。
【点睛】本题考查公倍数的计算及分数乘法的计算和应用。理解题意,找出数量关系,列式计算即可。
40.16
【分析】油桶每滚一圈经过的距离也就是圆形油桶的周长,根据圆的周长=2πr,代入数值计算出油桶滚一圈经过的距离;其中油桶滚动的距离=两墙之间的距离-油桶底面的直径,最后用油桶滚动的距离除以圆的周长,所得结果即为油桶要滚的圈数。
【详解】(51.24-0.5×2)÷(2×3.14×0.5)
=(51.24-1)÷3.14
=50.24÷3.14
=16(圈)
因此油桶从墙的一侧滚到另一侧要滚16圈。
41.(2a+10)/(10+2a)
【分析】每个篮球a元,比每个足球便宜10元。每个足球是(10+a)元,篮球和足球各买一个,共需多少元,用加法列式并化简即可解答。
【详解】a+(10+a)=2a+10(元)或10+2a(元)
每个篮球a元,比每个足球便宜10元。篮球和足球各买一个,共需(2a+10)或(10+2a)元。
42.
8
【分析】根据题意可以设时针速度为度/分钟,分针速度为 度/分钟,秒针速度为 度/分钟。
根据秒针每10分钟追上时针一次,也就是当秒针和时针在同一地点出发时,秒针的速度快,时针的速度慢,当秒针追上时针时,秒针比时针都走一圈,也就是360°,即得方程:;
同理每20分钟追上分针一次,得方程:。联立方程解得,秒针一圈是360°,则除以秒针的速度就是秒针的时间。
【详解】解:设时针速度为度/分钟,则分针速度为度/分钟,秒针速度为度/分钟。
秒针追上时针:
①
秒针追上分针:
②
将①式和②式相减
代入①得:
(分钟)
则秒针8分钟走完一圈。
【点睛】找到秒针、分针、时针三者之间的数量关系式,联立两个方程找出秒针的速度,最后得出时间。
43.30;50;36;30
【分析】根据比与除法的关系3÷10=3∶10,再根据比的性质比的前、后项都乘3就是9∶30;根据分数与除法的关系3÷10,再根据分数的基本性质,分子、分母都乘5就是;根据商不变的性质,3÷10的被除数、除数都乘12就是36÷120;3÷10=0.3,把0.3的小数点向右移动两位添上百分号就是30%。
【详解】3÷10=3∶10=(3×3)∶(10×3)=9∶30
3÷10=
因此,3÷10=9:3036÷120=30%。
44.12
【分析】等面积等底的平行四边形和三角形,三角形的高是平行四边形高的2倍,直接用平行四边形的高×2=三角形的高,据此列式计算。
【详解】6×2=12(分米)
三角形的高是12分米。
45.74
【分析】要想过河所用时间最少,则每次尽可能坐满,派出一个同学来划船,则每次剩下5个位置,95÷5即可求出有几个5,也就是需要送几次,也就是19次,而划船的同学需要返回18次,所以船一共来回了(19+18)次,每次需要2分钟,用(19+18)×2即可求出全部人过河至少需要的时间。
【详解】96-1=95(人)
95÷5=19(次)
19+18=37(次)
37×2=74(分钟)
全体队员渡到河对岸至少需要74分钟。
【点睛】解此题关键是理解渡船就要有一个撑船的,实际上除最后一次,每次只能坐5人。
46. 990 990=2×3×3×5×11
【分析】同时是2、3和5的倍数的特征是,个位上必须是0,且各位上的数字之和是3的倍数;据此解答。
【详解】一个三位数既是2的倍数,又是3的倍数,而且又有因数5,这个三位数最大是990,
把990分解质因数:
990=2×3×3×5×11。
【点睛】此题考查的目的是理解掌握同时是2、3和5的倍数的特征,以及分解质因数的方法。
47. 9∶1 9
【分析】根据比的基本性质作答,即比的前项和后项同时乘或除以一个数(0除外),比值不变,和分母的最小公倍数是15,比的前项和后项同时乘15,将其化成最简的整数比9∶1;求比值是用比的前项除以比的后项所得的数值,也可以用最简比的前项除以后项即可得比值。
【详解】∶
=(×15)∶(×15)
=9∶1
∶===9
或9∶1=9÷1=9
所以,∶化成最简单的整数比是9∶1,比值是9。
48.
430
【分析】为了使总人数最少,应尽可能让重复参加的人数最多。
已知前两天都参加的有30人,后两天都参加的有40人。
假设三天都参加的人数最多为30人(即前两天重叠的30人全部参加了第三天),则后两天重叠的40人中,有30人三天都参加,剩余10人只参加后两天。
即第一天:190人,其中30人三天都参加,剩余160人只参加第一天。
第二天:130人,其中30人三天都参加,10人只参加后两天,剩余90人只参加第二天。
第三天:180人,其中30人三天都参加,10人只参加后两天,剩余140人只参加第三天。
通过分解各天人数并计算不重复部分,即可得到总人数。
【详解】190-30=160(人)
130-30-10=90(人)
180-30-10=140(人)
160 +90 +140 +30+10 =430(人)
则一共至少有430人来参加公益活动。
【点睛】总数最少就是让重复参加的人最多,重复参加最多的有30人,分别在求出三天只参加的人数,再加上重复的人数即可得出最少情况下的人数。
49. 1,2,4,8,16 1∶2=4∶8
【分析】找一个数的因数的方法:列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。
表示两个比相等的式子叫做比例。根据比例的意义,从16的因数中选择四个数,分别求出两个数的比值,比值相等的能组成比例;反之,比值不相等的,就不能组成比例。
【详解】16=1×16=2×8=4×4,所以16的因数有:1,2,4,8,16;
1∶2=1÷2=0.5
4∶8=4÷8=0.5
比值相等,所以1,2,4,8可以组成一个比例,如:1∶2=4∶8。
填空如下:
写出16的所有因数:(1,2,4,8,16),选择其中的四个数组成一个比例(1∶2=4∶8)。(最后一个空答案不唯一)
50. 五亿三千七百五十三万零九十四 5.4
【分析】从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零,即可读出此数;改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,再用“四舍五入”法保留一位小数,最后在数的后面写上“亿”字。
【详解】537530094读作:五亿三千七百五十三万零九十四;
保留一位小数大约是:537530094=5.37530049亿≈5.4亿。
【点睛】本题主要考查多位数的读法和求近似数,读数时要注意零的读法,求近似数时要注意带计数单位。
51.B
【分析】通过观察发现,是按照A、B、C、D、A这样的方式每5个循环的。利用除法,即可求出47名学生里面有9个这样的循环剩下的2个人分别是A和B。
【详解】47÷5=9(组)……2(人)
则最后一名学生的标签为B。
52. ﹣0.8 ﹢0.8/0.8
【分析】正负数表示一组相反意义的量,根据题意,比36.5℃高的部分记作正数,在数字前加上“﹢”号,也可不加。比36.5℃低的部分记作负数,在数字前加上“﹣”号。据此解答。
【详解】36.5℃-35.7℃=0.8℃
37.3℃-36.5℃=0.8℃
人体正常体温(腋下温度)平均为,如果我们把体温标准定在,可记作,那么35.7℃可以记作﹣0.8℃,37.3℃可以记作﹢0.8℃(或0.8℃)。
53. 90 75
【分析】高级单位时化低级单位分乘进率60。
高级单位平方千米化低级单位公顷乘进率100。
【详解】90分=1.5时
0.75平方千米=75公顷
【点睛】此题是考查时间的单位换算、面积的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
54. 45 30
【分析】把参加“劳动教育”实践活动总人数看作单位“1”;
观察扇形统计图可知,参加手工小组的人数总人数的四分之一;所以手工小组的人数占参加“劳动教育”实践活动总人数的25%;
求参加烹饪小组人数占总人数的百分之几,用1减去参加种植小组占总人数的百分率,减去参加烹饪小组人数占总人数的百分率,即可解答;
用六年级参加“劳动教育”实践活动的总人数乘参加手工小组占总人数的百分率,即可解答。
【详解】1-30%-25%
=70%-25%
=45%
120×25%=30(人)
【点睛】根据扇形统计图提供的信息,以及求一个数的百分之几是多少的知识进行解答。
55. 北/东 东/北 30/60 62.5
【分析】(1)(2)(3)确定方向:以海岛为观测点,根据图中“北”的标识确定方向。方向描述有两种方式,一种是北偏东,用量角器测量渔船与正北方向夹角为30°,即北偏东30°;另一种是东偏北,此时渔船与正东方向夹角为60°,即东偏北60°。
(4)计算距离:已知图中比例尺为1∶2500000,意味着图上1厘米代表实际距离2500000厘米,也就是25千米。测量图上渔船到海岛的距离(假设测量后经计算对应实际距离为62.5千米,可根据比例尺进行换算得到实际距离。
【详解】(1)(2)(3)北偏东30°情况:用量角器测量得出渔船在海岛的北偏东30°方向。(4)因为比例尺1∶2500000,量得图上渔船到海岛距离为2.5厘米,实际距离为2.5×25=62.5千米。
渔船在海鸟岛的北偏东30°方向62.5千米处。
东偏北60°情况:用量角器测量得出渔船在海岛的东偏北60°方向。因为比例尺1∶2500000,量得图上渔船到海岛距离为2.5厘米,实际距离为2.5×25=62.5千米。
渔船在海鸟岛的东偏北30°方向62.5千米处。(答案不唯一)
56.15;27;9;75;七五
【分析】根据比与分数的关系=3∶4,再根据比的基本性质比的前、后项都乘5就是15∶20;根据分数与除法的关系=3÷4,再根据商不变的性质被除数、除数都乘9就是27∶36;根据分数的基本性质的分子、分母都乘3就是;3÷4=0.75,把0.75的小数点向右移动两位添上百分号就是75%;根据折扣的意义75%就是七五折。
【详解】=3∶4=(3×5)∶(4×5)=15∶20
=3÷4=(3×9)÷(4×9)=27÷36
=
=3÷4=0.75=75%
75%=七五折
15∶20==27÷36==75%=七五折
57.
【分析】短的可燃8小时,长的可燃的时间是短的,长的可燃烧的时间是8×=4小时;燃烧3小时,短蜡烛燃烧了,长蜡烛燃烧了;短蜡烛还剩1-没有燃烧,长蜡烛还有1-没有燃烧,剩下的部分相等,即短蜡烛的(1-)=长蜡烛的(1-),即短蜡烛×(1-)=长蜡烛×(1-),再根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此根据比例基本性质的逆运算,求出短蜡烛与长蜡烛的比,即求出短蜡烛是长蜡烛的几分之几,设长蜡烛长是1,求出短蜡烛,再用长蜡烛与短蜡烛的差,除以长蜡烛,即可解答。
【详解】长的蜡烛燃烧时间:8×=4(小时)
3小时短蜡烛燃烧了3÷8=,还剩1-=;
3小时长蜡烛燃烧了3÷4=,还剩1-=。
短蜡烛×=长蜡烛×
短蜡烛∶长蜡烛=∶
=(×8)∶(×8)
=2∶5
即短蜡烛是长蜡烛的。
设长蜡烛长度是1。
(1-)÷1
=÷1
=
两根长短粗细不同的蜡烛,短的可燃8小时,长的可燃的时间是短的,同时点燃两根蜡烛,经过3小时,它们长短正好相等,未点燃之前,短蜡烛比长蜡烛短。
58. 2/两 90
【分析】平移是指在平面内,将一个图形沿着某个方向移动一定的距离,这样的运动叫做图形的平移。
旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
【详解】
如图,把打乱的积木拼图还原,要把1号积木向右平移(2)格,把2号积木绕点A逆时针旋转(90)°。
59.4
【分析】将一个圆柱切拼成一个长方体,形状变了,体积不变。长方体的长相当于圆柱底面周长的一半,宽相当于圆柱的半径,高相当于圆柱的高。长方体的上下面等于圆柱的上下底面,长方体的前后面等于圆柱的侧面,表面积增加了左右面积,即增加的面积=宽×高×2=半径×高×2=48平方厘米。已知高是6厘米,据此求出半径即可。
【详解】48÷2÷6
=24÷6
=4(厘米)
这个圆柱的底面半径是4厘米。
60. 20 21
【分析】根据题意,两页页码之积是420,先把420分解质因数,再把这些质因数重新组合,变成连续两个自然数相乘的形式,即可得解。
【详解】420=2×2×3×5×7=(2×2×5)×(3×7)=20×21
这两页分别是20页和21页。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.5∶( )===( )%=1.25。
2.把一个棱长为6分米的正方体木块削成一个最大的圆锥,这个圆锥的体积是( )立方分米。
3.小东看一本故事书,第一天看了全书的20%,第二天看了24页,两天看了54页。这本故事书有( )页。
4.如图,以点O为圆心的圆内,三角形AOB一定是等腰三角形,作出这个判断的依据是 。
5.太平洋是世界上最大、最深的海洋,总面积为181344000平方千米,横线上的数读作:( ),改写成用“万”作单位的数是( )万平方千米。
6.3.05升=( )升( )毫升,35公顷=( )平方千米。
7.学校合唱队男生有m人,女生人数是男生的4倍,学校合唱队一共有( )人;如果男生有6人,则学校合唱队一共有( )人。
8.如果x=y(x、y均不等于0。)那么x∶y=( )∶( )。
9.勤劳智慧的中国人“可上九天揽月,可下五洋捉鳖”。自2011年首次实现“神舟号”飞船与“天宫号”空间站交会对接以来,我国的交会对接技术经历了从44小时到约6小时快速对接的跨越,创造了世界纪录。现在快速对接时间约占原来对接时间的。
10.( )∶20=0.75=( )÷8==( )%。
11.把一根长1.5米的圆柱形钢材沿横截面截成三段后,表面积比原来增加了9.6平方分米,这根钢材原来的体积是( )立方分米。
12.陈老师做实验,将含糖率为10%的40克热糖水里又放入一些糖和5克热水,搅拌均匀,此时的糖水含糖量为18%。陈老师又放入( )克糖。
13.自2013年10月1日起,某省财产继承公证费大幅度降低,由原来按固定比例收取,改为分段递减累计收取(见下表)。
施行新标准后,继承一套总价值为100万元的房屋至少能省 万元。
14.=( )%=7∶10=( )折=( )÷50。
15.探索与发现。
数学中,我们经常用平移、旋转等方式将不规则图形转化成规则图形。观察如表中每组图形与算式的变化,你有什么发现?
图形 ……
算式 1×3+1=22 2×4+1=32 3×5+1=42 …
根据发现的规律填空:
(1)4×6+1=( )2,16×18+1=( )2。
(2)( )×( )+1=20242。
16.两个同样的量杯原来各盛有640mL水。现将两个等底等高的圆柱与圆锥零件分别放入这两个量杯中,圆柱放入后量杯水面刻度如图①所示,那么图②中圆锥放入后量杯水面刻度显示应是( )mL。
17.向阳小学六年级同学参加课外兴趣小组分布情况如图:
(1)参加其他兴趣小组的同学占六年级学生总数的( )%;
(2)如果参加美术小组的有65人,那么六年级参加课外兴趣小组的同学共有( )人。
18.2022年第一季度,包河区实现地区生产总值(又称GDP)33830000000元,总量城区第一,横线上的数读作( ),改写成以“亿”作单位的数是( )亿。
19.用一根48分米的铁丝做一个长方体框架,使它的长、宽、高的比是5∶4∶3,在这个长方体框架外面糊一层纸,至少需要( )平方分米的纸。它的体积是( )立方分米。
20.2024年“五一”假日期间,溧水共接待游客799500人次,同比增长27.9%,将横线上的数改写成用“万”作单位的数是( )万人;实现旅游收入679000000元,同比增长4.14%,将横线上的数省略“亿”后面的尾数约是( )亿元。
21.观察下列等式,你会发现一些规律,依照你发现的规律,请在最后一个等式的括号里填上相同的数。
3+1=3×1,2+1=2×1,1+3=1×3,…,1+( )=1×( )。
22.三条边长分别是6厘米、8厘米、10厘米的直角三角形,将它的最短边对折与斜边相重合(如下图),那么,图中阴影部分面积是( )平方厘米。
23.中的“5”表示5个( ),8.006中的“6”表示6个( )。
24.如图,用边长1厘米的小正方形像上面这样拼摆。照这样摆下去,第6个图形的面积是( )平方厘米,第n个图形的周长是( )厘米。
25.6.4957用四舍五入法保留两位小数约是( ),保留三位小数约是( )。
26.将改写成数值比例尺是( )∶( );在一幅以它做比例尺的地图上,图上距离和实际距离成( )比例。
27.一个圆柱体的底面直径和高都是2厘米,它的侧面积是( )平方厘米,表面积是( )平方厘米,体积是( )立方厘米。
28.将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的体积最大是 立方厘米。
29.陈明用圆规和直尺画半圆,他将圆规两脚间的距离定为4厘米,画出的半圆的周长是( )厘米。
30.30比( )少40%,20比15多。
31.0.875=( )∶4=÷( )=( )%。
32.阳光小学组织安全意识知识竞赛,共20题。评分规则是答对一题得10分,答错一题扣5分,弃权不扣也不加。芳芳小组弃权两道,得了120分,他们答对了( )题。
33.把一根4米长的钢管平均锯成5段,每段是全长的,每段长( )米。
34.在50以内,6和8的公倍数有 ;9和27的最大公因数是 。
35.如图的国际象棋棋盘上,白棋“”的位置可以记录为“e4”,它向上走一格,可以记录为e4~e5。黑棋“”先向右走5格,再向下走2格,可以记录为 ~ 。
36.李叔叔在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图,其中黄瓜的种植面积是80平方米,萝卜的种植面积是( )平方米,番茄比黄瓜多种植( )%。
37.一根1米长的圆柱体钢材,截去2分米的一段后,表面积减少了25.12平方分米,原来这根钢材的体积是( )立方分米。
38.0.8==( )∶20=32( )=( )%。
39.六年级一班图书角放着一些课外书,书的本数在110~130本之间,其中是科技类书籍,是文学类书籍,这个班图书角里有( )本科技类书籍。
40.如图,底面半径为0.5米的油桶,在两侧墙内滚动,两墙之间的距离为51.24米,油桶从墙的一侧滚到另一侧要滚( )圈。
41.每个篮球a元,比每个足球便宜10元。篮球和足球各买一个,共需 元。
42.小明有一个奇怪的时钟,分针的速度是时针的3倍,秒针速度最快,每10分钟秒针追上时针一次,每20分钟秒针追上分针一次,那么秒针 分钟走完一圈。
43.3÷10=9∶( )( )÷120=( )%。
44.三角形的面积和平行四边形的面积相等,底也相等。平行四边形的高是6分米,三角形的高是( )分米。
45.有96名少年队员在一次夏令营活动中要过一条小河去爬山。现在只有一条可乘6人的橡皮艇(包括划船的同学),过一次河需要2分钟。全体队员渡到河对岸至少需要 分钟。
46.一个三位数既是2的倍数,又是3的倍数,而且又有因数5,这个三位数最大是( ),把它分解质因数是( )。
47.∶化成最简单的整数比是( ),比值是( )。
48.某小区连续三天举办公益活动,第1天来了190人,第2天来了130人,第3天来了180人,前两天都参加的有30人,后两天都参加的有40人,那么一共至少有 人来参加公益活动。
49.写出16的所有因数:( ),选择其中的四个数组成一个比例( )。
50.据统计,截至北京时间6月16日24时,全球新冠肺炎确诊病例上升至537530094例,这个数读作( ),保留一位小数大约是( )亿。
51.将班上的47名同学按照、、、、、、、、、、、、、……的顺序贴上标签,则最后一名学生的标签为 。
52.人体正常体温(腋下温度)平均为,如果我们把体温标准定在,可记作,那么35.7℃可以记作 ℃,37.3℃可以记作 ℃。
53.( )分=1.5时 0.75平方千米=( )公顷
54.习近平总书记在全国教育大会上提出教育要“五育并举”,阳光小学开展了丰富多彩的“劳动教育”实践活动。下图是该校六年级学生参加“劳动教育”实践活动情况的统计图,参加烹饪小组的人数占总人数的( )%,如果六年级参加“劳动教育”实践活动的一共有120人,那么参加手工小组的有( )人。
55.渔船在海上遇险,向救援中心发送遇险位置的求救信号应该是:渔船在海鸟岛的( )偏( )( )°方向( )千米处。
56.( )∶20==( )÷36==( )%=( )折。
57.两根长短粗细不同的蜡烛,短的可燃8小时,长的可燃的时间是短的,同时点燃两根蜡烛,经过3小时,它们长短正好相等,未点燃之前,短蜡烛比长蜡烛短( )。
58.如图,把打乱的积木拼图还原,要把1号积木向右平移( )格,把2号积木绕点A逆时针旋转( )°。
59.如图,将一个高6厘米的圆柱转化成长方体,表面积增加了48平方厘米,这个圆柱的底面半径是( )厘米。
60.小静打开数学书时,发现两页页码之积是420,这两页分别是( )页和( )页。
《小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学苏教版》参考答案
1.4;15;;125
【分析】小数化成分数,两位小数先化成分母为100的分数,再化简成最简分数;
分数与比的关系:分子相当于比的前项,分母相当于比的后项,分数线相当于比号;
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号。
【详解】1.25==
=5∶4
==
1.25=125%
即5∶4===125%=1.25。
(第三个空答案不唯一)
【点睛】掌握小数、分数、百分数的互化、分数的基本性质、分数与比的关系是解题的关键。
2.56.52
【分析】这个圆锥的底面直径是6分米,高是6分米,再根据圆锥的体积=底面积×高÷3,解答即可。
【详解】6÷2=3(分米)
3.14×3×3×6÷3
=9.42×3×6÷3
=28.26×6÷3
=169.56÷3
=56.52(立方分米)
这个圆锥的体积是56.52立方分米。
【点睛】熟练掌握圆锥的体积公式,是解答此题的关键。
3.150
【分析】先计算出第一天看书的页数,用第一天看书的页数除以20%,即为这本书的总页数,据此解答。
【详解】(54-24)÷20%
=30÷20%
=150(页)
【点睛】解答本题的关键是明确已知一个数的百分之几是多少,求这个数,用除法计算。
4.见详解
【分析】等腰三角形的两条腰相等。从图中可知,OA和OB都是圆的半径,那么OA=OB,据此判断三角形AOB是等腰三角形。
【详解】图中三角形AOB一定是等腰三角形,作出这个判断的依据是OA和OB都是圆的半径,同一个圆的半径相等。
5. 一亿八千一百三十四万四千 18134.4
【分析】根据整数的读法:从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位有一个或连续几个0,都只读一个零,据此读出此数;
改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字。
【详解】181344000读作:一亿八千一百三十四万四千
181344000=18134.4万
太平洋是世界上最大、最深的海洋,总面积为181344000平方千米,横线上的数读作:一亿八千一百三十四万四千;改写成用“万”作单位的数是18134.4万平方千米。
6. 3 50 0.35/
【分析】根据1升=1000毫升,1平方千米=100公顷,高级单位转化为低级单位乘进率,低级单位转化为高级单位除以进率,单名数换复名数,整数部分填在高级单位中,小数部分乘进率转化为低级单位,据此解答。
【详解】(1)3.05升=3升+0.05升
0.05×1000=50(毫升)
3.05升=3升50毫升
(2)35÷100=0.35(平方千米)
35公顷=0.35平方千米
7. 5m 30
【分析】根据求一个数的几倍是多少,用这个数乘倍数,据此用m×4求出学校合唱队女生有多少人,再加上男生人数就是合唱队一共有多少人;把男生人数代入上一步求出的关系式进行计算即可。
【详解】4×m=4m(人)
4m+m=5m(人)
当m=6时,
5m=5×6=30(人)
所以学校合唱队一共有5m人;如果男生有6人,则学校合唱队一共有30人。
8. 5 6
【分析】根据比例的基本性质:两内项之积等于两外项之积,写出这个比例式;化简,即可解答。
【详解】x=y,
x∶y=∶
=(×15)∶(×15)
=10∶12
=(10÷2)∶(12÷2)
=5∶6
【点睛】利用比例的基本性质以及比的基本性质进行解答。
9.
【分析】根据求一个数占另一个数的几分之几,用除法计算,用现在快速对接时间除以原来对接时间,得数用分数表示,能约分的要约为最简分数。
【详解】
勤劳智慧的中国人“可上九天揽月,可下五洋捉鳖”。自2011年首次实现“神舟号”飞船与“天宫号”空间站交会对接以来,我国的交会对接技术经历了从44小时到约6小时快速对接的跨越,创造了世界纪录。现在快速对接时间约占原来对接时间的。
10.15;6;36;75
【分析】被除数=除数×商,8×0.75=6;根据小数化分数的方法,0.75=,根据分数与比的关系,比的基本性质,=3∶4=(3×5)∶(4×5)=15∶20;根据分数的基本性质,==;根据小数化百分数的方法,0.75=75%。
【详解】根据分析可得:
15∶20=0.75=6÷8==75%
【点睛】考查了小数、分数、百分数的转化方法、比的基本性质、分数的基本性质,学生应掌握。
11.36
【分析】圆柱形钢材沿横截面截成三段后,表面积比原来增加了4个横截面面积。已知表面积比原来增加了9.6平方分米,用9.6除以4即可求出圆柱的横截面面积。圆柱的体积=底面积×高,用这根钢材的横截面面积乘长即是钢材的体积。
【详解】1.5米=15分米
9.6÷4×15
=2.4×15
=36(立方分米)
【点睛】本题考查立体图形的切拼和圆柱体积的应用。明确圆柱表面积比原来增加了4个横截面面积,继而求出横截面的面积是解题的关键。
12.5
【分析】根据题意,利用糖水的质量×含糖率即可求出糖的质量,糖水里又放入一些糖和5克热水,所以糖水的质量要增加,利用含糖率=糖的质量÷糖水的质量×100%,列方程解答即可。
【详解】解:设陈老师又放入x克糖。
40×10%=4(克)
(4+x)÷(40+x+5)×100%=18%
400+100x=720+18x+90
82x=810-400
82x=410
x=5
【点睛】此题属于百分率实际应用,计算的结果最大值为100%,都是用一部分数量(或全部数量)除以全部数量乘百分之百。
13.1.06
【分析】根据百分数乘法的意义,可知调整前100万元收取(100×2%)万元;调整后20万元部分收取(20×1.2%)万元,20万元到50万元部分收取[(50-20)×1%]万元,50万元到100万元部分收取[(100-50)×0.8%]万元,然后将三部分相加,即可求出调整后,一共收取的公证费;然后用调整后的公证费减去调整前的公证费,即可求出节省的钱数。
【详解】100×2%=2(万元)
20×1.2%+(50-20)×1%+(100-50)×0.8%
=20×1.2%+30×1%+50×0.8%
=0.24+0.3+0.4
=0.94(万元)
2-0.94=1.06(万元)
继承一套总价值为100万元的房屋至少能省1.06万元。
14.30;70;七;35
【分析】根据比与分数的关系7∶10=,根据分数的基本性质,分子、分母都乘3就是;
同理,的分子、分母都乘10就是,改写成百分数是70%;
根据折扣的意义70%就是七折;
根据比与除法的关系7∶10=7÷10,再根据商不变的性质被除数、除数都乘5就是35÷50。
【详解】
=70%=7∶10=七折=35÷50
15.(1) 5 17;
(2) 2023 2025
【分析】观察所给算式1×3+1=22,2×4+1=32,3×5+1=42。对于乘法部分,第一个因数依次是1、2、3,呈现依次增加1的规律;第二个因数依次是3、4、5,比对应的第一个因数大2。等式右边是一个数的平方,这个数比乘法算式中的第一个因数大1。总结规律为:n×(n+2)+1=(n+1)2(n为自然数)然后根据此规律计算填空。
【详解】(1)4×6+1:这里n=4,根据规律(n+1)2,即4+1=5,所以4×6+1=52,16×18+1:这里n=16,16+1=17,所以16×18+1=172
4×6+1=52,16×18+1=172
(2)因为结果是20242,由规律(n+1)2=20242,可得n+1=2024,则n=2023,n+2=2023+2=2025,即2023×2025+1=20242
2023×2025+1=20242。
16.720
【分析】由图①可得,880mL=原来水640mL+圆柱的体积,因此用880-640即可求出圆柱的体积。等底等高的圆柱的体积是圆锥体积的3倍,据此用圆柱的体积除以3,求出圆锥的体积,最后用量杯原来的水的体积加圆锥的体积,可得出图②量杯水面刻度。
【详解】(880-640)÷3+640
=240÷3+640
=80+640
=720(mL)
所以图②中圆锥放入后量杯水面刻度显示应是720mL。
17.(1)22
(2)250
【分析】(1)把六年级参加各兴趣小组的人数看作单位“1”,用单位“1”减去参加体育、美术、音乐兴趣小组人数所占的百分率就是参加其它兴趣小组人数所占的百分率;
(2)根据除法的意义,用参加美术小组的人数除以所占的百分率就是六年级参加课外兴趣小组同学的总人数。
【详解】(1)1-34%-26%-18%
=66%-26%-18%
=40%-18%
=22%
参加其他兴趣小组的同学占六年级学生总数的22%。
(2)65÷26%=250(人)
六年级参加课外兴趣小组的同学共有250人。
18. 三百三十八亿三千万 338.3
【分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位一个0或连续几个0都只读一个零,即可读出此数;
改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“亿”字。
【详解】33830000000读作:三百三十八亿三千万
33830000000=338.3亿
【点睛】本题主要考查整数的读法和改写,分级读即可快速、正确地读出此数,改写时要注意带计数单位。
19. 94 60
【分析】长方体的棱长和=(长+宽+高)×4,据此用长方体的棱长和除以4,求出长、宽、高的和,把长、宽、高的比看作份数比,用长、宽、高的和除以份数和,求出1份是多少分米,再分别乘长、宽、高各自的份数,求出长、宽、高分别是多少分米,再根据长方体的表面积=(长×宽+宽×高+长×高)×2,长方体的体积=长×宽×高,代入数据解答即可。
【详解】长、宽、高的和:
48÷4=12(分米)
总份数:
5+4+3=12(份)
12×=5(分米)
12×=4(分米)
12×=3(分米)
表面积:
(5×4+4×3+5×3)×2
=(20+12+15)×2
=47×2
=94(平方分米)
体积:5×4×3
=20×3
=60(立方分米)
故至少需要94平方分米的纸,它的体积是60立方分米。
20. 79.95 7
【分析】改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;
省略“亿”后面的尾数求它的近似数,要把亿位的下一位千万位上的数进行四舍五入,再在数的后面写上“亿”字。
【详解】799500=79.95万
679000000≈7亿
2024年“五一”假日期间,溧水共接待游客799500人次,同比增长27.9%,将横线上的数改写成用“万”作单位的数是79.95万人;实现旅游收入679000000元,同比增长4.14%,将横线上的数省略“亿”后面的尾数约是7亿元。
21. 2 2
【分析】先把带分数化成假分数,再找规律,即+=,,,观察可知两个分数的分子相同,且是两个分母的和,根据此规律可求解。
【详解】+=,,,观察可知两个分数的分子相同,且是两个分母的和,所以,即1+2=1×2,
【点睛】本题主要考查“式”的规律,先变化原式,再发现规律,根据规律解答。
22.6
【分析】如图:根据题意得BD=BC=6厘米,AD=AB-BD=10-6=4厘米,因为三角形ADE的面积=×AD×DE,三角形BDE的面积=×BD×DE,所以三角形ADE的面积∶三角形BDE的面积=AD∶BD=4∶6=2∶3,又因为三角形ABC的面积=×6×8=24(平方厘米),所以三角形ADE的面积==6(平方厘米)。
【详解】根据分析得,BD=6(厘米)
AD=10-6=4(厘米)
三角形ADE的面积∶三角形BDE的面积∶三角形BCE=AD∶BD∶BC=4∶6∶6=2∶3∶3
三角形ABC的面积=×6×8=24(平方厘米)
三角形ADE的面积==6(平方厘米)
【点睛】此题主要考查等底等高的三角形面积相等,关键是找准面积的比。
23. 千分之一
【分析】根据分数的意义及每个数位上的数代表不同的计数单位,据此解答。
【详解】中的“5”表示5个,8.006中的“6”表示6个千分之一。
【点睛】本题主要考查了分数的意义及小数计数单位的认识。
24. 21 4n
【分析】观察可得规律:第1个图形面积是1平方厘米,第2个图形面积是(1+2)平方厘米,第3个图形面积是(1+2+3)平方厘米……,第n个图形面积是(1+2+3+…+n)平方厘米,据此得出第6个图形的面积。
第1个图形周长是4厘米,第2个图形周长是8厘米,第3个图形周长是12厘米……,据此得出第n个图形的周长。
【详解】第6个图形的面积是:1+2+3+4+5+6=21(平方厘米)
第1个图形的周长是:4×1=4(厘米)
第2个图形的周长是:4×2=8(厘米)
第3个图形的周长是:4×3=12(厘米)
……
第n个图形的周长是:4×n=4n(厘米)
因此第6个图形的面积是21平方厘米,第n个图形的周长是4n厘米。
25. 6.50 6.496
【分析】保留两位小数看千分位,保留三位小数看万分位,小于5直接舍去,大于或等于5向前一位进一,据此保留近似数。
【详解】
6.4957用四舍五入法保留两位小数约是6.50,保留三位小数约是6.496。
26. 1 2000000 正
【分析】由线段比例尺可知,图上距离1厘米相当于实际距离20千米,根据“图上距离∶实际距离=比例尺”改写成数值比例尺,注意单位的换算:1千米=100000厘米。
判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】改写成数值比例尺是:
1厘米∶20千米
=1厘米∶(20×100000)厘米
=1∶2000000
因为图上距离∶实际距离=比例尺(一定),比值一定,所以图上距离和实际距离成正比例。
【点睛】本题考查线段比例尺和数值比例尺的转化,正、反比例的意义及辨识方法,掌握图上距离、实际距离、比例尺之间的关系是解题的关键。
27. 4π 6π 2π
【分析】根据圆柱的表面积公式S表=S侧+2S底,其中S侧=πdh,S底=πr2;根据圆柱的体积公式V=Sh,代入数据计算即可。
【详解】圆柱的侧面积:
π×2×2=4π(平方厘米)
圆柱的底面积:
π×(2÷2)2=π(平方厘米)
圆柱的表面积:
4π+2π=6π(平方厘米)
圆柱的体积:
π×2=2π(立方厘米)
【点睛】掌握圆柱的侧面积、表面积、体积计算公式是解题的关键。
28.150.72
【分析】(1)以4厘米的边为轴旋转时,它的底面半径是3厘米,高是4厘米,再根据圆柱的体积公式可求出它的体积;
(2)以3厘米的边为轴旋转时,它的底面半径是4厘米,高是3厘米,再根据圆柱的体积公式可求出它的体积。
再比较大小即可求解。
【详解】(1)以4厘米的边为轴旋转时,它的体积是:
3.14×32×4
=3.14×9×4
=113.04(立方厘米)
(2)以3厘米的边为轴旋转时,它的体积是:
3.14×42×3
=3.14×16×3
=150.72(立方厘米)
150.72>113.04
将一张长4厘米、宽3厘米的长方形纸以一条边为轴旋转一周,得到一个圆柱,这个圆柱的最大体积是150.72立方厘米。
29.20.56
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径的长度,根据半圆的周长公式:C=πr+2r,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
【点睛】此题主要考查半圆周长公式的灵活运用,关键是熟记公式。
30.50;
【分析】(1)把要求的数看作单位“1”,30相当于要求数的(1-40%),根据已知一个数的百分之几是多少,求这个数,用除法解答;
(2)把15看作单位“1”,先求出20比15多多少,再根据求一个数是另一个数的几分之几,用除法解答。
【详解】(1)30÷(1-40%)
=30÷0.6
=50
30比50少40%。
(2)(20-15)÷15
=5÷15
=
20比15多。
【点睛】此题考查的目的是理解掌握分数、百分数的乘法、除法的计算法则,并且能够正确熟练地进行计算。
31.3.5;24;;87.5%
【分析】0.875化成分数化简后就是;根据分数的基本性质,的分子、分母同时乘4就是,32-8=24;根据除法各部分之间的关系,除数=被除数÷商,÷=;根据比值=比的前项÷比的后项,即比的前项=比值×比的后项,0.875×4=3.5;0.875的小数点向右移动两位,同时添上百分号可化成87.5%。
【详解】0.875=3.5∶4=÷=87.5%
【点睛】此题考查小数、分数、百分数、比和除法之间的转化,根据它们之间的关系和性质进行转化。
32.14
【分析】根据“每做对一道得10分,答错扣5分,”可知:答错一题比答对一题少得10+5=15分;假设芳芳小组全部答对得分是10×18=180(分),比120分多得180-120=60(分),那么他们答错了:60÷(10+5)=4(道);所以芳芳小组答对:18-4=14道题。
【详解】[10×(20-2)-120]÷(10+5)
=[10×18-120]÷15
=[180-120]÷15
=60÷15
=4(道)
20-2-4
=18-4
=14(道)
【点睛】鸡兔同笼问题一般利用解设法解答,本题先假设全部答对,得出与实际得分的差就是每道错题对应的失分,从而求出错题数。
33.;
【分析】求每段是全长的几分之几,就是将这段钢管长看作单位“1”,平均分成5份,表示其中的一份;求每段长多少米,就是将4米平均分成5段,求一段长多少米,据此解答。
【详解】1÷5
4÷5(米)
把一根4米长的钢管平均锯成5段,每段是全长的,每段长米。
34. 24、48 9
【分析】公倍数是两个数公有的倍数,先找出两个数的倍数,从中找出公有的倍数;
公因数是两个数公有的因数,先求出两个数的因数,然后找出公有的因数即可,公因数中最大的一个就是这两个数的最大公因数,据此找出9和27的最大公因数。
【详解】(1)50以内6和8的倍数是:
6的倍数是:6、12、18、24、30、36、42、48,
8的倍数是:8、16、24、32、40、48,
50以内6和8的公倍数有:24、48;
(2)9的因数有:1、3、9,
27的因数有:1、3、9、27,
9和27的公因数有:1、3、9;9和27的公因数1、3、9中,9是最大的,所以9和27的最大公因数是9。
【点睛】此题需要学生掌握倍数、公倍数、因数、公因数和最大公因数的意义和求法。
35. b7 g5
【分析】由题意得,位置的记法是“先列后排”,黑棋“”先向右走5格,再向下走2格,本来在b7的位置,现在到了g5的位置,据此解答即可。
【详解】黑棋“”先向右走5格,再向下走2格,可以记录为b7~g5。
【点睛】此题考查了用数对表示位置在实际当中的运用。明确棋子前后位置的数对是解题的关键。
36. 96 75
【分析】以这块地的面积为单位“1”,已知黄瓜的种植面积是80平方米,占这块地的面积的20%,根据已知一个数的百分之几是多少,求这个数用除法计算,求出这块地的面积。
萝卜的种植面积占这块地的(1-35%-20%-21%),根据求出一个数的几分之几是多少,用乘法计算,用这块地的面积×(1-35%-20%-21%),求出萝卜的种植面积。
已知番茄种植面积占这块地的35%,用这块地的面积×35%,求出番茄的种植面积。根据求一个数比另一个数多百分之几,用除法计算,以黄瓜的种植面积为单位“1”,用番茄比黄瓜多种植的面积÷黄瓜的种植面积即可求出番茄比黄瓜多种植百分之几。
【详解】80÷20%=400(平方米)
400×(1-35%-20%-21%)
=400×24%
=96(平方米)
400×35%=140(平方米)
(140-80)÷80
=60÷80
=0.75
=75%
因此,萝卜的种植面积是96平方米,番茄比黄瓜多种植75%。
37.125.6
【分析】截去2分米的一段后,表面积减少的部分正好是这段2分米钢材的侧面积,用侧面积除以高,求出底面圆的周长,利用圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,求出底面半径,再根据圆柱的体积公式:体积=底面积×高,计算出体积。
【详解】1米=10分米
25.12÷2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(分米)
3.14×22×10
=3.14×4×10
=12.56×10
=125.6(立方米)
一根1米长的圆柱体钢材,截去2分米的一段后,表面积减少了25.12平分方米,原来这根钢材的体积是125.6立方米。
【点睛】本题考查圆柱表面积及体积的计算方法,根据表面积减少情况计算出原钢材的底面半径,再结合钢材的长进一步计算出体积,注意单位名数的换算。
38.5;16;40;80
【分析】先把0.8化成分数,0.8==;根据分数与比的关系、分数的基本性质,把的分子和分母同时乘4,得==16∶20;根据分数与除法的关系,把的分子和分母同时乘8,得==32÷40;把0.8的小数点向右移动两位,化成百分数为80%。
【详解】0.8==16∶20=32÷40=80%。
【点睛】本题考查了分数、小数和百分数的互化,分数与除法、比的关系,分数的基本性质等,要牢固掌握相关知识并熟练运用。
39.30
【分析】根据题意,图书角书的数量必须能平均分成4和5份,也就是书的本数必须是4和5的倍数,找出在110到130之间4和5的公倍数即可求出总本数,再乘,即可求出这个班图书角里有多少本科技类书籍。
【详解】4×5=20
20×6=120(本)
120×=30(本)
这个班图书角里有30本科技类书籍。
【点睛】本题考查公倍数的计算及分数乘法的计算和应用。理解题意,找出数量关系,列式计算即可。
40.16
【分析】油桶每滚一圈经过的距离也就是圆形油桶的周长,根据圆的周长=2πr,代入数值计算出油桶滚一圈经过的距离;其中油桶滚动的距离=两墙之间的距离-油桶底面的直径,最后用油桶滚动的距离除以圆的周长,所得结果即为油桶要滚的圈数。
【详解】(51.24-0.5×2)÷(2×3.14×0.5)
=(51.24-1)÷3.14
=50.24÷3.14
=16(圈)
因此油桶从墙的一侧滚到另一侧要滚16圈。
41.(2a+10)/(10+2a)
【分析】每个篮球a元,比每个足球便宜10元。每个足球是(10+a)元,篮球和足球各买一个,共需多少元,用加法列式并化简即可解答。
【详解】a+(10+a)=2a+10(元)或10+2a(元)
每个篮球a元,比每个足球便宜10元。篮球和足球各买一个,共需(2a+10)或(10+2a)元。
42.
8
【分析】根据题意可以设时针速度为度/分钟,分针速度为 度/分钟,秒针速度为 度/分钟。
根据秒针每10分钟追上时针一次,也就是当秒针和时针在同一地点出发时,秒针的速度快,时针的速度慢,当秒针追上时针时,秒针比时针都走一圈,也就是360°,即得方程:;
同理每20分钟追上分针一次,得方程:。联立方程解得,秒针一圈是360°,则除以秒针的速度就是秒针的时间。
【详解】解:设时针速度为度/分钟,则分针速度为度/分钟,秒针速度为度/分钟。
秒针追上时针:
①
秒针追上分针:
②
将①式和②式相减
代入①得:
(分钟)
则秒针8分钟走完一圈。
【点睛】找到秒针、分针、时针三者之间的数量关系式,联立两个方程找出秒针的速度,最后得出时间。
43.30;50;36;30
【分析】根据比与除法的关系3÷10=3∶10,再根据比的性质比的前、后项都乘3就是9∶30;根据分数与除法的关系3÷10,再根据分数的基本性质,分子、分母都乘5就是;根据商不变的性质,3÷10的被除数、除数都乘12就是36÷120;3÷10=0.3,把0.3的小数点向右移动两位添上百分号就是30%。
【详解】3÷10=3∶10=(3×3)∶(10×3)=9∶30
3÷10=
因此,3÷10=9:3036÷120=30%。
44.12
【分析】等面积等底的平行四边形和三角形,三角形的高是平行四边形高的2倍,直接用平行四边形的高×2=三角形的高,据此列式计算。
【详解】6×2=12(分米)
三角形的高是12分米。
45.74
【分析】要想过河所用时间最少,则每次尽可能坐满,派出一个同学来划船,则每次剩下5个位置,95÷5即可求出有几个5,也就是需要送几次,也就是19次,而划船的同学需要返回18次,所以船一共来回了(19+18)次,每次需要2分钟,用(19+18)×2即可求出全部人过河至少需要的时间。
【详解】96-1=95(人)
95÷5=19(次)
19+18=37(次)
37×2=74(分钟)
全体队员渡到河对岸至少需要74分钟。
【点睛】解此题关键是理解渡船就要有一个撑船的,实际上除最后一次,每次只能坐5人。
46. 990 990=2×3×3×5×11
【分析】同时是2、3和5的倍数的特征是,个位上必须是0,且各位上的数字之和是3的倍数;据此解答。
【详解】一个三位数既是2的倍数,又是3的倍数,而且又有因数5,这个三位数最大是990,
把990分解质因数:
990=2×3×3×5×11。
【点睛】此题考查的目的是理解掌握同时是2、3和5的倍数的特征,以及分解质因数的方法。
47. 9∶1 9
【分析】根据比的基本性质作答,即比的前项和后项同时乘或除以一个数(0除外),比值不变,和分母的最小公倍数是15,比的前项和后项同时乘15,将其化成最简的整数比9∶1;求比值是用比的前项除以比的后项所得的数值,也可以用最简比的前项除以后项即可得比值。
【详解】∶
=(×15)∶(×15)
=9∶1
∶===9
或9∶1=9÷1=9
所以,∶化成最简单的整数比是9∶1,比值是9。
48.
430
【分析】为了使总人数最少,应尽可能让重复参加的人数最多。
已知前两天都参加的有30人,后两天都参加的有40人。
假设三天都参加的人数最多为30人(即前两天重叠的30人全部参加了第三天),则后两天重叠的40人中,有30人三天都参加,剩余10人只参加后两天。
即第一天:190人,其中30人三天都参加,剩余160人只参加第一天。
第二天:130人,其中30人三天都参加,10人只参加后两天,剩余90人只参加第二天。
第三天:180人,其中30人三天都参加,10人只参加后两天,剩余140人只参加第三天。
通过分解各天人数并计算不重复部分,即可得到总人数。
【详解】190-30=160(人)
130-30-10=90(人)
180-30-10=140(人)
160 +90 +140 +30+10 =430(人)
则一共至少有430人来参加公益活动。
【点睛】总数最少就是让重复参加的人最多,重复参加最多的有30人,分别在求出三天只参加的人数,再加上重复的人数即可得出最少情况下的人数。
49. 1,2,4,8,16 1∶2=4∶8
【分析】找一个数的因数的方法:列乘法算式找因数,按照从小到大的顺序,一组一组地写出所有积是这个数的乘法算式,乘法算式中的两个因数就是这个数的因数。
表示两个比相等的式子叫做比例。根据比例的意义,从16的因数中选择四个数,分别求出两个数的比值,比值相等的能组成比例;反之,比值不相等的,就不能组成比例。
【详解】16=1×16=2×8=4×4,所以16的因数有:1,2,4,8,16;
1∶2=1÷2=0.5
4∶8=4÷8=0.5
比值相等,所以1,2,4,8可以组成一个比例,如:1∶2=4∶8。
填空如下:
写出16的所有因数:(1,2,4,8,16),选择其中的四个数组成一个比例(1∶2=4∶8)。(最后一个空答案不唯一)
50. 五亿三千七百五十三万零九十四 5.4
【分析】从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续几个0都只读一个零,即可读出此数;改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,再用“四舍五入”法保留一位小数,最后在数的后面写上“亿”字。
【详解】537530094读作:五亿三千七百五十三万零九十四;
保留一位小数大约是:537530094=5.37530049亿≈5.4亿。
【点睛】本题主要考查多位数的读法和求近似数,读数时要注意零的读法,求近似数时要注意带计数单位。
51.B
【分析】通过观察发现,是按照A、B、C、D、A这样的方式每5个循环的。利用除法,即可求出47名学生里面有9个这样的循环剩下的2个人分别是A和B。
【详解】47÷5=9(组)……2(人)
则最后一名学生的标签为B。
52. ﹣0.8 ﹢0.8/0.8
【分析】正负数表示一组相反意义的量,根据题意,比36.5℃高的部分记作正数,在数字前加上“﹢”号,也可不加。比36.5℃低的部分记作负数,在数字前加上“﹣”号。据此解答。
【详解】36.5℃-35.7℃=0.8℃
37.3℃-36.5℃=0.8℃
人体正常体温(腋下温度)平均为,如果我们把体温标准定在,可记作,那么35.7℃可以记作﹣0.8℃,37.3℃可以记作﹢0.8℃(或0.8℃)。
53. 90 75
【分析】高级单位时化低级单位分乘进率60。
高级单位平方千米化低级单位公顷乘进率100。
【详解】90分=1.5时
0.75平方千米=75公顷
【点睛】此题是考查时间的单位换算、面积的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
54. 45 30
【分析】把参加“劳动教育”实践活动总人数看作单位“1”;
观察扇形统计图可知,参加手工小组的人数总人数的四分之一;所以手工小组的人数占参加“劳动教育”实践活动总人数的25%;
求参加烹饪小组人数占总人数的百分之几,用1减去参加种植小组占总人数的百分率,减去参加烹饪小组人数占总人数的百分率,即可解答;
用六年级参加“劳动教育”实践活动的总人数乘参加手工小组占总人数的百分率,即可解答。
【详解】1-30%-25%
=70%-25%
=45%
120×25%=30(人)
【点睛】根据扇形统计图提供的信息,以及求一个数的百分之几是多少的知识进行解答。
55. 北/东 东/北 30/60 62.5
【分析】(1)(2)(3)确定方向:以海岛为观测点,根据图中“北”的标识确定方向。方向描述有两种方式,一种是北偏东,用量角器测量渔船与正北方向夹角为30°,即北偏东30°;另一种是东偏北,此时渔船与正东方向夹角为60°,即东偏北60°。
(4)计算距离:已知图中比例尺为1∶2500000,意味着图上1厘米代表实际距离2500000厘米,也就是25千米。测量图上渔船到海岛的距离(假设测量后经计算对应实际距离为62.5千米,可根据比例尺进行换算得到实际距离。
【详解】(1)(2)(3)北偏东30°情况:用量角器测量得出渔船在海岛的北偏东30°方向。(4)因为比例尺1∶2500000,量得图上渔船到海岛距离为2.5厘米,实际距离为2.5×25=62.5千米。
渔船在海鸟岛的北偏东30°方向62.5千米处。
东偏北60°情况:用量角器测量得出渔船在海岛的东偏北60°方向。因为比例尺1∶2500000,量得图上渔船到海岛距离为2.5厘米,实际距离为2.5×25=62.5千米。
渔船在海鸟岛的东偏北30°方向62.5千米处。(答案不唯一)
56.15;27;9;75;七五
【分析】根据比与分数的关系=3∶4,再根据比的基本性质比的前、后项都乘5就是15∶20;根据分数与除法的关系=3÷4,再根据商不变的性质被除数、除数都乘9就是27∶36;根据分数的基本性质的分子、分母都乘3就是;3÷4=0.75,把0.75的小数点向右移动两位添上百分号就是75%;根据折扣的意义75%就是七五折。
【详解】=3∶4=(3×5)∶(4×5)=15∶20
=3÷4=(3×9)÷(4×9)=27÷36
=
=3÷4=0.75=75%
75%=七五折
15∶20==27÷36==75%=七五折
57.
【分析】短的可燃8小时,长的可燃的时间是短的,长的可燃烧的时间是8×=4小时;燃烧3小时,短蜡烛燃烧了,长蜡烛燃烧了;短蜡烛还剩1-没有燃烧,长蜡烛还有1-没有燃烧,剩下的部分相等,即短蜡烛的(1-)=长蜡烛的(1-),即短蜡烛×(1-)=长蜡烛×(1-),再根据比例的基本性质:比例的两个内项之积等于两个外项之积,据此根据比例基本性质的逆运算,求出短蜡烛与长蜡烛的比,即求出短蜡烛是长蜡烛的几分之几,设长蜡烛长是1,求出短蜡烛,再用长蜡烛与短蜡烛的差,除以长蜡烛,即可解答。
【详解】长的蜡烛燃烧时间:8×=4(小时)
3小时短蜡烛燃烧了3÷8=,还剩1-=;
3小时长蜡烛燃烧了3÷4=,还剩1-=。
短蜡烛×=长蜡烛×
短蜡烛∶长蜡烛=∶
=(×8)∶(×8)
=2∶5
即短蜡烛是长蜡烛的。
设长蜡烛长度是1。
(1-)÷1
=÷1
=
两根长短粗细不同的蜡烛,短的可燃8小时,长的可燃的时间是短的,同时点燃两根蜡烛,经过3小时,它们长短正好相等,未点燃之前,短蜡烛比长蜡烛短。
58. 2/两 90
【分析】平移是指在平面内,将一个图形沿着某个方向移动一定的距离,这样的运动叫做图形的平移。
旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
【详解】
如图,把打乱的积木拼图还原,要把1号积木向右平移(2)格,把2号积木绕点A逆时针旋转(90)°。
59.4
【分析】将一个圆柱切拼成一个长方体,形状变了,体积不变。长方体的长相当于圆柱底面周长的一半,宽相当于圆柱的半径,高相当于圆柱的高。长方体的上下面等于圆柱的上下底面,长方体的前后面等于圆柱的侧面,表面积增加了左右面积,即增加的面积=宽×高×2=半径×高×2=48平方厘米。已知高是6厘米,据此求出半径即可。
【详解】48÷2÷6
=24÷6
=4(厘米)
这个圆柱的底面半径是4厘米。
60. 20 21
【分析】根据题意,两页页码之积是420,先把420分解质因数,再把这些质因数重新组合,变成连续两个自然数相乘的形式,即可得解。
【详解】420=2×2×3×5×7=(2×2×5)×(3×7)=20×21
这两页分别是20页和21页。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
