小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学西师大版
文档属性
| 名称 | 小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学西师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 484.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-15 20:02:24 | ||
图片预览




文档简介
小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学西师大版
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.百分之三十二写作 ;45%读作: 。
2.如图中圆的周长是20厘米,且圆的面积与长方形的面积相等,那么阴影部分的周长是( )厘米。
3.比45千克重是( )千克;( )千克比45千克轻千克。
4.如图,已知长方形为8厘米,宽为4厘米,则图中阴影部分的面积为( )。
5.如图中平行四边形的面积是( )cm2。另一条底边长是6cm,它对应的高是( )cm。(保留一位小数)
6.如图所示,把一个三角形平均分成两个小三角形,每个小三角形的内角和是( )°。
7.( )∶20=9÷( )=0.6==( )%。
8.买一副羽毛球拍需要a元,买一副乒乓球拍需要35元。妈妈买3副羽毛球拍和1副乒乓球拍一共要付( )元,当a=50时,则妈妈一共要付( )元。
9.比50克多60%是( )克,50克比( )克多60%。
10.小萍做50道口算题,做对了48道,她这次的正确率是( )。
11.在乘积1×2×3×…×98×99×100中,末尾有( )个0。
12.一个长方体的高减少3cm后成为一个正方体,表面积减少了48cm2,原来长方体的体积是( )cm3。
13.一批产品的合格率是95%,已知这批产品共有500件,则不合格的有 件。
14.按规律填空:,,,( ),。
15.把5g盐放入95g水中,盐和水的比是( ),盐占盐水的( )%。
16.看图填空。
(1)小华骑车从家里出发,送餐到相距5千米的新冠肺炎检测点,从所给的折线统计图可以看出:小华去检测点路上停车( )分,在检测点停留( )分。
(2)从检测点返回家中,速度是每小时( )千米。
17.今年弟弟6岁,哥哥15岁,当两人的年龄和为65时,弟弟( )岁。
18.如果4x=5y(x,y均不为0),那么x∶y= ∶ ,x和y成 比例。
19.一个直角三角形,两个锐角的度数比是3∶2,较小的锐角是( )度。
20.若3x2+y2+1=15,那么9x2+3y2+1=( )。
21.在一幅洗好的扑克牌中,任意抽取一张,抽到红桃与黑桃的可能性( ),抽到方块A的可能性( )。
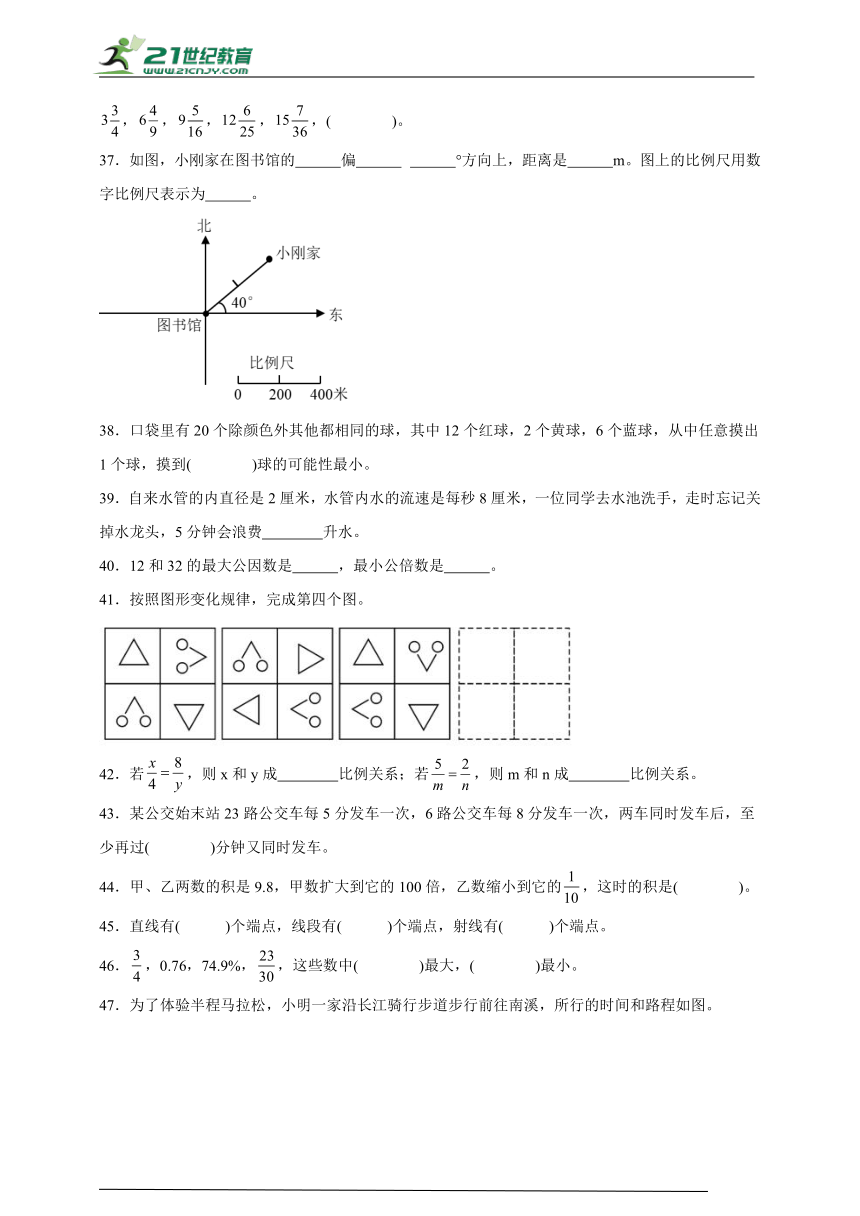
22.4÷( )=0.8==( )%。
23.一个圆锥的体积是9dm3,与它等底等高的圆柱的体积是( )dm3。
24.数学课中,老师把一个小数的小数点向右移动一位,所得的数比原来增加70.2,原来这个小数是( )。
25.一个圆锥,底面周长扩大到原来的3倍,高不变,体积扩大到原来的( )倍。
26.一个长方形的长比宽多。如果宽增加4厘米,就成为一个正方形。则原来长方形的面积是( )平方厘米。
27.根据2.4×3=0.8×9写出两个比例:( ),( )。
28.已知一个组合体是由几个相同的正方体叠合在一起组成,该组合体的从前面看与从上面看如图所示,则该组合体中正方体的个数最多是( )个。
29.一列火车从北京开往上海,3小时行了全程的,这时距中点还有40千米。这列火车平均每小时行( )千米。
30.一个圆柱的底面周长是31.4dm,高8dm,它的表面积是( )dm2,体积是( )dm3。
31.同学们站队,可以采用下面的方式进行记录。例如:
有25名同学站队,每4人站成一排,剩余1名同学,可以记录为: 有75名同学站队,每8人站成一排,剩余3名同学,可以记录为: 有128名同学站队,每16人站成一排,没有剩余的同学,可以记录为:
(1)如果有35名同学站队,每8人站成一排,可以记录为:35→8=( )。(不用写竖式)
(2)现有A名同学站队,如果A→5=0,那么A的个位数字是( )或( )。
(3)现有17名同学站队,如果17→B=3,那么B可能是( )。(写出所有情况)
(4)无论有多少名同学站队(多于10人),每m人站成一排,剩余人数一定是总人数的个位数字,那么m=( )。
32.小明读一本书,第一天读了一部分,已读的和未读的页数比是1∶5,第二天读了30页,这时已读的和未读的页数比是5∶7,这本书有( )页。
33.计算。
。
34.当x= 时,∶x的比值恰好是最小的合数。
35.将一个棱长为6dm的正方体木块削成一个最大的圆锥,那么这个圆锥的底面半径是 dm,底面周长是 dm,体积是 dm3。
36.按规律填空。
,,,,,( )。
37.如图,小刚家在图书馆的 偏 °方向上,距离是 m。图上的比例尺用数字比例尺表示为 。
38.口袋里有20个除颜色外其他都相同的球,其中12个红球,2个黄球,6个蓝球,从中任意摸出1个球,摸到( )球的可能性最小。
39.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去水池洗手,走时忘记关掉水龙头,5分钟会浪费 升水。
40.12和32的最大公因数是 ,最小公倍数是 。
41.按照图形变化规律,完成第四个图。
42.若,则x和y成 比例关系;若,则m和n成 比例关系。
43.某公交始末站23路公交车每5分发车一次,6路公交车每8分发车一次,两车同时发车后,至少再过( )分钟又同时发车。
44.甲、乙两数的积是9.8,甲数扩大到它的100倍,乙数缩小到它的,这时的积是( )。
45.直线有( )个端点,线段有( )个端点,射线有( )个端点。
46.,0.76,74.9%,,这些数中( )最大,( )最小。
47.为了体验半程马拉松,小明一家沿长江骑行步道步行前往南溪,所行的时间和路程如图。
(1)从图中可以知道小明一家步行的路程和时间成( )比例。
(2)点A表示小明一家4时走了( )千米。
48.根据前三个方格表中阴影部分的变化规律,则第(10)个方格表中阴影小正方形内的几个数字之和为 。(未画阴影)
49.节约用水是我们每个小学生的义务。学校用的自来水管内直径为0.2分米,自来水的流速一般为每秒5分米,如果你忘记关上水龙头,一分你将浪费( )升水。
50.0.39L=( )mL 28.5dm2=( )m2
96cm=( )m 5kg70g=( )kg
51.如图,直角三角形ABC中,∠B=90°,AB=6cm,BC=8cm,AC=10cm。D、E分别为BC、AC边上一点。现将三角形ABC沿线段AD对折,使得点E与点B重合。三角形ABC的面积是( )cm2,阴影部分三角形CDE的面积是( )cm2。
52.王叔叔买体育彩票中奖500万,按税法规定,取得偶然所得的个人为个人所得税的纳税义务人,应依法纳税。偶然所得以收入金额为应纳税所得额,纳税率为20%,根据规定,王叔叔应纳税 元,实际拿 元。
53.李大爷家前年甘蔗的产量是6吨,去年比前年增产20%,李大爷家去年甘蔗的产量是前年的 %,是 吨。
54.一套课桌180元,椅子的单价是桌子的50%,桌子的单价是( )元。
55.规定“※”为一种运算,对于任意两数a和b,a※b=a+0.2b,若6※x=22,则x的值为( )。
56.如图,第1个灯花有4个灯泡,第2个灯花有10个灯泡,第3个灯花有22个灯泡,……依此规律,第5个灯花有 个灯泡。
57.小亮说:“小华,我在你南偏西25°方向45m处。”小华说:“小亮,我在你 方向45m处。”
58.地球和太阳之间的平均距离约是一亿四千九百五十万千米,横线上的数写作 ,改写成用“亿”作单位的数并用四舍五入法保留一位小数约是 亿。
59.按规律填数。
1,3,7,13, 。
60.某班男生人数比全班人数的少9人,女生人数正好是全班人数的50%,全班有( )人。
《小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学西师大版》参考答案
1. 32% 百分之四十五
【分析】读百分数时,要从后往前读,先读百分号再读数(百分号前面的数);
写百分数时,要从前往后,先按照整数、小数的写法来写数字(即百分之后面的数),再写百分号,百分之写作“%”。
【详解】百分之三十二写作:32%;45%读作:百分之四十五。
【点睛】此题主要考查了百分数的读法和写法,要熟练掌握。
2.25
【分析】由图可知阴影部分长方形的宽=圆的半径r,所以阴影部分的周长相当于长方形的两条长加上圆周长的。求阴影部分周长,因为已知圆的面积和长方形面积相等,圆的面积等于,长方形的面积等于长方形的长乘r,即=长方形的长×r;所以两条长相当于圆的周长,所以阴影部分的周长:圆的周长+圆周长的=圆周长的,据此解答即可。
【详解】根据题干分析可得阴影部分周长:
20×(1+)
=20×
=25(厘米)
阴影部分的周长是25厘米。
3. 54
【分析】把45千克看作单位“1”,已知比45千克重,即这个数是45千克的(1+),用乘法计算即可;求比45千克轻千克的数,用45千克减去千克即可。
【详解】45×(1+)
=45×
=54(千克)
45-=(千克)
比45千克重是54千克;千克比45千克轻千克。
4.12.56平方厘米/12.56cm2
【分析】根据图可知,可以把右侧的三角形旋转到左边正方形右上角空白处,这样的阴影就变成了半径是4厘米的圆,根据圆的面积公式:S=πr2,代入数据求出圆的面积,再乘即可求解。
【详解】3.14×42×
=3.14×16×
=12.56(平方厘米)
图中阴影部分的面积为12.56平方厘米。
5. 40 6.7
【分析】从图中可知,平行四边形的高4cm对应的底是10cm,根据平行四边形的面积=底×高,求出这个平行四边形的面积;
已知另一条底边长是6cm,根据平行四边形的高=面积÷底,求出它对应的高,得数根据“四舍五入”法保留一位小数。
【详解】10×4=40(cm2)
40÷6≈6.7(cm)
平行四边形的面积是(40)cm2。另一条底边长是6cm,它对应的高是(6.7)cm。
6.180
【分析】根据三角形的内角和是180°,把一个三角形不管分成几个小三角形,只要是三角形,它的内角和就是180°。
【详解】把一个三角形平均分成两个小三角形,每个小三角形的内角和是180°。
【点睛】解答此题应明确:只要是三角形,它的内角和就是180°。
7.12;15;25;60
【分析】把0.6化成分数并化简是,根据比与分数的关系=3∶5,再根据比的性质比的前、后项都乘4就是12∶20;根据分数与除法的关系=3÷5,再根据商不变的性质被除数、除数都乘3就是9÷15;根据分数的基本性质,的分子、分母都乘5就是;把0.6的小数点向右移动两位添上百分号就是60%。
【详解】
12∶20=9÷15=0.6==60%
8. 3a+35 185
【分析】总价=单价×数量,据此分别求出买3副羽毛球拍和1副乒乓球拍需要的钱数,再相加即可求出一共需要的钱数,再将a=50代入需要总钱数的数量关系式即可解答。
【详解】3×a+35=(3a+35)元
当a=50时,
3×50+35
=150+35
=185(元)
妈妈买3副羽毛球拍和1副乒乓球拍一共要付元(3a+35)元,妈妈一共要付185元。
9. 80 31.25/
【分析】比50克多60%,就是求50克的(1+60%)是多少,用乘法解答;
求50克比多少克多60%,就是这个数的(1+60%)是50,求这个数用除法解答。
【详解】50×(1+60%)
=50×1.6
=80(克)
50÷(1+60%)
=50÷1.6
=31.25(克)
比50克多60%是80克,50克比31.25克多60%。
【点睛】明确求一个数的百分之几是多少,用乘法解答;已知一个数的百分之几是多少,求这个数,用除法解答是解题的关键。
10.96%
【分析】正确率是指做对的题数占总题数的百分比,计算方法是:做对的题数÷总题数×100%=正确率。
【详解】48÷50×100%
=0.96×100%
=96%
【点睛】此题属于百分率问题,都是用一部分数量(或全部数量)除以全部数量乘百分之百。
11.24
【分析】因为2×5=10,产生一个末尾的零,末尾的零也只能由以上乘式中的一个质因数2与一个质因数5相乘得到,所以只需考虑把以上乘式分解成质因数连乘以后,有多少个质因数2,有多少个质因数5,其中哪个质因数的个数少,以上乘式的末尾0的个数就和那个质因数的个数相等。
【详解】从1开始前100个自然数中有20个5的倍数,它们是5,10,15,20,25,…,95,100;在这20个数中,有4个能被25整除,它们是25,50,75,100,所以以上乘式中含有质因数5的个数:20+4=24(个),含有2的个数有50个。
因此在乘积1×2×3×…×98×99×100中,末尾有24个0。
12.112
【分析】根据题意,长方体的高减去3cm后,表面积减少48cm2,变成一个正方体,说明原来长方体的长、宽相等;减少的表面积是4个完全一样的长方形的面积,长方形的宽是3cm,长是原来长方体的长或宽,用减少的表面积除以4,求出一个长方形的面积,再除以3,即可求出原来长方体的长、宽;再用长方体的长或宽加上3cm,即是原来长方体的高;最后根据长方体的体积=长×宽×高,求出原来长方体的体积。
【详解】长方体的长、宽是:
48÷4÷3
=12÷3
=4(cm)
长方体的高是:4+3=7(cm)
长方体的体积是:
4×4×7
=16×7
=112(cm3)
原来长方体的体积是112cm3。
13.25
【分析】在此题中,一批产品的合格率是95%,不合格的占零件总个数的1-95%=5%,已知这批产品共有500件,500×(1-95%),求出结果即可。
【详解】500×(1-95%)
=500×0.05
=25(个)
【点睛】本题属于百分率应用的问题,求一个数的百分之几是多少用乘法。
14.
【分析】根据题意,后面的分数的分子依次比前面分数的分子少2,后面的分数的分母依次比前面分数的分母多2,据此解答即可。
【详解】根据分析可得:
按规律填空:,,,,。
15. 1∶19 5
【分析】求盐和水的比就是求5g与95g的比,先写出比再化成最简整数比;求盐占盐水的百分之几,用盐的质量除以盐水的质量即可解答。
【详解】5∶95=1∶19
5÷(5+95)×100%
=5÷100×100%
=5%
【点睛】求一个数是另一个数的百分之几,用除法计算。解决本题要注意是求盐占“盐水”的分率,而不是盐占水的分率。
16.(1) 20 40
(2)15
【分析】(1)通过观察折线统计图,可以看出从家出发20分钟约骑行了1.5千米,去检测点路上停留20分钟后继续前进,经过20分钟又行驶大约3.5千米到达检测点,在检测点用了40分钟,然后用了20分钟返回到家。
(2)从检测点返回家中的路程是5千米,时间是20分钟,单位换算后,利用路程除以时间即可求出速度。
【详解】(1)40-20=20(分钟)
100-60=40(分钟)
所以小华去检测点路上停车20分钟,在检测点停留40分钟。
(2)120-100=20(分钟)
20分钟=小时
5÷=15(千米/时)
【点睛】此题考查了利用折线统计图表示行走时间和行走路程的关系,以及通过观察统计图得出行走时间与路程来解决问题的方法。
17.28
【分析】根据年龄差不变,先计算年龄差15-6=9(岁),再用后来的年龄和减差,得到弟弟年龄的两倍,再除以2得弟弟的年龄。
【详解】15-6=9(岁)
(65-9)÷2
=56÷2
=28(岁)
弟弟的年龄是28岁。
18. 5 4 正
【分析】两种相关联的量,若比值一定,两种量成正比例关系;若乘积一定,两种量成反比例关系。
【详解】4x=5y,则x∶y=5∶4,5∶4=,比值一定,x和y成正比例关系。
【点睛】辨识两种相关联的量成正比例关系还是成反比例关系,就看它们是比值一定还是乘积一定。
19.36
【分析】在直角三角形中,两个锐角度数之和为90°,先用90°除以(3+2)求出一份数,再乘最小的2份,即可求出较小锐角的度数;据此解答。
【详解】90÷(3+2)×2
=90÷5×2
=18×2
=36°
所以,一个直角三角形,两个锐角的度数比是3∶2,较小的锐角是36度。
【点睛】此题考查了按比分配的应用以及直角三角形内角度数的认识。
20.43
【分析】根据等式的性质1,等式两边同时减1,等式的大小不变,则3x2+y2=14,9x2+3y2可根据乘法分配律转化为,再把14代入算式计算即可得解。
【详解】由3x2+y2+1=15得:
3x2+y2
=15-1
=14
当3x2+y2=14时
9x2+3y2+1
=3×(3x2+y2)+1
=3×14+1
=42+1
=43
21.
【分析】用包含的情况数目除以总情况数目即可求出可能性。
【详解】一副扑克牌有54张,其中红桃、黑桃、梅花、方块各13张,大、小王各一张,所以,抽到红桃的可能性与抽到黑桃的可能性都是,一样大;方块A只有1张,抽到方块A的可能性是。
【点睛】此题考查可能性的求法,可以根据数量的多少来判断。
22.5;16;80
【分析】把0.8化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;根据分数与除法的关系,=4÷5;把0.8的小数点向右移动两位添上百分号就是80%。
【详解】4÷5=0.8==80%。
【点睛】此题考查小数、分数、百分数的互化,分数与除法的关系,分数的基本性质。要牢固掌握相关知识并熟练运用。
23.27
【分析】等底等高的圆柱的体积是圆锥体积的3倍,用圆锥的体积×3,即可求出圆柱的体积。
【详解】9×3=27(dm3)
【点睛】解答本题的关键是明确等底等高的圆柱的体积是圆锥的3倍。
24.7.8
【分析】由题意可知小数点移动后的数是原数的10倍,移动后的数比原来增加70.2,然后根据差倍问题的解法,即:差÷(倍数-1)=原数,由此即可求得。
【详解】
数学课中,老师把一个小数的小数点向右移动一位,所得的数比原来增加70.2,原来这个小数是7.8。
25.9
【分析】根据圆的周长=2π×半径,一个圆锥,底面周长扩大到原来的3倍,那么圆锥底面半径也扩大到原来的3倍,再根据圆锥底面积=π×半径×半径,则圆锥底面积就扩大到原来的(3×3)倍,再根据圆锥体积=底面积×高÷3,如果高不变,体积扩大到原来的(3×3)倍,据此解答。
【详解】3×3=9
一个圆锥,底面周长扩大到原来的3倍,高不变,体积扩大到原来的9倍。
26.60
【分析】要求原来长方形的面积,需要知道原来长方形的长和宽;已知一个长方形的长比宽多,如果宽增加则与长相等;根据已知一个数的几分之几是多少,求这个数,用4除以计算出原来长方形的宽,进而求出原来长方形的长;最后根据长方形面积=长×宽,代入数值计算即可解答。
【详解】原来长方形的宽:
(厘米)
原来长方形的长:
(厘米)
原来长方形面积:10×6=60(平方厘米)
因此原来长方形的面积是60平方厘米。
27. 3∶9=0.8∶2.4 9∶3=2.4∶0.8
【分析】比例的基本性质:两个外项积等于两个内项积,写出的比例只要符合这个条件就可以。
【详解】根据2.4×3=0.8×9写出两个比例:
3∶9=0.8∶2.4
9∶3=2.4∶0.8(答案不唯一)
【点睛】熟练掌握比例的基本性质是解决此题的关键。
28.9
【分析】根据从前面和上面看到的图形可知,这个组合体一共有两层两排,下层一共有5个正方体,前排3个,后排2个且居左;上层最少有2个正方体,都在前排或后排且居左;最多有4个正方体,前排、后排各有2个且居左,据此解答。
【详解】结合从前面、从上面看到的图形,可得出以下组合体:
5+4=9(个)
该组合体中正方体的个数最多是9个。
29.80
【分析】把全程的距离看作单位“1”,已知行驶了全程的,距中点还剩();根据已知一个数的几分之几是多少,求这个数,用40除以(),计算出全程;再根据速度=路程÷时间,用全程乘计算出行驶的距离,所得积除以3,计算出这列火车平均每小时行驶多少千米。
【详解】全程:
(千米)
(千米/小时)
因此这列火车平均每小时行80千米。
30. 408.2 628
【分析】根据圆柱的底面周长求出圆柱的底面半径,再根据圆柱侧面积和体积的公式,列式解答即可。
【详解】底面半径:31.4÷3.14÷2=5(dm)
表面积:31.4×8+3.14×52×2
=251.2+157
=408.2(dm2)
体积:3.14×52×8
=78.5×8
=628(dm3)
【点睛】本题考查了对圆柱底面周长的公式、侧面积的公式和体积的公式的灵活运用。
31.(1)3
(2) 5 0
(3)7或14
(4)10
【分析】(1)35÷8=4……3,所以记录为:35→8=3;
(2)A→5=0,说明A是被除数,A是5的倍数没有余数,所以它的个位上的数字是0或5;
(3)被除数是17,余数是3,除数肯定是4的因数,14的因数有1、2、7、14,又根据余数一定要比除数小,所以1和2不符合要求,因此只有7和14是正确的;
(4)根据题意可知,m×商+余数=总数,又因为余数是总数的个位数字,所以m只能是10。
【详解】(1)如果有35名同学站队,每8人站成一排,可以记录为:35→8=3
(2)现有A名同学站队,如果A→5=0,那么A的个位数字是5或0。
(3)现有17名同学站队,如果17→B=3,那么B可能是7或14。
(4)无论有多少名同学站队(多于10人),每m人站成一排,剩余人数一定是总人数的个位数字,那么m=10。
【点睛】根据给出的几个记录可以知道,一前面的数是排队的总人数,后面的数是每排的人数,最后的结果是这样站队余下的人数。
32.120
【分析】把这本书的总页数看作单位“1”,第一天读了一部分,已读的和未读的页数比是1∶5,即已读的页数占总页数的;第二天读了30页,这时已读的和未读的页数比是5∶7,即已读的页数占总页数的;
那么第二天读的30页占总页数的(-),单位“1”未知,用第二天读的页数除以(-),即可求出这本书的总页数。
【详解】30÷(-)
=30÷(-)
=30÷(-)
=30÷
=30×4
=120(页)
这本书有120页。
33.0.5
【分析】先算,得出值是2.7。再算4.5-2.7=1.8,最后根据分数与除法的关系:分子是被除数,分母是除数得出一道除法算式,得出结果。
【详解】
=
=
=0.5
34.
【分析】最小的合数是4,可得的一个等式:∶x=4,然后再进行计算解答即可。
【详解】据分析可知:∶x=4
=4x
÷4=4x÷4
x=
【点睛】此题主要考查了最小的合数是几及利用比例的基本性质解比例。
35. 3 18.84 56.52
【分析】根据题意可知,把这个正方体木块削成一个最大的圆锥,也就是削成的圆锥的底面直径和高都等于正方体的棱长,进而求出圆锥的底面半径;再根据圆的周长公式:C=πd,圆锥的体积公式:V=πr2h,代入数据,即可解答。
【详解】6÷2=3(dm)
3.14×6=18.84(dm)
3.14×32×6
=3.14×9×6
=3.14×3×6
=9.42×6
=56.52(dm3)
【点睛】解答本题的关键明确正方体内削成最大的圆锥,圆锥的底面直径和圆锥的高等于这个正方体的棱长。
36.
【分析】整数部分依次加3;分子依次加1;分母是(分子-1)的平方。
【详解】,,,,,。
【点睛】通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
37. 东 北 40 400 1∶20000
【分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是图书馆。比例尺=图上距离∶实际距离,据此解答。
【详解】200×2=400(米)
200米=20000厘米
所以图上的比例尺用数字比例尺表示为1∶20000。
【点睛】本题主要考查图上距离、实际距离与比例尺之间的关系,并会根据物体的位置描述方向。
38.黄
【分析】在大小形状相同的情况下,哪种球的数量最多,摸到的可能性就越大;反之,哪种球的数量最少,摸到的可能性就越小,据此解答。
【详解】12>6>2,摸到黄球的可能性最小。
口袋里有20个除颜色外其他都相同的球,其中12个红球,2个黄球,6个蓝球,从中任意摸出1个球,摸到黄球的可能性最小。
39.7.536
【分析】要求5分钟会浪费多少升水,也就是求5分钟自来水管流出多少升的水;把自来水管流出来的水的体积看作是圆柱的体积;利用圆柱的体积=底面积×高,代入相应的数值计算;据此解答。
【详解】1分=60秒
3.14×(2÷2)2×8×60×5
=3.14×1×480×5
=3.14×2400
=7536(立方厘米)
7536立方厘米=7536毫升=7.536升
因此5分钟会浪费7.536升水。
40. 4 96
【分析】对于一般的两个数来说,这两个数的公有质因数的连乘积是这两个数的最大公因数,这两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;当两个数成倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数;是互质数的两个数,它们的最大公因数是1,最小公倍数即这两个数的乘积。
【详解】12=2×2×3
32=2×2×2×2×2
最大公因数是:2×2=4
最小公倍数是:2×2×3×2×2×2=96
【点睛】熟练掌握两个数的最大公因数和最小公倍数的求法是解题关键。
41.见详解
【分析】观察图形,第一幅图逆时针旋转90°得出第二幅图,第二幅图逆时针旋转90°得出第三幅图。则根据这样的规律,第四幅图是第三幅图逆时针旋转90°得出。
【详解】
42. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【详解】
xy=32(一定),乘积一定,所以x和y成反比例关系;
m∶n=5∶2=2.5(一定),比值一定,所以m和n成正比例关系。
【点睛】根据正比例意义和辨别,反比例意义和辨别进行解答。
43.40
【分析】根据题意,求出5和8的最小公倍数,它们的最小公倍数就是再次同时发车经过的时间。
【详解】5和8是互质数,它们的最小公倍数是两个数的乘积。5×8=40(分),则至少再过40分又同时发车。
【点睛】本题考查公倍数的计算及应用。理解题意,找出最小公倍数是解决本题的关键。
44.98
【分析】根据积的变化规律可知,甲、乙两数的积是9.8,甲数扩大到它的100倍,即甲数乘100,则积也乘100;乙数缩小到它的,即乙数除以10,则积也除以10;最终积乘100,再除以10,据此解答。
积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
【详解】9.8×100÷10
=980÷10
=98
这时的积是98。
45. 0 2 1
【分析】线段、射线和直线都是直的,线段有两个端点,射线只有一个端点,直线没有端点。据此解答。
【详解】直线有(0)个端点,线段有(2)个端点,射线有(1)个端点。
46. 74.9%
【分析】将分数和百分数都化成小数,再比较。分数化小数,直接用分子÷分母;百分数化小数,去掉百分号,将小数点向左移动两位即可。
【详解】、74.9%=0.749、
,0.76,74.9%,,这些数中最大,74.9%最小。
【点睛】关键是掌握百分数、分数、小数的互化方法。
47.(1)正
(2)20
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。正比例的图像是一条递增的直线,反比例的图像是一条曲线,且一个量扩大,另一个量缩小;因为路程÷时间=速度(一定),因此从图中可以知道小明一家步行的路程和时间成正比例。
(2)利用“路程÷时间=速度”,再根据“速度×时间=路程”,据此计算解答。
【详解】(1)5÷1=5
10÷2=5
15÷3=5
……
速度不变,小明一家步行的路程和时间成正比例。
(2)5÷1×4
=5×4
=20(千米)
答:点A表示小明一家4时走了20千米。
48.34
【分析】通过观察可知,阴影部分如走马灯一般,每次往左移动一格,如图:
方格的排列以4个为一个周期,用10÷4求出余数是几,第10个方格就是周期里面的第几个方格;再找到阴影部分对应的数字解答即可。
【详解】10÷4=2……2
第10个方格就是周期里面的第2个方格,如图:
据此可知阴影部分的数字分别是4、5、10、15,
4+5+10+15=34
第(10)个方格表中阴影小正方形内的几个数字之和为34。
49.9.42
【分析】可将每秒钟流水的量看作底面直径为0.2分米,高为5分米的圆柱体体积,根据圆柱的体积公式求出每秒浪费水的体积,再乘60即为一分钟浪费水的量,结果为立方分米,再将单位换算为升即可。1立方分米=1升。
【详解】1分=60秒
(立方分米)
9.42立方分米=9.42升
即如果忘记关上水龙头,一分将浪费9.42升水。
50. 390 0.285/ 0.96/ 5.07//
【分析】1L=1000mL,1m2=100dm2,1m=100cm,1kg=1000g。单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。据此解答。
【详解】0.39×1000=390,则0.39L=390mL;
28.5÷100=0.285,则28.5dm2=0.285m2;
96÷100=0.96,则96cm=0.96m;
70÷1000=0.07,5+0.07=5.07,则5kg70g=5.07kg。
51. 24 6
【分析】三角形的面积=底×高÷2,据此代入数据求出三角形ABC的面积;再据图可知,三角形CDE、三角形AED、三角形ABD的高相等,可以设高为hcm,再根据三角形CDE、三角形AED、三角形ABD的面积之和等于三角形ABC的面积列出方程,再进一步求出高ED,最后根据阴影部分三角形CDE的底是CE高是ED代入三角形的面积公式计算即可。
【详解】8×6÷2
=48÷2
=24(cm2)
CE=10-6=4(cm)
解:设ED为hcm。
6h÷2+(10-6)h÷2+6h÷2=24
3h+2h+3h=24
8h=24
h=3
4×3÷2
=12÷2
=6(cm2)
三角形ABC的面积是24cm2,阴影部分三角形CDE的面积是6cm2。
52. 1000000/100万 4000000/400万
【分析】根据应纳税额=应纳税所得额×纳税率;实际所得=应纳税所得额-应纳税额,代入相应数值计算,据此解答。
【详解】5000000×20%=1000000(元)
5000000-1000000=4000000(元)
因此根据规定,王叔叔应纳税1000000元,实际拿4000000元。
53. 120 7.2
【分析】先把前年甘蔗的产量看成单位“1”,去年比前年增产20%,则去年甘蔗的产量是去年的(1+20%),用前年的产量乘这个百分数,就是去年的产量。
【详解】1+20%=120%
6×120%=7.2(吨)
【点睛】本题的关键是找出单位“1”,已知单位“1”的量求它的百分之几是多少用乘法求解。
54.120
【分析】把桌子的单价看作单位“1”,则椅子单价的分率为50%,则180元对应的分率为(1+50%),运用除法即可求出桌子的单价。
【详解】180÷(1+50%)
=180÷150%
=120(元)
【点睛】解答本题的关键是找准单位“1”,找出180元对应的分率,根据已知一个数的百分之几是多少,求这个数用除法计算即可。
55.80
【分析】由题意可知,对于任意两数a和b,a※b=a+0.2b,则6※x=6+0.2x,又因为6※x=22,所以6+0.2x=22,然后根据等式的性质解方程即可。
【详解】6※x=6+0.2x,且6※x=22
6+0.2x=22
解:6+0.2x-6=22-6
0.2x=16
0.2x÷0.2=16÷0.2
x=80
56.94
【分析】通过观察可知,第1个灯花有(1+3)个灯泡,第2个灯花有(1+3+3×2)个灯泡,第3个灯花有(1+3+3×2+3×2×2)个灯泡,以此类推,第4个灯花有(1+3+3×2+3×2×2+3×2×2×2)个灯泡,第5个灯花有(1+3+3×2+3×2×2+3×2×2×2+3×2×2×2×2)个灯泡,据此解答。
【详解】1+3+3×2+3×2×2+3×2×2×2+3×2×2×2×2
=1+3+6+12+24+48
=94(个)
第5个灯花有94个灯泡。
【点睛】解答本题的关键根据图示发现这组图形的规律,并运用规律做题。
57.北偏东25°
【分析】根据位置的相对性可知:位置相对的两个物体所在的方向相反、角度相同、距离不变;据此解答。
【详解】小亮说:“小华,我在你南偏西25°方向45m处。”小华说:“小亮,我在你北偏东25°方向45m处。”
【点睛】根据位置的相对性进行解答。
58. 149500000 1.5
【分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,即可写出此数;改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,在数的后面带上“亿”字;再把改写成用“亿”作单位的数的百分位上的数进行四舍五入。
【详解】一亿四千九百五十万写作:149500000
149500000=1.495亿≈1.5亿
【点睛】本题主要考查整数的写法、改写和求近似数。分级读即可快速、正确地读出此数;改写和求近似数时要带计数单位。
59.21
【分析】3-1=2,2×1=2;
7-3=4,2×2=4;
13-7=6,2×3=6;
通过分析,下一个数-13=2×4,即下一个数-13=8,可得下一个数是21。
【详解】13+8=21
1,3,7,13,21
60.30
【分析】根据题意,把全班的人数看作单位“1”,因为女生人数正好是全班人数的50%,所以男生人数也是全班人数的1-50%=50%。又已知男生人数比全班人数的少9人,那么这9人就占全班人数的-50%=-=,所以全班人数为9÷=30人。
【详解】1-50%=50%
9÷(-50%)
=9÷(-)
=9÷(-)
=9÷
=9×
=30(人)
全班有30人。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.百分之三十二写作 ;45%读作: 。
2.如图中圆的周长是20厘米,且圆的面积与长方形的面积相等,那么阴影部分的周长是( )厘米。
3.比45千克重是( )千克;( )千克比45千克轻千克。
4.如图,已知长方形为8厘米,宽为4厘米,则图中阴影部分的面积为( )。
5.如图中平行四边形的面积是( )cm2。另一条底边长是6cm,它对应的高是( )cm。(保留一位小数)
6.如图所示,把一个三角形平均分成两个小三角形,每个小三角形的内角和是( )°。
7.( )∶20=9÷( )=0.6==( )%。
8.买一副羽毛球拍需要a元,买一副乒乓球拍需要35元。妈妈买3副羽毛球拍和1副乒乓球拍一共要付( )元,当a=50时,则妈妈一共要付( )元。
9.比50克多60%是( )克,50克比( )克多60%。
10.小萍做50道口算题,做对了48道,她这次的正确率是( )。
11.在乘积1×2×3×…×98×99×100中,末尾有( )个0。
12.一个长方体的高减少3cm后成为一个正方体,表面积减少了48cm2,原来长方体的体积是( )cm3。
13.一批产品的合格率是95%,已知这批产品共有500件,则不合格的有 件。
14.按规律填空:,,,( ),。
15.把5g盐放入95g水中,盐和水的比是( ),盐占盐水的( )%。
16.看图填空。
(1)小华骑车从家里出发,送餐到相距5千米的新冠肺炎检测点,从所给的折线统计图可以看出:小华去检测点路上停车( )分,在检测点停留( )分。
(2)从检测点返回家中,速度是每小时( )千米。
17.今年弟弟6岁,哥哥15岁,当两人的年龄和为65时,弟弟( )岁。
18.如果4x=5y(x,y均不为0),那么x∶y= ∶ ,x和y成 比例。
19.一个直角三角形,两个锐角的度数比是3∶2,较小的锐角是( )度。
20.若3x2+y2+1=15,那么9x2+3y2+1=( )。
21.在一幅洗好的扑克牌中,任意抽取一张,抽到红桃与黑桃的可能性( ),抽到方块A的可能性( )。
22.4÷( )=0.8==( )%。
23.一个圆锥的体积是9dm3,与它等底等高的圆柱的体积是( )dm3。
24.数学课中,老师把一个小数的小数点向右移动一位,所得的数比原来增加70.2,原来这个小数是( )。
25.一个圆锥,底面周长扩大到原来的3倍,高不变,体积扩大到原来的( )倍。
26.一个长方形的长比宽多。如果宽增加4厘米,就成为一个正方形。则原来长方形的面积是( )平方厘米。
27.根据2.4×3=0.8×9写出两个比例:( ),( )。
28.已知一个组合体是由几个相同的正方体叠合在一起组成,该组合体的从前面看与从上面看如图所示,则该组合体中正方体的个数最多是( )个。
29.一列火车从北京开往上海,3小时行了全程的,这时距中点还有40千米。这列火车平均每小时行( )千米。
30.一个圆柱的底面周长是31.4dm,高8dm,它的表面积是( )dm2,体积是( )dm3。
31.同学们站队,可以采用下面的方式进行记录。例如:
有25名同学站队,每4人站成一排,剩余1名同学,可以记录为: 有75名同学站队,每8人站成一排,剩余3名同学,可以记录为: 有128名同学站队,每16人站成一排,没有剩余的同学,可以记录为:
(1)如果有35名同学站队,每8人站成一排,可以记录为:35→8=( )。(不用写竖式)
(2)现有A名同学站队,如果A→5=0,那么A的个位数字是( )或( )。
(3)现有17名同学站队,如果17→B=3,那么B可能是( )。(写出所有情况)
(4)无论有多少名同学站队(多于10人),每m人站成一排,剩余人数一定是总人数的个位数字,那么m=( )。
32.小明读一本书,第一天读了一部分,已读的和未读的页数比是1∶5,第二天读了30页,这时已读的和未读的页数比是5∶7,这本书有( )页。
33.计算。
。
34.当x= 时,∶x的比值恰好是最小的合数。
35.将一个棱长为6dm的正方体木块削成一个最大的圆锥,那么这个圆锥的底面半径是 dm,底面周长是 dm,体积是 dm3。
36.按规律填空。
,,,,,( )。
37.如图,小刚家在图书馆的 偏 °方向上,距离是 m。图上的比例尺用数字比例尺表示为 。
38.口袋里有20个除颜色外其他都相同的球,其中12个红球,2个黄球,6个蓝球,从中任意摸出1个球,摸到( )球的可能性最小。
39.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去水池洗手,走时忘记关掉水龙头,5分钟会浪费 升水。
40.12和32的最大公因数是 ,最小公倍数是 。
41.按照图形变化规律,完成第四个图。
42.若,则x和y成 比例关系;若,则m和n成 比例关系。
43.某公交始末站23路公交车每5分发车一次,6路公交车每8分发车一次,两车同时发车后,至少再过( )分钟又同时发车。
44.甲、乙两数的积是9.8,甲数扩大到它的100倍,乙数缩小到它的,这时的积是( )。
45.直线有( )个端点,线段有( )个端点,射线有( )个端点。
46.,0.76,74.9%,,这些数中( )最大,( )最小。
47.为了体验半程马拉松,小明一家沿长江骑行步道步行前往南溪,所行的时间和路程如图。
(1)从图中可以知道小明一家步行的路程和时间成( )比例。
(2)点A表示小明一家4时走了( )千米。
48.根据前三个方格表中阴影部分的变化规律,则第(10)个方格表中阴影小正方形内的几个数字之和为 。(未画阴影)
49.节约用水是我们每个小学生的义务。学校用的自来水管内直径为0.2分米,自来水的流速一般为每秒5分米,如果你忘记关上水龙头,一分你将浪费( )升水。
50.0.39L=( )mL 28.5dm2=( )m2
96cm=( )m 5kg70g=( )kg
51.如图,直角三角形ABC中,∠B=90°,AB=6cm,BC=8cm,AC=10cm。D、E分别为BC、AC边上一点。现将三角形ABC沿线段AD对折,使得点E与点B重合。三角形ABC的面积是( )cm2,阴影部分三角形CDE的面积是( )cm2。
52.王叔叔买体育彩票中奖500万,按税法规定,取得偶然所得的个人为个人所得税的纳税义务人,应依法纳税。偶然所得以收入金额为应纳税所得额,纳税率为20%,根据规定,王叔叔应纳税 元,实际拿 元。
53.李大爷家前年甘蔗的产量是6吨,去年比前年增产20%,李大爷家去年甘蔗的产量是前年的 %,是 吨。
54.一套课桌180元,椅子的单价是桌子的50%,桌子的单价是( )元。
55.规定“※”为一种运算,对于任意两数a和b,a※b=a+0.2b,若6※x=22,则x的值为( )。
56.如图,第1个灯花有4个灯泡,第2个灯花有10个灯泡,第3个灯花有22个灯泡,……依此规律,第5个灯花有 个灯泡。
57.小亮说:“小华,我在你南偏西25°方向45m处。”小华说:“小亮,我在你 方向45m处。”
58.地球和太阳之间的平均距离约是一亿四千九百五十万千米,横线上的数写作 ,改写成用“亿”作单位的数并用四舍五入法保留一位小数约是 亿。
59.按规律填数。
1,3,7,13, 。
60.某班男生人数比全班人数的少9人,女生人数正好是全班人数的50%,全班有( )人。
《小升初暑假专项提升测试卷:填空题(含解析)-2024-2025学年下学期小学数学西师大版》参考答案
1. 32% 百分之四十五
【分析】读百分数时,要从后往前读,先读百分号再读数(百分号前面的数);
写百分数时,要从前往后,先按照整数、小数的写法来写数字(即百分之后面的数),再写百分号,百分之写作“%”。
【详解】百分之三十二写作:32%;45%读作:百分之四十五。
【点睛】此题主要考查了百分数的读法和写法,要熟练掌握。
2.25
【分析】由图可知阴影部分长方形的宽=圆的半径r,所以阴影部分的周长相当于长方形的两条长加上圆周长的。求阴影部分周长,因为已知圆的面积和长方形面积相等,圆的面积等于,长方形的面积等于长方形的长乘r,即=长方形的长×r;所以两条长相当于圆的周长,所以阴影部分的周长:圆的周长+圆周长的=圆周长的,据此解答即可。
【详解】根据题干分析可得阴影部分周长:
20×(1+)
=20×
=25(厘米)
阴影部分的周长是25厘米。
3. 54
【分析】把45千克看作单位“1”,已知比45千克重,即这个数是45千克的(1+),用乘法计算即可;求比45千克轻千克的数,用45千克减去千克即可。
【详解】45×(1+)
=45×
=54(千克)
45-=(千克)
比45千克重是54千克;千克比45千克轻千克。
4.12.56平方厘米/12.56cm2
【分析】根据图可知,可以把右侧的三角形旋转到左边正方形右上角空白处,这样的阴影就变成了半径是4厘米的圆,根据圆的面积公式:S=πr2,代入数据求出圆的面积,再乘即可求解。
【详解】3.14×42×
=3.14×16×
=12.56(平方厘米)
图中阴影部分的面积为12.56平方厘米。
5. 40 6.7
【分析】从图中可知,平行四边形的高4cm对应的底是10cm,根据平行四边形的面积=底×高,求出这个平行四边形的面积;
已知另一条底边长是6cm,根据平行四边形的高=面积÷底,求出它对应的高,得数根据“四舍五入”法保留一位小数。
【详解】10×4=40(cm2)
40÷6≈6.7(cm)
平行四边形的面积是(40)cm2。另一条底边长是6cm,它对应的高是(6.7)cm。
6.180
【分析】根据三角形的内角和是180°,把一个三角形不管分成几个小三角形,只要是三角形,它的内角和就是180°。
【详解】把一个三角形平均分成两个小三角形,每个小三角形的内角和是180°。
【点睛】解答此题应明确:只要是三角形,它的内角和就是180°。
7.12;15;25;60
【分析】把0.6化成分数并化简是,根据比与分数的关系=3∶5,再根据比的性质比的前、后项都乘4就是12∶20;根据分数与除法的关系=3÷5,再根据商不变的性质被除数、除数都乘3就是9÷15;根据分数的基本性质,的分子、分母都乘5就是;把0.6的小数点向右移动两位添上百分号就是60%。
【详解】
12∶20=9÷15=0.6==60%
8. 3a+35 185
【分析】总价=单价×数量,据此分别求出买3副羽毛球拍和1副乒乓球拍需要的钱数,再相加即可求出一共需要的钱数,再将a=50代入需要总钱数的数量关系式即可解答。
【详解】3×a+35=(3a+35)元
当a=50时,
3×50+35
=150+35
=185(元)
妈妈买3副羽毛球拍和1副乒乓球拍一共要付元(3a+35)元,妈妈一共要付185元。
9. 80 31.25/
【分析】比50克多60%,就是求50克的(1+60%)是多少,用乘法解答;
求50克比多少克多60%,就是这个数的(1+60%)是50,求这个数用除法解答。
【详解】50×(1+60%)
=50×1.6
=80(克)
50÷(1+60%)
=50÷1.6
=31.25(克)
比50克多60%是80克,50克比31.25克多60%。
【点睛】明确求一个数的百分之几是多少,用乘法解答;已知一个数的百分之几是多少,求这个数,用除法解答是解题的关键。
10.96%
【分析】正确率是指做对的题数占总题数的百分比,计算方法是:做对的题数÷总题数×100%=正确率。
【详解】48÷50×100%
=0.96×100%
=96%
【点睛】此题属于百分率问题,都是用一部分数量(或全部数量)除以全部数量乘百分之百。
11.24
【分析】因为2×5=10,产生一个末尾的零,末尾的零也只能由以上乘式中的一个质因数2与一个质因数5相乘得到,所以只需考虑把以上乘式分解成质因数连乘以后,有多少个质因数2,有多少个质因数5,其中哪个质因数的个数少,以上乘式的末尾0的个数就和那个质因数的个数相等。
【详解】从1开始前100个自然数中有20个5的倍数,它们是5,10,15,20,25,…,95,100;在这20个数中,有4个能被25整除,它们是25,50,75,100,所以以上乘式中含有质因数5的个数:20+4=24(个),含有2的个数有50个。
因此在乘积1×2×3×…×98×99×100中,末尾有24个0。
12.112
【分析】根据题意,长方体的高减去3cm后,表面积减少48cm2,变成一个正方体,说明原来长方体的长、宽相等;减少的表面积是4个完全一样的长方形的面积,长方形的宽是3cm,长是原来长方体的长或宽,用减少的表面积除以4,求出一个长方形的面积,再除以3,即可求出原来长方体的长、宽;再用长方体的长或宽加上3cm,即是原来长方体的高;最后根据长方体的体积=长×宽×高,求出原来长方体的体积。
【详解】长方体的长、宽是:
48÷4÷3
=12÷3
=4(cm)
长方体的高是:4+3=7(cm)
长方体的体积是:
4×4×7
=16×7
=112(cm3)
原来长方体的体积是112cm3。
13.25
【分析】在此题中,一批产品的合格率是95%,不合格的占零件总个数的1-95%=5%,已知这批产品共有500件,500×(1-95%),求出结果即可。
【详解】500×(1-95%)
=500×0.05
=25(个)
【点睛】本题属于百分率应用的问题,求一个数的百分之几是多少用乘法。
14.
【分析】根据题意,后面的分数的分子依次比前面分数的分子少2,后面的分数的分母依次比前面分数的分母多2,据此解答即可。
【详解】根据分析可得:
按规律填空:,,,,。
15. 1∶19 5
【分析】求盐和水的比就是求5g与95g的比,先写出比再化成最简整数比;求盐占盐水的百分之几,用盐的质量除以盐水的质量即可解答。
【详解】5∶95=1∶19
5÷(5+95)×100%
=5÷100×100%
=5%
【点睛】求一个数是另一个数的百分之几,用除法计算。解决本题要注意是求盐占“盐水”的分率,而不是盐占水的分率。
16.(1) 20 40
(2)15
【分析】(1)通过观察折线统计图,可以看出从家出发20分钟约骑行了1.5千米,去检测点路上停留20分钟后继续前进,经过20分钟又行驶大约3.5千米到达检测点,在检测点用了40分钟,然后用了20分钟返回到家。
(2)从检测点返回家中的路程是5千米,时间是20分钟,单位换算后,利用路程除以时间即可求出速度。
【详解】(1)40-20=20(分钟)
100-60=40(分钟)
所以小华去检测点路上停车20分钟,在检测点停留40分钟。
(2)120-100=20(分钟)
20分钟=小时
5÷=15(千米/时)
【点睛】此题考查了利用折线统计图表示行走时间和行走路程的关系,以及通过观察统计图得出行走时间与路程来解决问题的方法。
17.28
【分析】根据年龄差不变,先计算年龄差15-6=9(岁),再用后来的年龄和减差,得到弟弟年龄的两倍,再除以2得弟弟的年龄。
【详解】15-6=9(岁)
(65-9)÷2
=56÷2
=28(岁)
弟弟的年龄是28岁。
18. 5 4 正
【分析】两种相关联的量,若比值一定,两种量成正比例关系;若乘积一定,两种量成反比例关系。
【详解】4x=5y,则x∶y=5∶4,5∶4=,比值一定,x和y成正比例关系。
【点睛】辨识两种相关联的量成正比例关系还是成反比例关系,就看它们是比值一定还是乘积一定。
19.36
【分析】在直角三角形中,两个锐角度数之和为90°,先用90°除以(3+2)求出一份数,再乘最小的2份,即可求出较小锐角的度数;据此解答。
【详解】90÷(3+2)×2
=90÷5×2
=18×2
=36°
所以,一个直角三角形,两个锐角的度数比是3∶2,较小的锐角是36度。
【点睛】此题考查了按比分配的应用以及直角三角形内角度数的认识。
20.43
【分析】根据等式的性质1,等式两边同时减1,等式的大小不变,则3x2+y2=14,9x2+3y2可根据乘法分配律转化为,再把14代入算式计算即可得解。
【详解】由3x2+y2+1=15得:
3x2+y2
=15-1
=14
当3x2+y2=14时
9x2+3y2+1
=3×(3x2+y2)+1
=3×14+1
=42+1
=43
21.
【分析】用包含的情况数目除以总情况数目即可求出可能性。
【详解】一副扑克牌有54张,其中红桃、黑桃、梅花、方块各13张,大、小王各一张,所以,抽到红桃的可能性与抽到黑桃的可能性都是,一样大;方块A只有1张,抽到方块A的可能性是。
【点睛】此题考查可能性的求法,可以根据数量的多少来判断。
22.5;16;80
【分析】把0.8化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;根据分数与除法的关系,=4÷5;把0.8的小数点向右移动两位添上百分号就是80%。
【详解】4÷5=0.8==80%。
【点睛】此题考查小数、分数、百分数的互化,分数与除法的关系,分数的基本性质。要牢固掌握相关知识并熟练运用。
23.27
【分析】等底等高的圆柱的体积是圆锥体积的3倍,用圆锥的体积×3,即可求出圆柱的体积。
【详解】9×3=27(dm3)
【点睛】解答本题的关键是明确等底等高的圆柱的体积是圆锥的3倍。
24.7.8
【分析】由题意可知小数点移动后的数是原数的10倍,移动后的数比原来增加70.2,然后根据差倍问题的解法,即:差÷(倍数-1)=原数,由此即可求得。
【详解】
数学课中,老师把一个小数的小数点向右移动一位,所得的数比原来增加70.2,原来这个小数是7.8。
25.9
【分析】根据圆的周长=2π×半径,一个圆锥,底面周长扩大到原来的3倍,那么圆锥底面半径也扩大到原来的3倍,再根据圆锥底面积=π×半径×半径,则圆锥底面积就扩大到原来的(3×3)倍,再根据圆锥体积=底面积×高÷3,如果高不变,体积扩大到原来的(3×3)倍,据此解答。
【详解】3×3=9
一个圆锥,底面周长扩大到原来的3倍,高不变,体积扩大到原来的9倍。
26.60
【分析】要求原来长方形的面积,需要知道原来长方形的长和宽;已知一个长方形的长比宽多,如果宽增加则与长相等;根据已知一个数的几分之几是多少,求这个数,用4除以计算出原来长方形的宽,进而求出原来长方形的长;最后根据长方形面积=长×宽,代入数值计算即可解答。
【详解】原来长方形的宽:
(厘米)
原来长方形的长:
(厘米)
原来长方形面积:10×6=60(平方厘米)
因此原来长方形的面积是60平方厘米。
27. 3∶9=0.8∶2.4 9∶3=2.4∶0.8
【分析】比例的基本性质:两个外项积等于两个内项积,写出的比例只要符合这个条件就可以。
【详解】根据2.4×3=0.8×9写出两个比例:
3∶9=0.8∶2.4
9∶3=2.4∶0.8(答案不唯一)
【点睛】熟练掌握比例的基本性质是解决此题的关键。
28.9
【分析】根据从前面和上面看到的图形可知,这个组合体一共有两层两排,下层一共有5个正方体,前排3个,后排2个且居左;上层最少有2个正方体,都在前排或后排且居左;最多有4个正方体,前排、后排各有2个且居左,据此解答。
【详解】结合从前面、从上面看到的图形,可得出以下组合体:
5+4=9(个)
该组合体中正方体的个数最多是9个。
29.80
【分析】把全程的距离看作单位“1”,已知行驶了全程的,距中点还剩();根据已知一个数的几分之几是多少,求这个数,用40除以(),计算出全程;再根据速度=路程÷时间,用全程乘计算出行驶的距离,所得积除以3,计算出这列火车平均每小时行驶多少千米。
【详解】全程:
(千米)
(千米/小时)
因此这列火车平均每小时行80千米。
30. 408.2 628
【分析】根据圆柱的底面周长求出圆柱的底面半径,再根据圆柱侧面积和体积的公式,列式解答即可。
【详解】底面半径:31.4÷3.14÷2=5(dm)
表面积:31.4×8+3.14×52×2
=251.2+157
=408.2(dm2)
体积:3.14×52×8
=78.5×8
=628(dm3)
【点睛】本题考查了对圆柱底面周长的公式、侧面积的公式和体积的公式的灵活运用。
31.(1)3
(2) 5 0
(3)7或14
(4)10
【分析】(1)35÷8=4……3,所以记录为:35→8=3;
(2)A→5=0,说明A是被除数,A是5的倍数没有余数,所以它的个位上的数字是0或5;
(3)被除数是17,余数是3,除数肯定是4的因数,14的因数有1、2、7、14,又根据余数一定要比除数小,所以1和2不符合要求,因此只有7和14是正确的;
(4)根据题意可知,m×商+余数=总数,又因为余数是总数的个位数字,所以m只能是10。
【详解】(1)如果有35名同学站队,每8人站成一排,可以记录为:35→8=3
(2)现有A名同学站队,如果A→5=0,那么A的个位数字是5或0。
(3)现有17名同学站队,如果17→B=3,那么B可能是7或14。
(4)无论有多少名同学站队(多于10人),每m人站成一排,剩余人数一定是总人数的个位数字,那么m=10。
【点睛】根据给出的几个记录可以知道,一前面的数是排队的总人数,后面的数是每排的人数,最后的结果是这样站队余下的人数。
32.120
【分析】把这本书的总页数看作单位“1”,第一天读了一部分,已读的和未读的页数比是1∶5,即已读的页数占总页数的;第二天读了30页,这时已读的和未读的页数比是5∶7,即已读的页数占总页数的;
那么第二天读的30页占总页数的(-),单位“1”未知,用第二天读的页数除以(-),即可求出这本书的总页数。
【详解】30÷(-)
=30÷(-)
=30÷(-)
=30÷
=30×4
=120(页)
这本书有120页。
33.0.5
【分析】先算,得出值是2.7。再算4.5-2.7=1.8,最后根据分数与除法的关系:分子是被除数,分母是除数得出一道除法算式,得出结果。
【详解】
=
=
=0.5
34.
【分析】最小的合数是4,可得的一个等式:∶x=4,然后再进行计算解答即可。
【详解】据分析可知:∶x=4
=4x
÷4=4x÷4
x=
【点睛】此题主要考查了最小的合数是几及利用比例的基本性质解比例。
35. 3 18.84 56.52
【分析】根据题意可知,把这个正方体木块削成一个最大的圆锥,也就是削成的圆锥的底面直径和高都等于正方体的棱长,进而求出圆锥的底面半径;再根据圆的周长公式:C=πd,圆锥的体积公式:V=πr2h,代入数据,即可解答。
【详解】6÷2=3(dm)
3.14×6=18.84(dm)
3.14×32×6
=3.14×9×6
=3.14×3×6
=9.42×6
=56.52(dm3)
【点睛】解答本题的关键明确正方体内削成最大的圆锥,圆锥的底面直径和圆锥的高等于这个正方体的棱长。
36.
【分析】整数部分依次加3;分子依次加1;分母是(分子-1)的平方。
【详解】,,,,,。
【点睛】通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
37. 东 北 40 400 1∶20000
【分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是图书馆。比例尺=图上距离∶实际距离,据此解答。
【详解】200×2=400(米)
200米=20000厘米
所以图上的比例尺用数字比例尺表示为1∶20000。
【点睛】本题主要考查图上距离、实际距离与比例尺之间的关系,并会根据物体的位置描述方向。
38.黄
【分析】在大小形状相同的情况下,哪种球的数量最多,摸到的可能性就越大;反之,哪种球的数量最少,摸到的可能性就越小,据此解答。
【详解】12>6>2,摸到黄球的可能性最小。
口袋里有20个除颜色外其他都相同的球,其中12个红球,2个黄球,6个蓝球,从中任意摸出1个球,摸到黄球的可能性最小。
39.7.536
【分析】要求5分钟会浪费多少升水,也就是求5分钟自来水管流出多少升的水;把自来水管流出来的水的体积看作是圆柱的体积;利用圆柱的体积=底面积×高,代入相应的数值计算;据此解答。
【详解】1分=60秒
3.14×(2÷2)2×8×60×5
=3.14×1×480×5
=3.14×2400
=7536(立方厘米)
7536立方厘米=7536毫升=7.536升
因此5分钟会浪费7.536升水。
40. 4 96
【分析】对于一般的两个数来说,这两个数的公有质因数的连乘积是这两个数的最大公因数,这两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;当两个数成倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数;是互质数的两个数,它们的最大公因数是1,最小公倍数即这两个数的乘积。
【详解】12=2×2×3
32=2×2×2×2×2
最大公因数是:2×2=4
最小公倍数是:2×2×3×2×2×2=96
【点睛】熟练掌握两个数的最大公因数和最小公倍数的求法是解题关键。
41.见详解
【分析】观察图形,第一幅图逆时针旋转90°得出第二幅图,第二幅图逆时针旋转90°得出第三幅图。则根据这样的规律,第四幅图是第三幅图逆时针旋转90°得出。
【详解】
42. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【详解】
xy=32(一定),乘积一定,所以x和y成反比例关系;
m∶n=5∶2=2.5(一定),比值一定,所以m和n成正比例关系。
【点睛】根据正比例意义和辨别,反比例意义和辨别进行解答。
43.40
【分析】根据题意,求出5和8的最小公倍数,它们的最小公倍数就是再次同时发车经过的时间。
【详解】5和8是互质数,它们的最小公倍数是两个数的乘积。5×8=40(分),则至少再过40分又同时发车。
【点睛】本题考查公倍数的计算及应用。理解题意,找出最小公倍数是解决本题的关键。
44.98
【分析】根据积的变化规律可知,甲、乙两数的积是9.8,甲数扩大到它的100倍,即甲数乘100,则积也乘100;乙数缩小到它的,即乙数除以10,则积也除以10;最终积乘100,再除以10,据此解答。
积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
【详解】9.8×100÷10
=980÷10
=98
这时的积是98。
45. 0 2 1
【分析】线段、射线和直线都是直的,线段有两个端点,射线只有一个端点,直线没有端点。据此解答。
【详解】直线有(0)个端点,线段有(2)个端点,射线有(1)个端点。
46. 74.9%
【分析】将分数和百分数都化成小数,再比较。分数化小数,直接用分子÷分母;百分数化小数,去掉百分号,将小数点向左移动两位即可。
【详解】、74.9%=0.749、
,0.76,74.9%,,这些数中最大,74.9%最小。
【点睛】关键是掌握百分数、分数、小数的互化方法。
47.(1)正
(2)20
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。正比例的图像是一条递增的直线,反比例的图像是一条曲线,且一个量扩大,另一个量缩小;因为路程÷时间=速度(一定),因此从图中可以知道小明一家步行的路程和时间成正比例。
(2)利用“路程÷时间=速度”,再根据“速度×时间=路程”,据此计算解答。
【详解】(1)5÷1=5
10÷2=5
15÷3=5
……
速度不变,小明一家步行的路程和时间成正比例。
(2)5÷1×4
=5×4
=20(千米)
答:点A表示小明一家4时走了20千米。
48.34
【分析】通过观察可知,阴影部分如走马灯一般,每次往左移动一格,如图:
方格的排列以4个为一个周期,用10÷4求出余数是几,第10个方格就是周期里面的第几个方格;再找到阴影部分对应的数字解答即可。
【详解】10÷4=2……2
第10个方格就是周期里面的第2个方格,如图:
据此可知阴影部分的数字分别是4、5、10、15,
4+5+10+15=34
第(10)个方格表中阴影小正方形内的几个数字之和为34。
49.9.42
【分析】可将每秒钟流水的量看作底面直径为0.2分米,高为5分米的圆柱体体积,根据圆柱的体积公式求出每秒浪费水的体积,再乘60即为一分钟浪费水的量,结果为立方分米,再将单位换算为升即可。1立方分米=1升。
【详解】1分=60秒
(立方分米)
9.42立方分米=9.42升
即如果忘记关上水龙头,一分将浪费9.42升水。
50. 390 0.285/ 0.96/ 5.07//
【分析】1L=1000mL,1m2=100dm2,1m=100cm,1kg=1000g。单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。据此解答。
【详解】0.39×1000=390,则0.39L=390mL;
28.5÷100=0.285,则28.5dm2=0.285m2;
96÷100=0.96,则96cm=0.96m;
70÷1000=0.07,5+0.07=5.07,则5kg70g=5.07kg。
51. 24 6
【分析】三角形的面积=底×高÷2,据此代入数据求出三角形ABC的面积;再据图可知,三角形CDE、三角形AED、三角形ABD的高相等,可以设高为hcm,再根据三角形CDE、三角形AED、三角形ABD的面积之和等于三角形ABC的面积列出方程,再进一步求出高ED,最后根据阴影部分三角形CDE的底是CE高是ED代入三角形的面积公式计算即可。
【详解】8×6÷2
=48÷2
=24(cm2)
CE=10-6=4(cm)
解:设ED为hcm。
6h÷2+(10-6)h÷2+6h÷2=24
3h+2h+3h=24
8h=24
h=3
4×3÷2
=12÷2
=6(cm2)
三角形ABC的面积是24cm2,阴影部分三角形CDE的面积是6cm2。
52. 1000000/100万 4000000/400万
【分析】根据应纳税额=应纳税所得额×纳税率;实际所得=应纳税所得额-应纳税额,代入相应数值计算,据此解答。
【详解】5000000×20%=1000000(元)
5000000-1000000=4000000(元)
因此根据规定,王叔叔应纳税1000000元,实际拿4000000元。
53. 120 7.2
【分析】先把前年甘蔗的产量看成单位“1”,去年比前年增产20%,则去年甘蔗的产量是去年的(1+20%),用前年的产量乘这个百分数,就是去年的产量。
【详解】1+20%=120%
6×120%=7.2(吨)
【点睛】本题的关键是找出单位“1”,已知单位“1”的量求它的百分之几是多少用乘法求解。
54.120
【分析】把桌子的单价看作单位“1”,则椅子单价的分率为50%,则180元对应的分率为(1+50%),运用除法即可求出桌子的单价。
【详解】180÷(1+50%)
=180÷150%
=120(元)
【点睛】解答本题的关键是找准单位“1”,找出180元对应的分率,根据已知一个数的百分之几是多少,求这个数用除法计算即可。
55.80
【分析】由题意可知,对于任意两数a和b,a※b=a+0.2b,则6※x=6+0.2x,又因为6※x=22,所以6+0.2x=22,然后根据等式的性质解方程即可。
【详解】6※x=6+0.2x,且6※x=22
6+0.2x=22
解:6+0.2x-6=22-6
0.2x=16
0.2x÷0.2=16÷0.2
x=80
56.94
【分析】通过观察可知,第1个灯花有(1+3)个灯泡,第2个灯花有(1+3+3×2)个灯泡,第3个灯花有(1+3+3×2+3×2×2)个灯泡,以此类推,第4个灯花有(1+3+3×2+3×2×2+3×2×2×2)个灯泡,第5个灯花有(1+3+3×2+3×2×2+3×2×2×2+3×2×2×2×2)个灯泡,据此解答。
【详解】1+3+3×2+3×2×2+3×2×2×2+3×2×2×2×2
=1+3+6+12+24+48
=94(个)
第5个灯花有94个灯泡。
【点睛】解答本题的关键根据图示发现这组图形的规律,并运用规律做题。
57.北偏东25°
【分析】根据位置的相对性可知:位置相对的两个物体所在的方向相反、角度相同、距离不变;据此解答。
【详解】小亮说:“小华,我在你南偏西25°方向45m处。”小华说:“小亮,我在你北偏东25°方向45m处。”
【点睛】根据位置的相对性进行解答。
58. 149500000 1.5
【分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,即可写出此数;改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,在数的后面带上“亿”字;再把改写成用“亿”作单位的数的百分位上的数进行四舍五入。
【详解】一亿四千九百五十万写作:149500000
149500000=1.495亿≈1.5亿
【点睛】本题主要考查整数的写法、改写和求近似数。分级读即可快速、正确地读出此数;改写和求近似数时要带计数单位。
59.21
【分析】3-1=2,2×1=2;
7-3=4,2×2=4;
13-7=6,2×3=6;
通过分析,下一个数-13=2×4,即下一个数-13=8,可得下一个数是21。
【详解】13+8=21
1,3,7,13,21
60.30
【分析】根据题意,把全班的人数看作单位“1”,因为女生人数正好是全班人数的50%,所以男生人数也是全班人数的1-50%=50%。又已知男生人数比全班人数的少9人,那么这9人就占全班人数的-50%=-=,所以全班人数为9÷=30人。
【详解】1-50%=50%
9÷(-50%)
=9÷(-)
=9÷(-)
=9÷
=9×
=30(人)
全班有30人。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
