专题提优特训6 线段计算中的数学思想 提优训练(含答案)2025-2026学年人教版七年级数学上册
文档属性
| 名称 | 专题提优特训6 线段计算中的数学思想 提优训练(含答案)2025-2026学年人教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 122.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-17 15:19:05 | ||
图片预览


文档简介
专题提优特训6 线段计算中的数学思想
题型1数形结合思想
1.已知点 B,C在线段AD 上.
(1)如图,共有 条线段;
(2)如图,AB=CD.
①比较线段的大小:AC BD(填“>”“=”或“<”);
②若BD=4AB,BC=12cm,则 AD 的长为 cm;
(3)若AB:CD=1:2,且 E 为 BC 中点,求AE 与BD 的数量关系.(温馨提醒:重新画图)
题型2 整体思想
2.(2024·济南历下区二模)如图,C,D 是线段AB 上两点,且CD=3AD--2BC,则AC与BD 的数量关系是( ).
A. AC=BD B. 2AC=BD
C. 3AC=2BD D. 4AC=3BD
3.(1)如图,点 C 在线段AB 上,点 M 在线段AC上,点 N 在线段 BC 上.
①已知AC=13,CB=8,若点 M,N 分别是AC,BC 的中点,求线段 MN 的长;
②已知AC=13,CB=8,若点 M 是AC 的中点, 求线段MN 的长;
③已知AC=a,CB=b,若 请直接写出线段 MN 的长(用含a,b的式子表示);
(2)若点 C 在直线AB 上,(1)中其他条件不变,已知 3BN=2CN,请直接写出线段 MN 的长.
题型3 方程思想
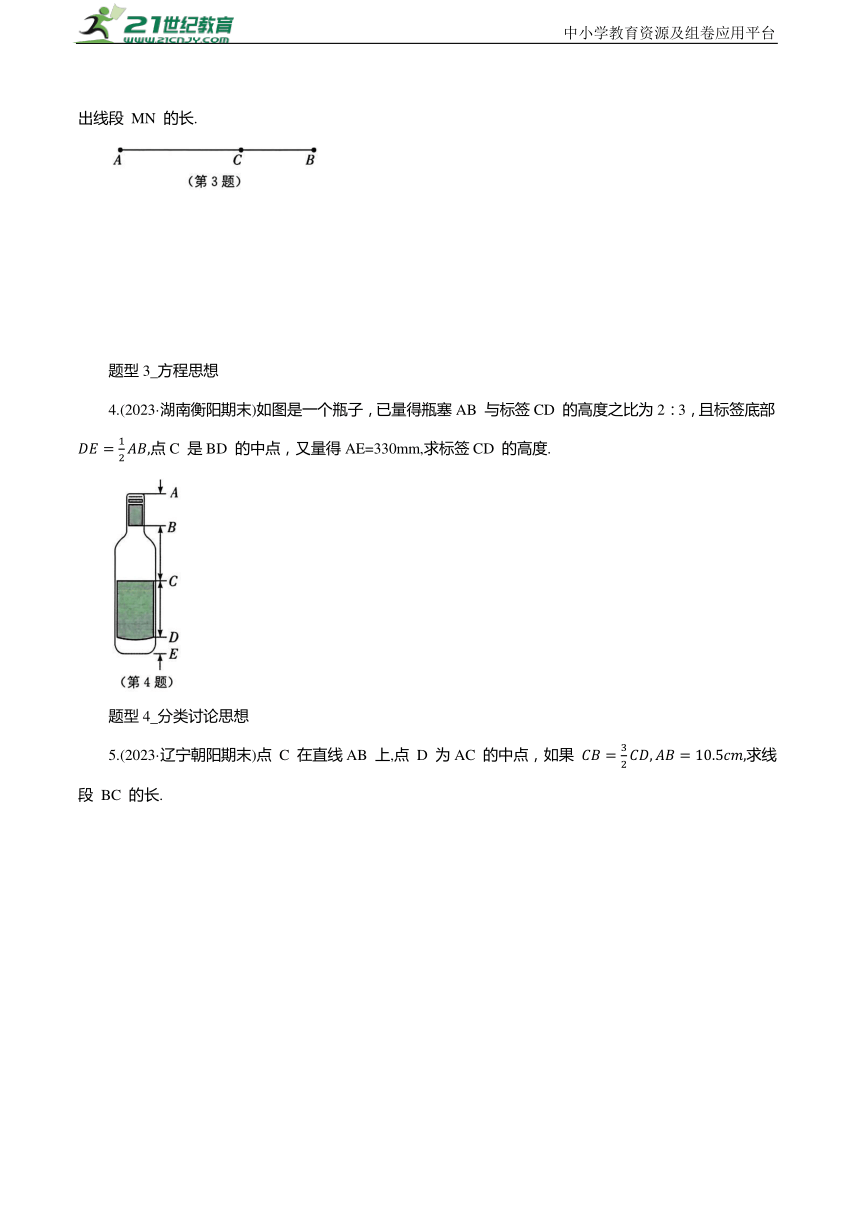
4.(2023·湖南衡阳期末)如图是一个瓶子,已量得瓶塞AB 与标签CD 的高度之比为2:3,且标签底部 点C 是BD 的中点,又量得AE=330mm,求标签CD 的高度.
题型4 分类讨论思想
5.(2023·辽宁朝阳期末)点 C 在直线AB 上,点 D 为AC 的中点,如果 求线段 BC 的长.
6.(2024·江苏扬州期末)如图,已知线段AB=12cm,点C为AB 上一点且AC=3cm,点 P 是BC的中点.
(1)求CP 的长度;
(2)点 D 是直线AB 上一点,且 CD+BD=13cm,求CD 的长.
7.中考新考法 新定义问题(2024·河北邢台期中)[新知理解]
点 C 在线段AB 上,若 BC=2AC 或AC=2BC,则称点 C 是线段AB 的“优点”,线段AC,BC 称作互为“优点”伴侣线段.
例如,图(1)中线段AB 的长度为6,点C 在AB 上,AC 的长度为2,则点 C 是线段AB 的其中一个“优点”.
(1)若点 C 为图(1)中线段 AB 的“优点”,AC=6(AC(2)若点 D 也是图(1)中线段 AB 的“优点”(不同于点C),AC=6,则AC BD(填“=”或“≠”);
[解决问题]
如图(2),数轴上有 E,F两点,其中点 E 表示的数为1,点F 表示的数为4.
(3)若点 M 在点N 的左侧,且M,N均为线段OF 的“优点”,求线段 MN 的长;
(4)若点 G 在线段EF 的延长线上,且线段EF 与GF 互为“优点”伴侣线段,求点 G 表示的数.
中小学教育资源及组卷应用平台
题型1 数形结合思想
1.已知点 B,C在线段AD 上.
(1)如图,共有 6 条线段;
(2)如图,AB=CD.
①比较线段的大小:AC = BD(填“>”“=”或“<”);
②若BD=4AB,BC=12cm,则AD 的长为 20 cm;
(3)若AB:CD=1:2,且 E 为BC 中点,求AE 与BD 的数量关系.(温馨提醒:重新画图)
解:如图(1),当点C在AB的延长线上,
如图(2),当点C在线段AB上时,
题型2 整体思想
2.(2024·济南历下区二模)如图,C,D 是线段AB 上两点,且CD=3AD-2BC,则AC与BD 的数量关系是(C ).
A. AC=BD B. 2AC=BD
C. 3AC=2BD D. 4AC=3BD
3.(1)如图,点C 在线段AB 上,点 M 在线段AC上,点N 在线段BC上.
①已知AC=13,CB=8,若点 M,N 分别是AC,BC 的中点,求线段 MN 的长;
②已知AC=13,CB=8,若点 M 是AC 的中点, 求线段MN 的长;
③已知AC=a,CB=b,若 请直接写出线段 MN 的长(用含a,b的式子表示);
(2)若点 C 在直线AB 上,(1)中其他条件不变,已知 3BN=2CN,请直接写出线段MN 的长.
解:(1)①MN 的长为10.5.
②MN 的长为8.5.
(2)MN 的长为 或
题型3 方程思想
4.(2023·湖南衡阳期末)如图是一个瓶子,已量得瓶塞AB 与标签CD 的高度之比为2:3,且标签底部 点C 是BD的中点,又量得AE=330mm,求标签CD 的高度.
解:设DE的长为x mm.
∴AB=2DE=2x mm.
由AB:CD=2:3,AB=2x mm,得CD=3x mm.
∵点C 是BD 的中点,
∴BC=CD=3x mm.
∵AE=330 mm,∴AB+BC+CD+DE= 3x=110mm,
∴标签CD的高度为110mm.
题型4 分类讨论思想
5.(2023·辽宁朝阳期末)点C 在直线AB上,点 D 为AC 的中点,如果 求线段BC的长.
解:由 得
由D 是AC 的中点,得
①如图(1),当点C在线段AB 的延长线上时,
由线段的和差关系,得AD+CD-BC=AB,即 解得BC=31.5,∴线段BC 的长是31.5cm;
②如图(2),当点C 在线段AB 上时,
由线段的和差关系,得AD+CD+BC=AB,即 解得BC=4.5,∴线段BC 的长是4.5cm.
综上所述,BC的长是31.5cm 或4.5cm.
6.(2024·江苏扬州期末)如图,已知线段AB=12cm,点C为AB 上一点且AC=3cm,点 P 是BC的中点.
(1)求CP 的长度;
(2)点 D 是直线AB 上一点,且 CD+BD=13cm,求CD 的长.
解:(1)∵AB=12cm,AC=3cm,
∴BC=AB-AC=9 cm.
∵点 P 是BC 的中点,
(2)CD的长为2cm或11cm.
7.(2024·河北邢台期中)[新知理解]
点C 在线段AB 上,若 BC=2AC 或AC=2BC,则称点 C 是线段AB 的“优点”,线段AC,BC 称作互为“优点”伴侣线段.
例如,图(1)中线段AB 的长度为6,点C 在AB 上,AC 的长度为2,则点 C 是线段AB 的其中一个“优点”.
(1)若点 C 为图(1)中线段 AB 的“优点”,AC=6(AC(2)若点 D 也是图(1)中线段 AB 的“优点”(不同于点C),AC=6,则AC = BD(填“=”或“≠”);
[解决问题]
如图(2),数轴上有E,F两点,其中点 E 表示的数为1,点F 表示的数为4.
(3)若点 M 在点N 的左侧,且M,N均为线段OF 的“优点”,求线段 MN 的长;
(4)若点 G 在线段EF 的延长线上,且线段EF 与GF 互为“优点”伴侣线段,求点 G 表示的数.
解:(3)∵点F 表示的数为4,∴OF=4.当点 M 在点 N 左侧时,则 MF =2OM,ON=2NF,
∵OF=OM+MN+NF,∴MN=
(4)∵点E 表示的数为1,点F 表示的数为4,∴EF=4-1=3.
当线段 EF,GF 互为“优点”伴侣线段时,有EF=2GF或GF=2EF.
当EF=2GF 时,GF=1.5,∴点G 表示的数为5.5;
当GF=2EF 时,GF=6,∴点G 表示的数为10.综上所述,点G 表示的数为5.5 或10.
题型1数形结合思想
1.已知点 B,C在线段AD 上.
(1)如图,共有 条线段;
(2)如图,AB=CD.
①比较线段的大小:AC BD(填“>”“=”或“<”);
②若BD=4AB,BC=12cm,则 AD 的长为 cm;
(3)若AB:CD=1:2,且 E 为 BC 中点,求AE 与BD 的数量关系.(温馨提醒:重新画图)
题型2 整体思想
2.(2024·济南历下区二模)如图,C,D 是线段AB 上两点,且CD=3AD--2BC,则AC与BD 的数量关系是( ).
A. AC=BD B. 2AC=BD
C. 3AC=2BD D. 4AC=3BD
3.(1)如图,点 C 在线段AB 上,点 M 在线段AC上,点 N 在线段 BC 上.
①已知AC=13,CB=8,若点 M,N 分别是AC,BC 的中点,求线段 MN 的长;
②已知AC=13,CB=8,若点 M 是AC 的中点, 求线段MN 的长;
③已知AC=a,CB=b,若 请直接写出线段 MN 的长(用含a,b的式子表示);
(2)若点 C 在直线AB 上,(1)中其他条件不变,已知 3BN=2CN,请直接写出线段 MN 的长.
题型3 方程思想
4.(2023·湖南衡阳期末)如图是一个瓶子,已量得瓶塞AB 与标签CD 的高度之比为2:3,且标签底部 点C 是BD 的中点,又量得AE=330mm,求标签CD 的高度.
题型4 分类讨论思想
5.(2023·辽宁朝阳期末)点 C 在直线AB 上,点 D 为AC 的中点,如果 求线段 BC 的长.
6.(2024·江苏扬州期末)如图,已知线段AB=12cm,点C为AB 上一点且AC=3cm,点 P 是BC的中点.
(1)求CP 的长度;
(2)点 D 是直线AB 上一点,且 CD+BD=13cm,求CD 的长.
7.中考新考法 新定义问题(2024·河北邢台期中)[新知理解]
点 C 在线段AB 上,若 BC=2AC 或AC=2BC,则称点 C 是线段AB 的“优点”,线段AC,BC 称作互为“优点”伴侣线段.
例如,图(1)中线段AB 的长度为6,点C 在AB 上,AC 的长度为2,则点 C 是线段AB 的其中一个“优点”.
(1)若点 C 为图(1)中线段 AB 的“优点”,AC=6(AC
[解决问题]
如图(2),数轴上有 E,F两点,其中点 E 表示的数为1,点F 表示的数为4.
(3)若点 M 在点N 的左侧,且M,N均为线段OF 的“优点”,求线段 MN 的长;
(4)若点 G 在线段EF 的延长线上,且线段EF 与GF 互为“优点”伴侣线段,求点 G 表示的数.
中小学教育资源及组卷应用平台
题型1 数形结合思想
1.已知点 B,C在线段AD 上.
(1)如图,共有 6 条线段;
(2)如图,AB=CD.
①比较线段的大小:AC = BD(填“>”“=”或“<”);
②若BD=4AB,BC=12cm,则AD 的长为 20 cm;
(3)若AB:CD=1:2,且 E 为BC 中点,求AE 与BD 的数量关系.(温馨提醒:重新画图)
解:如图(1),当点C在AB的延长线上,
如图(2),当点C在线段AB上时,
题型2 整体思想
2.(2024·济南历下区二模)如图,C,D 是线段AB 上两点,且CD=3AD-2BC,则AC与BD 的数量关系是(C ).
A. AC=BD B. 2AC=BD
C. 3AC=2BD D. 4AC=3BD
3.(1)如图,点C 在线段AB 上,点 M 在线段AC上,点N 在线段BC上.
①已知AC=13,CB=8,若点 M,N 分别是AC,BC 的中点,求线段 MN 的长;
②已知AC=13,CB=8,若点 M 是AC 的中点, 求线段MN 的长;
③已知AC=a,CB=b,若 请直接写出线段 MN 的长(用含a,b的式子表示);
(2)若点 C 在直线AB 上,(1)中其他条件不变,已知 3BN=2CN,请直接写出线段MN 的长.
解:(1)①MN 的长为10.5.
②MN 的长为8.5.
(2)MN 的长为 或
题型3 方程思想
4.(2023·湖南衡阳期末)如图是一个瓶子,已量得瓶塞AB 与标签CD 的高度之比为2:3,且标签底部 点C 是BD的中点,又量得AE=330mm,求标签CD 的高度.
解:设DE的长为x mm.
∴AB=2DE=2x mm.
由AB:CD=2:3,AB=2x mm,得CD=3x mm.
∵点C 是BD 的中点,
∴BC=CD=3x mm.
∵AE=330 mm,∴AB+BC+CD+DE= 3x=110mm,
∴标签CD的高度为110mm.
题型4 分类讨论思想
5.(2023·辽宁朝阳期末)点C 在直线AB上,点 D 为AC 的中点,如果 求线段BC的长.
解:由 得
由D 是AC 的中点,得
①如图(1),当点C在线段AB 的延长线上时,
由线段的和差关系,得AD+CD-BC=AB,即 解得BC=31.5,∴线段BC 的长是31.5cm;
②如图(2),当点C 在线段AB 上时,
由线段的和差关系,得AD+CD+BC=AB,即 解得BC=4.5,∴线段BC 的长是4.5cm.
综上所述,BC的长是31.5cm 或4.5cm.
6.(2024·江苏扬州期末)如图,已知线段AB=12cm,点C为AB 上一点且AC=3cm,点 P 是BC的中点.
(1)求CP 的长度;
(2)点 D 是直线AB 上一点,且 CD+BD=13cm,求CD 的长.
解:(1)∵AB=12cm,AC=3cm,
∴BC=AB-AC=9 cm.
∵点 P 是BC 的中点,
(2)CD的长为2cm或11cm.
7.(2024·河北邢台期中)[新知理解]
点C 在线段AB 上,若 BC=2AC 或AC=2BC,则称点 C 是线段AB 的“优点”,线段AC,BC 称作互为“优点”伴侣线段.
例如,图(1)中线段AB 的长度为6,点C 在AB 上,AC 的长度为2,则点 C 是线段AB 的其中一个“优点”.
(1)若点 C 为图(1)中线段 AB 的“优点”,AC=6(AC
[解决问题]
如图(2),数轴上有E,F两点,其中点 E 表示的数为1,点F 表示的数为4.
(3)若点 M 在点N 的左侧,且M,N均为线段OF 的“优点”,求线段 MN 的长;
(4)若点 G 在线段EF 的延长线上,且线段EF 与GF 互为“优点”伴侣线段,求点 G 表示的数.
解:(3)∵点F 表示的数为4,∴OF=4.当点 M 在点 N 左侧时,则 MF =2OM,ON=2NF,
∵OF=OM+MN+NF,∴MN=
(4)∵点E 表示的数为1,点F 表示的数为4,∴EF=4-1=3.
当线段 EF,GF 互为“优点”伴侣线段时,有EF=2GF或GF=2EF.
当EF=2GF 时,GF=1.5,∴点G 表示的数为5.5;
当GF=2EF 时,GF=6,∴点G 表示的数为10.综上所述,点G 表示的数为5.5 或10.
同课章节目录
