6.3.3 余角和补角 同步提优训练(含答案) 2025-2026学年人教版七年级数学上册
文档属性
| 名称 | 6.3.3 余角和补角 同步提优训练(含答案) 2025-2026学年人教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 234.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 06:26:45 | ||
图片预览


文档简介
6.3.3 余角和补角
基础巩固提优
1.(2024·陕西西安期中)已知∠α与∠β互补,∠α与∠γ互余,若∠γ=30°,则∠β的度数为( ).
A. 30° B. 60° C. 120° D. 150°
2.(2022·连云港中考)已知∠A 的补角为 60°,则∠A= °.
3. 如图所示,已知∠AOC=2∠BOC,∠AOC 的余角比∠BOC 小30°.
(1)求∠AOC 的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD 的度数.
4.(2023·北京中考)如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC 的大小为( ).
A. 36° B. 44° C. 54° D. 63°
5.实验班原的 一副三角板按如图所示的方式摆放,则∠1的余角的度数为( ).
A. 45° B. 55° C. 65° D. 75°
6.(2024·山西太原期中)如图,将一副三角板(直角顶点重合)摆放在桌面上,此时∠AOC=∠BOD,得到此结论的依据是( ).
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等D.等角的补角相等
7.(2024·湖南长沙期末)如图,将一副三角尺按不同位置摆放,摆放方式中∠α=∠β的图形有( ).
A. 1个 B. 2个 C. 3个 D. 4个
8.教材P177练习T3·变式 已知一个角的补角是它的余角的4倍,则这个角的度数是( ).
A. 30° B. 45° C. 60° D. 67.5°
9.(2024·浙江台州期末)如图,∠AOB =∠COD=∠EOF=90°,则∠1,∠2,∠3 之间的数量关系为( ).
A. ∠1+∠2+∠3=90°
B. ∠1+∠2-∠3=90°
C. ∠2+∠3-∠1=90°
D. ∠1-∠2+∠3=90°
10.(2023·河北石家庄四十八中期末)按如图的方法折纸,下列说法不正确的是( ).
A. ∠1与∠3 互余
B. ∠2=90°
C. EA 平分∠BEF
D. ∠1与∠AEC 互补
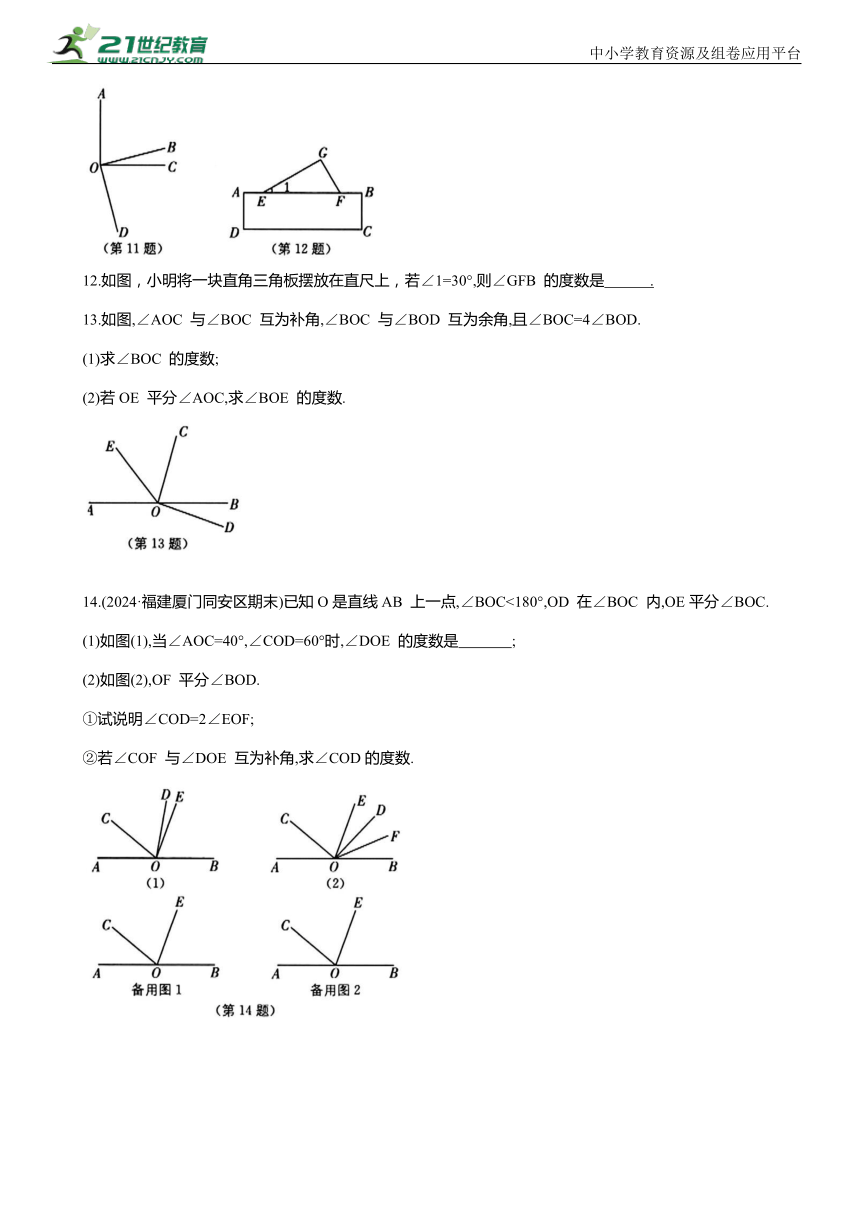
11.如图,射线OB,OC 在∠AOD 的内部,下列说法:①若∠AOC =∠BOD = 90°,则与∠BOC 互余的角有2个;②若∠AOD+∠BOC=180°,则∠AOC+∠BOD=180°;③若OM,ON 分别平分∠AOD,∠BOD,则. ④若∠AOD=150°,∠BOC=30°,作∠AOP= 则∠POQ=90°.其中正确的有( ).
A. 1个 B. 2 个 C. 3个 D. 4个
12.如图,小明将一块直角三角板摆放在直尺上,若∠1=30°,则∠GFB 的度数是 .
13.如图,∠AOC 与∠BOC 互为补角,∠BOC 与∠BOD 互为余角,且∠BOC=4∠BOD.
(1)求∠BOC 的度数;
(2)若OE 平分∠AOC,求∠BOE 的度数.
14.(2024·福建厦门同安区期末)已知O是直线AB 上一点,∠BOC<180°,OD 在∠BOC 内,OE平分∠BOC.
(1)如图(1),当∠AOC=40°,∠COD=60°时,∠DOE 的度数是 ;
(2)如图(2),OF 平分∠BOD.
①试说明∠COD=2∠EOF;
②若∠COF 与∠DOE 互为补角,求∠COD的度数.
中小学教育资源及组卷应用平台
6.3.3余角和补角
基础巩固提优
1.(2024·陕西西安期中)已知∠α与∠β互补,∠α与∠γ互余,若∠γ=30°,则∠β的度数为(C).
A. 30° B. 60° C. 120° D. 150°
2.(2022·连云港中考)已知∠A 的补角为 60°,则∠A= 120 °.
3.如图所示,已知∠AOC=2∠BOC,∠AOC 的余角比∠BOC 小30°.
(1)求∠AOC的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD 的度数.
解:(1)设∠BOC=x,
则∠AOC=2x,
依题意,得90°-2x=x-
30°,解得x=40°.
故
(2)由(1)得∠AOC=80°,
①当射线OD 在∠AOC 内部时,∠AOD=16°,则∠COD=∠AOC-∠AOD=80°-16°=64°;
②当射线OD 在∠AOC 外部时,∠AOD=16°,则.
思 维拓展提优 搭建综合应用与创新能力提升平台
4.(2023·北京中考)如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC 的大小为( C ).
A. 36° B. 44° C. 54° D. 63°
5.一副三角板按如图所示的方式摆放,则∠1的余角的度数为(D ).
A. 45° B. 55° C. 65° D. 75°
6.(2024·山西太原期中)如图,将一副三角板(直角顶点重合)摆放在桌面上,此时∠AOC=∠BOD,得到此结论的依据是(A).
A.同角的余角相等B.同角的补角相等
C.等角的余角相等D.等角的补角相等
7.(2024·湖南长沙期末)如图,将一副三角尺按不同位置摆放,摆放方式中∠α=∠β的图形有( C ).
A. 1个 B. 2 个 C. 3个 D. 4个
8.教材P177练习T3·变式 已知一个角的补角是它的余角的4倍,则这个角的度数是(C).
A. 30° B. 45° C. 60° D. 67.5°
9.(2024·浙江台州期末)如图,∠AOB=∠COD= ,则∠1,∠2,∠3 之间的数量关系为(D).
A. ∠1+∠2+∠3=90°
B. ∠1+∠2-∠3=90°
C. ∠2+∠3-∠1=90°
D. ∠1-∠2+∠3=90°
10.(2023·河北石家庄四十八中期末)按如图的方法折纸,下列说法不正确的是(C ).
A. ∠1与∠3 互余
B. ∠2=90°
C. EA 平分∠BEF
D. ∠1与∠AEC 互补
11.如图,射线 OB,OC 在∠AOD 的内部,下列说法:①若∠AOC =∠BOD = 90°,则与∠BOC 互余的角有2个;②若∠AOD+∠BOC=180°,则∠AOC+∠BOD=180°;③若OM,ON 分别平分∠AOD,∠BOD,则 ④若∠AOD=150°,∠BOC=30°,作∠AOP= 则∠POQ=90°.其中正确的有( C).
A. 1个 B. 2个 C. 3个 D.4个
12.如图,小明将一块直角三角板摆放在直尺上,若 ,则∠GFB 的度数是 120°.
13.如图,∠AOC 与∠BOC 互为补角,∠BOC 与∠BOD 互为余角,且∠BOC=4∠BOD.
(1)求∠BOC 的度数;
(2)若OE 平分∠AOC,求∠BOE 的度数.
解:(1)∵∠BOC 与∠BOD 互为余角,
∴∠BOC+∠BOD=90°.
∵∠BOC =4∠BOD,
(2)∵∠AOC 与∠BOC 互为补角,
∴∠AOC +∠BOC = 180°, ∴ ∠AOC =180°-∠BOC=180°-72°=108°.
∵OE 平分
14.(2024·福建厦门同安区期末)已知O 是直线AB 上一点,∠BOC<180°,OD 在∠BOC 内,OE平分∠BOC.
(1)如图(1),当∠AOC=40°,∠COD=60°时,∠DOE 的度数是 10° ;
(2)如图(2),OF 平分∠BOD.
①试说明∠COD=2∠EOF;
②若∠COF 与∠DOE 互为补角,求∠COD的度数.
解:①∵OE 平分∠BOC,
∴∠COE=∠BOE.
∵OF 平分∠BOD,∴∠DOF=∠BOF.
∵∠DOE=∠BOE-∠BOD,
∴∠DOE=∠COE-2∠DOF,
∴∠COD =∠COE +∠DOE = 2∠COE -2∠DOF.
∵∠EOF = ∠DOE + ∠DOF = ∠COE 2∠DOF+∠DOF=∠COE-∠DOF,
∴∠COD=2∠EOF.
②由①得∠COD=2∠COE-2∠DOF,∠DOE=∠COE-2∠DOF,
∴∠COF =∠COD +∠DOF =2∠COE-∠DOF,
∵∠COF 与∠DOE 互为补角,
∴∠COF+∠DOE=180°,
∴2∠COE-∠DOF+∠COE-2∠DOF=180°,
∴∠COE-∠DOF=60°,
∴∠COD=2∠COE-2∠DOF=120°.
基础巩固提优
1.(2024·陕西西安期中)已知∠α与∠β互补,∠α与∠γ互余,若∠γ=30°,则∠β的度数为( ).
A. 30° B. 60° C. 120° D. 150°
2.(2022·连云港中考)已知∠A 的补角为 60°,则∠A= °.
3. 如图所示,已知∠AOC=2∠BOC,∠AOC 的余角比∠BOC 小30°.
(1)求∠AOC 的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD 的度数.
4.(2023·北京中考)如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC 的大小为( ).
A. 36° B. 44° C. 54° D. 63°
5.实验班原的 一副三角板按如图所示的方式摆放,则∠1的余角的度数为( ).
A. 45° B. 55° C. 65° D. 75°
6.(2024·山西太原期中)如图,将一副三角板(直角顶点重合)摆放在桌面上,此时∠AOC=∠BOD,得到此结论的依据是( ).
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等D.等角的补角相等
7.(2024·湖南长沙期末)如图,将一副三角尺按不同位置摆放,摆放方式中∠α=∠β的图形有( ).
A. 1个 B. 2个 C. 3个 D. 4个
8.教材P177练习T3·变式 已知一个角的补角是它的余角的4倍,则这个角的度数是( ).
A. 30° B. 45° C. 60° D. 67.5°
9.(2024·浙江台州期末)如图,∠AOB =∠COD=∠EOF=90°,则∠1,∠2,∠3 之间的数量关系为( ).
A. ∠1+∠2+∠3=90°
B. ∠1+∠2-∠3=90°
C. ∠2+∠3-∠1=90°
D. ∠1-∠2+∠3=90°
10.(2023·河北石家庄四十八中期末)按如图的方法折纸,下列说法不正确的是( ).
A. ∠1与∠3 互余
B. ∠2=90°
C. EA 平分∠BEF
D. ∠1与∠AEC 互补
11.如图,射线OB,OC 在∠AOD 的内部,下列说法:①若∠AOC =∠BOD = 90°,则与∠BOC 互余的角有2个;②若∠AOD+∠BOC=180°,则∠AOC+∠BOD=180°;③若OM,ON 分别平分∠AOD,∠BOD,则. ④若∠AOD=150°,∠BOC=30°,作∠AOP= 则∠POQ=90°.其中正确的有( ).
A. 1个 B. 2 个 C. 3个 D. 4个
12.如图,小明将一块直角三角板摆放在直尺上,若∠1=30°,则∠GFB 的度数是 .
13.如图,∠AOC 与∠BOC 互为补角,∠BOC 与∠BOD 互为余角,且∠BOC=4∠BOD.
(1)求∠BOC 的度数;
(2)若OE 平分∠AOC,求∠BOE 的度数.
14.(2024·福建厦门同安区期末)已知O是直线AB 上一点,∠BOC<180°,OD 在∠BOC 内,OE平分∠BOC.
(1)如图(1),当∠AOC=40°,∠COD=60°时,∠DOE 的度数是 ;
(2)如图(2),OF 平分∠BOD.
①试说明∠COD=2∠EOF;
②若∠COF 与∠DOE 互为补角,求∠COD的度数.
中小学教育资源及组卷应用平台
6.3.3余角和补角
基础巩固提优
1.(2024·陕西西安期中)已知∠α与∠β互补,∠α与∠γ互余,若∠γ=30°,则∠β的度数为(C).
A. 30° B. 60° C. 120° D. 150°
2.(2022·连云港中考)已知∠A 的补角为 60°,则∠A= 120 °.
3.如图所示,已知∠AOC=2∠BOC,∠AOC 的余角比∠BOC 小30°.
(1)求∠AOC的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD 的度数.
解:(1)设∠BOC=x,
则∠AOC=2x,
依题意,得90°-2x=x-
30°,解得x=40°.
故
(2)由(1)得∠AOC=80°,
①当射线OD 在∠AOC 内部时,∠AOD=16°,则∠COD=∠AOC-∠AOD=80°-16°=64°;
②当射线OD 在∠AOC 外部时,∠AOD=16°,则.
思 维拓展提优 搭建综合应用与创新能力提升平台
4.(2023·北京中考)如图,∠AOC=∠BOD=90°,∠AOD=126°,则∠BOC 的大小为( C ).
A. 36° B. 44° C. 54° D. 63°
5.一副三角板按如图所示的方式摆放,则∠1的余角的度数为(D ).
A. 45° B. 55° C. 65° D. 75°
6.(2024·山西太原期中)如图,将一副三角板(直角顶点重合)摆放在桌面上,此时∠AOC=∠BOD,得到此结论的依据是(A).
A.同角的余角相等B.同角的补角相等
C.等角的余角相等D.等角的补角相等
7.(2024·湖南长沙期末)如图,将一副三角尺按不同位置摆放,摆放方式中∠α=∠β的图形有( C ).
A. 1个 B. 2 个 C. 3个 D. 4个
8.教材P177练习T3·变式 已知一个角的补角是它的余角的4倍,则这个角的度数是(C).
A. 30° B. 45° C. 60° D. 67.5°
9.(2024·浙江台州期末)如图,∠AOB=∠COD= ,则∠1,∠2,∠3 之间的数量关系为(D).
A. ∠1+∠2+∠3=90°
B. ∠1+∠2-∠3=90°
C. ∠2+∠3-∠1=90°
D. ∠1-∠2+∠3=90°
10.(2023·河北石家庄四十八中期末)按如图的方法折纸,下列说法不正确的是(C ).
A. ∠1与∠3 互余
B. ∠2=90°
C. EA 平分∠BEF
D. ∠1与∠AEC 互补
11.如图,射线 OB,OC 在∠AOD 的内部,下列说法:①若∠AOC =∠BOD = 90°,则与∠BOC 互余的角有2个;②若∠AOD+∠BOC=180°,则∠AOC+∠BOD=180°;③若OM,ON 分别平分∠AOD,∠BOD,则 ④若∠AOD=150°,∠BOC=30°,作∠AOP= 则∠POQ=90°.其中正确的有( C).
A. 1个 B. 2个 C. 3个 D.4个
12.如图,小明将一块直角三角板摆放在直尺上,若 ,则∠GFB 的度数是 120°.
13.如图,∠AOC 与∠BOC 互为补角,∠BOC 与∠BOD 互为余角,且∠BOC=4∠BOD.
(1)求∠BOC 的度数;
(2)若OE 平分∠AOC,求∠BOE 的度数.
解:(1)∵∠BOC 与∠BOD 互为余角,
∴∠BOC+∠BOD=90°.
∵∠BOC =4∠BOD,
(2)∵∠AOC 与∠BOC 互为补角,
∴∠AOC +∠BOC = 180°, ∴ ∠AOC =180°-∠BOC=180°-72°=108°.
∵OE 平分
14.(2024·福建厦门同安区期末)已知O 是直线AB 上一点,∠BOC<180°,OD 在∠BOC 内,OE平分∠BOC.
(1)如图(1),当∠AOC=40°,∠COD=60°时,∠DOE 的度数是 10° ;
(2)如图(2),OF 平分∠BOD.
①试说明∠COD=2∠EOF;
②若∠COF 与∠DOE 互为补角,求∠COD的度数.
解:①∵OE 平分∠BOC,
∴∠COE=∠BOE.
∵OF 平分∠BOD,∴∠DOF=∠BOF.
∵∠DOE=∠BOE-∠BOD,
∴∠DOE=∠COE-2∠DOF,
∴∠COD =∠COE +∠DOE = 2∠COE -2∠DOF.
∵∠EOF = ∠DOE + ∠DOF = ∠COE 2∠DOF+∠DOF=∠COE-∠DOF,
∴∠COD=2∠EOF.
②由①得∠COD=2∠COE-2∠DOF,∠DOE=∠COE-2∠DOF,
∴∠COF =∠COD +∠DOF =2∠COE-∠DOF,
∵∠COF 与∠DOE 互为补角,
∴∠COF+∠DOE=180°,
∴2∠COE-∠DOF+∠COE-2∠DOF=180°,
∴∠COE-∠DOF=60°,
∴∠COD=2∠COE-2∠DOF=120°.
同课章节目录
