6.1~6.3 阶段巩固检测(含答案)2025-2026学年人教版七年级数学上册
文档属性
| 名称 | 6.1~6.3 阶段巩固检测(含答案)2025-2026学年人教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 413.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 06:23:59 | ||
图片预览




文档简介
6.1~6.3阶段巩固检测
题型1 从不同方向看立体图形
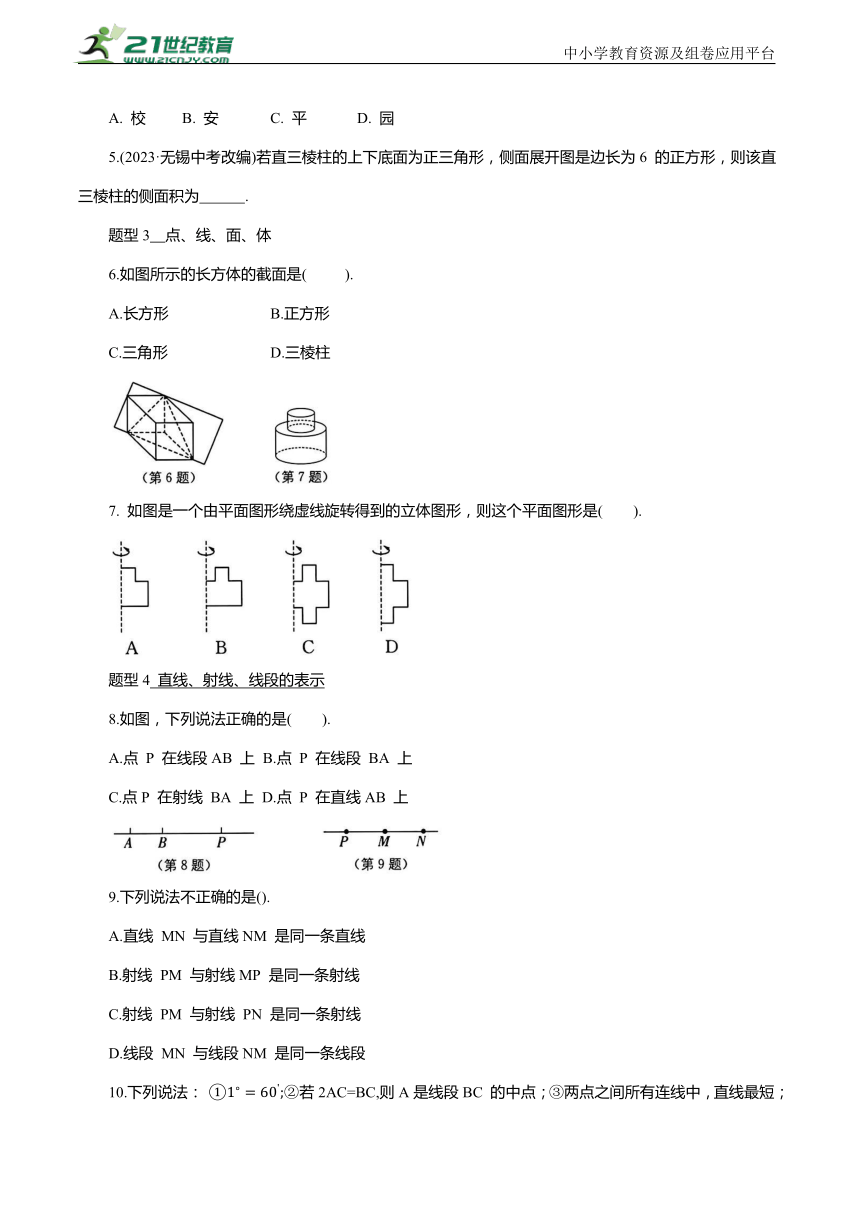
1.(2024·江西中考改编)如图所示的几何体,其从前面看为( ).
2.(2023·安徽中考改编)某几何体从前面、左面和上面看到的平面图形如图所示,则该几何体为( ).
题型2 平面展开图
3.(2024·太原二模)一个棱柱的侧面展开图如图所示,则该棱柱底面的形状是( ).
4.(2024·广安中考)将“共建平安校园”六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体上,与“共”字所在面相对的面上的汉字是( ).
A. 校 B. 安 C. 平 D. 园
5.(2023·无锡中考改编)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6 的正方形,则该直三棱柱的侧面积为 .
题型3 点、线、面、体
6.如图所示的长方体的截面是( ).
A.长方形 B.正方形
C.三角形 D.三棱柱
7. 如图是一个由平面图形绕虚线旋转得到的立体图形,则这个平面图形是( ).
题型4 直线、射线、线段的表示
8.如图,下列说法正确的是( ).
A.点 P 在线段AB 上 B.点 P 在线段 BA 上
C.点P 在射线 BA 上 D.点 P 在直线AB 上
9.下列说法不正确的是().
A.直线 MN 与直线NM 是同一条直线
B.射线 PM 与射线MP 是同一条射线
C.射线 PM 与射线 PN 是同一条射线
D.线段 MN 与线段NM 是同一条线段
10.下列说法: ②若2AC=BC,则A是线段BC 的中点;③两点之间所有连线中,直线最短;④两点确定一条直线.其中正确的有( ).
A. ②③④ B. ①②③
C. ①②④ D. ①④
题型5 线段的有关计算
11.在线段AB上,M 为AC的中点,N 为DB 的中点,AB=a,CD=b,MN 的长为( ).
12.两根木条,一根长8cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( ).
A. 2cm B. 10cm
C. 1 cm或11 cm D. 2cm或 10cm
13.(2024·重庆北碚区期中)如图,A,B,C,D 在同一直线上,已知 点 E,点 F 分别是AC,BD 的中点,若 EF=3,则CD= .
14.已知线段 AB 如图所示,延长 AB 至C,使BC=AB,反向延长AB至D,使AD=3AB.点 M 是CD的中点,点 N 是AD 的中点.
(1)依题意补全图形;
(2)若MN 的长为2,求线段CD 的长度.
题型6 角的度分秒的互化与运算
度 分 秒.
16.计算:
17.计算:
18.下列度分秒运算中,正确的是( ).
(精确到分)
题型7 角的和差倍分与角的平分线
19.如图,点O 是直线 AB 上一点,∠COD=50°,OE,OF 分别平分∠AOC 和∠DOB,求∠EOF的度数.
题型8 余角、补角及其性质
20.(2024·浙江绍兴期末)如果∠α 和∠β互补,且∠α<∠β,下列表示∠α的余角的式子中,其中不正确的是( ).
A. 90°-∠α B. ∠β—90°
C. 180°-∠β
21.(2024·江苏盐城期末)如图,已知∠AOB.
(1)试用量角器或三角尺在 OB 的下方画∠AOB 的余角∠BOC;
(2)画射线OB 的反向延长线OD,若∠COD=115°,求∠AOB 的度数.
题型9 方位角
22.如图,下列说法中错误的是( ).
A. OA 的方向是东北方向
B. OB 的方向是北偏西60°
C. OC 的方向是南偏西60°
D. OD 的方向是南偏东60°
23.(2023·河南驻马店期末)学校、电影院、公园在平面图上的标点分别是A,B,C,电影院在学校的正东方向,公园在学校的南偏西 25°方向,那么平面图上的∠CAB 等于( ).
A. 115°B. 155° C. 25° D. 65°
24.如图,在点O 的北偏东 60°的某处有一点A,∠AOE 与∠BOW 互余,OC 平分∠AOB.
(1) ∠AOE 和 ∠BOW 的 数 量 关 系 是 ;
(2)请通过计算说明射线 OC 和OB 的方向.
25.将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图(1),若∠AOB=155°,求∠AOD,∠BOC,∠DOC 的度数.
(2)如图(1),你发现∠AOD 与∠BOC 的大小有何关系 ∠AOB 与∠DOC 有何关系 直接写出你发现的结论.
(3)如图(2),当△AOC 与△BOD 没有重合部分时,(2)中你发现的结论是否还仍然成立 请说明理由.
26.(2023·福建三明永安期中)如图是一个几何体从三个方向看所得到的形状图.
(1)画出这个几何体,并写出它的名称;
(2)画出它的一种平面展开图;
(3)若从前面看的高为3cm,从上面看三角形的边长为2cm,求这个几何体的侧面积.
27.(2023·辽宁抚顺望花区期末)已知∠AOB 与∠BOC互为补角,OD 平分∠BOC.
(1)如图(1),若∠AOB=80°,则∠BOC= °,∠AOD= °;
(2)如图(2),若∠AOB=140°,求∠AOD 的度数;
(3)若∠AOB=n°,直接写出∠AOD 的度数(用含 n的代数式表示)及相应的 n 的取值范围.
28.(2024·江苏徐州期中)[新知理解]
如图(1),点C 在线段AB 上,若 BC=πAC,则称点 C 是线段AB 的圆周率点,线段AC,BC 称作互为圆周率伴侣线段.
(1)若AC=3,则AB= ;
(2)若点 D 也是图(1)中线段 AB 的圆周率点(不同于点C),则AC BD;(填“=”或“≠”)
[解决问题]
如图(2),现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1 的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C 的位置.
(3)若点 M,N 是线段OC 的圆周率点,则MN 的长为 ;
(4)图(2)中,若点 D 在射线OC 上,且线段CD 与以O,C,D中某两个点为端点的线段互为圆周率伴侣线段,请直接写出点 D 所表示的数.
题型1 从不同方向看立体图形
1.(2024·江西中考改编)如图所示的几何体,其从前面看为( B).
2.(2023·安徽中考改编)某几何体从前面、左面和上面看到的平面图形如图所示,则该几何体为( B ).
题型2 平面展开图
3.(2024·太原二模)一个棱柱的侧面展开图如图所示,则该棱柱底面的形状是(B).
4.(2024·广安中考)将“共建平安校园”六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体上,与“共”字所在面相对的面上的汉字是(A).
A. 校 B. 安 C. 平 D. 园
5.(2023·无锡中考改编)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的侧面积为 36 .
题型3 点、线、面、体
6.如图所示的长方体的截面是(C).
A.长方形 B. 正方形
C.三角形 D. 三棱柱
7.如图是一个由平面图形绕虚线旋转得到的立体图形,则这个平面图形是(A).
题型4 直线、射线、线段的表示
8.如图,下列说法正确的是( D).
A.点 P 在线段AB上 B.点 P 在线段BA 上
C.点P 在射线BA 上 D.点 P 在直线AB 上
9.下列说法不正确的是( B ).
A.直线 MN 与直线NM 是同一条直线
B.射线 PM 与射线MP 是同一条射线
C.射线 PM 与射线 PN 是同一条射线
D.线段MN 与线段NM 是同一条线段
10.下列说法:( ②若2AC=BC,则A是线段BC 的中点;③两点之间所有连线中,直线最短;④两点确定一条直线.其中正确的有( D).
A. ②③④ B. ①②③
C. ①②④ D. ①④
题型5 线段的有关计算
11.在线段AB 上,M为AC的中点,N 为DB 的中点,AB=a,CD=b,MN的长为( D).
12.两根木条,一根长8cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为(D).
A. 2cm B. 10cm
C. 1 cm或11cm D. 2cm或10cm
13.(2024·重庆北碚区期中)如图,A,B,C,D 在同一直线上,已知 点E,点 F 分别是AC,BD 的中点,若EF=3,则CD= 5 .
14.已知线段AB 如图所示,延长 AB 至C,使BC=AB,反向延长AB至D,使AD=3AB.点 M 是CD 的中点,点 N 是AD 的中点.
(1)依题意补全图形;
(2)若MN 的长为2,求线段CD 的长度.
(第1题)
解:(1)如图所示.
(2)∵AD=3AB,设AB=x,则 BC=x,AD=3x,∴CD=CB+BA+AD=5x.
∵点M是CD 的中点,点N 是AD 的中点,
解得x=2,∴CD=5x=10.
故线段CD的长度为10.
题型6 角的度分秒的互化与运算
度 28 分 48 秒.
16.计算:
17.计算:
18.下列度分秒运算中,正确的是(D).
(精确到分)
题型7 角的和差倍分与角的平分线
19.如图,点O 是直线AB 上一点,∠COD=50°,OE,OF 分别平分∠AOC 和∠DOB,求∠EOF的度数.
解:因为∠COD=50°,所以∠AOC+∠BOD
因为OE ,OF 分别平分∠AOC 和∠DOB,所以∠AOE=∠COE,∠DOF=∠BOF,所以 =65°,所以∠EOF =∠EOC +∠DOF +
题型8 余角、补角及其性质
20.(2024·浙江绍兴期末)如果∠α 和∠β互补,且∠α<∠β,下列表示∠α的余角的式子中,其中不正确的是( C).
A. 90°-∠α B. ∠β-90°
21.(2024·江苏盐城期末)如图,已知∠AOB.
(1)试用量角器或三角尺在 OB 的下方画∠AOB 的余角∠BOC;
中小学教育资源及组卷应用平台
(2)画射线OB 的反向延长线OD,若∠COD=115°,求∠AOB 的度数.
解:(1)如图所示,∠BOC 即为所求.
(2)如图,OD 即为所求.
∵∠COD=115°,
∴∠BOC=180°-∠COD=65°.
=∠AOC-∠BOC=25°.
题型9 方位角
22.如图,下列说法中错误的是(D).
A. OA 的方向是东北方向
B. OB 的方向是北偏西60°
C. OC 的方向是南偏西60°
D. OD 的方向是南偏东60°
23.(2023·河南驻马店期末)学校、电影院、公园在平面图上的标点分别是A,B,C,电影院在学校的正东方向,公园在学校的南偏西25°方向,那么平面图上的∠CAB 等于(A).
A. 115°B. 155° C. 25° D. 65°
24.如图,在点O 的北偏东60°的某处有一点 A,∠AOE 与∠BOW 互余,OC 平分∠AOB.
(1) ∠AOE 和 ∠BOW 的 数 量 关 系 是∠AOE+∠BOW=90°;
(2)请通过计算说明射线OC 和OB 的方向.
解:根据题意,得∠NOA=60°,∠NOE=∠NOW=90°,∴∠AOE=∠NOE
又∠AOE+∠BOW=90°,∴∠BOW=60°,
∴∠NOB=∠NOW-∠BOW=90°-60°=30°,∴射线OB 的方向是北偏西30°方向.
∵OC 平分∠AOB,∠AOB=∠BON+∠NOA
∴∠NOC=∠NOA-∠COA =60°-45°=15°,∴射线OC 的方向是北偏东15°方向.
思维拓展 搭建综合应用与创新能力提升平台
25.将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图(1),若∠AOB=155°,求∠AOD,∠BOC,∠DOC 的度数.
(2)如图(1),你发现∠AOD 与∠BOC 的大小有何关系 ∠AOB 与∠DOC 有何关系 直接写出你发现的结论.
(3)如图(2),当△AOC 与△BOD 没有重合部分时,(2)中你发现的结论是否还仍然成立 请说明理由.
解:(1)∵∠AOB=155°,∠AOC=∠BOD=90°,∴∠AOD=∠BOC=155°-90°=65°,∠DOC=∠BOD-∠BOC=90°-65°=25°.
(2)∠AOD=∠BOC,∠AOB+∠DOC=180°.
(3)仍然成立.理由如下:
∵∠AOC=∠BOD=90°,∴∠AOC+∠COD=∠BOD+∠COD,即∠AOD=∠BOC.
又∠AOB +∠COD +∠AOC+∠BOD=360°,∴∠AOB+∠DOC=180°.
26.(2023·福建三明永安期中)如图是一个几何体从三个方向看所得到的形状图.
(1)画出这个几何体,并写出它的名称;
(2)画出它的一种平面展开图;
(3)若从前面看的高为3cm,从上面看三角形的边长为2cm,求这个几何体的侧面积.
解:(1)根据这个几何体从三个方向看所得到的形状图判断,该几何体是正三棱柱(如图(1)).
(2)它的一种平面展开图如图(2)所示.
(3)∵正三棱柱的底面边长为2cm,侧棱长是3cm,∴其侧面积是(3×2)×3=6×3=18(cm ).
27.(2023·辽宁抚顺望花区期末)已知∠AOB 与∠BOC互为补角,OD 平分∠BOC.
(1)如图(1),若∠AOB=80°,则∠BOC= 100 °,∠AOD= 130 °;
(2)如图(2),若∠AOB=140°,求∠AOD 的度数;
(3)若∠AOB=n°,直接写出∠AOD 的度数(用含 n的代数式表示)及相应的 n的取值范围.
解:(2)∠AOD 的度数为 160°或120°.
(3)当 OC 和 OA 在 OB 的不同侧时, 当OC 和OA 在 OB 的同一侧时,当 n = 60 时, ;当028.(2024·江苏徐州期中)[新知理解]
如图(1),点C 在线段AB 上,若BC=πAC,则称点 C 是线段AB 的圆周率点,线段AC,BC 称作互为圆周率伴侣线段.
(1)若AC=3,则AB= 3+3π ;
(2)若点 D 也是图(1)中线段 AB 的圆周率点(不同于点C),则AC = BD;(填“=”或“≠”)
[解决问题]
如图(2),现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1 的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点 C 的位置.
(3)若点 M,N 是线段OC 的圆周率点,则MN 的长为 0或π-1 ;
(4)图(2)中,若点 D 在射线OC 上,且线段CD 与以O,C,D中某两个点为端点的线段互为圆周率伴侣线段,请直接写出点 D 所表示的数.
解:点D 所表示的数为1或π或2+ 或
题型1 从不同方向看立体图形
1.(2024·江西中考改编)如图所示的几何体,其从前面看为( ).
2.(2023·安徽中考改编)某几何体从前面、左面和上面看到的平面图形如图所示,则该几何体为( ).
题型2 平面展开图
3.(2024·太原二模)一个棱柱的侧面展开图如图所示,则该棱柱底面的形状是( ).
4.(2024·广安中考)将“共建平安校园”六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体上,与“共”字所在面相对的面上的汉字是( ).
A. 校 B. 安 C. 平 D. 园
5.(2023·无锡中考改编)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6 的正方形,则该直三棱柱的侧面积为 .
题型3 点、线、面、体
6.如图所示的长方体的截面是( ).
A.长方形 B.正方形
C.三角形 D.三棱柱
7. 如图是一个由平面图形绕虚线旋转得到的立体图形,则这个平面图形是( ).
题型4 直线、射线、线段的表示
8.如图,下列说法正确的是( ).
A.点 P 在线段AB 上 B.点 P 在线段 BA 上
C.点P 在射线 BA 上 D.点 P 在直线AB 上
9.下列说法不正确的是().
A.直线 MN 与直线NM 是同一条直线
B.射线 PM 与射线MP 是同一条射线
C.射线 PM 与射线 PN 是同一条射线
D.线段 MN 与线段NM 是同一条线段
10.下列说法: ②若2AC=BC,则A是线段BC 的中点;③两点之间所有连线中,直线最短;④两点确定一条直线.其中正确的有( ).
A. ②③④ B. ①②③
C. ①②④ D. ①④
题型5 线段的有关计算
11.在线段AB上,M 为AC的中点,N 为DB 的中点,AB=a,CD=b,MN 的长为( ).
12.两根木条,一根长8cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( ).
A. 2cm B. 10cm
C. 1 cm或11 cm D. 2cm或 10cm
13.(2024·重庆北碚区期中)如图,A,B,C,D 在同一直线上,已知 点 E,点 F 分别是AC,BD 的中点,若 EF=3,则CD= .
14.已知线段 AB 如图所示,延长 AB 至C,使BC=AB,反向延长AB至D,使AD=3AB.点 M 是CD的中点,点 N 是AD 的中点.
(1)依题意补全图形;
(2)若MN 的长为2,求线段CD 的长度.
题型6 角的度分秒的互化与运算
度 分 秒.
16.计算:
17.计算:
18.下列度分秒运算中,正确的是( ).
(精确到分)
题型7 角的和差倍分与角的平分线
19.如图,点O 是直线 AB 上一点,∠COD=50°,OE,OF 分别平分∠AOC 和∠DOB,求∠EOF的度数.
题型8 余角、补角及其性质
20.(2024·浙江绍兴期末)如果∠α 和∠β互补,且∠α<∠β,下列表示∠α的余角的式子中,其中不正确的是( ).
A. 90°-∠α B. ∠β—90°
C. 180°-∠β
21.(2024·江苏盐城期末)如图,已知∠AOB.
(1)试用量角器或三角尺在 OB 的下方画∠AOB 的余角∠BOC;
(2)画射线OB 的反向延长线OD,若∠COD=115°,求∠AOB 的度数.
题型9 方位角
22.如图,下列说法中错误的是( ).
A. OA 的方向是东北方向
B. OB 的方向是北偏西60°
C. OC 的方向是南偏西60°
D. OD 的方向是南偏东60°
23.(2023·河南驻马店期末)学校、电影院、公园在平面图上的标点分别是A,B,C,电影院在学校的正东方向,公园在学校的南偏西 25°方向,那么平面图上的∠CAB 等于( ).
A. 115°B. 155° C. 25° D. 65°
24.如图,在点O 的北偏东 60°的某处有一点A,∠AOE 与∠BOW 互余,OC 平分∠AOB.
(1) ∠AOE 和 ∠BOW 的 数 量 关 系 是 ;
(2)请通过计算说明射线 OC 和OB 的方向.
25.将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图(1),若∠AOB=155°,求∠AOD,∠BOC,∠DOC 的度数.
(2)如图(1),你发现∠AOD 与∠BOC 的大小有何关系 ∠AOB 与∠DOC 有何关系 直接写出你发现的结论.
(3)如图(2),当△AOC 与△BOD 没有重合部分时,(2)中你发现的结论是否还仍然成立 请说明理由.
26.(2023·福建三明永安期中)如图是一个几何体从三个方向看所得到的形状图.
(1)画出这个几何体,并写出它的名称;
(2)画出它的一种平面展开图;
(3)若从前面看的高为3cm,从上面看三角形的边长为2cm,求这个几何体的侧面积.
27.(2023·辽宁抚顺望花区期末)已知∠AOB 与∠BOC互为补角,OD 平分∠BOC.
(1)如图(1),若∠AOB=80°,则∠BOC= °,∠AOD= °;
(2)如图(2),若∠AOB=140°,求∠AOD 的度数;
(3)若∠AOB=n°,直接写出∠AOD 的度数(用含 n的代数式表示)及相应的 n 的取值范围.
28.(2024·江苏徐州期中)[新知理解]
如图(1),点C 在线段AB 上,若 BC=πAC,则称点 C 是线段AB 的圆周率点,线段AC,BC 称作互为圆周率伴侣线段.
(1)若AC=3,则AB= ;
(2)若点 D 也是图(1)中线段 AB 的圆周率点(不同于点C),则AC BD;(填“=”或“≠”)
[解决问题]
如图(2),现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1 的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C 的位置.
(3)若点 M,N 是线段OC 的圆周率点,则MN 的长为 ;
(4)图(2)中,若点 D 在射线OC 上,且线段CD 与以O,C,D中某两个点为端点的线段互为圆周率伴侣线段,请直接写出点 D 所表示的数.
题型1 从不同方向看立体图形
1.(2024·江西中考改编)如图所示的几何体,其从前面看为( B).
2.(2023·安徽中考改编)某几何体从前面、左面和上面看到的平面图形如图所示,则该几何体为( B ).
题型2 平面展开图
3.(2024·太原二模)一个棱柱的侧面展开图如图所示,则该棱柱底面的形状是(B).
4.(2024·广安中考)将“共建平安校园”六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体上,与“共”字所在面相对的面上的汉字是(A).
A. 校 B. 安 C. 平 D. 园
5.(2023·无锡中考改编)若直三棱柱的上下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的侧面积为 36 .
题型3 点、线、面、体
6.如图所示的长方体的截面是(C).
A.长方形 B. 正方形
C.三角形 D. 三棱柱
7.如图是一个由平面图形绕虚线旋转得到的立体图形,则这个平面图形是(A).
题型4 直线、射线、线段的表示
8.如图,下列说法正确的是( D).
A.点 P 在线段AB上 B.点 P 在线段BA 上
C.点P 在射线BA 上 D.点 P 在直线AB 上
9.下列说法不正确的是( B ).
A.直线 MN 与直线NM 是同一条直线
B.射线 PM 与射线MP 是同一条射线
C.射线 PM 与射线 PN 是同一条射线
D.线段MN 与线段NM 是同一条线段
10.下列说法:( ②若2AC=BC,则A是线段BC 的中点;③两点之间所有连线中,直线最短;④两点确定一条直线.其中正确的有( D).
A. ②③④ B. ①②③
C. ①②④ D. ①④
题型5 线段的有关计算
11.在线段AB 上,M为AC的中点,N 为DB 的中点,AB=a,CD=b,MN的长为( D).
12.两根木条,一根长8cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为(D).
A. 2cm B. 10cm
C. 1 cm或11cm D. 2cm或10cm
13.(2024·重庆北碚区期中)如图,A,B,C,D 在同一直线上,已知 点E,点 F 分别是AC,BD 的中点,若EF=3,则CD= 5 .
14.已知线段AB 如图所示,延长 AB 至C,使BC=AB,反向延长AB至D,使AD=3AB.点 M 是CD 的中点,点 N 是AD 的中点.
(1)依题意补全图形;
(2)若MN 的长为2,求线段CD 的长度.
(第1题)
解:(1)如图所示.
(2)∵AD=3AB,设AB=x,则 BC=x,AD=3x,∴CD=CB+BA+AD=5x.
∵点M是CD 的中点,点N 是AD 的中点,
解得x=2,∴CD=5x=10.
故线段CD的长度为10.
题型6 角的度分秒的互化与运算
度 28 分 48 秒.
16.计算:
17.计算:
18.下列度分秒运算中,正确的是(D).
(精确到分)
题型7 角的和差倍分与角的平分线
19.如图,点O 是直线AB 上一点,∠COD=50°,OE,OF 分别平分∠AOC 和∠DOB,求∠EOF的度数.
解:因为∠COD=50°,所以∠AOC+∠BOD
因为OE ,OF 分别平分∠AOC 和∠DOB,所以∠AOE=∠COE,∠DOF=∠BOF,所以 =65°,所以∠EOF =∠EOC +∠DOF +
题型8 余角、补角及其性质
20.(2024·浙江绍兴期末)如果∠α 和∠β互补,且∠α<∠β,下列表示∠α的余角的式子中,其中不正确的是( C).
A. 90°-∠α B. ∠β-90°
21.(2024·江苏盐城期末)如图,已知∠AOB.
(1)试用量角器或三角尺在 OB 的下方画∠AOB 的余角∠BOC;
中小学教育资源及组卷应用平台
(2)画射线OB 的反向延长线OD,若∠COD=115°,求∠AOB 的度数.
解:(1)如图所示,∠BOC 即为所求.
(2)如图,OD 即为所求.
∵∠COD=115°,
∴∠BOC=180°-∠COD=65°.
=∠AOC-∠BOC=25°.
题型9 方位角
22.如图,下列说法中错误的是(D).
A. OA 的方向是东北方向
B. OB 的方向是北偏西60°
C. OC 的方向是南偏西60°
D. OD 的方向是南偏东60°
23.(2023·河南驻马店期末)学校、电影院、公园在平面图上的标点分别是A,B,C,电影院在学校的正东方向,公园在学校的南偏西25°方向,那么平面图上的∠CAB 等于(A).
A. 115°B. 155° C. 25° D. 65°
24.如图,在点O 的北偏东60°的某处有一点 A,∠AOE 与∠BOW 互余,OC 平分∠AOB.
(1) ∠AOE 和 ∠BOW 的 数 量 关 系 是∠AOE+∠BOW=90°;
(2)请通过计算说明射线OC 和OB 的方向.
解:根据题意,得∠NOA=60°,∠NOE=∠NOW=90°,∴∠AOE=∠NOE
又∠AOE+∠BOW=90°,∴∠BOW=60°,
∴∠NOB=∠NOW-∠BOW=90°-60°=30°,∴射线OB 的方向是北偏西30°方向.
∵OC 平分∠AOB,∠AOB=∠BON+∠NOA
∴∠NOC=∠NOA-∠COA =60°-45°=15°,∴射线OC 的方向是北偏东15°方向.
思维拓展 搭建综合应用与创新能力提升平台
25.将一副三角板放在同一平面内,使直角顶点重合于点O.
(1)如图(1),若∠AOB=155°,求∠AOD,∠BOC,∠DOC 的度数.
(2)如图(1),你发现∠AOD 与∠BOC 的大小有何关系 ∠AOB 与∠DOC 有何关系 直接写出你发现的结论.
(3)如图(2),当△AOC 与△BOD 没有重合部分时,(2)中你发现的结论是否还仍然成立 请说明理由.
解:(1)∵∠AOB=155°,∠AOC=∠BOD=90°,∴∠AOD=∠BOC=155°-90°=65°,∠DOC=∠BOD-∠BOC=90°-65°=25°.
(2)∠AOD=∠BOC,∠AOB+∠DOC=180°.
(3)仍然成立.理由如下:
∵∠AOC=∠BOD=90°,∴∠AOC+∠COD=∠BOD+∠COD,即∠AOD=∠BOC.
又∠AOB +∠COD +∠AOC+∠BOD=360°,∴∠AOB+∠DOC=180°.
26.(2023·福建三明永安期中)如图是一个几何体从三个方向看所得到的形状图.
(1)画出这个几何体,并写出它的名称;
(2)画出它的一种平面展开图;
(3)若从前面看的高为3cm,从上面看三角形的边长为2cm,求这个几何体的侧面积.
解:(1)根据这个几何体从三个方向看所得到的形状图判断,该几何体是正三棱柱(如图(1)).
(2)它的一种平面展开图如图(2)所示.
(3)∵正三棱柱的底面边长为2cm,侧棱长是3cm,∴其侧面积是(3×2)×3=6×3=18(cm ).
27.(2023·辽宁抚顺望花区期末)已知∠AOB 与∠BOC互为补角,OD 平分∠BOC.
(1)如图(1),若∠AOB=80°,则∠BOC= 100 °,∠AOD= 130 °;
(2)如图(2),若∠AOB=140°,求∠AOD 的度数;
(3)若∠AOB=n°,直接写出∠AOD 的度数(用含 n的代数式表示)及相应的 n的取值范围.
解:(2)∠AOD 的度数为 160°或120°.
(3)当 OC 和 OA 在 OB 的不同侧时, 当OC 和OA 在 OB 的同一侧时,当 n = 60 时, ;当0
如图(1),点C 在线段AB 上,若BC=πAC,则称点 C 是线段AB 的圆周率点,线段AC,BC 称作互为圆周率伴侣线段.
(1)若AC=3,则AB= 3+3π ;
(2)若点 D 也是图(1)中线段 AB 的圆周率点(不同于点C),则AC = BD;(填“=”或“≠”)
[解决问题]
如图(2),现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1 的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点 C 的位置.
(3)若点 M,N 是线段OC 的圆周率点,则MN 的长为 0或π-1 ;
(4)图(2)中,若点 D 在射线OC 上,且线段CD 与以O,C,D中某两个点为端点的线段互为圆周率伴侣线段,请直接写出点 D 所表示的数.
解:点D 所表示的数为1或π或2+ 或
同课章节目录
