21.3 实际问题与一元二次方程 同步提优训练(含解析) 2025-2026学年人教版九年级数学上册
文档属性
| 名称 | 21.3 实际问题与一元二次方程 同步提优训练(含解析) 2025-2026学年人教版九年级数学上册 |  | |
| 格式 | |||
| 文件大小 | 840.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 11:33:58 | ||
图片预览


文档简介
21.3实际问题与一元二次方程
一、单选题
1.庆“元旦”,市工会组织篮球比赛,赛制分为主场、客场交替进行,共进行了 72 场比赛,若设这
次有 x 队参加比赛,则根据题意可列方程为( )
1
A. x(x+1)=72 B.x(x+1)=72
2
1
C. x(x-1)=72 D.x(x-1)=72
2
2.某厂家 2024 年 1~5 月份销售的电车数量如图所示.设从 2 月份到 4 月份,该厂家电车销售的平
均月增长率为 ,根据题意可得方程( )
A.140(1 )2 = 461 B.180(1 + )2 = 461
C.450(1 )2 = 368 D.368(1 + )2 = 450
3.某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛 28 场,则参加此次比赛
的球队数是( )
A.6 B.7 C.8 D.9
4.北京奥运会的主会场“鸟巢”让人记忆深刻.在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结构
用钢量从 5.4 万吨减少到 4.2 万吨.若设平均每次用钢量降低的百分率为 x,根据题意,可得方程
( )
A.5.4(1﹣x)2=4.2 B.5.4(1﹣x2)=4.2
C.5.4(1﹣2x)=4.2 D.4.2(1+x)2=5.4
5.在某次同学聚会上,每两个人都握一次手,所有人共握手 45 次,设有 x 人参加这次聚会,则列
出方程正确的是( )
A.x(x+1)=45 B.x(x﹣1)=45
C. =45 D. =45
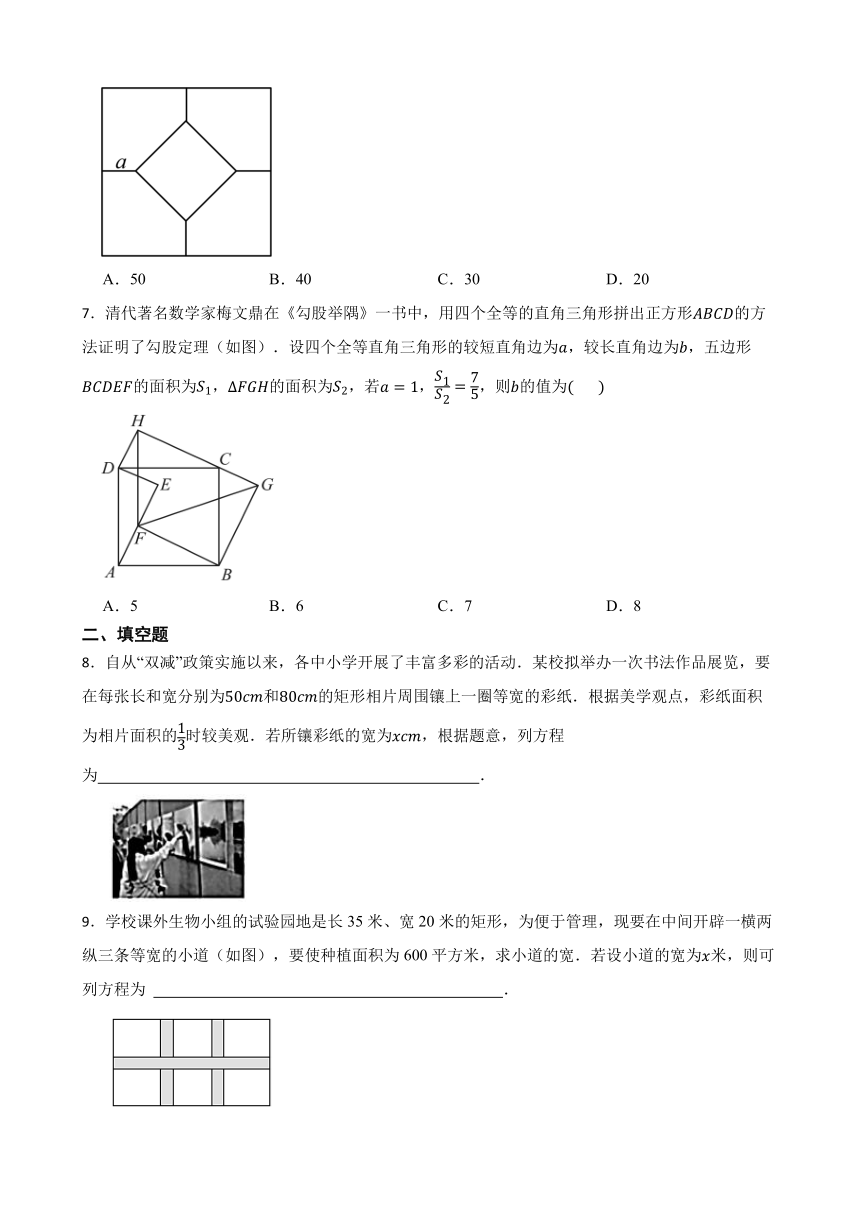
6.如图,一块正方形地砖的图案是由 4 个全等的五边形和 1 个小正方形组成的,已知小正方形的面
积和五边形的面积相等,并且图中线段 a 的长度为√10 2,则这块地砖的面积为( )
A.50 B.40 C.30 D.20
7.清代著名数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形 的方
法证明了勾股定理(如图).设四个全等直角三角形的较短直角边为 ,较长直角边为 ,五边形
7
的面积为 1,Δ 的面积为 ,若 = 1,
1
2 = 5,则 的值为( ) 2
A.5 B.6 C.7 D.8
二、填空题
8.自从“双减”政策实施以来,各中小学开展了丰富多彩的活动.某校拟举办一次书法作品展览,要
在每张长和宽分别为50 和80 的矩形相片周围镶上一圈等宽的彩纸.根据美学观点,彩纸面积
为相片面积的1时较美观.若所镶彩纸的宽为 ,根据题意,列方程
3
为 .
9.学校课外生物小组的试验园地是长 35 米、宽 20 米的矩形,为便于管理,现要在中间开辟一横两
纵三条等宽的小道(如图),要使种植面积为 600 平方米,求小道的宽.若设小道的宽为 米,则可
列方程为 .
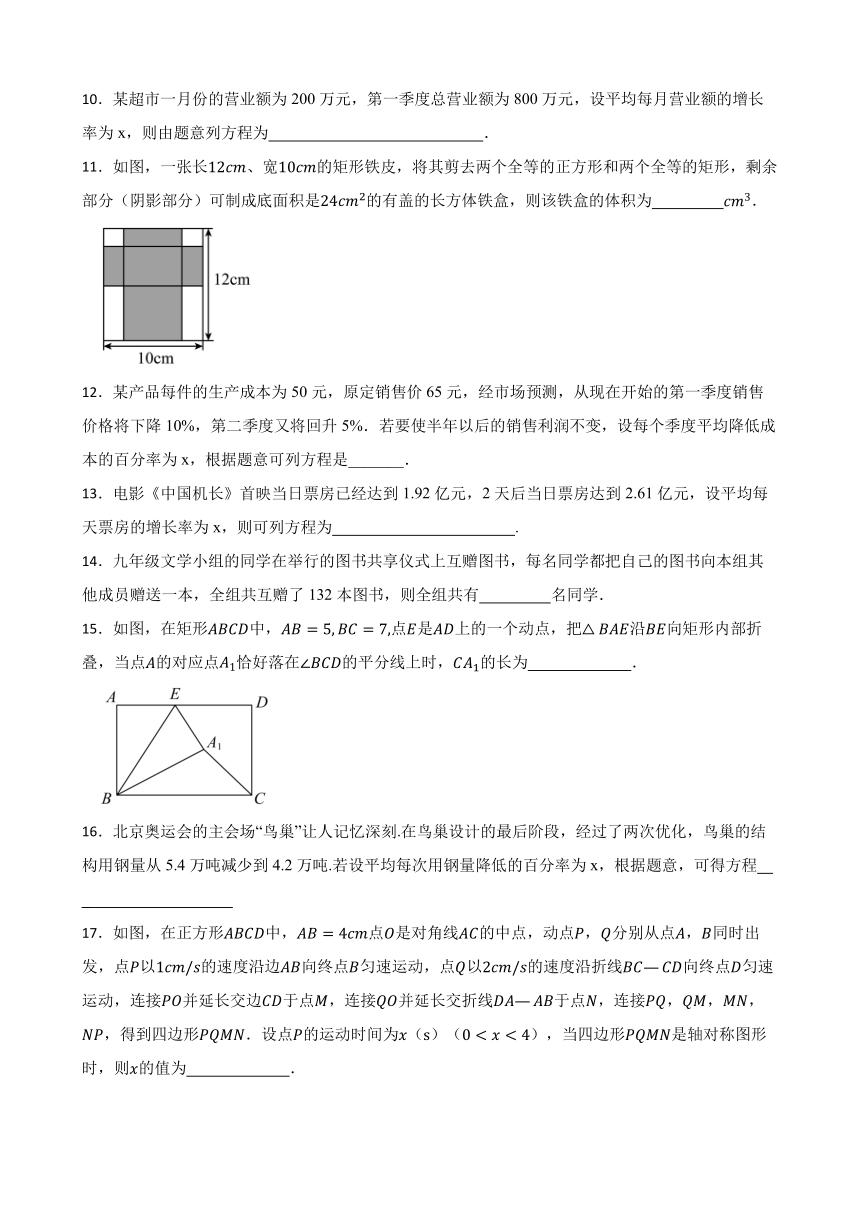
10.某超市一月份的营业额为 200 万元,第一季度总营业额为 800 万元,设平均每月营业额的增长
率为 x,则由题意列方程为 .
11.如图,一张长12 、宽10 的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余
部分(阴影部分)可制成底面积是24 2的有盖的长方体铁盒,则该铁盒的体积为 3.
12.某产品每件的生产成本为 50 元,原定销售价 65 元,经市场预测,从现在开始的第一季度销售
价格将下降 10%,第二季度又将回升 5%.若要使半年以后的销售利润不变,设每个季度平均降低成
本的百分率为 x,根据题意可列方程是_______.
13.电影《中国机长》首映当日票房已经达到 1.92 亿元,2 天后当日票房达到 2.61 亿元,设平均每
天票房的增长率为 x,则可列方程为 .
14.九年级文学小组的同学在举行的图书共享仪式上互赠图书,每名同学都把自己的图书向本组其
他成员赠送一本,全组共互赠了 132 本图书,则全组共有 名同学.
15.如图,在矩形 中, = 5, = 7,点 是 上的一个动点,把△ 沿 向矩形内部折
叠,当点 的对应点 1恰好落在∠ 的平分线上时, 1的长为 .
16.北京奥运会的主会场“鸟巢”让人记忆深刻.在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结
构用钢量从 5.4 万吨减少到 4.2 万吨.若设平均每次用钢量降低的百分率为 x,根据题意,可得方程
_
17.如图,在正方形 中, = 4 点 是对角线 的中点,动点 , 分别从点 , 同时出
发,点 以1 / 的速度沿边 向终点 匀速运动,点 以2 / 的速度沿折线 — 向终点 匀速
运动,连接 并延长交边 于点 ,连接 并延长交折线 — 于点 ,连接 , , ,
,得到四边形 .设点 的运动时间为 (s)(0 < < 4),当四边形 是轴对称图形
时,则 的值为 .
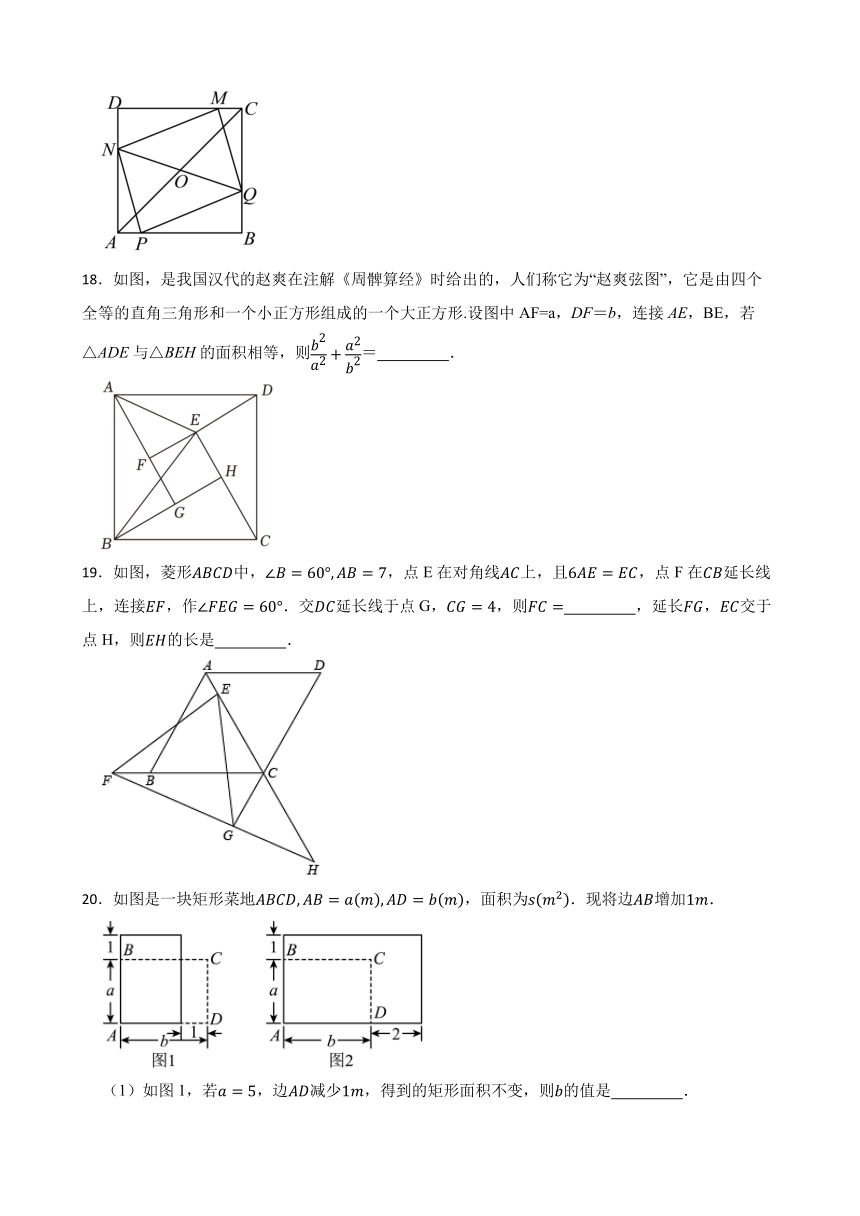
18.如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个
全等的直角三角形和一个小正方形组成的一个大正方形.设图中 AF=a,DF=b,连接 AE,BE,若
2 2
△ADE与△BEH的面积相等,则 + = .
2 2
19.如图,菱形 中,∠ = 60°, = 7,点 E 在对角线 上,且6 = ,点 F 在 延长线
上,连接 ,作∠ = 60°.交 延长线于点 G, = 4,则 = ,延长 , 交于
点 H,则 的长是 .
20.如图是一块矩形菜地 , = ( ), = ( ),面积为 ( 2).现将边 增加1 .
(1)如图 1,若 = 5,边 减少1 ,得到的矩形面积不变,则 的值是 .
(2)如图 2,若边 增加2 ,有且只有一个 的值,使得到的矩形面积为2 ( 2),则 的值
是 .
三、解答题
21.张师傅今年初开了一家商店,二月份开始盈利,二月份的盈利是 5000 元,四月份的盈利达到
7200 元,且从今年二月到四月,每月盈利的平均增长率都相同.求每月盈利的平均增长率.
22.如图,某单位准备将院内一块长30 ,宽20 的长方形花园中修两条纵向平行和一条横向弯折
的小道,剩余的地方种植花草,如图,要使种植花草的面积为532 2,求小道进出口的宽度.
23.从前有一天,一个笨汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽 4 尺,竖着比门框高 2
尺.他的邻居教他沿着门的两个对角斜着拿竿,这个笨汉一试,不多不少刚好进去了.请求出竹竿
的长度.
24.为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行收费标准如下:
春游活动结束后,该班共支付给该旅行社活动费用 2800 元,请问该班共有多少人参加这次春游活
动?
25.某童装专卖店在销售中发现,一款童装每件进价为 80 元,销售价为 120 元时,每天可售出 20
件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市
场调查发现,如果每件童装降价 1 元,那么平均可多售出 2 件.
(1)设每件童装降价 x元时,每天可销售 件,每件盈利 元;(用
x的代数式表示)
(2)每件童装降价多少元时,平均每天盈利 1200 元.
(3)要想平均每天盈利 2000 元,可能吗?请说明理由.
26.如图,利用一面墙(墙长 25m),用总长度为 70m 的栅栏(图中实线部分)围成一个矩形围栏
ABCD,且中间共留两个 1m 宽的小门.设栅栏 BC 的长为 xm.
(1)AB= m(用含 x 的代数式表示);
(2)若矩形围栏 ABCD 的面积为 324 2,求栅栏 BC 的长.
27.准备在一块长为 30 米,宽为 24 米的长方形花埔内修建四条宽度相等,且与各边垂直的小路,(
如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的 4 倍,若四条小路所占
面积为 80 平方米,则小路的宽度为多少米?
28. 2022 年受新型冠状病毒疫情的影响,水果电商有了意想不到的机遇,据统计某水果电商平台
1 月份的销售额是 225 万元,第一季度的销售额是 819 万元.
(1)若该平台 1 月份到 3 月份的月平均增长率都相同,求月平均增长率是多少?
(2)市场调查发现,某水果在电商平台上的售价为 24 元/千克时,每天能销售 300 千克,售价每
降低 2 元,每天可多售出 100 千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知
该水果的成本价为 12 元/千克,若使销售该水果每天获利 4000 元,则售价应降低多少元?
29.“品中华诗词,寻文化基因”,某校举办了第二届“中华诗词大赛”,将该校七年级参加竞赛的学生
成绩统计后,绘制了如下不完整的频数表与如图所示的频数直方图.
参加竞赛的学生成绩频数表
组别 成绩 x(分) 人数 百分比
A 60≤x<70 8 20%
B 70≤x<80 16 m%
C 80≤x<90 a 30%
D 90≤x≤100 4 10%
参加竞赛的学生成绩频数直方图
解决下列问题:
(1)表中 a= ,m= .
(2)补全频数直方图.
(3)方方参加了这次竞赛,成绩下来后,他对圆圆说:“我这次竞赛的成绩位于中游,比我答得
好的人比比我答得差的人少 3 个.”请你算一算,方方是第几名?
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】C
【解答】解:设参加此次比赛的球队数为 x 队,根据题意得:
1
x(x﹣1)=28,
2
化简,得 x2﹣x﹣56=0,
解得 x1=8,x2=﹣7(舍去),
答:参加此次比赛的球队数是 8 队.
故答案为:C.
【分析】根据球赛问题模型列出方程即可求解。
4.【答案】A
【解答】解:设平均每次用钢量降低的百分率为 x,根据题意得:
5.4(1﹣x)2=4.2,
故答案为:A.
【分析】根据题意可得等量关系:5.4 万吨×(1﹣降低的百分率)2=4.2,根据等量关系列出方程即
可.
5.【答案】D
【解答】由于每个人都和自己之外的其余 ( 1) 个人握了一次手,则 个人共握手 ( 1)
次,但由于甲与乙握手和乙与甲握手只能算作一次,故握手总次数为: ( 1) ,由此可列方程
2
为: ( 1)
= 45
.
故答案为:D.
【分析】由题意可知:每个人都会握(x-1)次手,所以 个人共握手 ( 1)次,而每两个人的一
次握手重复计算了一次,所以可得握手手总次数为: ( 1) ,于是可根据题意列方程。
2
6.【答案】B
7.【答案】A
8 1.【答案】(50 + 2 )(80 + 2 ) 50 × 80 = × 50 × 80(答案不唯一) 3
9.【答案】(35 2 )(20 ) = 600(或2 2 75 + 100 = 0)
10.【答案】200 + 200(1 + ) + 200(1 + )2 = 800
11.【答案】48
12.【答案】
13.【答案】1.92(1+x)2=2.61
【解答】解:设平均每天票房的增长率为 x,
根据题意得:1.92(1+x)2=2.61.
故答案为:1.92(1+x)2=2.61.
【分析】此题是一道平均增长率的问题, 根据公式 a(1+x)n=p,其中 a 是平均增长开始的量,x 是增
长率,n 是增长次数,P 是增长结束达到的量,根据公式即可列出方程即可
14.【答案】12
15.【答案】3√2或4√2
16.【答案】5.4(1-x)2=4.2
【解答】解:根据题意有:5.4(1-x)2=4.2.
故答案为:5.4(1-x)2=4.2.
【分析】此题是一道平均降低率的问题,根据公式 a(1-x)n=p,其中 a 是平均降低开始的量,x 是降低
率,n 是降低次数,P 是降低结束达到的量,根据公式即可列出方程.
17 4或8.【答案】
3 3
18.【答案】3
【解答】解:∵ = , = ,
∴ = = , = = = ,
∵ △ 与△ 的面积相等,
1 1
∴
2 = 2
,
1 1
∴b 2 ( )
2 = 2
,
∴ 2 = 2 ,
2
∴ 1 = ( ) ,
2
∴
2 1 = 0
,
解得
√5+1
= (负值舍去), 2
2
2
2
√5+1 2 2∴
2 + 2 = ( 2 ) + ( ) = 3
;
√5+1
故答案为:3.
【分析】本题考查了勾股定理的证明,一元二次方程的解法,三角形的面积,根据题意得出关于 的
2
方程是解题的关键.由△ 与△ 的面积相等得出: 2 = 2 ,即
2 1 = 0
,解方程
2
得到
√5+1 2(负值舍去)代入 + 中进行计算即可得到结论.
= 2 2 2
19 ;38.【答案】10
3
20.【答案】6;6 + 4√2
21.【答案】20%
22.【答案】小道进出口的宽度应为 1 米.
23.【答案】10 尺
24.【答案】该班参加这次春游活动的人数为 35 名.
25.【答案】(1)(20+2x);(40-x)
(2)解:根据题意,得:(20+2x)(40-x)=1200,
解得:x1=20,x2=10,
∵要扩大销售量,
∴x=20,
答:每件童装降价 20 元,平均每天盈利 1200 元;
(3)解:不能,理由如下:
(20+2x)(40-x)=2000,
整理,得:x2-30x+600=0,
∵Δ=(-30)2-4×600=-1500<0,
∴此方程无实数根,
故不可能做到平均每天盈利 2000 元.
【解答】解:(1)∵每件童装降价 1 元,那么平均可多售出 2 件,
∴每件童装降价 x元时,每天可销售:(20 + 2 ),
∵每件衣服可盈利:120 80 = 40,
∴当每件童装降价 x元时,每件衣服可盈利:40 ,
故答案为:(20+2x),(40-x).
【分析】(1)根据"每件童装降价 1 元,那么平均可多售出 2 件",即可计算出降价 x 元,可销售出
的衣服件数,即可求解;
(2)根据盈利=销售件数×利润,即可求解;
(3)根据盈利=销售件数×利润,列出方程,计算根的判别式即可求解.
26.【答案】(1)(72-3x)
(2)解:根据题意,得 x(72-3x)=324,
解得 x=18 或 x=6.
当 x=18 时,72-3x=72-3×18=18<25,符合题意;
当 x=6 时,72-3.x=72-3×6=54>25,不符合意,舍去。
答:栅栏 BC 的长为 18 m.
【解答】解: (1)AB=70+1×2-3x=(72-3x)米,
故答案为:(72-3x).
【分析】 (1)根据"AB 的长=栅栏的总长+两个 1m 宽的小门 -3 个 BC 的长"求解;
(2)根据“矩形围栏 ABCD 面积为 324 平方米”,列出关于 x 的一元二次方程求解,并对各个解的实
际意义验证后得出 BC 的长.
27.【答案】解:设小路的宽度为 x 米,则小正方形的边长为 4x 米,
依题意得:(30+4x+24+4x)x=80
整理得:4x2+27x-40=0,
解得 x1=-8(舍去),
5
x2= .
4
答:小路的宽度为5米.
4
【解析】【分析】设小路的宽度为 x 米,则小正方形的边长为 4x 米,根据小路的横向总长度(30+4x)
米和纵向总长度(24+4x)米,建立方程,解方程即可求出答案.
28.【答案】(1)解:设月平均增长率为 x,则:225+225(1+x)+225(1+x)2=819,
解得:x1=0.2,x2=-3.2(舍去),
∴月平均增长率是 20%.
(2)解: 设售价应降低 y 元,则: (24 12 )(300 + × 100) = 4000, 2
解得:y1=4,y2=2(舍去),
∴若使销售该水果每天获利 4000 元,则售价应降低 4 元.
【解析】【分析】(1)设月平均增长率为 x,根据题意列出关于 x 的一元二次方程,并解出符合题
意的 x 即可;
(2)设售价应降低 y 元,根据题意列出关于 y 的一元二次方程,并解出符合题意的 y 即可.
29.【答案】(1)12;40
(2)解:80≤x<90 频数为 12,故高度为 12,补全频数直方图如下:
(3)解:设比方方答得好的人为 x 人,则比方方答得差的人数为(x-3)人,
x+(x+3)+1=40,解得 x=18;
故方方是第 19 名;
【解答】解:(1)、由频数表可得 A 组的人数为 8,百分比为 20%,则总人数为8 ÷ 20% = 40
(人);
a=40-8-16-4=12(人);
m=100-20-30-10=40;
【分析】(1)、先根据 A 组的人数和百分比求出总人数,然后根据总人数减 ABD 组的人数,可得 C
组人数;根据四组百分比的和为 100%可得 m.
(2)、频数的高度为组别 C 的人数.
(3)、比方方答得好的加上比方方答得差的加上方方自己等于总人数可得.
一、单选题
1.庆“元旦”,市工会组织篮球比赛,赛制分为主场、客场交替进行,共进行了 72 场比赛,若设这
次有 x 队参加比赛,则根据题意可列方程为( )
1
A. x(x+1)=72 B.x(x+1)=72
2
1
C. x(x-1)=72 D.x(x-1)=72
2
2.某厂家 2024 年 1~5 月份销售的电车数量如图所示.设从 2 月份到 4 月份,该厂家电车销售的平
均月增长率为 ,根据题意可得方程( )
A.140(1 )2 = 461 B.180(1 + )2 = 461
C.450(1 )2 = 368 D.368(1 + )2 = 450
3.某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛 28 场,则参加此次比赛
的球队数是( )
A.6 B.7 C.8 D.9
4.北京奥运会的主会场“鸟巢”让人记忆深刻.在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结构
用钢量从 5.4 万吨减少到 4.2 万吨.若设平均每次用钢量降低的百分率为 x,根据题意,可得方程
( )
A.5.4(1﹣x)2=4.2 B.5.4(1﹣x2)=4.2
C.5.4(1﹣2x)=4.2 D.4.2(1+x)2=5.4
5.在某次同学聚会上,每两个人都握一次手,所有人共握手 45 次,设有 x 人参加这次聚会,则列
出方程正确的是( )
A.x(x+1)=45 B.x(x﹣1)=45
C. =45 D. =45
6.如图,一块正方形地砖的图案是由 4 个全等的五边形和 1 个小正方形组成的,已知小正方形的面
积和五边形的面积相等,并且图中线段 a 的长度为√10 2,则这块地砖的面积为( )
A.50 B.40 C.30 D.20
7.清代著名数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形 的方
法证明了勾股定理(如图).设四个全等直角三角形的较短直角边为 ,较长直角边为 ,五边形
7
的面积为 1,Δ 的面积为 ,若 = 1,
1
2 = 5,则 的值为( ) 2
A.5 B.6 C.7 D.8
二、填空题
8.自从“双减”政策实施以来,各中小学开展了丰富多彩的活动.某校拟举办一次书法作品展览,要
在每张长和宽分别为50 和80 的矩形相片周围镶上一圈等宽的彩纸.根据美学观点,彩纸面积
为相片面积的1时较美观.若所镶彩纸的宽为 ,根据题意,列方程
3
为 .
9.学校课外生物小组的试验园地是长 35 米、宽 20 米的矩形,为便于管理,现要在中间开辟一横两
纵三条等宽的小道(如图),要使种植面积为 600 平方米,求小道的宽.若设小道的宽为 米,则可
列方程为 .
10.某超市一月份的营业额为 200 万元,第一季度总营业额为 800 万元,设平均每月营业额的增长
率为 x,则由题意列方程为 .
11.如图,一张长12 、宽10 的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余
部分(阴影部分)可制成底面积是24 2的有盖的长方体铁盒,则该铁盒的体积为 3.
12.某产品每件的生产成本为 50 元,原定销售价 65 元,经市场预测,从现在开始的第一季度销售
价格将下降 10%,第二季度又将回升 5%.若要使半年以后的销售利润不变,设每个季度平均降低成
本的百分率为 x,根据题意可列方程是_______.
13.电影《中国机长》首映当日票房已经达到 1.92 亿元,2 天后当日票房达到 2.61 亿元,设平均每
天票房的增长率为 x,则可列方程为 .
14.九年级文学小组的同学在举行的图书共享仪式上互赠图书,每名同学都把自己的图书向本组其
他成员赠送一本,全组共互赠了 132 本图书,则全组共有 名同学.
15.如图,在矩形 中, = 5, = 7,点 是 上的一个动点,把△ 沿 向矩形内部折
叠,当点 的对应点 1恰好落在∠ 的平分线上时, 1的长为 .
16.北京奥运会的主会场“鸟巢”让人记忆深刻.在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结
构用钢量从 5.4 万吨减少到 4.2 万吨.若设平均每次用钢量降低的百分率为 x,根据题意,可得方程
_
17.如图,在正方形 中, = 4 点 是对角线 的中点,动点 , 分别从点 , 同时出
发,点 以1 / 的速度沿边 向终点 匀速运动,点 以2 / 的速度沿折线 — 向终点 匀速
运动,连接 并延长交边 于点 ,连接 并延长交折线 — 于点 ,连接 , , ,
,得到四边形 .设点 的运动时间为 (s)(0 < < 4),当四边形 是轴对称图形
时,则 的值为 .
18.如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个
全等的直角三角形和一个小正方形组成的一个大正方形.设图中 AF=a,DF=b,连接 AE,BE,若
2 2
△ADE与△BEH的面积相等,则 + = .
2 2
19.如图,菱形 中,∠ = 60°, = 7,点 E 在对角线 上,且6 = ,点 F 在 延长线
上,连接 ,作∠ = 60°.交 延长线于点 G, = 4,则 = ,延长 , 交于
点 H,则 的长是 .
20.如图是一块矩形菜地 , = ( ), = ( ),面积为 ( 2).现将边 增加1 .
(1)如图 1,若 = 5,边 减少1 ,得到的矩形面积不变,则 的值是 .
(2)如图 2,若边 增加2 ,有且只有一个 的值,使得到的矩形面积为2 ( 2),则 的值
是 .
三、解答题
21.张师傅今年初开了一家商店,二月份开始盈利,二月份的盈利是 5000 元,四月份的盈利达到
7200 元,且从今年二月到四月,每月盈利的平均增长率都相同.求每月盈利的平均增长率.
22.如图,某单位准备将院内一块长30 ,宽20 的长方形花园中修两条纵向平行和一条横向弯折
的小道,剩余的地方种植花草,如图,要使种植花草的面积为532 2,求小道进出口的宽度.
23.从前有一天,一个笨汉拿着竹竿进屋,横拿竖拿都进不去,横着比门框宽 4 尺,竖着比门框高 2
尺.他的邻居教他沿着门的两个对角斜着拿竿,这个笨汉一试,不多不少刚好进去了.请求出竹竿
的长度.
24.为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行收费标准如下:
春游活动结束后,该班共支付给该旅行社活动费用 2800 元,请问该班共有多少人参加这次春游活
动?
25.某童装专卖店在销售中发现,一款童装每件进价为 80 元,销售价为 120 元时,每天可售出 20
件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市
场调查发现,如果每件童装降价 1 元,那么平均可多售出 2 件.
(1)设每件童装降价 x元时,每天可销售 件,每件盈利 元;(用
x的代数式表示)
(2)每件童装降价多少元时,平均每天盈利 1200 元.
(3)要想平均每天盈利 2000 元,可能吗?请说明理由.
26.如图,利用一面墙(墙长 25m),用总长度为 70m 的栅栏(图中实线部分)围成一个矩形围栏
ABCD,且中间共留两个 1m 宽的小门.设栅栏 BC 的长为 xm.
(1)AB= m(用含 x 的代数式表示);
(2)若矩形围栏 ABCD 的面积为 324 2,求栅栏 BC 的长.
27.准备在一块长为 30 米,宽为 24 米的长方形花埔内修建四条宽度相等,且与各边垂直的小路,(
如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的 4 倍,若四条小路所占
面积为 80 平方米,则小路的宽度为多少米?
28. 2022 年受新型冠状病毒疫情的影响,水果电商有了意想不到的机遇,据统计某水果电商平台
1 月份的销售额是 225 万元,第一季度的销售额是 819 万元.
(1)若该平台 1 月份到 3 月份的月平均增长率都相同,求月平均增长率是多少?
(2)市场调查发现,某水果在电商平台上的售价为 24 元/千克时,每天能销售 300 千克,售价每
降低 2 元,每天可多售出 100 千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知
该水果的成本价为 12 元/千克,若使销售该水果每天获利 4000 元,则售价应降低多少元?
29.“品中华诗词,寻文化基因”,某校举办了第二届“中华诗词大赛”,将该校七年级参加竞赛的学生
成绩统计后,绘制了如下不完整的频数表与如图所示的频数直方图.
参加竞赛的学生成绩频数表
组别 成绩 x(分) 人数 百分比
A 60≤x<70 8 20%
B 70≤x<80 16 m%
C 80≤x<90 a 30%
D 90≤x≤100 4 10%
参加竞赛的学生成绩频数直方图
解决下列问题:
(1)表中 a= ,m= .
(2)补全频数直方图.
(3)方方参加了这次竞赛,成绩下来后,他对圆圆说:“我这次竞赛的成绩位于中游,比我答得
好的人比比我答得差的人少 3 个.”请你算一算,方方是第几名?
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】C
【解答】解:设参加此次比赛的球队数为 x 队,根据题意得:
1
x(x﹣1)=28,
2
化简,得 x2﹣x﹣56=0,
解得 x1=8,x2=﹣7(舍去),
答:参加此次比赛的球队数是 8 队.
故答案为:C.
【分析】根据球赛问题模型列出方程即可求解。
4.【答案】A
【解答】解:设平均每次用钢量降低的百分率为 x,根据题意得:
5.4(1﹣x)2=4.2,
故答案为:A.
【分析】根据题意可得等量关系:5.4 万吨×(1﹣降低的百分率)2=4.2,根据等量关系列出方程即
可.
5.【答案】D
【解答】由于每个人都和自己之外的其余 ( 1) 个人握了一次手,则 个人共握手 ( 1)
次,但由于甲与乙握手和乙与甲握手只能算作一次,故握手总次数为: ( 1) ,由此可列方程
2
为: ( 1)
= 45
.
故答案为:D.
【分析】由题意可知:每个人都会握(x-1)次手,所以 个人共握手 ( 1)次,而每两个人的一
次握手重复计算了一次,所以可得握手手总次数为: ( 1) ,于是可根据题意列方程。
2
6.【答案】B
7.【答案】A
8 1.【答案】(50 + 2 )(80 + 2 ) 50 × 80 = × 50 × 80(答案不唯一) 3
9.【答案】(35 2 )(20 ) = 600(或2 2 75 + 100 = 0)
10.【答案】200 + 200(1 + ) + 200(1 + )2 = 800
11.【答案】48
12.【答案】
13.【答案】1.92(1+x)2=2.61
【解答】解:设平均每天票房的增长率为 x,
根据题意得:1.92(1+x)2=2.61.
故答案为:1.92(1+x)2=2.61.
【分析】此题是一道平均增长率的问题, 根据公式 a(1+x)n=p,其中 a 是平均增长开始的量,x 是增
长率,n 是增长次数,P 是增长结束达到的量,根据公式即可列出方程即可
14.【答案】12
15.【答案】3√2或4√2
16.【答案】5.4(1-x)2=4.2
【解答】解:根据题意有:5.4(1-x)2=4.2.
故答案为:5.4(1-x)2=4.2.
【分析】此题是一道平均降低率的问题,根据公式 a(1-x)n=p,其中 a 是平均降低开始的量,x 是降低
率,n 是降低次数,P 是降低结束达到的量,根据公式即可列出方程.
17 4或8.【答案】
3 3
18.【答案】3
【解答】解:∵ = , = ,
∴ = = , = = = ,
∵ △ 与△ 的面积相等,
1 1
∴
2 = 2
,
1 1
∴b 2 ( )
2 = 2
,
∴ 2 = 2 ,
2
∴ 1 = ( ) ,
2
∴
2 1 = 0
,
解得
√5+1
= (负值舍去), 2
2
2
2
√5+1 2 2∴
2 + 2 = ( 2 ) + ( ) = 3
;
√5+1
故答案为:3.
【分析】本题考查了勾股定理的证明,一元二次方程的解法,三角形的面积,根据题意得出关于 的
2
方程是解题的关键.由△ 与△ 的面积相等得出: 2 = 2 ,即
2 1 = 0
,解方程
2
得到
√5+1 2(负值舍去)代入 + 中进行计算即可得到结论.
= 2 2 2
19 ;38.【答案】10
3
20.【答案】6;6 + 4√2
21.【答案】20%
22.【答案】小道进出口的宽度应为 1 米.
23.【答案】10 尺
24.【答案】该班参加这次春游活动的人数为 35 名.
25.【答案】(1)(20+2x);(40-x)
(2)解:根据题意,得:(20+2x)(40-x)=1200,
解得:x1=20,x2=10,
∵要扩大销售量,
∴x=20,
答:每件童装降价 20 元,平均每天盈利 1200 元;
(3)解:不能,理由如下:
(20+2x)(40-x)=2000,
整理,得:x2-30x+600=0,
∵Δ=(-30)2-4×600=-1500<0,
∴此方程无实数根,
故不可能做到平均每天盈利 2000 元.
【解答】解:(1)∵每件童装降价 1 元,那么平均可多售出 2 件,
∴每件童装降价 x元时,每天可销售:(20 + 2 ),
∵每件衣服可盈利:120 80 = 40,
∴当每件童装降价 x元时,每件衣服可盈利:40 ,
故答案为:(20+2x),(40-x).
【分析】(1)根据"每件童装降价 1 元,那么平均可多售出 2 件",即可计算出降价 x 元,可销售出
的衣服件数,即可求解;
(2)根据盈利=销售件数×利润,即可求解;
(3)根据盈利=销售件数×利润,列出方程,计算根的判别式即可求解.
26.【答案】(1)(72-3x)
(2)解:根据题意,得 x(72-3x)=324,
解得 x=18 或 x=6.
当 x=18 时,72-3x=72-3×18=18<25,符合题意;
当 x=6 时,72-3.x=72-3×6=54>25,不符合意,舍去。
答:栅栏 BC 的长为 18 m.
【解答】解: (1)AB=70+1×2-3x=(72-3x)米,
故答案为:(72-3x).
【分析】 (1)根据"AB 的长=栅栏的总长+两个 1m 宽的小门 -3 个 BC 的长"求解;
(2)根据“矩形围栏 ABCD 面积为 324 平方米”,列出关于 x 的一元二次方程求解,并对各个解的实
际意义验证后得出 BC 的长.
27.【答案】解:设小路的宽度为 x 米,则小正方形的边长为 4x 米,
依题意得:(30+4x+24+4x)x=80
整理得:4x2+27x-40=0,
解得 x1=-8(舍去),
5
x2= .
4
答:小路的宽度为5米.
4
【解析】【分析】设小路的宽度为 x 米,则小正方形的边长为 4x 米,根据小路的横向总长度(30+4x)
米和纵向总长度(24+4x)米,建立方程,解方程即可求出答案.
28.【答案】(1)解:设月平均增长率为 x,则:225+225(1+x)+225(1+x)2=819,
解得:x1=0.2,x2=-3.2(舍去),
∴月平均增长率是 20%.
(2)解: 设售价应降低 y 元,则: (24 12 )(300 + × 100) = 4000, 2
解得:y1=4,y2=2(舍去),
∴若使销售该水果每天获利 4000 元,则售价应降低 4 元.
【解析】【分析】(1)设月平均增长率为 x,根据题意列出关于 x 的一元二次方程,并解出符合题
意的 x 即可;
(2)设售价应降低 y 元,根据题意列出关于 y 的一元二次方程,并解出符合题意的 y 即可.
29.【答案】(1)12;40
(2)解:80≤x<90 频数为 12,故高度为 12,补全频数直方图如下:
(3)解:设比方方答得好的人为 x 人,则比方方答得差的人数为(x-3)人,
x+(x+3)+1=40,解得 x=18;
故方方是第 19 名;
【解答】解:(1)、由频数表可得 A 组的人数为 8,百分比为 20%,则总人数为8 ÷ 20% = 40
(人);
a=40-8-16-4=12(人);
m=100-20-30-10=40;
【分析】(1)、先根据 A 组的人数和百分比求出总人数,然后根据总人数减 ABD 组的人数,可得 C
组人数;根据四组百分比的和为 100%可得 m.
(2)、频数的高度为组别 C 的人数.
(3)、比方方答得好的加上比方方答得差的加上方方自己等于总人数可得.
同课章节目录
