2026年中考《数学》复习课件 专题六 圆--微专题(十三) 求与圆有关的不规则图形面积的方法(共28张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件 专题六 圆--微专题(十三) 求与圆有关的不规则图形面积的方法(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 09:50:02 | ||
图片预览





文档简介
(共28张PPT)
复习讲义
第一篇 考点精讲
专题六 圆
微专题(十三) 求与圆有关的不规则图形面积的方
法
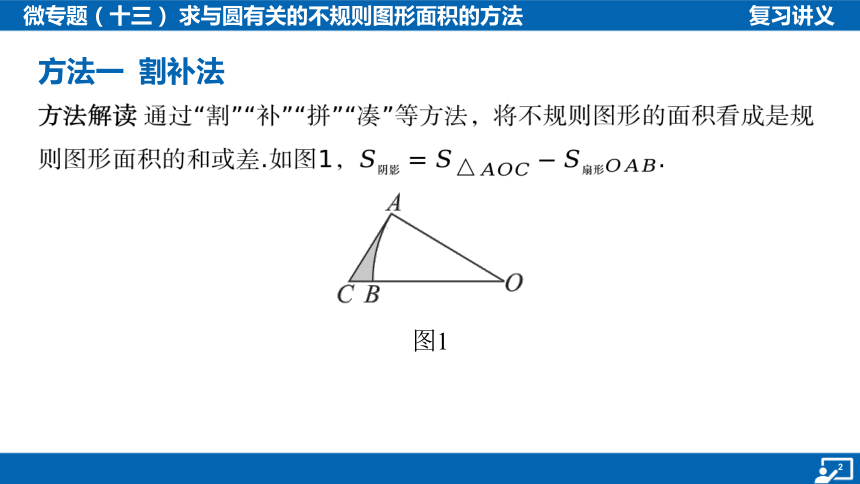
方法一 割补法
方法解读 通过“割”“补”“拼”“凑”等方法,将不规则图形的面积看成是规
则图形面积的和或差.如图1, .
图1
方法应用
图2
1.(2025·四川遂宁·中考模拟)工人师傅在检查排污管道时发现
淤泥堆积.如图2,排污管道的横截面是直径为 的圆,为
预估淤泥量,测得淤泥横截面(图中阴影部分)宽 为
,经计算得出淤泥横截面的面积是( ).
A. B.
C. D.
图50
提示:如图50,过点作 于点D,则
.因为圆的直径为 ,所以
.在 中,
.因为 ,所以
【答案】A
为等边三角形.所以 .故淤泥横截面的面
积 .
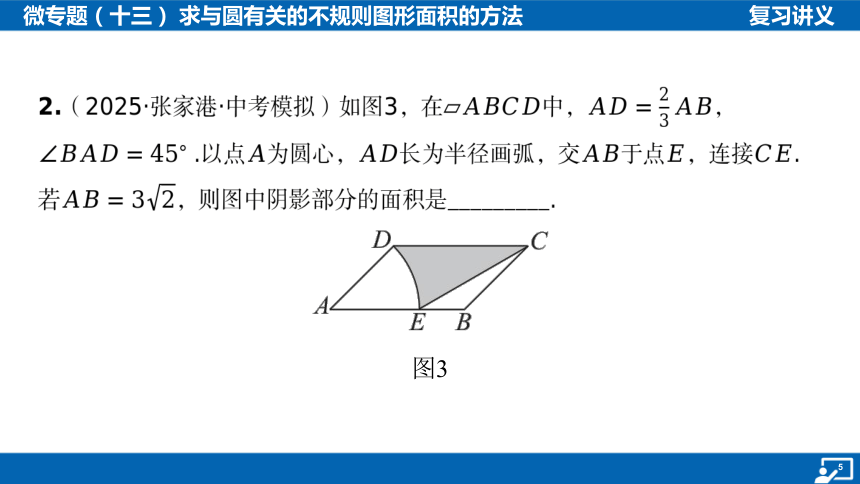
2.(2025·张家港·中考模拟)如图3,在中, ,
.以点为圆心,长为半径画弧,交于点,连接 .
若 ,则图中阴影部分的面积是_________.
图3
.由题意可
知,,所以 .故
.
图51
提示:过点作于点 .因为
, ,所以
.在 中,
【答案】
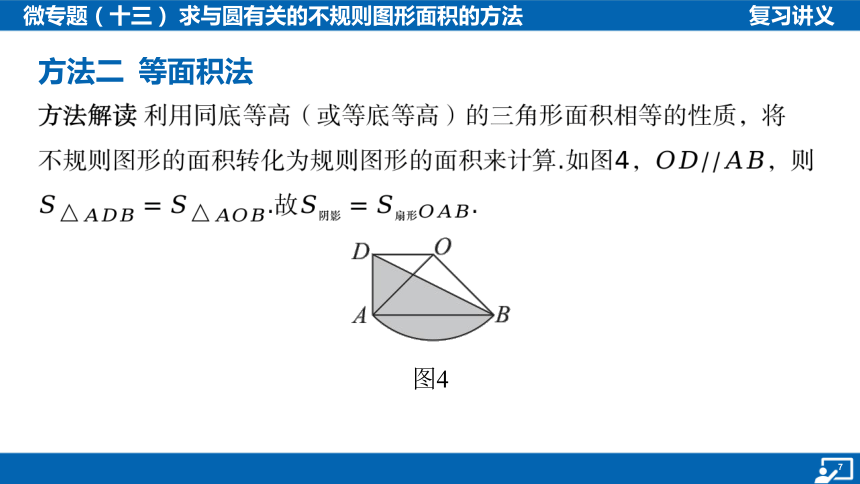
方法二 等面积法
方法解读 利用同底等高(或等底等高)的三角形面积相等的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图4, ,则
.故 .
图4
方法应用
图5
3.(2023·四川广元·中考)如图5,在半径为5的扇形
中, ,是上一点, ,
,垂足分别为点,.若 ,则图中阴
影部分的面积为( ).
B
A. B. C. D.
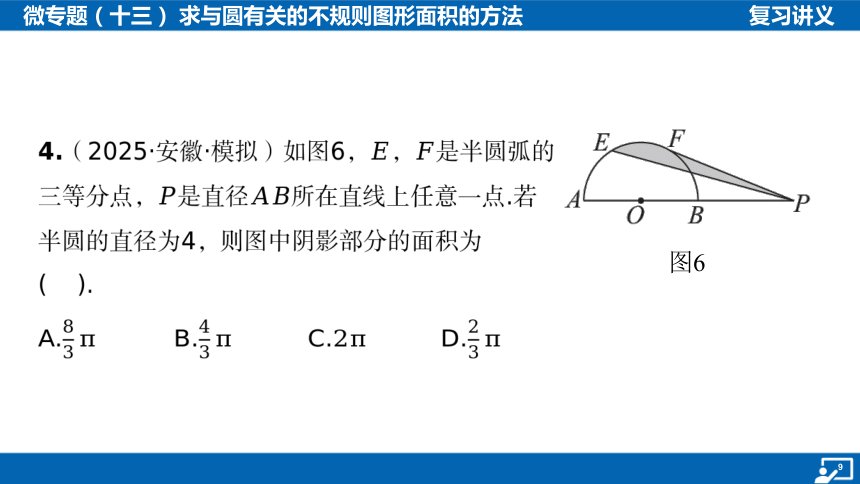
图6
4.(2025·安徽·模拟)如图6,, 是半圆弧的
三等分点,是直径 所在直线上任意一点.若
半圆的直径为4,则图中阴影部分的面积为
( ).
A. B. C. D.
图6
提示:如图51,连接,,.因为, 是
半圆弧的三等分点,所以 .所以
.因
【答案】D
为,所以是等边三角形.所以 .由此
可得,.所以.故 .
方法三 图形变换法
方法解读 利用图形在平移、旋转、对称变换前后面积不变的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图7,绕点
旋转得到,则 .
图7
方法应用
图8
5.如图8,网格图中每个小正方形的边长均为1,以
为半径的扇形经过平移到达扇形 的位
置,那么图中阴影部分的面积是( ).
B
A.8 B.6 C.6.5 D.7.5
图9
6.如图9,直径长为6的半圆绕点 顺时针旋转
,此时点旋转到点 处,则图中阴影部分的
面积是( ).
D
A. B. C. D.
方法四 整体法
方法解读 当阴影部分图形由较多规则图形组成时,可以将阴影部分图
形视为一个整体来计算其面积.如图10,与 的半径相同,两个小
扇形的圆心角未知,则阴影部分的面积可以转化为圆心角为 的扇形
面积来计算.
图10
方法应用
图11
7.(2025·青海西宁·中考改编)如图11,等边三角形 内接
于, ,则图中阴影部分的面积是_ __.
提示:因为为等边三角形,且内接于 ,所以
, .过点作 于点
【答案】
.在中,, , ,
所以 , .所以
.所以 .
图11
图12
8.(2023·重庆·中考)如图12,在矩形 中,
,,为的中点,连接,.以点 为圆
心,长为半径画弧,分别与,交于点, ,则图
中阴影部分的面积为______.
提示:因为,为的中点,所以 .
又,所以 .所以
.所以
.
微专题练习(十三) 求与圆有关的不规则图形面积的方法
方法一 割补法
图1
1.(2025·湖北鄂州·中考模拟)如图1,在 中,
, ,,点为 的
中点.以为圆心,长为半径作半圆,交于点 ,
则图中阴影部分的面积是( ).
A. B. C. D.
提示:连接, .
C
图2
2.(2025·广西梧州·中考模拟)如图2,四边形是 的
内接正四边形,分别以点,为圆心,以大于 的长
为半径画弧,两弧相交于点,,作直线,交
于点,.若,则,, 所围成的阴影部分
的面积为_ __________.
图73
提示:如图73,连接,.由题意可知,直线 垂
直平分线段,所以.又因为 ,所以
为等边三角形.所以 .因为四边形
是的内接正四边形,所以 .所以
.所以 .
【答案】
方法二 等面积法
3.(2023·内蒙古·中考)如图3,正方形的边长为2,对角线 ,
相交于点.以点为圆心,对角线的长为半径画弧,交 的延长
线于点 ,则图中阴影部分的面积为___.
图3
4.(2025·山西·模拟)半圆的直径 在直尺上所对的刻度如图4所示,点
在半圆上,且,连接,取的中点,连接 ,则图中
阴影部分的面积为( ).
图4
A. B. C. D.
图74
提示:如图74,取的中点 ,连接
,, .由题意,得
, .因
为点D为的中点,所以 .从
【答案】A
而得,即.因为 ,所以
.又 ,所以 .故
.
方法三 图形变换法
图5
5.(2025·山东·模拟)如图5,在 中,已知
,将绕点逆时针旋转 得到
,点经过的路径为 ,则图中阴影部分的
面积为( ).
B
A. B. C. D.
提示: .
6.(2025·河南·中考模拟)如图6,将扇形沿方向平移,使点 移到
的中点处,得到扇形.若 , ,则阴影部分
的面积为_ ______.
图6
图75
提示:如图75,设交于点,连接 .因为
, ,又因为
,所以 .所以
, .所以
【答案】
, .由平移变换知,
.
方法四 整体法
图7
7.教材变式[人教版九上第123页第7题变式]某花园内有一
块五边形的空地如图7所示,为了美化环境,现计划在以五
边形各顶点为圆心, 长为半径的扇形区域(阴影部分)
种上花草,那么种上花草的扇形区域总面积是( ).
C
A. B. C. D.
提示:该五边形的内角和为 ,故扇形区域总面积
是 .
图8
8.如图8,在菱形中,对角线 ,
.分别以点,,,为圆心, 长为半
径画弧,与该菱形的边相交,则图中阴影部分的面
积为__________.
提示:在菱形中,, ,所以
.因为
,所以四个扇形的面积和等于
一个以 长为半径的圆的面积.故
.
复习讲义
第一篇 考点精讲
专题六 圆
微专题(十三) 求与圆有关的不规则图形面积的方
法
方法一 割补法
方法解读 通过“割”“补”“拼”“凑”等方法,将不规则图形的面积看成是规
则图形面积的和或差.如图1, .
图1
方法应用
图2
1.(2025·四川遂宁·中考模拟)工人师傅在检查排污管道时发现
淤泥堆积.如图2,排污管道的横截面是直径为 的圆,为
预估淤泥量,测得淤泥横截面(图中阴影部分)宽 为
,经计算得出淤泥横截面的面积是( ).
A. B.
C. D.
图50
提示:如图50,过点作 于点D,则
.因为圆的直径为 ,所以
.在 中,
.因为 ,所以
【答案】A
为等边三角形.所以 .故淤泥横截面的面
积 .
2.(2025·张家港·中考模拟)如图3,在中, ,
.以点为圆心,长为半径画弧,交于点,连接 .
若 ,则图中阴影部分的面积是_________.
图3
.由题意可
知,,所以 .故
.
图51
提示:过点作于点 .因为
, ,所以
.在 中,
【答案】
方法二 等面积法
方法解读 利用同底等高(或等底等高)的三角形面积相等的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图4, ,则
.故 .
图4
方法应用
图5
3.(2023·四川广元·中考)如图5,在半径为5的扇形
中, ,是上一点, ,
,垂足分别为点,.若 ,则图中阴
影部分的面积为( ).
B
A. B. C. D.
图6
4.(2025·安徽·模拟)如图6,, 是半圆弧的
三等分点,是直径 所在直线上任意一点.若
半圆的直径为4,则图中阴影部分的面积为
( ).
A. B. C. D.
图6
提示:如图51,连接,,.因为, 是
半圆弧的三等分点,所以 .所以
.因
【答案】D
为,所以是等边三角形.所以 .由此
可得,.所以.故 .
方法三 图形变换法
方法解读 利用图形在平移、旋转、对称变换前后面积不变的性质,将
不规则图形的面积转化为规则图形的面积来计算.如图7,绕点
旋转得到,则 .
图7
方法应用
图8
5.如图8,网格图中每个小正方形的边长均为1,以
为半径的扇形经过平移到达扇形 的位
置,那么图中阴影部分的面积是( ).
B
A.8 B.6 C.6.5 D.7.5
图9
6.如图9,直径长为6的半圆绕点 顺时针旋转
,此时点旋转到点 处,则图中阴影部分的
面积是( ).
D
A. B. C. D.
方法四 整体法
方法解读 当阴影部分图形由较多规则图形组成时,可以将阴影部分图
形视为一个整体来计算其面积.如图10,与 的半径相同,两个小
扇形的圆心角未知,则阴影部分的面积可以转化为圆心角为 的扇形
面积来计算.
图10
方法应用
图11
7.(2025·青海西宁·中考改编)如图11,等边三角形 内接
于, ,则图中阴影部分的面积是_ __.
提示:因为为等边三角形,且内接于 ,所以
, .过点作 于点
【答案】
.在中,, , ,
所以 , .所以
.所以 .
图11
图12
8.(2023·重庆·中考)如图12,在矩形 中,
,,为的中点,连接,.以点 为圆
心,长为半径画弧,分别与,交于点, ,则图
中阴影部分的面积为______.
提示:因为,为的中点,所以 .
又,所以 .所以
.所以
.
微专题练习(十三) 求与圆有关的不规则图形面积的方法
方法一 割补法
图1
1.(2025·湖北鄂州·中考模拟)如图1,在 中,
, ,,点为 的
中点.以为圆心,长为半径作半圆,交于点 ,
则图中阴影部分的面积是( ).
A. B. C. D.
提示:连接, .
C
图2
2.(2025·广西梧州·中考模拟)如图2,四边形是 的
内接正四边形,分别以点,为圆心,以大于 的长
为半径画弧,两弧相交于点,,作直线,交
于点,.若,则,, 所围成的阴影部分
的面积为_ __________.
图73
提示:如图73,连接,.由题意可知,直线 垂
直平分线段,所以.又因为 ,所以
为等边三角形.所以 .因为四边形
是的内接正四边形,所以 .所以
.所以 .
【答案】
方法二 等面积法
3.(2023·内蒙古·中考)如图3,正方形的边长为2,对角线 ,
相交于点.以点为圆心,对角线的长为半径画弧,交 的延长
线于点 ,则图中阴影部分的面积为___.
图3
4.(2025·山西·模拟)半圆的直径 在直尺上所对的刻度如图4所示,点
在半圆上,且,连接,取的中点,连接 ,则图中
阴影部分的面积为( ).
图4
A. B. C. D.
图74
提示:如图74,取的中点 ,连接
,, .由题意,得
, .因
为点D为的中点,所以 .从
【答案】A
而得,即.因为 ,所以
.又 ,所以 .故
.
方法三 图形变换法
图5
5.(2025·山东·模拟)如图5,在 中,已知
,将绕点逆时针旋转 得到
,点经过的路径为 ,则图中阴影部分的
面积为( ).
B
A. B. C. D.
提示: .
6.(2025·河南·中考模拟)如图6,将扇形沿方向平移,使点 移到
的中点处,得到扇形.若 , ,则阴影部分
的面积为_ ______.
图6
图75
提示:如图75,设交于点,连接 .因为
, ,又因为
,所以 .所以
, .所以
【答案】
, .由平移变换知,
.
方法四 整体法
图7
7.教材变式[人教版九上第123页第7题变式]某花园内有一
块五边形的空地如图7所示,为了美化环境,现计划在以五
边形各顶点为圆心, 长为半径的扇形区域(阴影部分)
种上花草,那么种上花草的扇形区域总面积是( ).
C
A. B. C. D.
提示:该五边形的内角和为 ,故扇形区域总面积
是 .
图8
8.如图8,在菱形中,对角线 ,
.分别以点,,,为圆心, 长为半
径画弧,与该菱形的边相交,则图中阴影部分的面
积为__________.
提示:在菱形中,, ,所以
.因为
,所以四个扇形的面积和等于
一个以 长为半径的圆的面积.故
.
同课章节目录
