2026年中考《数学》复习课件 专题三 函数--第14讲 二次函数的图象和性质(共67张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件 专题三 函数--第14讲 二次函数的图象和性质(共67张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 09:49:25 | ||
图片预览











文档简介
(共67张PPT)
复习讲义
第一篇 考点精讲
专题三 函数
第14讲 二次函数的图象和性质
聚焦核心
1.二次函数的定义
一般地,形如
叫作二次函数.其中
数、一次项系数和常数项.特别地,当
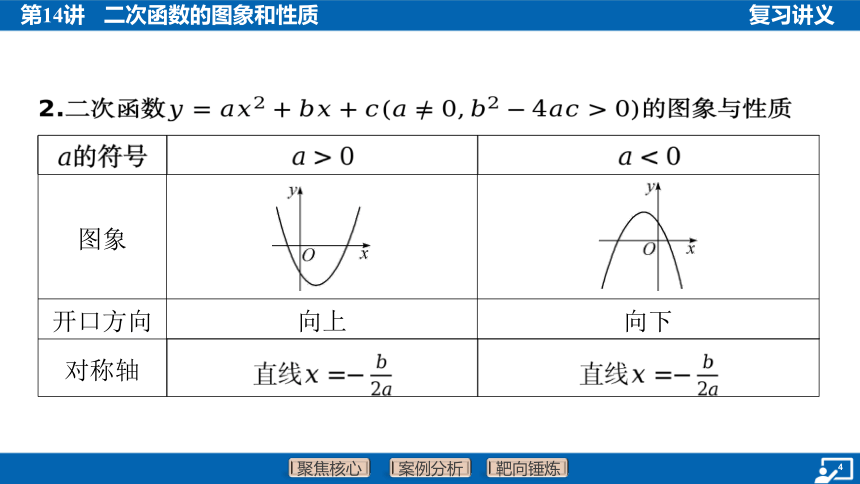
2.二次函数 的图象与性质
图象 ___________________________ ___________________________
开口方向 向上 向下
对称轴
顶点 坐标
增减性
减小
增大
增大
续表
减小
最值
大
续表
小
3.二次函数 的图象与其系数的关系
系数 图象特点
开口向____
开口向____
开口越____
开口越____
对称轴是___轴
上
下
小
大
左
右
系数 图象特点
经过____点
正
原
负
两
一
没有
续表
4.二次函数解析式的三种形式
(1)一般式:,,是常数,且 ,函数图象
与 轴的交点坐标是______.
(2)顶点式:,,是常数,且 ,函数图
象的顶点坐标是______.
(3)交点式:,,是常数,且 ,函
数图象与 轴的两个交点的坐标是_______,_______.
说明:通过配方可以把一般式 化为顶点式
,其中_____, .
第14讲 二次函数的图象和性质
案例分析
考点一 二次函数的图象和性质
名师指导
二次函数的很多性质(对称轴、顶点坐标、最值、增减性等)都可
以从函数解析式的顶点式中反映出来,所以研究二次函数的性质时,通
常将解析式化为顶点式,即
例1 关于二次函数 ,下列说法正确的是( ).
A.该函数图象与轴交于点
B.该函数图象的对称轴为直线
C.该函数图象的顶点坐标为
D.该函数的最大值是3
提示:在中,当时, ,所以该函数图象与
轴交于点 ,故说法A错误.因为
,所以该函数图象的对称轴为直线
,顶点坐标为,故说法B,C错误.因为 ,所以函数
图象开口向下.所以当 时,函数有最大值,最大值为3.故说法D正确.
D
思路点拨 将代入函数解析式,就可以求出函数图象与 轴的交点
坐标.将二次函数的一般式化为顶点式,就可以判断函数图象的对称轴、
顶点坐标和最值.
考点专练
1.(2023·四川甘孜·中考)下列关于二次函数 的说法正
确的是( ).
D
A.图象是一条开口向下的抛物线 B.图象与 轴没有交点
C.当时,随的增大而增大 D.图象的顶点坐标是
2.(2024·广东·中考)若点,,都在二次函数
的图象上,则( ).
A
A. B. C. D.
3.(2025·四川乐山·中考改编)已知二次函数 ,
当时,函数取得最大值;当时,函数取得最小值. 的取值
范围是( ).
A. B. C. D.
提示:因为当时,函数取得最小值,所以在 的范围
内,可取到1,所以.因为二次函数 的对称轴为直线
,所以时的函数值与 时的函数值相等,又因为当
时,函数取得最大值,所以,综上所述, 的取值范围是
.
C
考点二 二次函数的图象与其系数的关系
名师指导
利用二次函数
的大小关系的方法:
式子 方法
图1
例2 已知抛物线 的图象如图1所
示,则下列结论正确的是( ).
A.
B.
C.
D.( 为任意实数)
图1
提示:因为抛物线开口向下,抛物线与 轴交于正半轴,
所以,.由此可得.因为抛物线与
轴的交点是和 ,所以抛物线的对称轴为直线
,即.从而得 ,所以
, .因为抛物线的对称轴为直线
【答案】D
,且开口向下,所以当时,函数值最大,为 .所
以,即 .
图1
思路点拨 先观察图象,分析,, 的符号.由抛物线
开口向下,得;由抛物线交 轴于正半轴,得
;根据抛物线与 轴的两个交点坐标可确定对称轴,
从而可得关于, 的等式.由此可判断选项A,B,C中
的结论是否正确.对于选项D,比较和 的
大小相当于比较时的函数值和 时的函数值的大小.
考点专练
图2
4.(2023·湖南株洲·中考)如图2,直线 为二次函数
的图象的对称轴,则下列说法
正确的是( ).
C
A.恒大于0 B., 同号
C., 异号 D.以上说法都不对
图3
5.(2024·黑龙江齐齐哈尔·中考)如图3,二次函数
的图象与轴交于 ,
,其中 .结合图象给出下列结论:
;;③当时,随 的增大
而减小;④关于 的一元二次方程
A.2 B.3 C.4 D.5
的另一个根是;的取值范围为 .
其中正确结论的个数是( ).
图3
提示:由函数图象可知,, .又
,所以.所以 .故结论①错误,
结论③正确.由 是函数图象与坐标轴的交点
可知,.则 ,故结论②正
确.由题意知,是方程的两个根,所以 ,
即.由此可得,关于的一元二次方程
的另一个根是.故结论④正确.因为 ,所以
.所以.因为 ,
所以
解得 .故结论⑤正确.
【答案】C
图3
考点三 二次函数图象的平移规律
名师指导
1.二次函数图象的平移规律:左、右平移是横坐标的变化,左移加
右移减;上、下平移是纵坐标的变化,上移加下移减.平移不改变开口
大小和开口方向.
2.二次函数图象的平移问题,关键要抓住顶点位置的变化,只要确
定平移后顶点的坐标,就可以写出平移后抛物线对应的函数解析式.
例3 (2025·镇江·中考模拟)小嘉提出将二次函数 的图象平移或
翻折后经过点 有4种方法:①向右平移2个单位长度;②向右平移1个
单位长度,再向下平移1个单位长度;③向下平移4个单位长度;④沿 轴翻
折,再向上平移4个单位长度.你认为小嘉提出的方法中正确的有( ).
A.1种 B.2种 C.3种 D.4种
提示:向右平移2个单位长度,所得图象对应的函数解析式为
.当时,,所以此时图象经过点 .故方法①符
合题意.向右平移1个单位长度,再向下平移1个单位长度,所得图象对
应的函数解析式为.当时, ,所以此时图象
经过点 .故方法②符合题意.向下平移4个单位长度,所得图象对应的
函数解析式为.当时,,所以此时图象经过点 .
故方法③符合题意.沿轴翻折,所得图象对应的函数解析式为 ,
再向上平移4个单位长度,所得图象对应的函数解析式为 .当
时,,所以此时图象经过点 .故方法④符合题意.
【答案】D
思路点拨 只要根据二次函数图象的平移规律和翻折规律,求出平移或
翻折后图象对应的函数解析式,就可判断点 是否在平移或翻折后的
函数图象上.
考点专练
6.(2025·四川泸州·中考模拟)抛物线 经平移后,不可能
得到的抛物线是( ).
D
A. B.
C. D.
7.(2024·内蒙古包头·中考)将抛物线 向下平移2个单位长度
后,所得新抛物线对应的函数解析式为( ).
D
A. B.
C. D.
8.将抛物线沿 轴翻折,再向右平移3个单位长度后,
所得抛物线的函数解析式是_________________.
考点四 确定二次函数的解析式
名师指导
利用待定系数法确定二次函数的解析式时,可根据给定的条件,选
择恰当的方法设出函数解析式,再代入数值求解.一般地,当已知抛物
线上的三点坐标时,常设为一般式
顶点坐标、对称轴或最大(小)值时,常设为顶点式
当已知抛物线与
例4 下表中与 的数据满足我们初中学过的某种函数关系,其函数解析
式为_______________.
… 0 1 3 …
… 0 3 4 0 …
提示:由表中数据知,当值取,3时, 值均为0,
因此与满足我们学过的二次函数关系.(方法一,设一般式)设 关于
的函数解析式为,将表中,的3组对应值 ,
,代入,得解得所以关于 的函数解
析式为.(方法二,设交点式)因为, 是二
次函数图象与 轴的两个交点,所以可设函数解析式为
… 0 1 3 …
… 0 3 4 0 …
.将代入,得.解得 .
所以关于的函数解析式为,即 .
(方法三,设顶点式)因为二次函数图象与轴的两个交点为 ,
,所以函数图象的对称轴为直线 .又根据表中数据,可
知函数图象的顶点为,故可设函数解析式为 .将
代入,得.解得.所以关于 的函数解析式
为,即 .
【答案】
思路点拨 由表中数据知,当值取,3时, 值均为0,即函数图象与
轴有两个交点.因此与 满足我们学过的二次函数关系,用待定系数法
可求出其函数解析式.设二次函数的解析式时,有一般式、交点式、顶
点式三种方法.
考点专练
9.(2024·浙江·中考节选)已知二次函数(, 为常数)
的图象经过点,对称轴为直线 .
(1)求这个二次函数的解析式.
解:由二次函数的对称轴为直线,得 .
解得.
将代入,得.
解得 .
故这个二次函数的解析式为 .
(2)当时,二次函数 的最大值与最小值的
差为,求 的取值范围.
解:当 时,二次函数 的最大值为5,最小值为.
由此可得,.
解得 ,不符合题意,舍去.
当时,二次函数 的最大值为5,最小值为,且,符合题意.
当 时,二次函数的最大值为,最小值为 .
.
解得, ,不符合题意,舍去.
综上所述,的取值范围为 .
考点五 二次函数与方程、不等式的关系
名师指导
1.二次函数
系:
(1)从“形”的方面看,二次函数
(2)从“数”的方面看,当二次函数
2.二次函数与关于 的不等式 的关系
(1)关于的不等式 的解集,就是二次函数的图象位于直线 上方部分的点的横坐标的取值范围;
(2)关于的不等式 的解集,就是二次函数的图象位于直线 下方部分的点的横坐标的取值范围.
图4
例5 (2025·新疆·中考模拟)如图4,在平面直角坐标系中,
直线与抛物线 相交于点
,.结合图象,判断下列结论:①当 时,
;是方程 的一个解;
③若,是抛物线上的两点,则 ;④
对于抛物线,当时,
A.4个 B.3个 C.2个 D.1个
的取值范围是 .其中正确结论的个数是 ( ).
图4
提示:由图象可知,当时,直线
在抛物线的上方,所以 .故①正
确.由图象可知,抛物线与 轴的一个交
点为,所以是方程 的一个解.
故②正确.将点,代入 ,可解
得,.所以抛物线对应的函数解析式为 .当
时,,当时,,所以 .故③正确.由③可
知点与点 关于抛物线的对称轴对称,从而得抛物线的对称轴
为直线.将代入抛物线解析式得 .当
时,由图象可知,在 处取得最大值,
在处取得最小值,所以 .故④错误.
【答案】B
图4
考点专练
10.二次函数的图象如图5,那么关于 的方程
的根的情况是( ).
A
图5
A.有两个相等的实数根 B.有两个异号的实数根
C.有两个不相等的实数根 D.没有实数根
11.图6是二次函数的部分图象,其对称轴为直线 .
若其与轴的一个交点为,则由图象可知,关于 的方程
的解是________________,关于 的不等式
的解集是_______________.
,
或
图6
第14讲 二次函数的图象和性质
靶向锤炼
靶向练
1.(2025·广西柳州·模拟)下列有关二次函数 的图象说
法不正确的是( ).
C
A.开口向上 B.对称轴是直线
C.顶点坐标是 D.当时,随 增大而减小
2.(2023·广西·中考)将抛物线 先向右平移3个单位长度,再向上
平移4个单位长度,得到的抛物线的函数解析式是( ).
A
A. B.
C. D.
3.(2025·广西河池·模拟)二次函数 的最大值是
( ).
A
A.7 B. C.2 D.
4.(2024·四川凉山·中考)抛物线经过 ,
,,三点,则,, 的大小关系正确的是( ).
D
A. B. C. D.
5.(2024·内蒙古呼和浩特·中考)在同一平面直角坐标系中,函数
和 的图象大致如图1所示,则函数
的图象大致为( ).
D
图1
A. B. C. D.
6.(2025·黑龙江哈尔滨·中考改编)抛物线与 轴的交
点坐标是______,与 轴的交点坐标是______________.
或
图2
7.(2023·浙江宁波·中考)如图2,已知二次函数
的图象经过点和点 .
(1)求该二次函数的解析式及图象的顶点坐标.
解:因为二次函数 的图象经过点
和点,所以 解得
所以该二次函数的解析式为 .
因为,所以图象的顶点坐标为 .
(2)当时,请根据图象直接写出 的取值范围.
图2
提示:如图9,点关于对称轴直线的对称点 的坐标为,所以当时,的取值范围是 .
图9
【答案】
攻坚练
8.(2025·湖南株洲·中考改编)已知二次函数 ,其中
, ,则该函数的图象可能为( ).
C
A. B. C. D.
9.(2024·四川泸州·中考)已知二次函数
的图象只经过第一、二、四象限,
则实数 的取值范围为( ).
A
A. B. C. D.
提示:由图象只经过第一、二、四象限,得抛物线的开口向上,对称轴
在轴右侧,,抛物线与轴有两个交点.所以 ,
,,.解得 .
图3
10.(2024·四川广元·中考)如图3,已知抛物线
过点,与 轴交点的横坐标分
别为,,且, ,给出下列结
论:,②关于 的方程
有两个不相等的实数根,
,, .其中正确的
结论有( ).
A.1个 B.2个 C.3个 D.4个
图3
提示:由图象可知,当时, ,
抛物线与直线 有两个交点,故结论①错误,结论
②正确.由, ,得抛物线的对称
轴,又,所以 .故结
论③错误.抛物线过点,得 .由图象可知,
当时,,即,当 时,
,所以.所以 .故结论④正确.由
,,得,则 .由根与系
数的关系,得.所以 .故结论⑤正确.
【答案】C
图3
图4
11.(2025·湖南娄底·中考改编)如图4,抛物线
与轴相交于点和点 ,
与轴相交于点,点在抛物线上.当 轴
时, ___.
4
提示:因为抛物线与 轴相交于
点和点 ,所以抛物线的对称轴为直线
.因为当时,,即.又轴,所以点 与
点关于对称轴直线对称.所以.所以 .
图5
12.如图5,二次函数( 为常数)的
图象的对称轴为直线 .
(1)求 的值.
解:在中,令 ,得.
解得, .
所以二次函数的图象与轴的交点为
和 .
因为该二次函数的图象的对称轴为直线 ,所以
.解得 .
图5
(2)向下平移该二次函数的图象,使其经过原点,求
平移后的图象所对应的二次函数解析式.
解:由(1)知 ,所以二次函数解析式为
,即 .
.
故将该图象向下平移3个单位长度时,所得图象经过原点.
所以平移后图象所对应的二次函数解析式为 .
拔尖练
13.定义:,例如,,, .
若函数, ,则该函数的最大值为( ).
A.0 B.2 C.3 D.4
图10
提示:根据题意,画出函数 和
的图象,如图10所示.解方
程,得或 .
所以 观
察图象知,当时, 取得最大值,此时
,所以该函数的最大值为3.
【答案】C
图6
14.(2024·江苏镇江·中考)如图6,在平面直角坐
标系中, 为坐标原点,二次函数
的图象与轴交于, 两点
(点在点的左侧),顶点为 .
(1)求,, 三点的坐标.
解:因为二次函数 的图象的顶 点为,所以.
令,解得, .
所以, .
【点击查看解题微课】
图6
(2)一个二次函数的图象经过,, 三点,
其中,该函数图象与轴交于另一点,点 在
线段上(点不与点, 重合).
①若点的坐标为,则 ___.
提示:由题意知,该二次函数图象经过点 ,
.所以该二次函数图象的对称轴为直线 .
因为点,的纵坐标相同,即轴,则点, 关于对
称直线轴对称,所以. 解得 .
②求 的取值范围.
解:设经过点,, 的二次函数的解析式为
,由, 关于对称轴对称,得对称轴为直线 .
所以该二次函数图象的对称轴与轴的交点坐标为,.
因为, 两点关于对称轴直线对称,点 的坐标为,所以.
图6
由点 在线段上,且与点,不重合,得 解得
.
又 ,所以,即.
所以且 .
图6
③求 的最大值.
解:由题意,得, ,所以 .
且,所以当时, 有最大值,最大值为4.
图6
复习讲义
第一篇 考点精讲
专题三 函数
第14讲 二次函数的图象和性质
聚焦核心
1.二次函数的定义
一般地,形如
叫作二次函数.其中
数、一次项系数和常数项.特别地,当
2.二次函数 的图象与性质
图象 ___________________________ ___________________________
开口方向 向上 向下
对称轴
顶点 坐标
增减性
减小
增大
增大
续表
减小
最值
大
续表
小
3.二次函数 的图象与其系数的关系
系数 图象特点
开口向____
开口向____
开口越____
开口越____
对称轴是___轴
上
下
小
大
左
右
系数 图象特点
经过____点
正
原
负
两
一
没有
续表
4.二次函数解析式的三种形式
(1)一般式:,,是常数,且 ,函数图象
与 轴的交点坐标是______.
(2)顶点式:,,是常数,且 ,函数图
象的顶点坐标是______.
(3)交点式:,,是常数,且 ,函
数图象与 轴的两个交点的坐标是_______,_______.
说明:通过配方可以把一般式 化为顶点式
,其中_____, .
第14讲 二次函数的图象和性质
案例分析
考点一 二次函数的图象和性质
名师指导
二次函数的很多性质(对称轴、顶点坐标、最值、增减性等)都可
以从函数解析式的顶点式中反映出来,所以研究二次函数的性质时,通
常将解析式化为顶点式,即
例1 关于二次函数 ,下列说法正确的是( ).
A.该函数图象与轴交于点
B.该函数图象的对称轴为直线
C.该函数图象的顶点坐标为
D.该函数的最大值是3
提示:在中,当时, ,所以该函数图象与
轴交于点 ,故说法A错误.因为
,所以该函数图象的对称轴为直线
,顶点坐标为,故说法B,C错误.因为 ,所以函数
图象开口向下.所以当 时,函数有最大值,最大值为3.故说法D正确.
D
思路点拨 将代入函数解析式,就可以求出函数图象与 轴的交点
坐标.将二次函数的一般式化为顶点式,就可以判断函数图象的对称轴、
顶点坐标和最值.
考点专练
1.(2023·四川甘孜·中考)下列关于二次函数 的说法正
确的是( ).
D
A.图象是一条开口向下的抛物线 B.图象与 轴没有交点
C.当时,随的增大而增大 D.图象的顶点坐标是
2.(2024·广东·中考)若点,,都在二次函数
的图象上,则( ).
A
A. B. C. D.
3.(2025·四川乐山·中考改编)已知二次函数 ,
当时,函数取得最大值;当时,函数取得最小值. 的取值
范围是( ).
A. B. C. D.
提示:因为当时,函数取得最小值,所以在 的范围
内,可取到1,所以.因为二次函数 的对称轴为直线
,所以时的函数值与 时的函数值相等,又因为当
时,函数取得最大值,所以,综上所述, 的取值范围是
.
C
考点二 二次函数的图象与其系数的关系
名师指导
利用二次函数
的大小关系的方法:
式子 方法
图1
例2 已知抛物线 的图象如图1所
示,则下列结论正确的是( ).
A.
B.
C.
D.( 为任意实数)
图1
提示:因为抛物线开口向下,抛物线与 轴交于正半轴,
所以,.由此可得.因为抛物线与
轴的交点是和 ,所以抛物线的对称轴为直线
,即.从而得 ,所以
, .因为抛物线的对称轴为直线
【答案】D
,且开口向下,所以当时,函数值最大,为 .所
以,即 .
图1
思路点拨 先观察图象,分析,, 的符号.由抛物线
开口向下,得;由抛物线交 轴于正半轴,得
;根据抛物线与 轴的两个交点坐标可确定对称轴,
从而可得关于, 的等式.由此可判断选项A,B,C中
的结论是否正确.对于选项D,比较和 的
大小相当于比较时的函数值和 时的函数值的大小.
考点专练
图2
4.(2023·湖南株洲·中考)如图2,直线 为二次函数
的图象的对称轴,则下列说法
正确的是( ).
C
A.恒大于0 B., 同号
C., 异号 D.以上说法都不对
图3
5.(2024·黑龙江齐齐哈尔·中考)如图3,二次函数
的图象与轴交于 ,
,其中 .结合图象给出下列结论:
;;③当时,随 的增大
而减小;④关于 的一元二次方程
A.2 B.3 C.4 D.5
的另一个根是;的取值范围为 .
其中正确结论的个数是( ).
图3
提示:由函数图象可知,, .又
,所以.所以 .故结论①错误,
结论③正确.由 是函数图象与坐标轴的交点
可知,.则 ,故结论②正
确.由题意知,是方程的两个根,所以 ,
即.由此可得,关于的一元二次方程
的另一个根是.故结论④正确.因为 ,所以
.所以.因为 ,
所以
解得 .故结论⑤正确.
【答案】C
图3
考点三 二次函数图象的平移规律
名师指导
1.二次函数图象的平移规律:左、右平移是横坐标的变化,左移加
右移减;上、下平移是纵坐标的变化,上移加下移减.平移不改变开口
大小和开口方向.
2.二次函数图象的平移问题,关键要抓住顶点位置的变化,只要确
定平移后顶点的坐标,就可以写出平移后抛物线对应的函数解析式.
例3 (2025·镇江·中考模拟)小嘉提出将二次函数 的图象平移或
翻折后经过点 有4种方法:①向右平移2个单位长度;②向右平移1个
单位长度,再向下平移1个单位长度;③向下平移4个单位长度;④沿 轴翻
折,再向上平移4个单位长度.你认为小嘉提出的方法中正确的有( ).
A.1种 B.2种 C.3种 D.4种
提示:向右平移2个单位长度,所得图象对应的函数解析式为
.当时,,所以此时图象经过点 .故方法①符
合题意.向右平移1个单位长度,再向下平移1个单位长度,所得图象对
应的函数解析式为.当时, ,所以此时图象
经过点 .故方法②符合题意.向下平移4个单位长度,所得图象对应的
函数解析式为.当时,,所以此时图象经过点 .
故方法③符合题意.沿轴翻折,所得图象对应的函数解析式为 ,
再向上平移4个单位长度,所得图象对应的函数解析式为 .当
时,,所以此时图象经过点 .故方法④符合题意.
【答案】D
思路点拨 只要根据二次函数图象的平移规律和翻折规律,求出平移或
翻折后图象对应的函数解析式,就可判断点 是否在平移或翻折后的
函数图象上.
考点专练
6.(2025·四川泸州·中考模拟)抛物线 经平移后,不可能
得到的抛物线是( ).
D
A. B.
C. D.
7.(2024·内蒙古包头·中考)将抛物线 向下平移2个单位长度
后,所得新抛物线对应的函数解析式为( ).
D
A. B.
C. D.
8.将抛物线沿 轴翻折,再向右平移3个单位长度后,
所得抛物线的函数解析式是_________________.
考点四 确定二次函数的解析式
名师指导
利用待定系数法确定二次函数的解析式时,可根据给定的条件,选
择恰当的方法设出函数解析式,再代入数值求解.一般地,当已知抛物
线上的三点坐标时,常设为一般式
顶点坐标、对称轴或最大(小)值时,常设为顶点式
当已知抛物线与
例4 下表中与 的数据满足我们初中学过的某种函数关系,其函数解析
式为_______________.
… 0 1 3 …
… 0 3 4 0 …
提示:由表中数据知,当值取,3时, 值均为0,
因此与满足我们学过的二次函数关系.(方法一,设一般式)设 关于
的函数解析式为,将表中,的3组对应值 ,
,代入,得解得所以关于 的函数解
析式为.(方法二,设交点式)因为, 是二
次函数图象与 轴的两个交点,所以可设函数解析式为
… 0 1 3 …
… 0 3 4 0 …
.将代入,得.解得 .
所以关于的函数解析式为,即 .
(方法三,设顶点式)因为二次函数图象与轴的两个交点为 ,
,所以函数图象的对称轴为直线 .又根据表中数据,可
知函数图象的顶点为,故可设函数解析式为 .将
代入,得.解得.所以关于 的函数解析式
为,即 .
【答案】
思路点拨 由表中数据知,当值取,3时, 值均为0,即函数图象与
轴有两个交点.因此与 满足我们学过的二次函数关系,用待定系数法
可求出其函数解析式.设二次函数的解析式时,有一般式、交点式、顶
点式三种方法.
考点专练
9.(2024·浙江·中考节选)已知二次函数(, 为常数)
的图象经过点,对称轴为直线 .
(1)求这个二次函数的解析式.
解:由二次函数的对称轴为直线,得 .
解得.
将代入,得.
解得 .
故这个二次函数的解析式为 .
(2)当时,二次函数 的最大值与最小值的
差为,求 的取值范围.
解:当 时,二次函数 的最大值为5,最小值为.
由此可得,.
解得 ,不符合题意,舍去.
当时,二次函数 的最大值为5,最小值为,且,符合题意.
当 时,二次函数的最大值为,最小值为 .
.
解得, ,不符合题意,舍去.
综上所述,的取值范围为 .
考点五 二次函数与方程、不等式的关系
名师指导
1.二次函数
系:
(1)从“形”的方面看,二次函数
(2)从“数”的方面看,当二次函数
2.二次函数与关于 的不等式 的关系
(1)关于的不等式 的解集,就是二次函数的图象位于直线 上方部分的点的横坐标的取值范围;
(2)关于的不等式 的解集,就是二次函数的图象位于直线 下方部分的点的横坐标的取值范围.
图4
例5 (2025·新疆·中考模拟)如图4,在平面直角坐标系中,
直线与抛物线 相交于点
,.结合图象,判断下列结论:①当 时,
;是方程 的一个解;
③若,是抛物线上的两点,则 ;④
对于抛物线,当时,
A.4个 B.3个 C.2个 D.1个
的取值范围是 .其中正确结论的个数是 ( ).
图4
提示:由图象可知,当时,直线
在抛物线的上方,所以 .故①正
确.由图象可知,抛物线与 轴的一个交
点为,所以是方程 的一个解.
故②正确.将点,代入 ,可解
得,.所以抛物线对应的函数解析式为 .当
时,,当时,,所以 .故③正确.由③可
知点与点 关于抛物线的对称轴对称,从而得抛物线的对称轴
为直线.将代入抛物线解析式得 .当
时,由图象可知,在 处取得最大值,
在处取得最小值,所以 .故④错误.
【答案】B
图4
考点专练
10.二次函数的图象如图5,那么关于 的方程
的根的情况是( ).
A
图5
A.有两个相等的实数根 B.有两个异号的实数根
C.有两个不相等的实数根 D.没有实数根
11.图6是二次函数的部分图象,其对称轴为直线 .
若其与轴的一个交点为,则由图象可知,关于 的方程
的解是________________,关于 的不等式
的解集是_______________.
,
或
图6
第14讲 二次函数的图象和性质
靶向锤炼
靶向练
1.(2025·广西柳州·模拟)下列有关二次函数 的图象说
法不正确的是( ).
C
A.开口向上 B.对称轴是直线
C.顶点坐标是 D.当时,随 增大而减小
2.(2023·广西·中考)将抛物线 先向右平移3个单位长度,再向上
平移4个单位长度,得到的抛物线的函数解析式是( ).
A
A. B.
C. D.
3.(2025·广西河池·模拟)二次函数 的最大值是
( ).
A
A.7 B. C.2 D.
4.(2024·四川凉山·中考)抛物线经过 ,
,,三点,则,, 的大小关系正确的是( ).
D
A. B. C. D.
5.(2024·内蒙古呼和浩特·中考)在同一平面直角坐标系中,函数
和 的图象大致如图1所示,则函数
的图象大致为( ).
D
图1
A. B. C. D.
6.(2025·黑龙江哈尔滨·中考改编)抛物线与 轴的交
点坐标是______,与 轴的交点坐标是______________.
或
图2
7.(2023·浙江宁波·中考)如图2,已知二次函数
的图象经过点和点 .
(1)求该二次函数的解析式及图象的顶点坐标.
解:因为二次函数 的图象经过点
和点,所以 解得
所以该二次函数的解析式为 .
因为,所以图象的顶点坐标为 .
(2)当时,请根据图象直接写出 的取值范围.
图2
提示:如图9,点关于对称轴直线的对称点 的坐标为,所以当时,的取值范围是 .
图9
【答案】
攻坚练
8.(2025·湖南株洲·中考改编)已知二次函数 ,其中
, ,则该函数的图象可能为( ).
C
A. B. C. D.
9.(2024·四川泸州·中考)已知二次函数
的图象只经过第一、二、四象限,
则实数 的取值范围为( ).
A
A. B. C. D.
提示:由图象只经过第一、二、四象限,得抛物线的开口向上,对称轴
在轴右侧,,抛物线与轴有两个交点.所以 ,
,,.解得 .
图3
10.(2024·四川广元·中考)如图3,已知抛物线
过点,与 轴交点的横坐标分
别为,,且, ,给出下列结
论:,②关于 的方程
有两个不相等的实数根,
,, .其中正确的
结论有( ).
A.1个 B.2个 C.3个 D.4个
图3
提示:由图象可知,当时, ,
抛物线与直线 有两个交点,故结论①错误,结论
②正确.由, ,得抛物线的对称
轴,又,所以 .故结
论③错误.抛物线过点,得 .由图象可知,
当时,,即,当 时,
,所以.所以 .故结论④正确.由
,,得,则 .由根与系
数的关系,得.所以 .故结论⑤正确.
【答案】C
图3
图4
11.(2025·湖南娄底·中考改编)如图4,抛物线
与轴相交于点和点 ,
与轴相交于点,点在抛物线上.当 轴
时, ___.
4
提示:因为抛物线与 轴相交于
点和点 ,所以抛物线的对称轴为直线
.因为当时,,即.又轴,所以点 与
点关于对称轴直线对称.所以.所以 .
图5
12.如图5,二次函数( 为常数)的
图象的对称轴为直线 .
(1)求 的值.
解:在中,令 ,得.
解得, .
所以二次函数的图象与轴的交点为
和 .
因为该二次函数的图象的对称轴为直线 ,所以
.解得 .
图5
(2)向下平移该二次函数的图象,使其经过原点,求
平移后的图象所对应的二次函数解析式.
解:由(1)知 ,所以二次函数解析式为
,即 .
.
故将该图象向下平移3个单位长度时,所得图象经过原点.
所以平移后图象所对应的二次函数解析式为 .
拔尖练
13.定义:,例如,,, .
若函数, ,则该函数的最大值为( ).
A.0 B.2 C.3 D.4
图10
提示:根据题意,画出函数 和
的图象,如图10所示.解方
程,得或 .
所以 观
察图象知,当时, 取得最大值,此时
,所以该函数的最大值为3.
【答案】C
图6
14.(2024·江苏镇江·中考)如图6,在平面直角坐
标系中, 为坐标原点,二次函数
的图象与轴交于, 两点
(点在点的左侧),顶点为 .
(1)求,, 三点的坐标.
解:因为二次函数 的图象的顶 点为,所以.
令,解得, .
所以, .
【点击查看解题微课】
图6
(2)一个二次函数的图象经过,, 三点,
其中,该函数图象与轴交于另一点,点 在
线段上(点不与点, 重合).
①若点的坐标为,则 ___.
提示:由题意知,该二次函数图象经过点 ,
.所以该二次函数图象的对称轴为直线 .
因为点,的纵坐标相同,即轴,则点, 关于对
称直线轴对称,所以. 解得 .
②求 的取值范围.
解:设经过点,, 的二次函数的解析式为
,由, 关于对称轴对称,得对称轴为直线 .
所以该二次函数图象的对称轴与轴的交点坐标为,.
因为, 两点关于对称轴直线对称,点 的坐标为,所以.
图6
由点 在线段上,且与点,不重合,得 解得
.
又 ,所以,即.
所以且 .
图6
③求 的最大值.
解:由题意,得, ,所以 .
且,所以当时, 有最大值,最大值为4.
图6
同课章节目录
