2026年中考《数学》复习课件 专题三 函数--第16讲 与二次函数有关的综合题(共73张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件 专题三 函数--第16讲 与二次函数有关的综合题(共73张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 09:50:41 | ||
图片预览











文档简介
(共73张PPT)
复习讲义
第一篇 考点精讲
专题三 函数
第16讲 与二次函数有关的综合题
聚焦核心
1.最值问题:以二次函数为背景,求某个量的最值,一般可以转化为求
二次函数的最值.将二次函数化为顶点式 ,结合实际问
题,确定自变量的取值范围,若可取的值,则当时, ___为
函数的最____值;当, ___为函数的最____值.
小
大
2.表示点坐标:(1)函数图象上的点满足函数解析式,两函数图象的
交点同时满足这两个函数解析式;(2)垂直于轴(平行于 轴)的直
线上的点的____坐标相等;(3)垂直于轴(平行于 轴)的直线上的
点的____坐标相等.
横
纵
3.表示线段长:(1)与 轴垂直的线段的长可用两端点的纵坐标相减
(上减下)表示;(2)与 轴垂直的线段长可用两端点的横坐标相减
(右减左)表示;(3)不与坐标轴垂直的线段的长,过线段端点分别
作轴、 轴的垂线构造直角三角形,运用勾股定理或结合相似三角形可
求得线段长.
第16讲 与二次函数有关的综合题
案例分析
考点一 二次函数的探究类问题
名师指导
二次函数探究类问题,通常会给出部分
二次函数的性质,结合二次函数的图象,可以更加直观地归纳出关于二
次函数的性质和结论.此类问题有利于培养学生的推理能力.
例1 (2024·广西·中考)课堂上,数学老师组织同学们围绕关于 的二次
函数 的最值问题展开探究.
【经典回顾】二次函数求最值的方法.
(1)老师给出,求二次函数 的最小值.
①请你写出对应的函数解析式.
解:将代入 ,得.
所以 .
②求当取何值时,函数有最小值,并写出此时的 值.
解:,故当时, 有最小值,最小值为 .
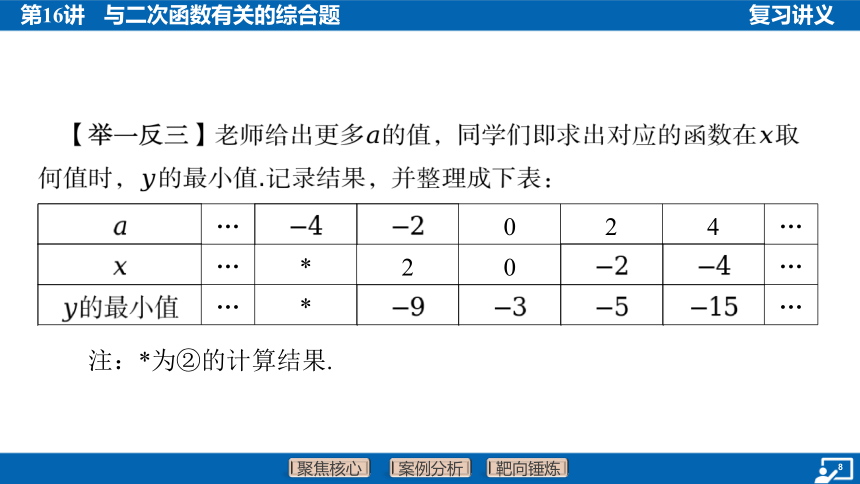
【举一反三】老师给出更多的值,同学们即求出对应的函数在 取
何值时, 的最小值.记录结果,并整理成下表:
… 0 2 4 …
… * 2 0 …
… * …
注:*为②的计算结果.
【探究发现】老师:“请同学们结合学过的函数知识,观察表格,
谈谈你的发现.”
甲同学:“我发现,老师给了值后,我们只要取 ,就能得到
的最小值.”
乙同学:“我发现,的最小值随值的变化而变化,当 由小变大
时,的最小值先增大后减小,所以我猜想 的最小值中存在最大值.”
(2)请结合函数解析式 ,解释甲同学的说法是否
合理?
解:,关于 的二次函数的图象的开口向上,对称轴为直线,所以当时, 有最小值.
故甲同学的说法是合理的.
(3)你认为乙同学的猜想是否正确?若正确,则请求出此最大值;若
不正确,则请说明理由.
解:乙同学的猜想是正确的.
由(2)可知,当时, 有最小值,.
由 ,得.
所以的最小值中存在最大值,最大值为 .
思路点拨(1)将 的值代入,得到二次函数的解析式,再将其化为顶点
式,即可得到的最值及对应的的值.(2)把 看作常数,将二次函数
的解析式化为顶点式,由此可探究甲同学的说法是否合理.(3)结合
(2)中结论,得到的最小值关于 的函数解析式,再由该解析式的特
点分析其性质.
考点专练
1.(2025·黑龙江大庆·模拟)某班数学兴趣小组对函数 的
图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数,与 的几组对应值列表如下:
… 0 1 2 3 …
… 3 0 0 3 …
其中, ___.
0
(2)如图1,描出表格中的点,用光滑的曲线顺次连接 轴左边各点和
原点,观察函数图象,画出该函数图象的另一部分,并思考:当
________时,函数有最小值.
或1
图1
解:作图如图17.
图17
(3)进一步探究函数图象发现:
①函数图象与轴有___个交点,所以方程 有___个实数根;
②方程 有___个实数根;
3
提示:观察图象,可知函数的图象与直线 有2个交点.
③关于的方程有4个实数根时, 的取值范围是_________
_____.
图18
提示:观察图象,可知当时,直线
与函数 的图象有4个交点.
考点二 与二次函数有关的平移、对称、旋转变换问题
名师指导
二次函数背景下的平移、对称、旋转变换问题涉及的知识面较广,
综合性较强.常涉及一元二次方程、相似三角形、勾股定理等相关知识;
常运用的数学思想方法有数形结合思想、方程思想等.
图2
例2 如图2,在平面直角坐标系中, 为坐标原点,
抛物线与轴交于点,与 轴正半轴
交于点,连接,将 向右上方平移,得到
,且点, 落在抛物线的对称轴上,点
落在抛物线上,则直线 对应的函数解析式为
( ).
A. B. C. D.
图2
提示:令,得.解得 ,
.令,得.所以, .因为抛
物线的对称轴为直线 ,所以
设,则,因为点 落在抛物线上,所
以.解得.所以, .
【答案】B
设直线对应的函数解析式为 ,将点
,代入,得解得 所以
直线对应的函数解析式为 .
图2
思路点拨 要求直线 对应的函数解析式,需要求
出点, 的坐标.根据二次函数的解析式可求出点
, 的坐标,再结合平移前后点的坐标变化规律和
点的位置特征得到点, 的坐标.
考点专练
2.将抛物线绕原点旋转 ,则旋转后的抛物线对应的函
数解析式为( ).
D
A. B. C. D.
提示:抛物线的顶点坐标为,将点绕原点 旋转
,得到点,因此旋转后的抛物线的顶点坐标为 .又因
为旋转后抛物线的开口方向相反,所以旋转后的抛物线对应的函数解析
式为 .
图3
3.(2025·广东汕头·模拟)如图3,在平面直角坐标系
中,二次函数的图象与轴, 轴分
别交于点,,,且是二次函数图象的顶点.若 是
轴上一个动点,则 的最小值为______.
提示:当时,.所以点 .因为
,所以点. 如图18,作点 关
于轴的对称点,连接,,,则.所以 .所以
.所以当,,三点共线时 的值最小,即
的值最小,最小值为 .
【点击查看网络画板】
4.如图4,在平面直角坐标系中,已知点,,连接 .若二
次函数的图象向上平移 个单位长度时,与线
段有一个公共点,则 的取值范围为__________________.
图4
图4
提示:二次函数的图象向上平移 个
单位长度后对应的函数解析式为
.所以平移
后的抛物线的顶点坐标为 .①当顶点在线段
上时,,解得 .②当向上平移后的抛
物线经过点时,,解得 .③当向
上平移后的抛物线经过点时,,解得 .
所以当或时,二次函数图象与线段 有一个公共点.
或
考点三 二次函数与几何综合问题
名师指导
二次函数通常与线段、特殊三角形、特殊四边形等几何图形综合考
查.对于二次函数
为
表示出几何图形相关的线段长,再结合几何图形的性质列出方程或构建
函数模型求解.
例3 如图5,在平面直角坐标系中,二次函数 的图象与
轴交于,两点,与轴交于点,点在原点的左侧,点 的坐
标为.点是抛物线上的一个动点,且在直线 的上方.
图5
【点击查看网络画板】
【点击查看解题微课】
(1)求这个二次函数的解析式.
图5
解:将,代入,得 解得
所以二次函数的解析式为 .
(2)连接,,并把沿翻折,得到四边形 ,那么是
否存在点,使四边形为菱形?若存在,则请求出此时点 的坐标;
若不存在,则请说明理由.
图5
图15
解:存在点,使四边形 为菱形.
如图15,连接.
设点 的坐标为,交于点
四边形是菱形, .
.
解得 ,(不合题意,舍去)
点 的坐标为 .
(3)当点运动到什么位置时,四边形 的面积最大?求出此时点
的坐标和四边形 的最大面积.
图5
图16
解:如图16,过点作轴的平行线与 交于点,与交于点,连接,,设点 的横坐标为,则, .
由,,得,,直线 的函数解析式为, 点的坐标为
.
由 ,解得,
.
, 当时,四边形的面积最大,此时点 的坐标为,四边形的最大面积为 .
图16
思路点拨(1)将点,的坐标代入,即可求得, 的值.
(2)先假设存在点,使得四边形为菱形.要求点 的坐标,可先设点的横坐标为,由点在抛物线上,可用含 的代数式表示出点 的纵坐标.观察图形可发现, 是菱形 ′ 的对角线,且 在 轴上,结合菱形的两条对角线互相垂直平分,可列出关于 的方程.
(3)观察图形可得S四边形ABPC=S ABC+S BPC,其中A,B,C是定点,则
ABC的面积是定值,可同(2)设出点P的坐标﹐用含m 的式子表示出
S BPC ,再根据式子的特点求出最值.
考点专练
图6
5.如图6,抛物线与轴交于,
两点(点在点的左侧),与轴交于点.直线
与抛物线交于,两点,与轴交于点,点 的
坐标为 .
(1)请直接写出,两点的坐标及直线 对应的
函数解析式.
解:,,直线对应的函数解析式为 .
(2)若是抛物线上的点,点的横坐标为,过点作
轴,垂足为点与直线交于点,当是线段 的三等分点时,求
点 的坐标.
图6
解:根据题意,得, ,, ,则 ,, .
当是线段 的三等分点时,分两种情况讨论.
①当 时,,解得 ,(不合题意,舍去).
当 时,.
所以点的坐标为 .②当 时,
.
解得,(不合题意,舍去).
图6
当 时,.
所以点的坐标为 ,.
综上所述,当是线段的三等分点时,点的坐标为或, .
图6
图7
6.(2025·山东济宁·模拟)如图7,顶点坐标为
的抛物线与轴交于, 两点
(点在点的左侧),与轴交于点, 是直
线上方抛物线上的一个动点,连接 交抛物线
的对称轴于点 .
(1)求抛物线对应的函数解析式.
解:由抛物线的顶点坐标为,可设,将 代
入,得,解得 .
所以抛物线对应的函数解析式为,即 .
图7
(2)连接,当的周长最小时,求点 的坐
标.
解:当点为点 关于抛物线对称轴的对称点时,由交抛物线的对称轴于点,得 ,则 的周长= .
因此 的周长取得最小值.
因为抛物线的对称轴为直线,点,所以点的坐标为 .
(3)过点作轴于点,交直线于点,连接.在点 的运
动过程中,是否存在为等腰三角形?若存在,则求点 的坐标;
若不存在,则请说明理由.
图7
解:存在.
令,则 .
解得,.
所以,.
设直线 对应的函数解析式为,将, 代入,得解得
图7
所以直线 对应的函数解析式为.设点,又 ,,所以,, .
当为等腰三角形时,分三种情况讨论.
①当 时,1,解得
, (不合题意,舍去).
此时点的坐标为.
②当 时,,解得, (不合题意,舍去).此时点的坐标为
当 时,,解得.此时点 的坐标为.
综上所述,点的坐标为 或或 .
图7
第16讲 与二次函数有关的综合题
靶向锤炼
靶向练
1.在平面直角坐标系中,抛物线与轴交于点 ,则与该
抛物线关于点 成中心对称的抛物线对应的函数解析式为( ).
A. B.
C. D.
提示: 因为 ,所以抛物线
的顶点坐标为.当时,,所以 .因为
原抛物线与新抛物线关于点C成中心对称,所以新抛物线的顶点坐标为
.因此新抛物线对应的函数解析式为 ,即
.
A
图1
2.如图1,点,的坐标分别为和 ,抛
物线的顶点在线段 上运动(抛物线随顶点一起平移),
与轴交于,两点(点在点的左侧),点 的横坐标
的最大值为3,则点 的横坐标的最小值为____.
提示:当顶点在点处时,点的横坐标最大,此时,
两点的水平距离为4.由抛物线的对称性可知,, 两点的水平距离也为
4,所以.当顶点在点处时,点的横坐标最小,所以点 的横坐
标的最小值为 .
【点击查看网络画板】
图2
3.(2025·广西柳州·模拟)如图2,在平面直角坐标系
中,二次函数的图象与轴交于,
两点,点的坐标为,与轴交于点 ,
点 为抛物线的顶点.
(1)求这个二次函数的解析式.
解:将,代入 ,得
解得
故这个二次函数的解析式为 .
图2
(2)求 的面积.
解:由(1)知, .
所以.
当时, ,解得,.所以.
所以 .
故 .
攻坚练
4.把二次函数的图象作关于 轴的对称变换,所
得图象的函数解析式为.若 ,
则 的最大值是( ).
A. B.0 C.2 D.6
提示:因为把二次函数的图象作关于 轴的对称变换,所得图象的函数解析式为 ,所以原二次函数图象的顶点坐标为 ,即原二次函数.所以, .由,得.又 ,所以,即.所以 的最大值是6.
【答案】D
图3
5.边长为1的正方形的顶点在 轴的正半轴上,
如图3,将正方形绕顶点顺时针旋转 得
到正方形,使点恰好落在函数
的图象上,则 的值为_ ____.
提示:连接,过点作轴于点 .由题意,得 .因为 ,所以 .因为 ,所以
.所以, .所以,.将,代入 中,得.解得 .
图4
6.(2023·四川巴中·中考)如图4,在平面直角坐标系中,
抛物线经过点和点 ,
其顶点的横坐标为1.
(1)求抛物线对应的函数解析式.
解: 抛物线的顶点的横坐标为1, 对称轴为直线 .
又 抛物线经过点, 抛物线与 轴的另一交点为
设抛物线的对应函数解析式为.
将 代入,解得
抛物线对应的函数解析式为 .
(2)若直线与轴交于点,在第一象限内与抛物线交于点 ,当取何值时, 有最大值?并求出最大值.
图4
解 直线与轴交于点,与抛物线交于点 ,
,
点在第一象限, ,,
.
, 当时,有最大值,最大值为 .
图4
(3)若为抛物线 的对称轴上的
一个动点,将抛物线向左平移1个单位长度后, 为平移
后抛物线上的一个动点.在(2)的条件下求得的点 ,
是否能与点,, 构成平行四边形?若能构成,则请求
出点 的坐标;若不能构成,则请说明理由.
图12
解: , 向左平移1个单位长度后的抛物线对应的函数解析式为.
如图12,由(2)知,已知 ,设,
设存在以,,, 为顶点的平行四边形.
①当以为对角线时, 平行四边形的对角线互相平分,
.
解得
点 在抛物线上, .
点的坐标为
②当以为对角线时,同理可得, .
解得. . 点的坐标为
③当以 为对角线时,同理可得.
解得. .
点的坐标为.
综上所述,存在以,,, 为顶点的平行四边形,点的坐标为
或 或 .
图12
7.(2025·湖南衡阳·中考模拟)如图5,已知抛物线交 轴于
,两点,将该抛物线位于轴下方的部分沿 轴翻折,其余部分不变,
得到的新图象记为“图象”,图象交轴于点 .
图5
图5
(1)写出图象位于线段 上方部分对应的函数解析式.
解:当时,, .
当 时,,解得,
∴ , .
设图象位于线段 上方部分对应的函数解析式为,将 代入,得
∴ 图象 位于线段上方部分对应的函数解析式为
.
图5
(2)当直线与图象 有三个交点时,请结
合图象,直接写出 的值.
提示:由图象得,直线与图象 有三个交
点时,存在两种情况:①当直线过点
时,与图象有三个交点,此时 ;②当直线
与图象位于线段 上方部分相切时,
【答案】 的值是2或3.
图13
与图象有三个交点,如图13,由 ,得 .由,得 .综上所述, 的值是2或3.
(3)为轴正半轴上的一个动点,过点作轴交直线于点 ,
交图象于点.是否存在这样的点,使与 相似?若存在,
则求出所有符合条件的点 的坐标;若不存在,请说明理由.
图5
解:存在满足条件的点
, , 是等腰直角三角形.
①如图14,当,且点在点 左侧时,,此时点与点关于对称轴直线对称, 点的横坐标为
.
图14
图15
②如图15,当,且点 在点右侧时,,此时点的纵坐标为2.由 ,
解得,(舍去)
点的横坐标为.
如图16,当 时, ,此时直线的函数解析式为,联立方程组 解得,(舍去)
点的横坐标为.
.
综上所述,点的坐标为或 或.
图16
8.(2023·湖南益阳·中考)在平面直角坐标系中,直线
与轴交于点,与抛物线交于, 两点(点在点 的左边).
(1)求点 的坐标.
解:令,得, 点的坐标为 .
(2)如图6,若点关于轴的对称点为,当以,, 为顶点的三角形是直角三角形时,求实数 的值.
图6
解:联立直线与抛物线 的函数解析式,得
或
,
点关于 轴的对称点为,
图6
,
.
若 ,则,即, (负值已舍去).
若 ,则 ,即, (负值已舍去).
若 ,则 ,即
,此方程无解.
综上可知,或 .
图7
(3)定义:将平面直角坐标系中横坐标与纵坐标均
为整数的点叫作格点,如, 等均为格
点.如图7,直线与抛物线 所围成的封闭图形即阴
影部分(不包含边界)中的格点数恰好是26个,求
的取值范围.
图17
解:如图17, 直线与抛物线交于点, ,点的横坐标为,点的横坐标为2, 直线 与抛物线 所围成的封闭图形(不包含边界)中的格点只能落在轴和直线上.
,,,
格点数恰好是26个, 落在轴和直线 上的格点数应
各为13个.
点的纵坐标应满足,即 .
①若,即,则线段上的格点应该为, , ,, 点 的纵坐标应满足,即.
若,则,,则线段 上的格点
正好为13个.
综上所述,或 .
图17
靶向练
图8
9.(2024·广东深圳·中考节选)在综合实践课上,数学探
究小组用两个互相垂直的直尺制作了一个“ ”形尺,并用
它对二次函数图象的相关性质进行研究.把“ ”形尺按图8
的方式摆放,水平宽的中点为,图象的顶点为 ,测
得为时,为 .
(1)探究小组先对的图象进行多次测量,测得与 的部分
数据如下表:
0 2 3 4 5 6 …
0 1 2.25 4 6.25 9 …
描点:以表中各组对应值为点的坐标,在图9的平面直角坐标系内描出相应的点.
图8
【猜想】
图9
连线:用光滑的曲线顺次连接各点.
猜想:与 的函数解析式是_________.
解:描点连线绘制函数图象如图18.
图18
提示:由题意,得,.将点 的坐标代入
函数,得 .
【验证】
(2)探究小组又对多个二次函数的图象进行了测量研究,发现测得的
与 也存在类似的函数解析式,并针对二次函数
的情况进行了推理验证.请从下表中任选一种
方法(在“□”内画“√”)并补全其推理过程.(根据需要,选用字母 ,
,,, 表示答案)
□方法1 □方法2
,
,
图10
图11
□方法1 □方法2
图10
图11
续表
复习讲义
第一篇 考点精讲
专题三 函数
第16讲 与二次函数有关的综合题
聚焦核心
1.最值问题:以二次函数为背景,求某个量的最值,一般可以转化为求
二次函数的最值.将二次函数化为顶点式 ,结合实际问
题,确定自变量的取值范围,若可取的值,则当时, ___为
函数的最____值;当, ___为函数的最____值.
小
大
2.表示点坐标:(1)函数图象上的点满足函数解析式,两函数图象的
交点同时满足这两个函数解析式;(2)垂直于轴(平行于 轴)的直
线上的点的____坐标相等;(3)垂直于轴(平行于 轴)的直线上的
点的____坐标相等.
横
纵
3.表示线段长:(1)与 轴垂直的线段的长可用两端点的纵坐标相减
(上减下)表示;(2)与 轴垂直的线段长可用两端点的横坐标相减
(右减左)表示;(3)不与坐标轴垂直的线段的长,过线段端点分别
作轴、 轴的垂线构造直角三角形,运用勾股定理或结合相似三角形可
求得线段长.
第16讲 与二次函数有关的综合题
案例分析
考点一 二次函数的探究类问题
名师指导
二次函数探究类问题,通常会给出部分
二次函数的性质,结合二次函数的图象,可以更加直观地归纳出关于二
次函数的性质和结论.此类问题有利于培养学生的推理能力.
例1 (2024·广西·中考)课堂上,数学老师组织同学们围绕关于 的二次
函数 的最值问题展开探究.
【经典回顾】二次函数求最值的方法.
(1)老师给出,求二次函数 的最小值.
①请你写出对应的函数解析式.
解:将代入 ,得.
所以 .
②求当取何值时,函数有最小值,并写出此时的 值.
解:,故当时, 有最小值,最小值为 .
【举一反三】老师给出更多的值,同学们即求出对应的函数在 取
何值时, 的最小值.记录结果,并整理成下表:
… 0 2 4 …
… * 2 0 …
… * …
注:*为②的计算结果.
【探究发现】老师:“请同学们结合学过的函数知识,观察表格,
谈谈你的发现.”
甲同学:“我发现,老师给了值后,我们只要取 ,就能得到
的最小值.”
乙同学:“我发现,的最小值随值的变化而变化,当 由小变大
时,的最小值先增大后减小,所以我猜想 的最小值中存在最大值.”
(2)请结合函数解析式 ,解释甲同学的说法是否
合理?
解:,关于 的二次函数的图象的开口向上,对称轴为直线,所以当时, 有最小值.
故甲同学的说法是合理的.
(3)你认为乙同学的猜想是否正确?若正确,则请求出此最大值;若
不正确,则请说明理由.
解:乙同学的猜想是正确的.
由(2)可知,当时, 有最小值,.
由 ,得.
所以的最小值中存在最大值,最大值为 .
思路点拨(1)将 的值代入,得到二次函数的解析式,再将其化为顶点
式,即可得到的最值及对应的的值.(2)把 看作常数,将二次函数
的解析式化为顶点式,由此可探究甲同学的说法是否合理.(3)结合
(2)中结论,得到的最小值关于 的函数解析式,再由该解析式的特
点分析其性质.
考点专练
1.(2025·黑龙江大庆·模拟)某班数学兴趣小组对函数 的
图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数,与 的几组对应值列表如下:
… 0 1 2 3 …
… 3 0 0 3 …
其中, ___.
0
(2)如图1,描出表格中的点,用光滑的曲线顺次连接 轴左边各点和
原点,观察函数图象,画出该函数图象的另一部分,并思考:当
________时,函数有最小值.
或1
图1
解:作图如图17.
图17
(3)进一步探究函数图象发现:
①函数图象与轴有___个交点,所以方程 有___个实数根;
②方程 有___个实数根;
3
提示:观察图象,可知函数的图象与直线 有2个交点.
③关于的方程有4个实数根时, 的取值范围是_________
_____.
图18
提示:观察图象,可知当时,直线
与函数 的图象有4个交点.
考点二 与二次函数有关的平移、对称、旋转变换问题
名师指导
二次函数背景下的平移、对称、旋转变换问题涉及的知识面较广,
综合性较强.常涉及一元二次方程、相似三角形、勾股定理等相关知识;
常运用的数学思想方法有数形结合思想、方程思想等.
图2
例2 如图2,在平面直角坐标系中, 为坐标原点,
抛物线与轴交于点,与 轴正半轴
交于点,连接,将 向右上方平移,得到
,且点, 落在抛物线的对称轴上,点
落在抛物线上,则直线 对应的函数解析式为
( ).
A. B. C. D.
图2
提示:令,得.解得 ,
.令,得.所以, .因为抛
物线的对称轴为直线 ,所以
设,则,因为点 落在抛物线上,所
以.解得.所以, .
【答案】B
设直线对应的函数解析式为 ,将点
,代入,得解得 所以
直线对应的函数解析式为 .
图2
思路点拨 要求直线 对应的函数解析式,需要求
出点, 的坐标.根据二次函数的解析式可求出点
, 的坐标,再结合平移前后点的坐标变化规律和
点的位置特征得到点, 的坐标.
考点专练
2.将抛物线绕原点旋转 ,则旋转后的抛物线对应的函
数解析式为( ).
D
A. B. C. D.
提示:抛物线的顶点坐标为,将点绕原点 旋转
,得到点,因此旋转后的抛物线的顶点坐标为 .又因
为旋转后抛物线的开口方向相反,所以旋转后的抛物线对应的函数解析
式为 .
图3
3.(2025·广东汕头·模拟)如图3,在平面直角坐标系
中,二次函数的图象与轴, 轴分
别交于点,,,且是二次函数图象的顶点.若 是
轴上一个动点,则 的最小值为______.
提示:当时,.所以点 .因为
,所以点. 如图18,作点 关
于轴的对称点,连接,,,则.所以 .所以
.所以当,,三点共线时 的值最小,即
的值最小,最小值为 .
【点击查看网络画板】
4.如图4,在平面直角坐标系中,已知点,,连接 .若二
次函数的图象向上平移 个单位长度时,与线
段有一个公共点,则 的取值范围为__________________.
图4
图4
提示:二次函数的图象向上平移 个
单位长度后对应的函数解析式为
.所以平移
后的抛物线的顶点坐标为 .①当顶点在线段
上时,,解得 .②当向上平移后的抛
物线经过点时,,解得 .③当向
上平移后的抛物线经过点时,,解得 .
所以当或时,二次函数图象与线段 有一个公共点.
或
考点三 二次函数与几何综合问题
名师指导
二次函数通常与线段、特殊三角形、特殊四边形等几何图形综合考
查.对于二次函数
为
表示出几何图形相关的线段长,再结合几何图形的性质列出方程或构建
函数模型求解.
例3 如图5,在平面直角坐标系中,二次函数 的图象与
轴交于,两点,与轴交于点,点在原点的左侧,点 的坐
标为.点是抛物线上的一个动点,且在直线 的上方.
图5
【点击查看网络画板】
【点击查看解题微课】
(1)求这个二次函数的解析式.
图5
解:将,代入,得 解得
所以二次函数的解析式为 .
(2)连接,,并把沿翻折,得到四边形 ,那么是
否存在点,使四边形为菱形?若存在,则请求出此时点 的坐标;
若不存在,则请说明理由.
图5
图15
解:存在点,使四边形 为菱形.
如图15,连接.
设点 的坐标为,交于点
四边形是菱形, .
.
解得 ,(不合题意,舍去)
点 的坐标为 .
(3)当点运动到什么位置时,四边形 的面积最大?求出此时点
的坐标和四边形 的最大面积.
图5
图16
解:如图16,过点作轴的平行线与 交于点,与交于点,连接,,设点 的横坐标为,则, .
由,,得,,直线 的函数解析式为, 点的坐标为
.
由 ,解得,
.
, 当时,四边形的面积最大,此时点 的坐标为,四边形的最大面积为 .
图16
思路点拨(1)将点,的坐标代入,即可求得, 的值.
(2)先假设存在点,使得四边形为菱形.要求点 的坐标,可先设点的横坐标为,由点在抛物线上,可用含 的代数式表示出点 的纵坐标.观察图形可发现, 是菱形 ′ 的对角线,且 在 轴上,结合菱形的两条对角线互相垂直平分,可列出关于 的方程.
(3)观察图形可得S四边形ABPC=S ABC+S BPC,其中A,B,C是定点,则
ABC的面积是定值,可同(2)设出点P的坐标﹐用含m 的式子表示出
S BPC ,再根据式子的特点求出最值.
考点专练
图6
5.如图6,抛物线与轴交于,
两点(点在点的左侧),与轴交于点.直线
与抛物线交于,两点,与轴交于点,点 的
坐标为 .
(1)请直接写出,两点的坐标及直线 对应的
函数解析式.
解:,,直线对应的函数解析式为 .
(2)若是抛物线上的点,点的横坐标为,过点作
轴,垂足为点与直线交于点,当是线段 的三等分点时,求
点 的坐标.
图6
解:根据题意,得, ,, ,则 ,, .
当是线段 的三等分点时,分两种情况讨论.
①当 时,,解得 ,(不合题意,舍去).
当 时,.
所以点的坐标为 .②当 时,
.
解得,(不合题意,舍去).
图6
当 时,.
所以点的坐标为 ,.
综上所述,当是线段的三等分点时,点的坐标为或, .
图6
图7
6.(2025·山东济宁·模拟)如图7,顶点坐标为
的抛物线与轴交于, 两点
(点在点的左侧),与轴交于点, 是直
线上方抛物线上的一个动点,连接 交抛物线
的对称轴于点 .
(1)求抛物线对应的函数解析式.
解:由抛物线的顶点坐标为,可设,将 代
入,得,解得 .
所以抛物线对应的函数解析式为,即 .
图7
(2)连接,当的周长最小时,求点 的坐
标.
解:当点为点 关于抛物线对称轴的对称点时,由交抛物线的对称轴于点,得 ,则 的周长= .
因此 的周长取得最小值.
因为抛物线的对称轴为直线,点,所以点的坐标为 .
(3)过点作轴于点,交直线于点,连接.在点 的运
动过程中,是否存在为等腰三角形?若存在,则求点 的坐标;
若不存在,则请说明理由.
图7
解:存在.
令,则 .
解得,.
所以,.
设直线 对应的函数解析式为,将, 代入,得解得
图7
所以直线 对应的函数解析式为.设点,又 ,,所以,, .
当为等腰三角形时,分三种情况讨论.
①当 时,1,解得
, (不合题意,舍去).
此时点的坐标为.
②当 时,,解得, (不合题意,舍去).此时点的坐标为
当 时,,解得.此时点 的坐标为.
综上所述,点的坐标为 或或 .
图7
第16讲 与二次函数有关的综合题
靶向锤炼
靶向练
1.在平面直角坐标系中,抛物线与轴交于点 ,则与该
抛物线关于点 成中心对称的抛物线对应的函数解析式为( ).
A. B.
C. D.
提示: 因为 ,所以抛物线
的顶点坐标为.当时,,所以 .因为
原抛物线与新抛物线关于点C成中心对称,所以新抛物线的顶点坐标为
.因此新抛物线对应的函数解析式为 ,即
.
A
图1
2.如图1,点,的坐标分别为和 ,抛
物线的顶点在线段 上运动(抛物线随顶点一起平移),
与轴交于,两点(点在点的左侧),点 的横坐标
的最大值为3,则点 的横坐标的最小值为____.
提示:当顶点在点处时,点的横坐标最大,此时,
两点的水平距离为4.由抛物线的对称性可知,, 两点的水平距离也为
4,所以.当顶点在点处时,点的横坐标最小,所以点 的横坐
标的最小值为 .
【点击查看网络画板】
图2
3.(2025·广西柳州·模拟)如图2,在平面直角坐标系
中,二次函数的图象与轴交于,
两点,点的坐标为,与轴交于点 ,
点 为抛物线的顶点.
(1)求这个二次函数的解析式.
解:将,代入 ,得
解得
故这个二次函数的解析式为 .
图2
(2)求 的面积.
解:由(1)知, .
所以.
当时, ,解得,.所以.
所以 .
故 .
攻坚练
4.把二次函数的图象作关于 轴的对称变换,所
得图象的函数解析式为.若 ,
则 的最大值是( ).
A. B.0 C.2 D.6
提示:因为把二次函数的图象作关于 轴的对称变换,所得图象的函数解析式为 ,所以原二次函数图象的顶点坐标为 ,即原二次函数.所以, .由,得.又 ,所以,即.所以 的最大值是6.
【答案】D
图3
5.边长为1的正方形的顶点在 轴的正半轴上,
如图3,将正方形绕顶点顺时针旋转 得
到正方形,使点恰好落在函数
的图象上,则 的值为_ ____.
提示:连接,过点作轴于点 .由题意,得 .因为 ,所以 .因为 ,所以
.所以, .所以,.将,代入 中,得.解得 .
图4
6.(2023·四川巴中·中考)如图4,在平面直角坐标系中,
抛物线经过点和点 ,
其顶点的横坐标为1.
(1)求抛物线对应的函数解析式.
解: 抛物线的顶点的横坐标为1, 对称轴为直线 .
又 抛物线经过点, 抛物线与 轴的另一交点为
设抛物线的对应函数解析式为.
将 代入,解得
抛物线对应的函数解析式为 .
(2)若直线与轴交于点,在第一象限内与抛物线交于点 ,当取何值时, 有最大值?并求出最大值.
图4
解 直线与轴交于点,与抛物线交于点 ,
,
点在第一象限, ,,
.
, 当时,有最大值,最大值为 .
图4
(3)若为抛物线 的对称轴上的
一个动点,将抛物线向左平移1个单位长度后, 为平移
后抛物线上的一个动点.在(2)的条件下求得的点 ,
是否能与点,, 构成平行四边形?若能构成,则请求
出点 的坐标;若不能构成,则请说明理由.
图12
解: , 向左平移1个单位长度后的抛物线对应的函数解析式为.
如图12,由(2)知,已知 ,设,
设存在以,,, 为顶点的平行四边形.
①当以为对角线时, 平行四边形的对角线互相平分,
.
解得
点 在抛物线上, .
点的坐标为
②当以为对角线时,同理可得, .
解得. . 点的坐标为
③当以 为对角线时,同理可得.
解得. .
点的坐标为.
综上所述,存在以,,, 为顶点的平行四边形,点的坐标为
或 或 .
图12
7.(2025·湖南衡阳·中考模拟)如图5,已知抛物线交 轴于
,两点,将该抛物线位于轴下方的部分沿 轴翻折,其余部分不变,
得到的新图象记为“图象”,图象交轴于点 .
图5
图5
(1)写出图象位于线段 上方部分对应的函数解析式.
解:当时,, .
当 时,,解得,
∴ , .
设图象位于线段 上方部分对应的函数解析式为,将 代入,得
∴ 图象 位于线段上方部分对应的函数解析式为
.
图5
(2)当直线与图象 有三个交点时,请结
合图象,直接写出 的值.
提示:由图象得,直线与图象 有三个交
点时,存在两种情况:①当直线过点
时,与图象有三个交点,此时 ;②当直线
与图象位于线段 上方部分相切时,
【答案】 的值是2或3.
图13
与图象有三个交点,如图13,由 ,得 .由,得 .综上所述, 的值是2或3.
(3)为轴正半轴上的一个动点,过点作轴交直线于点 ,
交图象于点.是否存在这样的点,使与 相似?若存在,
则求出所有符合条件的点 的坐标;若不存在,请说明理由.
图5
解:存在满足条件的点
, , 是等腰直角三角形.
①如图14,当,且点在点 左侧时,,此时点与点关于对称轴直线对称, 点的横坐标为
.
图14
图15
②如图15,当,且点 在点右侧时,,此时点的纵坐标为2.由 ,
解得,(舍去)
点的横坐标为.
如图16,当 时, ,此时直线的函数解析式为,联立方程组 解得,(舍去)
点的横坐标为.
.
综上所述,点的坐标为或 或.
图16
8.(2023·湖南益阳·中考)在平面直角坐标系中,直线
与轴交于点,与抛物线交于, 两点(点在点 的左边).
(1)求点 的坐标.
解:令,得, 点的坐标为 .
(2)如图6,若点关于轴的对称点为,当以,, 为顶点的三角形是直角三角形时,求实数 的值.
图6
解:联立直线与抛物线 的函数解析式,得
或
,
点关于 轴的对称点为,
图6
,
.
若 ,则,即, (负值已舍去).
若 ,则 ,即, (负值已舍去).
若 ,则 ,即
,此方程无解.
综上可知,或 .
图7
(3)定义:将平面直角坐标系中横坐标与纵坐标均
为整数的点叫作格点,如, 等均为格
点.如图7,直线与抛物线 所围成的封闭图形即阴
影部分(不包含边界)中的格点数恰好是26个,求
的取值范围.
图17
解:如图17, 直线与抛物线交于点, ,点的横坐标为,点的横坐标为2, 直线 与抛物线 所围成的封闭图形(不包含边界)中的格点只能落在轴和直线上.
,,,
格点数恰好是26个, 落在轴和直线 上的格点数应
各为13个.
点的纵坐标应满足,即 .
①若,即,则线段上的格点应该为, , ,, 点 的纵坐标应满足,即.
若,则,,则线段 上的格点
正好为13个.
综上所述,或 .
图17
靶向练
图8
9.(2024·广东深圳·中考节选)在综合实践课上,数学探
究小组用两个互相垂直的直尺制作了一个“ ”形尺,并用
它对二次函数图象的相关性质进行研究.把“ ”形尺按图8
的方式摆放,水平宽的中点为,图象的顶点为 ,测
得为时,为 .
(1)探究小组先对的图象进行多次测量,测得与 的部分
数据如下表:
0 2 3 4 5 6 …
0 1 2.25 4 6.25 9 …
描点:以表中各组对应值为点的坐标,在图9的平面直角坐标系内描出相应的点.
图8
【猜想】
图9
连线:用光滑的曲线顺次连接各点.
猜想:与 的函数解析式是_________.
解:描点连线绘制函数图象如图18.
图18
提示:由题意,得,.将点 的坐标代入
函数,得 .
【验证】
(2)探究小组又对多个二次函数的图象进行了测量研究,发现测得的
与 也存在类似的函数解析式,并针对二次函数
的情况进行了推理验证.请从下表中任选一种
方法(在“□”内画“√”)并补全其推理过程.(根据需要,选用字母 ,
,,, 表示答案)
□方法1 □方法2
,
,
图10
图11
□方法1 □方法2
图10
图11
续表
同课章节目录
