2026年中考《数学》复习课件 专题四 三角形--第17讲 线与角(共69张PPT)

(共69张PPT)
复习讲义
第一篇 考点精讲
专题四 三角形
图1
1.（2023·广西·中考第7题）如图1，一条公路两次
转弯后又回到与原来相同的方向，如果
，那么 的度数是( ).
D
A. B. C. D.
图2
2.（2024·广西·中考第6题）如图2，2时整，钟表的时针和分
针所成的锐角为( ).
C
A. B. C. D.
3.（2024·广西·中考第13题）已知与为对顶角， ，则
____ .
35
图3
4.（2023·广西·中考第17题）如图3，焊接一个
钢架，包括底角为 的等腰三角形外框和
高的支柱，共需钢材约____ （结果取整数；参
考数据：， ，
）.
21
【解析】由等腰三角形“三线合一”的性质，得.在 中，
， ，故共需钢材约
.
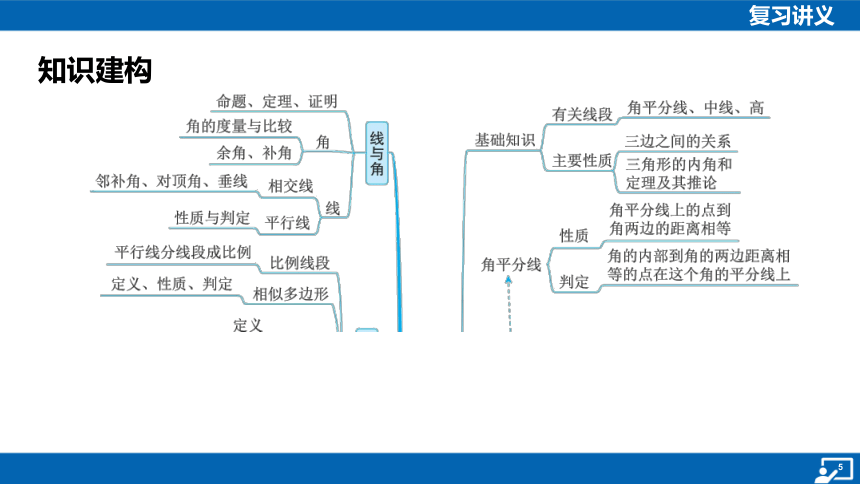
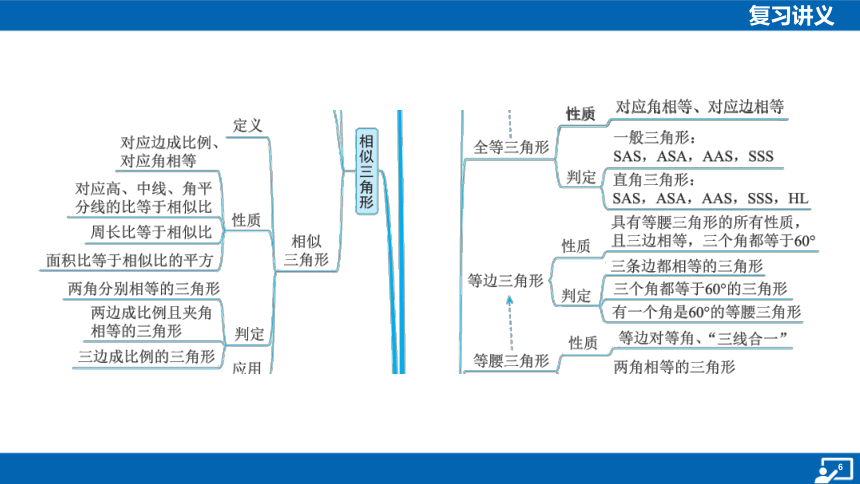
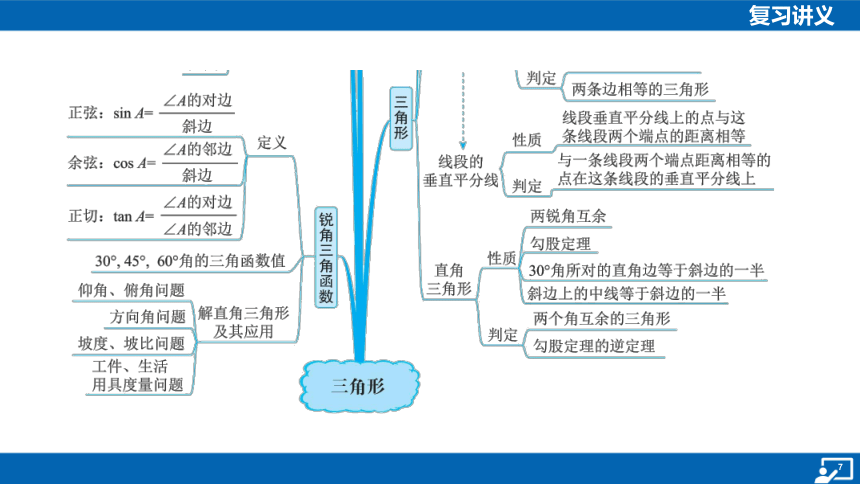
知识建构
第17讲 线与角
聚焦核心
1.直线、线段的有关概念和性质
（1）直线的性质：两点确定____条直线.
（2）线段的性质：两点之间，线段______.
（3）距离：连接两点间的线段的______.
（4）中点：把一条线段分成两条______的线段的点.
一
最短
长度
相等
2.角的有关概念和性质
（1）1周角_____ ，1平角_____ ，1直角____ ；
____，____ .
360
180
90
60
60
（2）余角、补角：
余角 定义 两个角的和等于____，就说这两个角互为余角
性质 同角（等角）的余角______
补角 定义 两个角的和等于______，就说这两个角互为补角
性质 同角（等角）的补角______
相等
相等
3.相交线的有关概念和性质
（1）对顶角的性质：对顶角______.
（2）邻补角的性质：邻补角______.
（3）垂线的性质：
①在同一平面内，过一点有且只有____条直线与已知直线垂直.
②连接直线外一点与直线上各点的所有线段中，________最短.简单说
成________最短.
（4）点到直线的距离：连接直线外一点到这条直线的垂线段的______.
相等
互补
一
垂线段
垂线段
长度
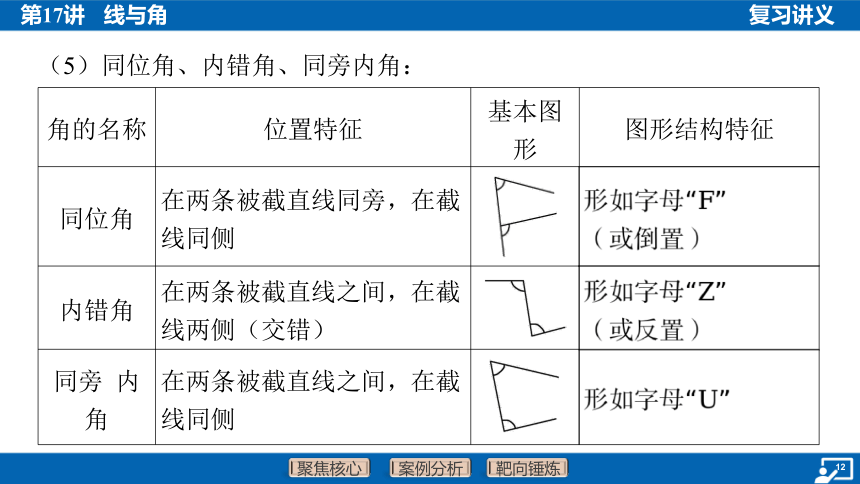
（5）同位角、内错角、同旁内角：
角的名称 位置特征 基本图 形 图形结构特征
同位角 在两条被截直线同旁，在截 线同侧 ___________________
内错角 在两条被截直线之间，在截 线两侧（交错） _______________________
同旁 内 角 在两条被截直线之间，在截 线同侧 ______________________
4.平行线
（1）平行公理：经过直线外一点，有且只有____条直线与已知直线平行.
推论：如果，，那么___ .
一
//
（2）平行线的性质与判定：
①两直线平行 同位角______；
②两直线平行 内错角______；
③两直线平行 同旁内角______.
相等
相等
互补
5.命题
（1）每个命题由______和______两部分组成.
（2）命题分为____命题和假命题.
条件
结论
真
（3）两个命题中，如果第一个命题的条件是第二个命题的结论，而第
一个命题的结论又是第二个命题的条件，那么这两个命题叫作互逆命题.
其中一个命题称为另一个命题的________.
逆命题
第17讲 线与角
案例分析
考点一 直线、射线、线段
名师指导
1.若点是线段的中点，则，.
2.（1）两点确定一条直线；
（2）两点之间，线段最短.
3.若一条直线上有个点，则以这些点为端点的线段有条.
（2）若恰好是的中点，则___ .
例1 一题多问 如图1，已知线段，为线段 上的一个动
点，是的中点，是 的中点.
图1
（1）图中共有____条线段.
10
提示：因为，恰好是 的中点，所以.因为，分别是和 的中点，所以， 所以 .
6
思路点拨（1）直线上有，，，，共5个点，则共有 条线段.
思路点拨 （2）根据线段的和差关系： 求解，因此需要利用线段的中点的定义求出， 的长.
（3）若，求 的长.
图1
解：因为，，所以 .
，分别是和的中点，所以 ，
以 .
思维点拨（3）同（2）中思路，利用线段的和差关系与线段的中点的定义求解.
（4）求证：无论取何值（小于）， 的长不变.
图1
证明：设，则 .
因为，分别是和的中点，所以 ， .
所以.
所以无论 取何值（小于），的长不变，为 .
思维点拨（4）同（2）中思路，利用线段的和差关系与线段的中点的定义求解.
考点专练
1.如图2，点，在线段 上，则下列表述或结论错误的是( ).
图2
D
A.若，则 B.
C. D.图中共有线段12条
考点二 角的有关概念及计算
名师指导
1. 与 互余； 与
互补.
2.角的度、分、秒换算是60进制.进行角的单位换算时，注意分步进
行.将大的单位化为小的单位，用乘法；将小的单位化为大的单位，用
除法.如：， .
3.进行角的加减运算时，要将度、分、秒分别相加减，分、秒相加
时逢60要进位，不够减时要向前一位借1作60.如：
， .
图3
例2（1）（2024·北京·中考）如图3，直线和 相
交于点，.若 ，则 的大
小为( ).
B
A. B. C.45 D.
思路点拨
（1）
（2）先将它们统一为只用度表示或统一为用度、分、秒表示，再
比较大小.
（2）下列各式正确的是( ).
D
A. B. C. D.
思路点拨
考点专练
2.如图4，7时30分时，时钟上的时针与分针的夹角为( ).
B
图4
A. B. C. D.
3.（2025·广西百色·中考模拟）已知 ，则它的余角为( ).
B
A. B. C. D.
4.（2024·江苏连云港·中考）已知的补角为 ，则_____ .
120
考点三 相交线
名师指导 在求相交线中的角的度数时，明确各角的位置关系是解题的
关键，由角的位置关系可得到它们的数量关系，由此可探究各角的度数.
常用到的知识点有：（1）已知条件中若有两直线垂直，则可知有四个
角是直角；（2）互为邻补角的两个角的和为 ；（3）对顶角相等；
（4）已知条件中若有角平分线，则可得到相等的两个角.
图5
例3 （2024·四川雅安·中考）如图5，直线， 交
于点，于点，若 ，则 的度数
是( ).
A. B. C. D.
提示：由， ，得 .由
对顶角的性质，得 .
A
思路点拨 （对顶角相等）
↑
与 互余
↑
考点专练
5.（2025·青海·中考模拟）数学课上老师用双手形象地表示了“三线八角”图
形，如图6所示（两大拇指代表被截直线，食指代表截线）．从左至右
依次表示( ).
图6
D
A.同旁内角、同位角、内错角 B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角 D.同位角、内错角、同旁内角
6.（2025·江苏常州·中考模拟）如图7，斑马线的作用是为了引导行人安全地
通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一
想法体现的数学依据是( ).
A
图7
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
考点四 平行线的性质与判定
名师指导
1.正确识别同位角、内错角、同旁内角是判定两直线平行的关键,只有同位角相等或内错角相等或同旁内角互补，才能得出两直线平行.
2.由两直线平行可得到两角相等或两角互补,因此已知两直线平行求角的度数问题,常寻找或构造同位角、内错角或同旁内角求解.
图8
例4 （2025·湖北武汉·中考）如图8，在四边形
中，， .
（1）求 的度数.
解：，.
， .
思路点拨（1）（要求的角）与 （已知角）是
直线，被直线 所截形成的同旁内角，且，则由平行线的性质可求得 的度数.
图8
（2）平分交于点， .求证：
.
证明：（方法一） 平分， ， .
∵ ， .
思维点拨（2）思路一：（已知角）与 是直
线，被直线 所截形成的同旁内角，要证
，则证 即可.思路二：
（已知角）与是直线，被直线所截形成的同位角，要证 ，则证 即可.
图8
， . .
（方法二） 平分， ， .
， .
， .
考点专练
图9
7.（2024·江苏盐城·中考）如图9，小明将一块
直角三角尺摆放在直尺上，若 ，则
的度数为( ).
B
A. B. C. D.
图10
8.跨学科题（2025·四川南充·中考模拟）如图10，两个
平面镜平行放置，光线经过平面镜反射时，
，则 的度数为( ).
C
A. B. C. D.
图11
9.（2024·江苏南通·中考）如图11，点在 的
边上，经过边的中点，且 .求
证： .
证明：是的中点，.
在 和中，，， ，
∴ .
考点五 关于线段、垂线段的最值问题
名师指导
1.在解决生活中的最短距离问题时，其理论依据通常是“两点之间，线段最短”或“垂线段最短”.“两点之间，线段最短”体现的是点与点的关系，“垂线段最短”体现的是点与直线的关系.
2.在数学问题中，“两点之间，线段最短”“垂线段最短”常结合三角形、四边形等几何知识进行考查，一般会涉及动点问题.解决这类问题的关键是“动中取静”，运用“两点之间，线段最短”或“垂线段最短”让动点定下来，再运用三角形、四边形的性质、定理解题.
图12
例5（1）（2025·广西柳州·中考模拟）如图12，
从学校到书店 有①，②，③，④四条路
线，其中最短的路线是( ).
B
A.① B.② C.③ D.④
思路点拨（1）两点的所有连线中，可以有无数种连法，如折线、曲线、线段等，这些线中线段最短．
图13
（2）（2025·四川雅安·中考模拟）如图13，在 中，
，，为边 上的一个动点，作
于点，于点，则 长的最小值为
_____．
思路点拨 （2）是四边形 的对角线，由图中线段之间的垂直关系，可判定四边形是矩形.结合矩形对角线相等的性质，可将求 的最小值转化为求的最小值.而是边上的动点，是定点，可看作点 与直线的关系，由“垂线段最短”可确定的长取最小值时点 的位置.
图13
提示：连接.由勾股定理，得 .
由，， ，得四边形 是矩形.由此可
得.由垂线段最短可知，当时， 的值最小.由等腰三
角形的性质，可知此时为的中点，则.故 的最小
值为 .
考点专练
图14
10.图14是两个生活中的现象，对于这两个
现象的解释，正确的是( ).
D
A.均用两点之间线段最短来解释
B.均用经过两点有且只有一条直线来解释
C.现象1用两点之间线段最短来解释，现象2用经过两点有且只有一条直线来解释
D.现象1用经过两点有且只有一条直线来解释，现象2用两点之间线段最短来解释
11.如图15，在中， ，，， ，
点是边上的动点，则线段 的最小值是____.
9.6
图15
图16
12.综合与实践
【问题情境】噪声产生的影响与距离有关，距离越
近，受噪声影响越严重.如图16，一辆汽车在笔直
的公路上由点向点行驶，点， 分别表示位于
公路 两侧的两个小区.
【提出问题】
图16
（1）请在图中画出汽车行驶到哪个位置时，小区 受噪声影响最严重，
并说明理由.
图19
解：如图19，过点作，垂足为点 ，点
即为所求.
理由：根据垂线段最短可知，当汽车行驶到此处时，距离小区最近，所以此时小区 受噪声影响最严重.
图16
（2）请在图中画出汽车行驶到哪个位置时，小区
受噪声影响最严重，并说明理由.
图19
解：如图19，过点作，垂足为点 ，点 即为所求.
理由：根据垂线段最短可知，汽车行驶到此处时，距离小区最近，所以此时小区 受噪声影响最严重.
【问题拓展】
图16
（3）当汽车在路段的什么范围内行驶时，小区
受噪声影响越来越小，而小区 受噪声影响越来越大
图19
解：如图19,汽车从点行驶到点时，小区 受噪声影响越来越小，而小区 受噪声影响越来越大.
第17讲 线与角
靶向锤炼
靶向练
1.（2024·甘肃·中考改编）若 ，则 的余角为( ).
A
A. B. C. D.
图1
2.（2024·湖北·中考）如图1，一条公路的两侧铺设
了，两条平行管道，并有纵向管道 连通，
若 ，则 的度数是( ).
B
A. B. C. D.
图2
3.如图2，为方便群众，需要从新建的广场 处修一条人
行通道到小路，沿，， 均可，其中
，为了节约资金应将人行通道修在( ).
B
A.处 B.处 C. 处 D.不能确定
4.（2025·广西梧州·中考模拟）下列命题中，是假命题的为( ).
A
A.的绝对值是
B.对顶角相等
C.平行四边形是中心对称图形
D.如果直线，，那么直线
图3
5.（2023·河南·中考）如图3，直线，相交于点 ，
若 ， ，则 的度数为( ).
B
A. B. C. D.
6.（2024·甘肃兰州·中考）如图4，小明在地图上量得 ，由此判
断幸福大街与平安大街互相平行，他判断的依据是( ).
B
图4
A.同位角相等，两直线平行
B.内错角相等，两直线平行
C.同旁内角互补，两直线平行
D.对顶角相等
图5
7.（2024·吉林·中考）如图5，从长春站去往胜利公园，与其
他道路相比，走人民大街路程最近，其蕴含的数学道理是
____________________.
两点之间，线段最短
8.74_______ .
74.325
9.如图6，已知，，点为的中点，则线段 的
长为___ ．
图6
1
图7
10.（2024·广东广州·中考）如图7，直线分别与直线，
相交，，若 ，则 的度数为______.
图8
11.如图8，直线，相交于点， ，
，判断与 的位置关系，并说明理由.
解：.
理由：， .
.
又 ， ，即 .
.
12.如图9，一个由4条线段构成的“鱼”形图案，其中 ，
， ，找出图中的平行线，并说明理由.
图9
解：，.
理由： ， .
， ， .
.
攻坚练
图10
13.（2024·内蒙古包头·中考）如图10，直线 ，
点在直线上，射线交直线于点 ，则图中与
互补的角有( ).
C
A.1个 B.2个 C.3个 D.4个
图11
14.（2024·四川巴中·中考）如图11，直线 ，一块
含有 角的直角三角尺按如图11所示放置.若
，则 的度数为( ).
A. B. C. D.
提示：如图19， .所以 .由 ，
得 .
图19
A
15.跨学科题（2025·山西·中考改编）一个杯子静止在斜面上，其受力分
析如图12所示，重力的方向竖直向下，支持力 的方向与斜面垂直，
摩擦力的方向与斜面平行.若斜面的坡角 ，则摩擦力 与重力
方向的夹角 的度数为______.
图12
图13
16.（2025·宁夏·中考改编）小明与小亮要到科技
馆参观.小明家、小亮家和科技馆的方位如图13所
示，则科技馆位于小亮家__________方向.
南偏东
提示：如图20，作 ，则 .从而得 .由， ，得.所以 .故科技馆位于小亮家南偏东 方向.
图20
图14
17.如图14，中， ， ，
点是边上的动点，连接，，是 的
中点，是的中点，则 的最小值是_ __.
提示：因为，分别为， 的中点，所以.故当时， 有最小值，即有最小值.过点作于点 .由平行四边形的性质，得 .在中， .由此可知，的最小值为，故的最小值为 .
图15
18.如图15，在中，，分别是， 上
的点，，是上的点，连接，， ，
， ．
（1）求证： .
证明： ， .
又 ，
.
（2）当是的平分线， 时，求 的度数．
图15
解： 是的平分线，且，
， ， .
∴ .
.
拔尖练
19.跨学科题 综合与实践
实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反
射出的光线与平面镜所夹的锐角相等.如图16，一束光线射到平面镜
上，被反射后的光线为，则入射光线、反射光线与平面镜 所夹的
锐角 .
图16
图17
（1）利用这个规律人们制作了潜望镜，图17是潜望镜的
工作原理示意图，， 是平行放置的两面平面镜.已
知光线经过平面镜反射时，有， ，请解
释进入潜望镜的光线为什么和离开潜望镜的光线 是平
行的.（请把证明过程补充完整）
证明： ，（已知）
.( )
两直线平行，内错角相等
图17
， ，（已知）
.( )
，即 .
.( )
等量代换
内错角相等，两直线平行
图18
（2）显然，改变两面平面镜， 之间的位置关
系，经过两次反射后，入射光线与反射光线 之间
的位置关系会随之改变.如图18，平面镜， 的
一端连接（点，重合），一束光线 射到平面镜
上，被反射到平面镜上，又被 反射.若
被反射出的光线与光线平行，且 ，
则____ ，____ .
图18
提示： ，
.
， . .
. .
.
图18
（2）显然，改变两面平面镜， 之间的位置关
系，经过两次反射后，入射光线与反射光线 之间
的位置关系会随之改变.如图18，平面镜， 的
一端连接（点，重合），一束光线 射到平面镜
上，被反射到平面镜上，又被 反射.若
被反射出的光线与光线平行，且 ，
则____ ，____ .
96
90
图16
（3）猜想：图18中，当两平面镜， 的夹角
____ 时，可以使任意入射光线 经过平面
镜，的两次反射后，反射光线与入射光线
平行.请证明上述猜想.
90
证明： ， .
，， .
.
.