2026年中考《数学》复习课件 专题四 三角形--微专题(七) 与角平分线有关的四种基本模型(共24张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件 专题四 三角形--微专题(七) 与角平分线有关的四种基本模型(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
复习讲义
第一篇 考点精讲
专题四 三角形
微专题(七) 与角平分线有关的四种基本模型
模型一 角平分线+边的垂线 双垂直
模型剖析
如图1,
图1
结论:, .
模型应用
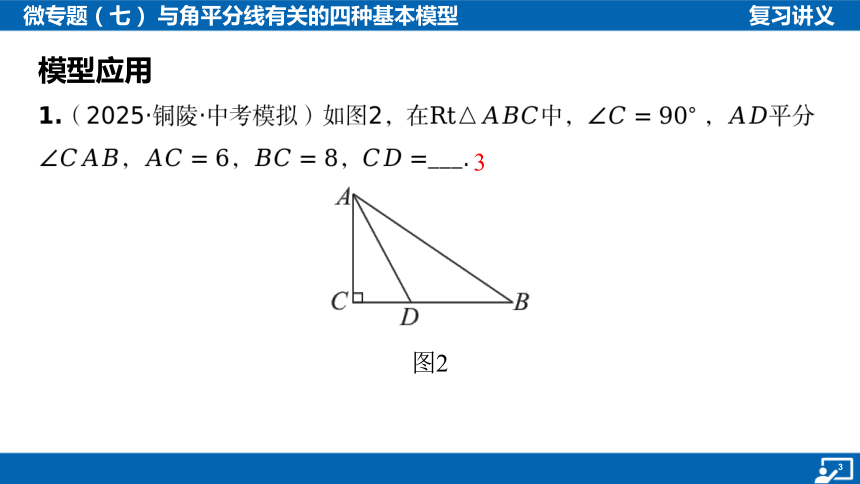
1.(2025·铜陵·中考模拟)如图2,在中, , 平分
,,, ___.
3
图2
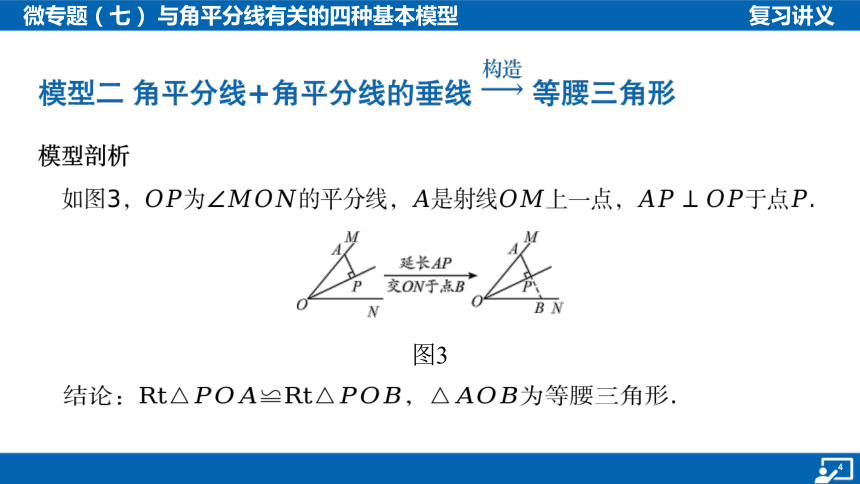
模型二 角平分线+角平分线的垂线 等腰三角形
模型剖析
如图3,
图3
结论:, 为等腰三角形.
模型应用
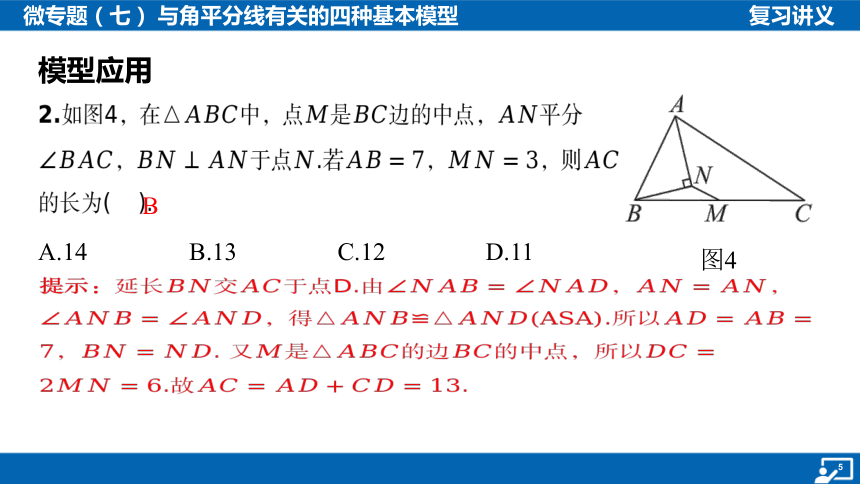
图4
2.如图4,在中,点是边的中点, 平分
,于点.若,,则
的长为( ).
A.14 B.13 C.12 D.11
提示:延长交于点D.由 ,, ,得.所以, . 又是的边的中点,所以 .故 .
B
模型三 角平分线+平行线 等腰三角形
模型剖析
如图5,
图5
结论: 为等腰三角形.
模型应用
图6
3.(2025·内蒙古鄂尔多斯·中考模拟)如图6,
,平分,交 于点
,,垂足为点.若,则 的长为
( ).
A.2 B. C.4 D.
提示:由,得.又 平分
,即,所以 .从
而得, .
过点作于点,则 .所以
.故 .
【答案】C
图6
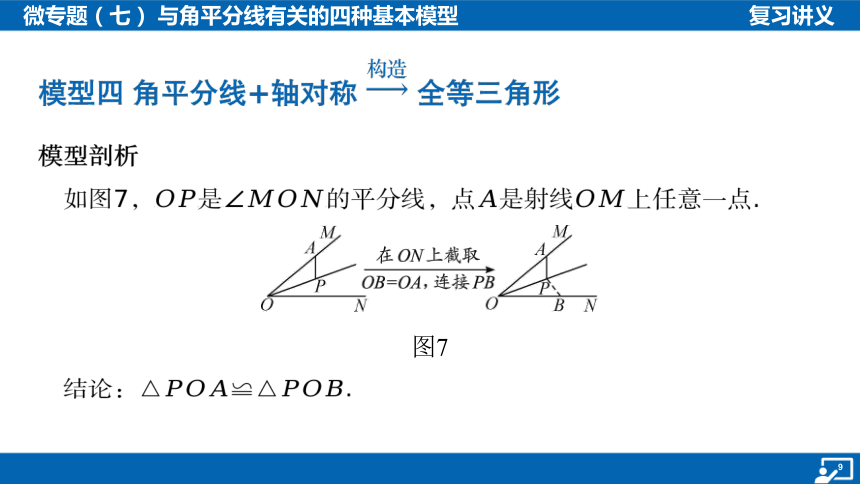
模型四 角平分线+轴对称 全等三角形
模型剖析
如图7,
图7
结论: .
模型应用
图8
4.如图8,在中,,平分 ,
交于点,,,则 ___.
3
提示:在边上取点,使,连接 .
由,, ,得
.所以 ,
.因为,,所以 .
从而得.故
微专题练习(七) 与角平分线有关的四种基本模型
模型一 角平分线+边的垂线 双垂直
图1
1.如图1,,的平分线与 的平分
线相交于点,作于点, ,则两
条平行线与 间的距离为( ).
D
A.5 B.8 C.9 D.10
2.如图2,为的平分线上一点,于点 ,
.
图2
求证: .
证明:过点作于点
.
为的平分线上一点,, , ,即 .
在R和中,,,
图2
, , .
在和中,,,,
= ,即 .
模型二 角平分线+角平分线的垂线 等腰三角形
图3
3.如图3,在中,是 的平分线,
,垂足为点.若 , ,则
____ .
50
提示:延长交于点,易得 是等腰三角
形,且.又 ,所以
.
4.如图4,在中, ,平分,交 的延长线于点,连接.已知,,求 的面积.
图4
图36
解:(方法一)如图36,延长 交的延长线于点
平分,
, .
在和中,,,,
,
,,
,
, .
图36
(方法二) ,平分,∴ .
,, .过点作于点 ,则
.
图36
模型三 角平分线+平行线 等腰三角形
5.如图5,在中,,平分,平分,
与交于点,,,则的周长是___ .
8
图5
6.如图6,在中, ,,, 和的平分线相交于点,过点作交于点,求 的长.
图6
解:如图37,过点作,交于点 ,则
平分,
.
同理可得
,, ,
图37
图37
, ,,
.
设,则,
, .
解得.
.
模型四 角平分线+轴对称 全等三角形
7.如图7,在四边形中,平分, ,
.求证:点在线段 的垂直平分线上.
图7
证明:如图38,在上截取 ,连接
平分, .
在和中, ,,,
,
图38
图38
, ,
∴
点在线段 的垂直平分线上.
8.如图8,在中, ,,是 的两条角平分线,,相交于点.求证: .
图8
证明:如图39,在边上取点,使得 ,连接
,,是 的角平分线, .
.
图39
图39
在和 中,,,,
.
.
在 和中,,,,
, .
复习讲义
第一篇 考点精讲
专题四 三角形
微专题(七) 与角平分线有关的四种基本模型
模型一 角平分线+边的垂线 双垂直
模型剖析
如图1,
图1
结论:, .
模型应用
1.(2025·铜陵·中考模拟)如图2,在中, , 平分
,,, ___.
3
图2
模型二 角平分线+角平分线的垂线 等腰三角形
模型剖析
如图3,
图3
结论:, 为等腰三角形.
模型应用
图4
2.如图4,在中,点是边的中点, 平分
,于点.若,,则
的长为( ).
A.14 B.13 C.12 D.11
提示:延长交于点D.由 ,, ,得.所以, . 又是的边的中点,所以 .故 .
B
模型三 角平分线+平行线 等腰三角形
模型剖析
如图5,
图5
结论: 为等腰三角形.
模型应用
图6
3.(2025·内蒙古鄂尔多斯·中考模拟)如图6,
,平分,交 于点
,,垂足为点.若,则 的长为
( ).
A.2 B. C.4 D.
提示:由,得.又 平分
,即,所以 .从
而得, .
过点作于点,则 .所以
.故 .
【答案】C
图6
模型四 角平分线+轴对称 全等三角形
模型剖析
如图7,
图7
结论: .
模型应用
图8
4.如图8,在中,,平分 ,
交于点,,,则 ___.
3
提示:在边上取点,使,连接 .
由,, ,得
.所以 ,
.因为,,所以 .
从而得.故
微专题练习(七) 与角平分线有关的四种基本模型
模型一 角平分线+边的垂线 双垂直
图1
1.如图1,,的平分线与 的平分
线相交于点,作于点, ,则两
条平行线与 间的距离为( ).
D
A.5 B.8 C.9 D.10
2.如图2,为的平分线上一点,于点 ,
.
图2
求证: .
证明:过点作于点
.
为的平分线上一点,, , ,即 .
在R和中,,,
图2
, , .
在和中,,,,
= ,即 .
模型二 角平分线+角平分线的垂线 等腰三角形
图3
3.如图3,在中,是 的平分线,
,垂足为点.若 , ,则
____ .
50
提示:延长交于点,易得 是等腰三角
形,且.又 ,所以
.
4.如图4,在中, ,平分,交 的延长线于点,连接.已知,,求 的面积.
图4
图36
解:(方法一)如图36,延长 交的延长线于点
平分,
, .
在和中,,,,
,
,,
,
, .
图36
(方法二) ,平分,∴ .
,, .过点作于点 ,则
.
图36
模型三 角平分线+平行线 等腰三角形
5.如图5,在中,,平分,平分,
与交于点,,,则的周长是___ .
8
图5
6.如图6,在中, ,,, 和的平分线相交于点,过点作交于点,求 的长.
图6
解:如图37,过点作,交于点 ,则
平分,
.
同理可得
,, ,
图37
图37
, ,,
.
设,则,
, .
解得.
.
模型四 角平分线+轴对称 全等三角形
7.如图7,在四边形中,平分, ,
.求证:点在线段 的垂直平分线上.
图7
证明:如图38,在上截取 ,连接
平分, .
在和中, ,,,
,
图38
图38
, ,
∴
点在线段 的垂直平分线上.
8.如图8,在中, ,,是 的两条角平分线,,相交于点.求证: .
图8
证明:如图39,在边上取点,使得 ,连接
,,是 的角平分线, .
.
图39
图39
在和 中,,,,
.
.
在 和中,,,,
, .
同课章节目录
