2026年中考数学复习课件 专题六 圆--第28讲 与圆有关的综合题(共81张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题六 圆--第28讲 与圆有关的综合题(共81张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 14:28:19 | ||
图片预览






文档简介
(共81张PPT)
复习讲义
第一篇 考点精讲
专题六 圆
第28讲 与圆有关的综合题
聚焦核心
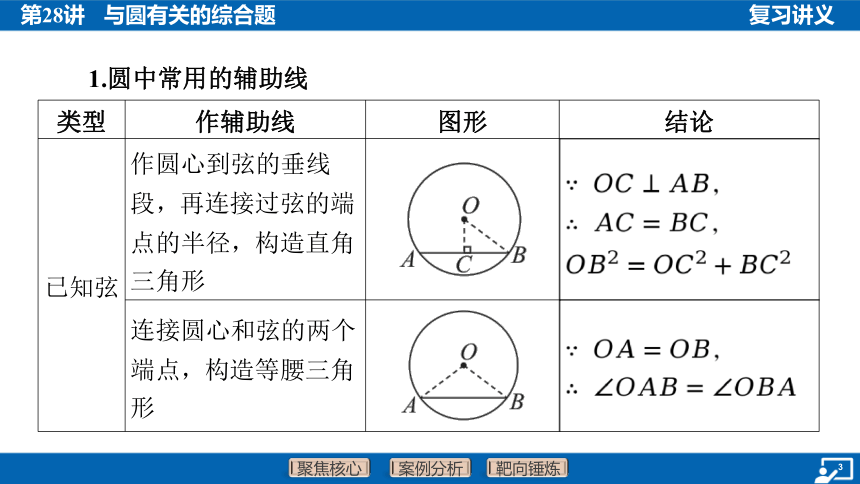
1.圆中常用的辅助线
类型 作辅助线 图形 结论
已知弦 作圆心到弦的垂线 段,再连接过弦的端 点的半径,构造直角 三角形 ___________________________________ ,
,
连接圆心和弦的两个 端点,构造等腰三角 形 __________________________________ ,
类型 作辅助线 图形 结论
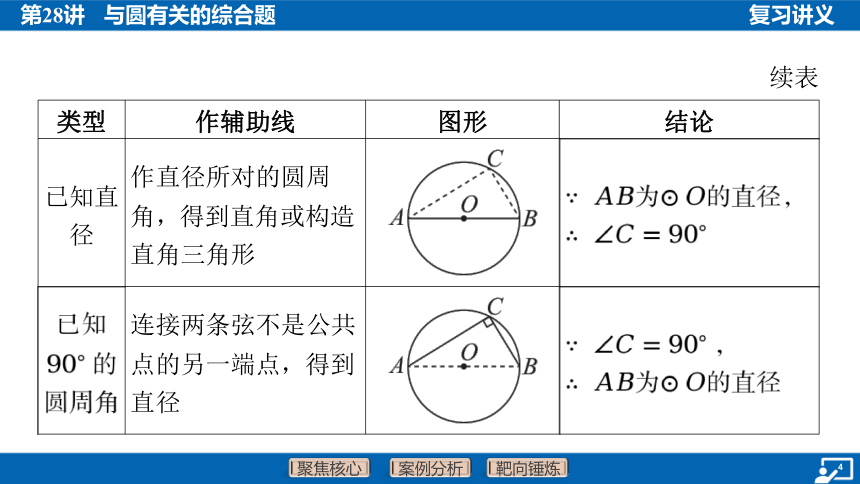
已知直 径 作直径所对的圆周 角,得到直角或构造 直角三角形 _________________________________________ 为 的直径,
已知 的 圆周角 连接两条弦不是公共 点的另一端点,得到 直径 _________________________________________ ,
为 的直径
续表
类型 作辅助线 图形 结论
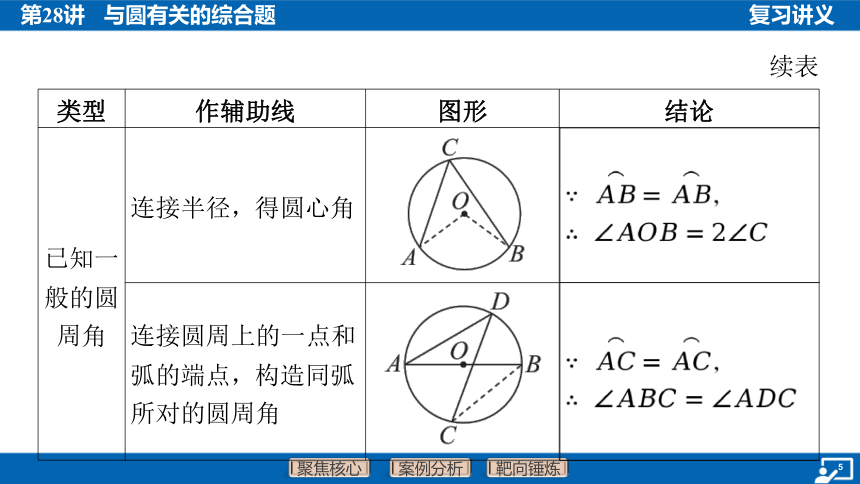
已知一 般的圆 周角 连接半径,得圆心角 __________________________________ ,
连接圆周上的一点和 弧的端点,构造同弧 所对的圆周角 __________________________________________ ,
续表
类型 作辅助线 图形 结论
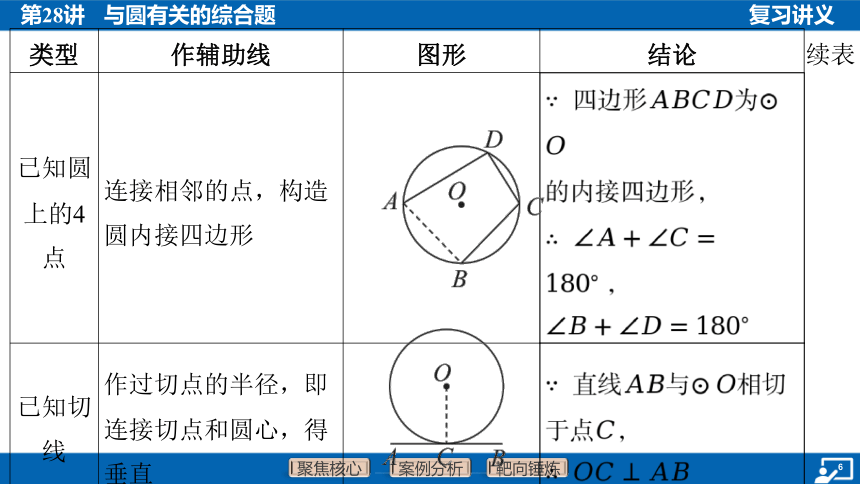
已知圆 上的4 点 连接相邻的点,构造 圆内接四边形 ____________________________________________ 四边形为
的内接四边形,
,
已知切 线 作过切点的半径,即 连接切点和圆心,得 垂直 __________________________________ 直线与 相切
于点 ,
续表
类型 作辅助线 图形 结论
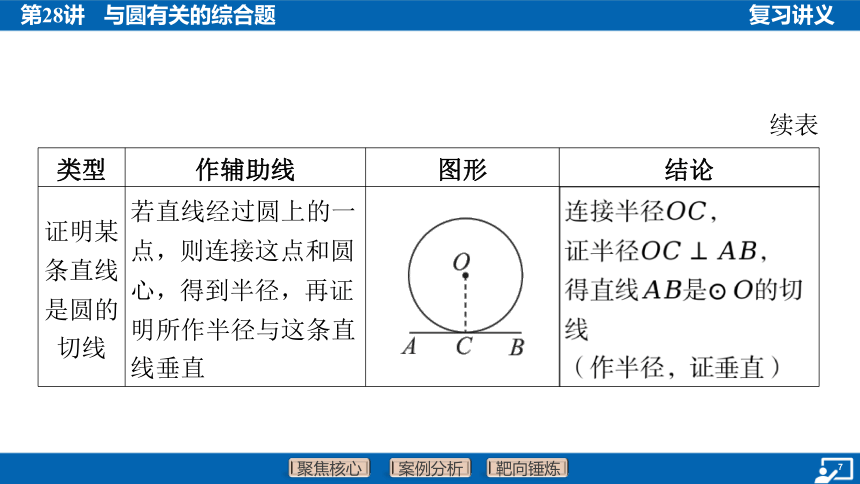
证明某 条直线 是圆的 切线 若直线经过圆上的一 点,则连接这点和圆 心,得到半径,再证 明所作半径与这条直 线垂直 __________________________________ 连接半径 ,
证半径 ,
得直线是 的切
线
(作半径,证垂直)
续表
类型 作辅助线 图形 结论
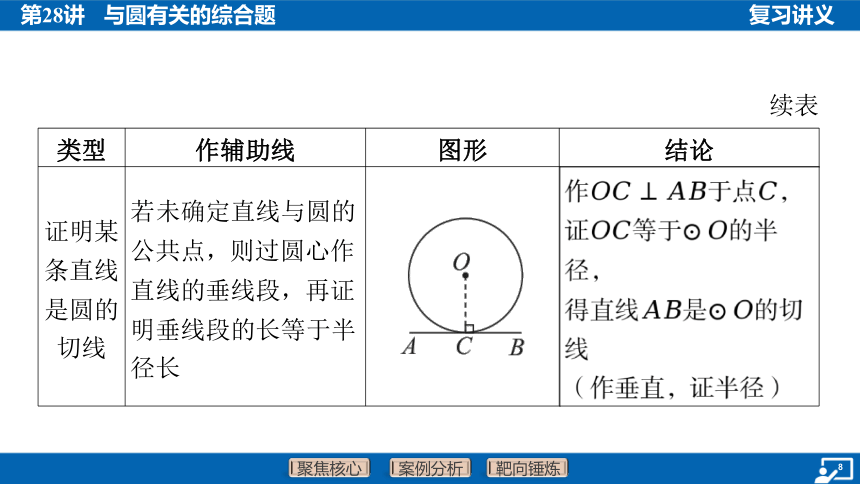
证明某 条直线 是圆的 切线 若未确定直线与圆的 公共点,则过圆心作 直线的垂线段,再证 明垂线段的长等于半 径长 __________________________________ 作于点 ,
证等于 的半
径,
得直线是 的切
线
(作垂直,证半径)
续表
2.圆中常用的基本模型
基本 模型 模型展示
角平 分线 模型 已知:如图1,是的直径,于点 ,
于点,与相切于点 .
【常见结论与方法】
(1)平分
(2),
(3),
连接,过点作于点,四边形 是矩形
图1
直角 三角 形模 型 已知:如图2,是的直径,,与 相切于点,交于点,与的延长线交于点 .
【常见结论与方法】
(1)
(2)
(3)连接,, ,
, ____________________________
图2
续表
弦切 角模 型 (切 割线 模 型) 已知:如图3,与相切于点,直线与 交于点
, . 【常见结论与方法】
(1)
(2) ,
(3),且是与 的相似比
(4)若已知,,,,, 中任意两个量,则可求出其余量________________________________
图3
续表
切线 长模 型 已知:如图4,,与分别相切于, 两点,连接
,, .
【常见结论与方法】
(1)
(2)平分
(3)
(4) _______________________________
图4
续表
第28讲 与圆有关的综合题
案例分析
考点一 圆与全等三角形问题
名师指导 当关于圆的题目中图形较复杂(如含三角形、四边形等),
需要求线段长或证明线段、角相等时,通常可证相关的两个三角形全等,
由全等三角形的性质得到相等的边和角,为解题提供条件.解题时,要
注意切线长定理的应用.
例1 (2024·湖北·中考)如图5,在中, ,点 在上,以为直径的经过上的点,与交于点 ,且 .
图5
(1)求证:是 的切线.
思路点拨(1)已知直线与 的公共点,则考虑“作半径,证垂直”,即连接,证明,
即可得到 ,根据切线的判定定理即可证得结论.
图5
图52
证明:如图52,连接.
在和中,, ,,
.
是的半径,是 的切线.
图5
(2)已知,,求 的长.
解:设的半径为.
在中, ,,,, .
解得
思思路点拨 (2)要求的长,关键是求出⊙ 的半径和的度数.设的半径为,在 中,由勾股定理可求得,和的度数,进而求得 的度数.
..
.
由(1)知,.
的长= .
图5
考点专练
图6
1.(2025·内蒙古通辽·中考改编)如图6,在 中,
,为边上一点,以点 为圆心,
的长为半径作圆与相切于点,连接 .
(1)求证: .
证明:如图59,连接
为的切线,
., .
, .
图59
图6
(2)当,时,求 的半径.
解:如图59,连接.
在 中,.
在和 中,,,
.
设的半径为,则, .
在R中,,解得
的半径长为3.
考点二 圆与相似三角形问题
名师指导 当要求线段的长、线段的比值,或要证明线段间的数量关系
时,通常可以利用圆的性质构造相似三角形解决.由于圆中很容易找到
直角或其他相等的角,因此对于圆中判定三角形相似的问题,通常用
“两角分别相等的两个三角形相似”来解决.运用相似三角形的对应边成比
例和圆的半径相等,可实现线段之间的等量代换,为解题提供条件.
图7
例2 (2024·陕西·中考)如图7,直线与 相切
于点,是的直径,点,在直线 上,且
位于点的两侧,连接,,分别与 交于
点,,连接,, .
(1)求证: .
思路点拨(1)由切线的性质及圆周角定理的推论,可得 ,再利用同角的余角相等即可证明 .
证明:直线与相切于点,.
.
是的直径,.
.
.
图7
(2)当的半径,,时,求 的长.
图7
思路点拨 (2)观察图形发现,分别在, 中,且这两个三角形有公共角,,, 可求,要求 的长,则考虑找到这两个三角形中的另一对角相等来证相似,然后由相似三角形的性质列式求 的长.
图7
又,
,即. .
解:,
直线 与相切于点,.
,,.
是 的直径,.
. ,.由(1)知,,∴ .
考点专练
图8
2.(2024·江苏无锡·中考)如图8,是 的直
径,内接于,,, 的延
长线相交于点,且 .
(1)求证: .
证明:,
,
.
又 .
(2)求 的度数.
图8
解:连接
为的直径,.
设 .
由(1)知,则
四边形是 的内接四边形,,即.
解得.
.
考点三 圆与锐角三角函数问题
名师指导 对于圆与锐角三角函数的问题,一般会综合相似三角形的性质
与判定、勾股定理、圆周角定理、切线的性质与判定等知识一起考查.当求
一个角的三角函数或已知一个角的三角函数值时,需要把这个角转化到直
角三角形中求解,故适当地添加辅助线构造直角三角形是解题的关键.
图9
例3 (2025·江苏扬州·中考模拟)如图9,在 中, ,是上一点,且, 在上,以点为圆心的圆经过, 两点.
(1)试判断直线与 的位置关系,并说明理由.
思路点拨(1)观察图形,猜想直线与 相切.
连接,已知是的半径,要证直线是
的切线,只要证明即可.由 ,
可知 ,因此需要证明 .
图53
解:直线与 相切.
理由如下:如图53,连接
,,
,.
.
.
是的半径,直线与 相切.
图9
(2)当,的半径为3时,求 的长.
解:在中,, ,
.
在 中,,设,则
.
思路点拨 (2),在中,且在 中,故可根据正弦的定义和勾股定理列方程求解.
考点专练
3.(2024·湖南·中考)
【问题背景】 已知点是半径为的上的定点,连接 ,将线
段绕点按逆时针方向旋转得到,连接 ,过点
作的切线,在直线上取点,使得 为锐角.
【初步感知】
(1)如图10,当 时,____ .
30
图10
提示:由题意,得.又, 是等边三角形..直线是的切线,.∴ .
【问题探究】
(2)以线段为对角线作矩形,使得边过点,连接 ,对
角线,相交于点 .
①如图11,当时,求证:无论 在给定的范围内如何变化,
总成立.
图11
证明:,
,∴ .
直线是的切线, .
.
图11
四边形 是矩形,,
.
.
在和中,,,,∴
四边形是矩形,
, .
②如图12,当,时,请补全图形,并求 及 的值.
图12
解:补全图形如图60.过点作于点 ,过点作于点,连接,在 中,,, ,
.
,
此时点在线段上.
图60
图60
,,,.
,.
.
在中,,设 ,则
.
在中, .
四边形是矩形,
. .
考点四 圆中有关几何图形面积的问题
名师指导 可运用转化思想求圆中几何图形的面积.如果所求面积的图形
是规则图形,那么可直接应用相关面积公式计算;如果所求面积的图形
不是规则图形,就要转化为规则图形求解.在圆中求规则图形的面积,
除了扇形,也会涉及求三角形的面积,可以利用圆中的各种垂直关系直
接用面积公式求解,也可以利用相似三角形的性质求解.
例4 (2025·江苏南通·中考改编)如图13,等腰三角形 的顶角 ,与底边相切于点,并与两腰, 分别相交于点,,连接, .
图13
(1)求证:四边形 是菱形.
思路点拨 (1)只要证明和 都是等边三角形,就可推出四边形 的四条边相等,从而证得结论.
证明:如图54,连接
与底边 相切于点,
,, .
又 ,,和都是等边三角形.
,
四边形 是菱形.
图54
(2)当 的半径为2时,求图中阴影部分的面积.
图13
图54
解:如图54,连接交于点
四边形 是菱形,, ,.
在中,, .
.
.
思路点拨 (2)根据图中阴影部分的面积扇形 的面积-菱形 的面积,进行计算即可.
考点专练
图14
4.(2024·四川内江·中考)如图14,是 的直径,
是的中点,过点作的垂线,垂足为点 .
(1)求证: .
证明:是的直径,.
, .
是的中点, .
.
(2)求证:是 的切线.
图14
证明:如图61,连接
,
,
,
是的半径,是 的切线.
图61
(3)已知, ,求阴影部分的面积.
图14
图61
解:如图61,连接,,与相交于点
是的直径,.
.
又 ,四边形是矩形.
∴
是的半径,是的中点, ,,即
,
.
.
∴ .
图61
考点五 与圆有关的综合实践题
名师指导 与圆有关的综合实践题,一般会涉及材料阅读或操作探究或
生活情境,在解这类题时,要仔细阅读题目,提取关键信息,或根据题
意动手操作,找到解题的关键点.这类题目一般阅读量较大、综合性较
强,需要运用多个知识点,在解此类题时,不要畏难,一个小问一个小
问地解决,通常小问之间会有所关联,可以类比迁移.
例5 (2024·江苏连云港·中考)
【问题情境】
(1)如图15,圆与大正方形的各边都相切,小正方形是圆的内接正方
形,那么大正方形面积是小正方形面积的几倍?小昕将小正方形绕圆心
旋转 (如图16),这时候就容易发现大正方形面积是小正方形面积
的___倍.由此可见,图形变化是解决问题的有效策略.
2
图15
图16
思路点拨(1)观察旋转后的图形,可发现大正方形面积-小正方形面积= 个直角三角形的面积,再结合勾股定理可得出两正方形的面积关系.
【操作实践】
(2)如图17,图①是一个对角线互相垂直的四边形,边,,, 之
间存在某种数量关系.小昕按图17所示步骤进行操作,并将最终图形抽
象成图18.请你结合整个变化过程,直接写出图18中以矩形内一点
为端点的四条线段之间的数量关系.
图17
图18
提示:如图55,设与交于点.因为 ,所以
,, ,
.所以 .结合图形变换,得
.
图55
解:
思路点拨 (2)图形变换前后,线段的长不变,类比第(1)题,结合勾股定理可得线段之间的数量关系.
【探究应用】
(3)如图19,在图17④的基础上,小昕将绕点 逆时针旋转,,他发现旋转过程中存在最大值.已知 ,,当最大时,求 的长.
图19
思路点拨 (3)由旋转可知,点在以点为圆心, 为半径的圆上运动.观察图形并想象当点沿运动时的大小变化,可知当与 相切时, 最大.再结合(2)的相关结论解题.
解:如图56,将绕点逆时针旋转,点在以点 为圆心,
为半径的圆上运动.
,为的一个定点.
当与 相切时,最大.
则此时
.
由(2)可知,
.
图56
(4)如图20,在中, ,点, 分别在边和上,连接,,.已知, ,求 的最小值.
图20
解:如图57,将沿对折,点的对应点为点,将 沿对折,点的对应点为点,连接,, .
图57
思路点拨 (4)可类比(2)中图形的变换,对图20进行一定变换,将 等量转换到同一直线上,则此时 的值最小.解题时,可运用前面小问的结论.
再将沿方向平移,使点与点重合,如图58,得 ,连接 .
结合图形变换,得.
当,, 三点共线时,的值最小,最小值为的长.
,, ,
.
∴的最小值为 .
图57
图58
考点专练
5.(2025·青海·中考模拟)综合与实践
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做
成圆形的呢?这里面有什么数学道理吗?带着这样的疑问,小青做了如
下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.
【探究一】
(1)将车轮设计成等边三角形,转动过程如图21,设其中心到顶点的
距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨
迹是,,圆心角 .此时中心轨迹最
高点是(即的中点),转动一次前后中心的连线是 (水平线).
请在图22中计算到的距离 .
图21
图22
解:如图62,连接
,为的中点, ,.
,是等边三角形.
∴
.
图62
【探究二】
(2)将车轮设计成正方形,转动过程如图23,设其中心到顶点的距离
是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是
,,圆心角 .此时中心轨迹最高点是
(即的中点),转动一次前后中心的连线是 (水平线).请在图
24中计算到的距离 .(结果保留根号)
图23
图24
解:,为的中点,, ,.
.
∴ .
图23
图24
【探究三】
(3)将车轮设计成正六边形,转动过程如图25(见下页),设其中心
到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,
中心的轨迹是,圆心角的度数是____.此时中心轨迹最高点是
(即的中点),转动一次前后中心的连线是 (水平线),在图26
中计算到的距离 _______.(结果保留根号)
图25
图26
【归纳推理】
(4)比较,, 大小:_____________.按此规律推理,车轮设计
成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线
(水平线)的距离______(填“越大”或“越小”).
越小
【得出结论】
(5)将车轮设计成圆形,转动过程如图27,其中心(即圆心)的轨迹
与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)
的距离 ___.这样车辆行驶平稳、没有颠簸感.因此,将车轮设计成圆
形最适合行驶.
0
图27
第28讲 与圆有关的综合题
靶向锤炼
靶向练
图1
1.(2024·山东济宁·中考节选)如图1, 内接于
,是上一点,是 外一点,
,,连接.当 时,
求 的长.
解: , ,即
.
在和中,, ,,
.
图2
2.教材变式[湘教版九下第68页例3变式](2024·江苏
盐城·中考)如图2,点在以为直径的 上,过点
作的切线,过点作,垂足为点 ,连接
, .
(1)求证: .
证明:连接
是的切线,
,
是的直径, .
∴
.
(2)已知,,求 的半径.
图2
解: ,, ,
, ,即.
.
的半径为 .
攻坚练
图3
3.(2024·甘肃兰州·中考)如图3, 内接于
,为的直径,点为 上一点,
,延长至点,使 .
(1)求证:是 的切线.
图76
证明:如图76,连接,则
为的直径, .
.
在R和中,,,
,
,即 ,
是 的半径, 是 的切线.
图3
(2)已知,,求 的长.
解: , .
由(1)知, .
由(1)知,又 ,
.
,
,即.
解得 (舍去)或.
.
4.(2025·山东烟台·中考模拟)如图4,在菱形中,对角线, 相交于点,经过,两点,交对角线于点,连接交于点 ,且 .
图4
(1)求证:是 的切线.
图77
证明:如图77,连接,则
, .
四边形是菱形,
.
∴ .又 是的半径, 是 的切线.
图4
(2)已知 的半径与菱形的边长之比为5∶8,求 的值.
解: ,, .
∴ .
设,则
∴
,
四边形是菱形, , .
∴
∴ .
5.(2024·宁夏·中考)如图5,是的外接圆,为直径,点 是的内心,连接并延长交于点,过点作 的切线交的延长线于点 .
图5
(1)求证: .
证明:如图78,连接,交于点
,
为 的内心,
图78
图78
为的直径, .
∴ .
为的切线且为 的半径, ,即 .
∴
.
图5
(2)连接,的半径为2, ,求阴影部分的面积.(结果用含 的式子表示)
图78
解:如图78,连接, , .
.
又 , .
∴ .
.
拔尖练
图6
6.(2024·山东潍坊·中考)
【问题提出】在绿化公园时,需要安装一定数量的自动喷
洒装置,定时喷水养护.某公司准备在一块边长为 的正
方形草坪(如图6)中安装自动喷洒装置,为了既节约安装
成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方
案.[说明:一个自动喷洒装置的喷洒范围是半径为 的圆面.喷洒覆
盖率,为待喷洒区域面积, 为待喷洒区域中的实际喷洒面积]
【数学建模】这个问题可以转化为用圆面覆盖正方形面积的数学问题.
图6
【探索发现】
图7
(1)如图7,在该草坪中心位置设计安装1个喷洒半径为
的自动喷洒装置,该方案的喷洒覆盖率______.
取
0.785
提示:当喷洒半径为 时,喷洒面积 ,正方形草坪的面积=.故喷洒覆盖率 .
(2)如图8,在该草坪内设计安装4个喷洒半径均为 的自动喷洒装置;
如图9,设计安装9个喷洒半径均为 的自动喷洒装置……此类推,如
图10,设计安装个喷洒半径均为 的自动喷洒装置.与(1)中的方
案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒
覆盖率?请判断并给出理由.
图8
图9
图10
解:对于任意的,喷洒面积 ,而草坪面积始终为.
因此,无论取何值,喷洒覆盖率始终为 .
这说明增加装置个数同时减小喷洒半径,对提高喷洒覆盖率不起作用.
图8
图9
图10
(3)如图11所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,
且使得该草坪的喷洒覆盖率.已知 ,设
,的面积为,求关于的函数解析式,并求当
取得最小值时 的值.
图11
图11
解:连接,要使喷洒覆盖率,即 ,其中为草坪面积,为喷洒面积.
, ,,都经过正方形的中心点
,,
, 为的直径,即.
在 中,由勾股定得,得
.
当 时,取得最小值,此时,解得 (负值已舍去).
【问题解决】
图6
(4)该公司现有喷洒半径为 的自动喷洒装置若干个,
至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率
?(直接写出结果即可)
提示:由(3)可得,当的面积最小时, 为边长
为的正方形的外接圆.当 时,圆的内接正方形
解:至少安装9个这样的喷洒装置可使该草坪的喷洒覆盖率 .
的边长为,而草坪的边长为, ,即将草
坪分为9个正方形,将半径为 的自动喷洒装置放置于
9个正方形的中心,此时所用装置个数最少.故至少安装9个
这样的喷洒装置可使该草坪的喷洒覆盖率 .
图6
复习讲义
第一篇 考点精讲
专题六 圆
第28讲 与圆有关的综合题
聚焦核心
1.圆中常用的辅助线
类型 作辅助线 图形 结论
已知弦 作圆心到弦的垂线 段,再连接过弦的端 点的半径,构造直角 三角形 ___________________________________ ,
,
连接圆心和弦的两个 端点,构造等腰三角 形 __________________________________ ,
类型 作辅助线 图形 结论
已知直 径 作直径所对的圆周 角,得到直角或构造 直角三角形 _________________________________________ 为 的直径,
已知 的 圆周角 连接两条弦不是公共 点的另一端点,得到 直径 _________________________________________ ,
为 的直径
续表
类型 作辅助线 图形 结论
已知一 般的圆 周角 连接半径,得圆心角 __________________________________ ,
连接圆周上的一点和 弧的端点,构造同弧 所对的圆周角 __________________________________________ ,
续表
类型 作辅助线 图形 结论
已知圆 上的4 点 连接相邻的点,构造 圆内接四边形 ____________________________________________ 四边形为
的内接四边形,
,
已知切 线 作过切点的半径,即 连接切点和圆心,得 垂直 __________________________________ 直线与 相切
于点 ,
续表
类型 作辅助线 图形 结论
证明某 条直线 是圆的 切线 若直线经过圆上的一 点,则连接这点和圆 心,得到半径,再证 明所作半径与这条直 线垂直 __________________________________ 连接半径 ,
证半径 ,
得直线是 的切
线
(作半径,证垂直)
续表
类型 作辅助线 图形 结论
证明某 条直线 是圆的 切线 若未确定直线与圆的 公共点,则过圆心作 直线的垂线段,再证 明垂线段的长等于半 径长 __________________________________ 作于点 ,
证等于 的半
径,
得直线是 的切
线
(作垂直,证半径)
续表
2.圆中常用的基本模型
基本 模型 模型展示
角平 分线 模型 已知:如图1,是的直径,于点 ,
于点,与相切于点 .
【常见结论与方法】
(1)平分
(2),
(3),
连接,过点作于点,四边形 是矩形
图1
直角 三角 形模 型 已知:如图2,是的直径,,与 相切于点,交于点,与的延长线交于点 .
【常见结论与方法】
(1)
(2)
(3)连接,, ,
, ____________________________
图2
续表
弦切 角模 型 (切 割线 模 型) 已知:如图3,与相切于点,直线与 交于点
, . 【常见结论与方法】
(1)
(2) ,
(3),且是与 的相似比
(4)若已知,,,,, 中任意两个量,则可求出其余量________________________________
图3
续表
切线 长模 型 已知:如图4,,与分别相切于, 两点,连接
,, .
【常见结论与方法】
(1)
(2)平分
(3)
(4) _______________________________
图4
续表
第28讲 与圆有关的综合题
案例分析
考点一 圆与全等三角形问题
名师指导 当关于圆的题目中图形较复杂(如含三角形、四边形等),
需要求线段长或证明线段、角相等时,通常可证相关的两个三角形全等,
由全等三角形的性质得到相等的边和角,为解题提供条件.解题时,要
注意切线长定理的应用.
例1 (2024·湖北·中考)如图5,在中, ,点 在上,以为直径的经过上的点,与交于点 ,且 .
图5
(1)求证:是 的切线.
思路点拨(1)已知直线与 的公共点,则考虑“作半径,证垂直”,即连接,证明,
即可得到 ,根据切线的判定定理即可证得结论.
图5
图52
证明:如图52,连接.
在和中,, ,,
.
是的半径,是 的切线.
图5
(2)已知,,求 的长.
解:设的半径为.
在中, ,,,, .
解得
思思路点拨 (2)要求的长,关键是求出⊙ 的半径和的度数.设的半径为,在 中,由勾股定理可求得,和的度数,进而求得 的度数.
..
.
由(1)知,.
的长= .
图5
考点专练
图6
1.(2025·内蒙古通辽·中考改编)如图6,在 中,
,为边上一点,以点 为圆心,
的长为半径作圆与相切于点,连接 .
(1)求证: .
证明:如图59,连接
为的切线,
., .
, .
图59
图6
(2)当,时,求 的半径.
解:如图59,连接.
在 中,.
在和 中,,,
.
设的半径为,则, .
在R中,,解得
的半径长为3.
考点二 圆与相似三角形问题
名师指导 当要求线段的长、线段的比值,或要证明线段间的数量关系
时,通常可以利用圆的性质构造相似三角形解决.由于圆中很容易找到
直角或其他相等的角,因此对于圆中判定三角形相似的问题,通常用
“两角分别相等的两个三角形相似”来解决.运用相似三角形的对应边成比
例和圆的半径相等,可实现线段之间的等量代换,为解题提供条件.
图7
例2 (2024·陕西·中考)如图7,直线与 相切
于点,是的直径,点,在直线 上,且
位于点的两侧,连接,,分别与 交于
点,,连接,, .
(1)求证: .
思路点拨(1)由切线的性质及圆周角定理的推论,可得 ,再利用同角的余角相等即可证明 .
证明:直线与相切于点,.
.
是的直径,.
.
.
图7
(2)当的半径,,时,求 的长.
图7
思路点拨 (2)观察图形发现,分别在, 中,且这两个三角形有公共角,,, 可求,要求 的长,则考虑找到这两个三角形中的另一对角相等来证相似,然后由相似三角形的性质列式求 的长.
图7
又,
,即. .
解:,
直线 与相切于点,.
,,.
是 的直径,.
. ,.由(1)知,,∴ .
考点专练
图8
2.(2024·江苏无锡·中考)如图8,是 的直
径,内接于,,, 的延
长线相交于点,且 .
(1)求证: .
证明:,
,
.
又 .
(2)求 的度数.
图8
解:连接
为的直径,.
设 .
由(1)知,则
四边形是 的内接四边形,,即.
解得.
.
考点三 圆与锐角三角函数问题
名师指导 对于圆与锐角三角函数的问题,一般会综合相似三角形的性质
与判定、勾股定理、圆周角定理、切线的性质与判定等知识一起考查.当求
一个角的三角函数或已知一个角的三角函数值时,需要把这个角转化到直
角三角形中求解,故适当地添加辅助线构造直角三角形是解题的关键.
图9
例3 (2025·江苏扬州·中考模拟)如图9,在 中, ,是上一点,且, 在上,以点为圆心的圆经过, 两点.
(1)试判断直线与 的位置关系,并说明理由.
思路点拨(1)观察图形,猜想直线与 相切.
连接,已知是的半径,要证直线是
的切线,只要证明即可.由 ,
可知 ,因此需要证明 .
图53
解:直线与 相切.
理由如下:如图53,连接
,,
,.
.
.
是的半径,直线与 相切.
图9
(2)当,的半径为3时,求 的长.
解:在中,, ,
.
在 中,,设,则
.
思路点拨 (2),在中,且在 中,故可根据正弦的定义和勾股定理列方程求解.
考点专练
3.(2024·湖南·中考)
【问题背景】 已知点是半径为的上的定点,连接 ,将线
段绕点按逆时针方向旋转得到,连接 ,过点
作的切线,在直线上取点,使得 为锐角.
【初步感知】
(1)如图10,当 时,____ .
30
图10
提示:由题意,得.又, 是等边三角形..直线是的切线,.∴ .
【问题探究】
(2)以线段为对角线作矩形,使得边过点,连接 ,对
角线,相交于点 .
①如图11,当时,求证:无论 在给定的范围内如何变化,
总成立.
图11
证明:,
,∴ .
直线是的切线, .
.
图11
四边形 是矩形,,
.
.
在和中,,,,∴
四边形是矩形,
, .
②如图12,当,时,请补全图形,并求 及 的值.
图12
解:补全图形如图60.过点作于点 ,过点作于点,连接,在 中,,, ,
.
,
此时点在线段上.
图60
图60
,,,.
,.
.
在中,,设 ,则
.
在中, .
四边形是矩形,
. .
考点四 圆中有关几何图形面积的问题
名师指导 可运用转化思想求圆中几何图形的面积.如果所求面积的图形
是规则图形,那么可直接应用相关面积公式计算;如果所求面积的图形
不是规则图形,就要转化为规则图形求解.在圆中求规则图形的面积,
除了扇形,也会涉及求三角形的面积,可以利用圆中的各种垂直关系直
接用面积公式求解,也可以利用相似三角形的性质求解.
例4 (2025·江苏南通·中考改编)如图13,等腰三角形 的顶角 ,与底边相切于点,并与两腰, 分别相交于点,,连接, .
图13
(1)求证:四边形 是菱形.
思路点拨 (1)只要证明和 都是等边三角形,就可推出四边形 的四条边相等,从而证得结论.
证明:如图54,连接
与底边 相切于点,
,, .
又 ,,和都是等边三角形.
,
四边形 是菱形.
图54
(2)当 的半径为2时,求图中阴影部分的面积.
图13
图54
解:如图54,连接交于点
四边形 是菱形,, ,.
在中,, .
.
.
思路点拨 (2)根据图中阴影部分的面积扇形 的面积-菱形 的面积,进行计算即可.
考点专练
图14
4.(2024·四川内江·中考)如图14,是 的直径,
是的中点,过点作的垂线,垂足为点 .
(1)求证: .
证明:是的直径,.
, .
是的中点, .
.
(2)求证:是 的切线.
图14
证明:如图61,连接
,
,
,
是的半径,是 的切线.
图61
(3)已知, ,求阴影部分的面积.
图14
图61
解:如图61,连接,,与相交于点
是的直径,.
.
又 ,四边形是矩形.
∴
是的半径,是的中点, ,,即
,
.
.
∴ .
图61
考点五 与圆有关的综合实践题
名师指导 与圆有关的综合实践题,一般会涉及材料阅读或操作探究或
生活情境,在解这类题时,要仔细阅读题目,提取关键信息,或根据题
意动手操作,找到解题的关键点.这类题目一般阅读量较大、综合性较
强,需要运用多个知识点,在解此类题时,不要畏难,一个小问一个小
问地解决,通常小问之间会有所关联,可以类比迁移.
例5 (2024·江苏连云港·中考)
【问题情境】
(1)如图15,圆与大正方形的各边都相切,小正方形是圆的内接正方
形,那么大正方形面积是小正方形面积的几倍?小昕将小正方形绕圆心
旋转 (如图16),这时候就容易发现大正方形面积是小正方形面积
的___倍.由此可见,图形变化是解决问题的有效策略.
2
图15
图16
思路点拨(1)观察旋转后的图形,可发现大正方形面积-小正方形面积= 个直角三角形的面积,再结合勾股定理可得出两正方形的面积关系.
【操作实践】
(2)如图17,图①是一个对角线互相垂直的四边形,边,,, 之
间存在某种数量关系.小昕按图17所示步骤进行操作,并将最终图形抽
象成图18.请你结合整个变化过程,直接写出图18中以矩形内一点
为端点的四条线段之间的数量关系.
图17
图18
提示:如图55,设与交于点.因为 ,所以
,, ,
.所以 .结合图形变换,得
.
图55
解:
思路点拨 (2)图形变换前后,线段的长不变,类比第(1)题,结合勾股定理可得线段之间的数量关系.
【探究应用】
(3)如图19,在图17④的基础上,小昕将绕点 逆时针旋转,,他发现旋转过程中存在最大值.已知 ,,当最大时,求 的长.
图19
思路点拨 (3)由旋转可知,点在以点为圆心, 为半径的圆上运动.观察图形并想象当点沿运动时的大小变化,可知当与 相切时, 最大.再结合(2)的相关结论解题.
解:如图56,将绕点逆时针旋转,点在以点 为圆心,
为半径的圆上运动.
,为的一个定点.
当与 相切时,最大.
则此时
.
由(2)可知,
.
图56
(4)如图20,在中, ,点, 分别在边和上,连接,,.已知, ,求 的最小值.
图20
解:如图57,将沿对折,点的对应点为点,将 沿对折,点的对应点为点,连接,, .
图57
思路点拨 (4)可类比(2)中图形的变换,对图20进行一定变换,将 等量转换到同一直线上,则此时 的值最小.解题时,可运用前面小问的结论.
再将沿方向平移,使点与点重合,如图58,得 ,连接 .
结合图形变换,得.
当,, 三点共线时,的值最小,最小值为的长.
,, ,
.
∴的最小值为 .
图57
图58
考点专练
5.(2025·青海·中考模拟)综合与实践
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做
成圆形的呢?这里面有什么数学道理吗?带着这样的疑问,小青做了如
下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.
【探究一】
(1)将车轮设计成等边三角形,转动过程如图21,设其中心到顶点的
距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨
迹是,,圆心角 .此时中心轨迹最
高点是(即的中点),转动一次前后中心的连线是 (水平线).
请在图22中计算到的距离 .
图21
图22
解:如图62,连接
,为的中点, ,.
,是等边三角形.
∴
.
图62
【探究二】
(2)将车轮设计成正方形,转动过程如图23,设其中心到顶点的距离
是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是
,,圆心角 .此时中心轨迹最高点是
(即的中点),转动一次前后中心的连线是 (水平线).请在图
24中计算到的距离 .(结果保留根号)
图23
图24
解:,为的中点,, ,.
.
∴ .
图23
图24
【探究三】
(3)将车轮设计成正六边形,转动过程如图25(见下页),设其中心
到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,
中心的轨迹是,圆心角的度数是____.此时中心轨迹最高点是
(即的中点),转动一次前后中心的连线是 (水平线),在图26
中计算到的距离 _______.(结果保留根号)
图25
图26
【归纳推理】
(4)比较,, 大小:_____________.按此规律推理,车轮设计
成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线
(水平线)的距离______(填“越大”或“越小”).
越小
【得出结论】
(5)将车轮设计成圆形,转动过程如图27,其中心(即圆心)的轨迹
与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)
的距离 ___.这样车辆行驶平稳、没有颠簸感.因此,将车轮设计成圆
形最适合行驶.
0
图27
第28讲 与圆有关的综合题
靶向锤炼
靶向练
图1
1.(2024·山东济宁·中考节选)如图1, 内接于
,是上一点,是 外一点,
,,连接.当 时,
求 的长.
解: , ,即
.
在和中,, ,,
.
图2
2.教材变式[湘教版九下第68页例3变式](2024·江苏
盐城·中考)如图2,点在以为直径的 上,过点
作的切线,过点作,垂足为点 ,连接
, .
(1)求证: .
证明:连接
是的切线,
,
是的直径, .
∴
.
(2)已知,,求 的半径.
图2
解: ,, ,
, ,即.
.
的半径为 .
攻坚练
图3
3.(2024·甘肃兰州·中考)如图3, 内接于
,为的直径,点为 上一点,
,延长至点,使 .
(1)求证:是 的切线.
图76
证明:如图76,连接,则
为的直径, .
.
在R和中,,,
,
,即 ,
是 的半径, 是 的切线.
图3
(2)已知,,求 的长.
解: , .
由(1)知, .
由(1)知,又 ,
.
,
,即.
解得 (舍去)或.
.
4.(2025·山东烟台·中考模拟)如图4,在菱形中,对角线, 相交于点,经过,两点,交对角线于点,连接交于点 ,且 .
图4
(1)求证:是 的切线.
图77
证明:如图77,连接,则
, .
四边形是菱形,
.
∴ .又 是的半径, 是 的切线.
图4
(2)已知 的半径与菱形的边长之比为5∶8,求 的值.
解: ,, .
∴ .
设,则
∴
,
四边形是菱形, , .
∴
∴ .
5.(2024·宁夏·中考)如图5,是的外接圆,为直径,点 是的内心,连接并延长交于点,过点作 的切线交的延长线于点 .
图5
(1)求证: .
证明:如图78,连接,交于点
,
为 的内心,
图78
图78
为的直径, .
∴ .
为的切线且为 的半径, ,即 .
∴
.
图5
(2)连接,的半径为2, ,求阴影部分的面积.(结果用含 的式子表示)
图78
解:如图78,连接, , .
.
又 , .
∴ .
.
拔尖练
图6
6.(2024·山东潍坊·中考)
【问题提出】在绿化公园时,需要安装一定数量的自动喷
洒装置,定时喷水养护.某公司准备在一块边长为 的正
方形草坪(如图6)中安装自动喷洒装置,为了既节约安装
成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方
案.[说明:一个自动喷洒装置的喷洒范围是半径为 的圆面.喷洒覆
盖率,为待喷洒区域面积, 为待喷洒区域中的实际喷洒面积]
【数学建模】这个问题可以转化为用圆面覆盖正方形面积的数学问题.
图6
【探索发现】
图7
(1)如图7,在该草坪中心位置设计安装1个喷洒半径为
的自动喷洒装置,该方案的喷洒覆盖率______.
取
0.785
提示:当喷洒半径为 时,喷洒面积 ,正方形草坪的面积=.故喷洒覆盖率 .
(2)如图8,在该草坪内设计安装4个喷洒半径均为 的自动喷洒装置;
如图9,设计安装9个喷洒半径均为 的自动喷洒装置……此类推,如
图10,设计安装个喷洒半径均为 的自动喷洒装置.与(1)中的方
案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒
覆盖率?请判断并给出理由.
图8
图9
图10
解:对于任意的,喷洒面积 ,而草坪面积始终为.
因此,无论取何值,喷洒覆盖率始终为 .
这说明增加装置个数同时减小喷洒半径,对提高喷洒覆盖率不起作用.
图8
图9
图10
(3)如图11所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,
且使得该草坪的喷洒覆盖率.已知 ,设
,的面积为,求关于的函数解析式,并求当
取得最小值时 的值.
图11
图11
解:连接,要使喷洒覆盖率,即 ,其中为草坪面积,为喷洒面积.
, ,,都经过正方形的中心点
,,
, 为的直径,即.
在 中,由勾股定得,得
.
当 时,取得最小值,此时,解得 (负值已舍去).
【问题解决】
图6
(4)该公司现有喷洒半径为 的自动喷洒装置若干个,
至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率
?(直接写出结果即可)
提示:由(3)可得,当的面积最小时, 为边长
为的正方形的外接圆.当 时,圆的内接正方形
解:至少安装9个这样的喷洒装置可使该草坪的喷洒覆盖率 .
的边长为,而草坪的边长为, ,即将草
坪分为9个正方形,将半径为 的自动喷洒装置放置于
9个正方形的中心,此时所用装置个数最少.故至少安装9个
这样的喷洒装置可使该草坪的喷洒覆盖率 .
图6
同课章节目录
