《基础卷》——第五单元圆(含解析)-2025-2026学年六年级上册数学(人教版)
文档属性
| 名称 | 《基础卷》——第五单元圆(含解析)-2025-2026学年六年级上册数学(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 204.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
《基础卷》——第五单元圆(单元测试)-2025-2026学年六年级上册数学(人教版)
一、单选题
1.在一张长10cm,宽8cm的长方形纸上画一个最大的圆,圆的半径是( )。
A.6cm B.8cm C.4cm
2.一个圆的直径扩大2倍,它的周长就( ),面积就( )。
A.扩大2倍,扩大2倍 B.扩大2倍,扩大4倍 C.扩大4倍,扩大4倍
3.把一个圆沿着半径平均分成若干份,然后拼成一个近似的长方形,量得这个长方形的宽是2cm,这个圆的周长是( )cm。
A.3.14 B.6.28 C.12.56 D.25.02
4.下列说法正确的是( )
A.周长相等的两个圆,面积也相等
B.π等于3.14
C.一个半圆形钢板半径是1dm,周长是3.14dm
D.直径为5dm的圆要比半径为4dm的圆大
5.从甲地到乙地有A、B两条路线可以走(如下图),这两条路线相比,( )。
A.同样长 B.A 路线长 C.B 路线长
6.一个长方形、一个正方形和一个圆的周长都是314厘米,( )的面积最大。
A.长方形 B.正方形 C.圆
7.如右图,从A点到B点有三条路,每条路都是由一个或两个半圆组成的。比较这三条路的长度,( )。
A.最上面的路最长 B.最上面的路最短
C.三条路长度相等 D.不确定
8.在一个长1.25米,宽0.8米的长方形里,最多能剪( )个半径为20厘米的圆。
A.5 B.7 C.6 D.24
二、判断题
9.圆的半径由3cm增加到6cm,圆的面积增加了27πcm2。(
)
10.所有的直径都相等,所有的半径也都相等。( )
11.如果大圆的半径等于小圆的直径,那么大圆的周长是小圆的4倍。( )
12.如果一个正方形和一个圆的周长相等,则圆的面积大。( )
13.半圆形的面积等于半圆形所在的这个圆面积的一半。( )
14.通过转化的方法,探索出了分数除法和圆面积的计算方法.( )
15.用同样长的绳子分别围成正方形和圆,圆的面积比正方形的面积大。( )
16.在面积相等的长方形、正方形和圆中,周长最长的是长方形。( )
三、填空题
17.在周长是16厘米的正方形内,画一个尽可能大的圆,这个圆的面积是 平方厘米。
18.有大小两个圆,小圆的半径是3厘米,大圆的半径是6厘米,它们的周长之比是 ,面积之比是 。
19.有大小两个圆,如果大圆的半径是小圆半径的3倍,那么大圆的周长是小圆周长的 倍,大圆的面积是小圆面积的 倍。
20.图中圆的半径是 cm,长方形的面积是 cm2。
21.在大圆内剪两个大小一样的小圆做杯垫。已知小圆的半径为4厘米,那么大圆的面积是 平方厘米。
22.要画一个周长是31.4cm的圆,圆规两脚间的距离是 cm,这个圆的面积是 平方厘米。
23.下图中,阴影部分的周长是 厘米,面积是 平方厘米。
24.用一根绳子围绕大树,如果绕10圈则剩下3米,如果绕12圈又缺3米,那么绕8圈剩下 米。
四、操作题
25.在下面的正方形中画一个最大的扇形,并计算出扇形的周长和面积。
五、解决问题
26.一个圆形花坛的半径是3米,它的面积是多少平方米?
27.刘奶奶有一段长 10.99米的铁栅栏,现在她要用这段铁栅栏围成一个半圆形的鸡舍 ,其中一面利用一面长7米的墙,如图,请你帮刘奶奶算一算,这面墙的长度够吗?如果够,围成鸡舍的面积是多少?(保留两位小数)
28.一个车轮的外直径为0.86m,如果车轮5分钟转120周,车子每分钟前进多少米
29.一根铁丝正好能围成直径是6厘米的圆,如果把它围成一个正方形,则这个正方形的边长是多少?
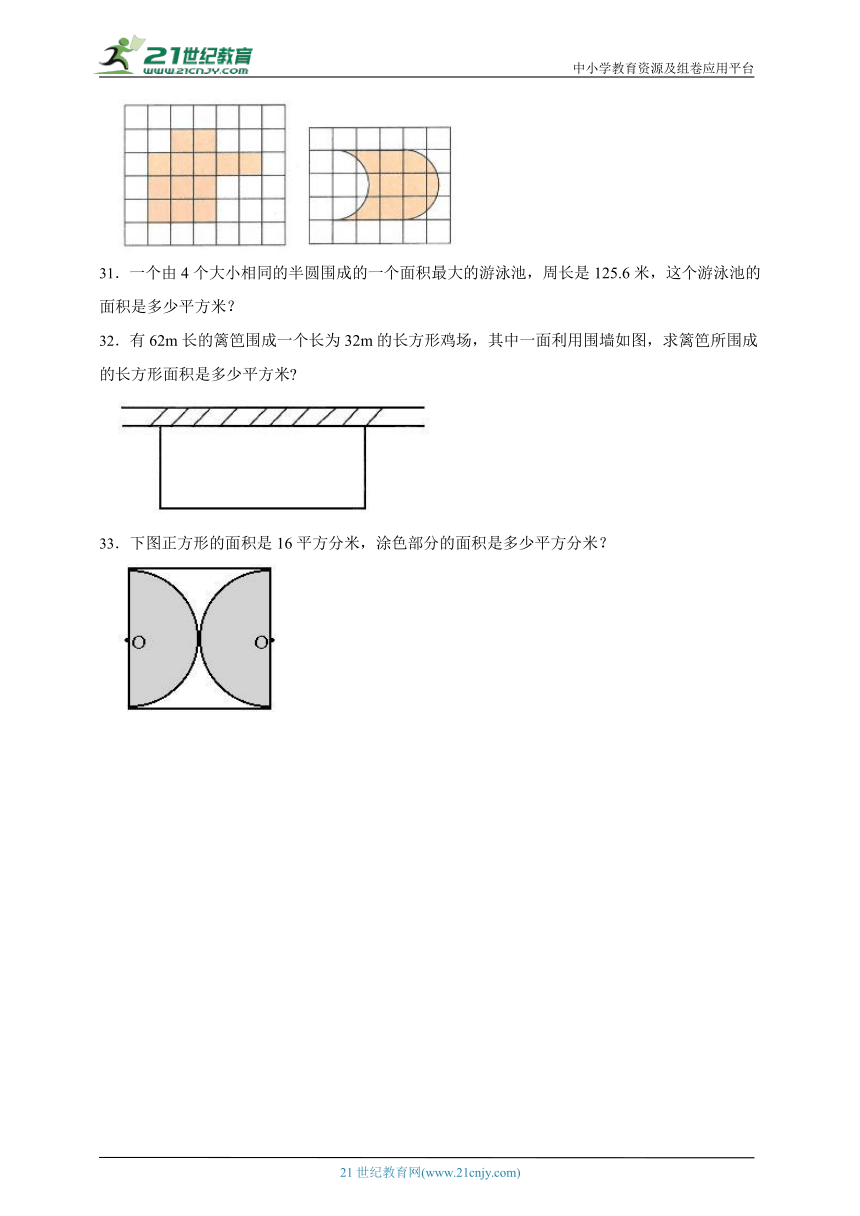
30.观察下面的图形,怎样求它们的周长比较简便?它们的周长各是多少厘米?(每个小方格的边长是1厘米)
31.一个由4个大小相同的半圆围成的一个面积最大的游泳池,周长是125.6米,这个游泳池的面积是多少平方米?
32.有62m长的篱笆围成一个长为32m的长方形鸡场,其中一面利用围墙如图,求篱笆所围成的长方形面积是多少平方米
33.下图正方形的面积是16平方分米,涂色部分的面积是多少平方分米?
答案解析部分
1.【答案】C
【解析】【解答】解:8÷2=4(cm)
故答案为:C。
【分析】在长方形中画一个最大的圆,圆的直径=长方形的宽,所以圆的半径=圆的直径÷2。
2.【答案】B
【解析】【解答】 一个圆的直径扩大2倍,它的周长就扩大2倍,面积就扩大4倍。
故答案为:B。
【分析】根据圆的周长和面积公式可知,圆的周长公式:C=2πr,圆的面积公式:S=πr2,一个圆的直径扩大a倍,它的半径也扩大a倍,则它的周长就扩大a倍,面积就扩大a2倍。
3.【答案】C
4.【答案】A
【解析】【解答】解:A项:周长相等的两个圆,面积也相等,原题干说法正确;
B项:π约等于3.14,原题干说法错误;
C项:1×3.14+2×1
=3.14+2
=5.14(分米),原题干说法错误;
D项:4×2=8(分米),5分米<8分米,直径为5dm的圆要比半径为4dm的圆小,原题干说法错误。
故答案为:A。
【分析】A项:周长相等的两个圆,那么半径就相等,半径相等面积也相等;
B项:π约等于3.14;
C项:半圆的周长=半径×π+半径×2;
D项:圆的直径=半径×2,直径大的圆面积就大。
5.【答案】A
【解析】【解答】解:设大圆的直径为D,小圆的直径为d,则D=2d
A的路线为:
B的路线为:
因为
所以A和B两条路线的距离相等。
故答案为:A
【分析】观察图形,可知,A所走的路线是以甲地到乙地直线距离为直径的圆的周长的一半,B所走的路线是以甲地到乙地直线距离为直径的圆的周长,根据圆的周长公式即可判断
6.【答案】C
【解析】【解答】解:长方形的长+宽=314÷2=157(厘米),
所以长方形的长和宽越接近时,面积越大则长方形的长为79厘米,宽为78厘米,
则长方形的面积=79×78=6162(平方厘米);
正方形的边长=314÷4=78.5(厘米),
正方形的面积=78.5×78.5=6162.25(平方厘米);
圆的半径=314÷3.14÷2
=100÷2
=50(厘米),
圆的面积=3.14×502
=3.14×2500
=7850(平方厘米);
因为6162<6162.25<7850,所以圆的面积最大。
故答案为:C。
【分析】长方形的周长=(长+宽)×2,长方形的面积=长×宽;正方形的周长=正方形的边长×4,正方形的面积=正方形的边长×正方形的边长;圆的周长=π×圆的半径×2,圆的面积=π×圆的半径的平方;长方形的长和宽越接近长方形的面积越大,本题分别计算出长方形、正方形和圆的面积,比较即可得出答案。
7.【答案】C
【解析】【解答】解:最上方的路的长度=π×AB的长度÷2;
中间的路的长度=π×AB长度的一半÷2×2=π×AB的长度÷2;
最下方的路的长度=π×左边圆的直径÷2+π×(AB的长度-左边圆的直径)÷2
=π×AB的长度÷2,
所以三条路的长度相等。
故答案为:C。
【分析】圆的周长=π×圆的直径,本题中分别根据圆的直径公式分别计算出三条线路的长度,再比较即可得出答案。
8.【答案】C
【解析】【解答】解:1.25米=125厘米
0.8米=80厘米
20×2=40(厘米)
125÷40=3(个)······5(厘米)
80÷40=2(个)
3×2=6(个)。
故答案为:C。
【分析】先单位换算,最多能剪圆的个数=(长方形的长÷圆的直径) ×(长方形的宽÷圆的直径);其中,圆的直径=半径×2。
9.【答案】正确
【解析】【解答】解:π×6×6=36π(平方厘米)
π×3×3=9π(平方厘米)
36π-9π=27π(平方厘米)
故答案为:正确。
【分析】圆的面积=π×半径的平方。
10.【答案】错误
【解析】【解答】解:在同一个圆中,所有的直径都相等,所有的半径也都相等。
故答案为:错误。
【分析】同一个圆的直径相等,半径也相等。
11.【答案】错误
【解析】【解答】 解:如果大圆的半径等于小圆的直径,也就是大圆的直径是小圆直径的2倍,那么大圆的周长等于小圆周长的2倍。因此,题干中的结论是错误的。
故答案为:错误。
【分析】根据圆的周长公式:C=πd,如果大圆的半径等于小圆的直径,也就是大圆的直径是小圆直径的2倍,那么大圆的周长等于小圆周长的2倍。据此判断。
12.【答案】正确
【解析】【解答】解:如果一个正方形和一个圆的周长相等,则圆的面积大,说法正确。
故答案为:正确。
【分析】假设周长为C。正方形的边长=C÷4=,则正方形的面积=边长×边长=×=;圆的半径=C÷3.14÷2=,则圆的面积=πr2=3.14××=。因为分子相同都是C2,并且16>12.56,所以<,即正方形的面积小于圆的面积,所以原题干说法正确。
13.【答案】正确
【解析】【解答】解:半圆形的面积等于半圆形所在的这个圆面积的一半,原题说法正确;
故答案为:正确。
【分析】圆的面积公式为:S=πr2,半圆形的面积=πr2÷2,可以看出半圆的面积确实等于它所在圆面积的一半,据此判断即可。
14.【答案】正确
【解析】【解答】解:“转化”是小学阶段研究平面图形面积的计算方法常用的思想方法,如:探索平行四边形面积的计算方法时,把平行四边形转化成了长方形,然后由长方形的面积推导出了平行四边形的面积计算方法;探索圆面积的计算方法时,把圆拼成了一个近似的长方形,长方形的长近似于圆周长的一半,宽近似于圆的半径,从而推导出圆的面积计算方法······都是通过转化得来的;另外,在学习了倒数之后,探索分数除法的计算方法,也是通过转化,除以一个不为0的数,转化为乘这个数的倒数。
因此,通过转化的方法,探索出了分数除法和圆面积的计算方法.此说法是正确的。
故答案为:正确。
【分析】“转化”是小学阶段研究平面图形面积的计算方法常用的思想方法,在探索圆面积计算方法时,就是把圆转化为长方形,转化后只是形状变了,但面积不变.另外,在学习了倒数之后,探索分数除法的计算方法,也是通过转化,除以一个不为0的数,转化为乘这个数的倒数,据此判断。
15.【答案】正确
【解析】【解答】 设绳子的长度为L,
L÷4=,
S正方形=()2=,
L÷(2π)=,
S圆=π()2==,
<,
那么圆的面积比正方形的面积大。
故答案为:正确
【分析】先分别求出正方形的边长和圆的半径,再根据面积公式计算面积,最后进行比较, 同分母分数大小比较,分子大的分数较大,分子小的分数较小。
16.【答案】正确
【解析】【解答】解:设三种图形的面积均为4,则正方形的边长为2,周长为2×4=8;
圆的半径的平方为4÷3.14≈1,半径也约等于1,周长约为 2×3.14×1=6.28;此时正方形的周长比圆的周长长;
假设长方形的宽是1,长就是4,周长就是(1+4)×2=10,综合比较,长方形的周长最长。
故答案为:正确。
【分析】本题可以先假设出面积为4,然后分析对比正方形和圆的周长。对于长方形,可以假设出长和宽,也可以分析“当两个整数的积相等时,这两个数相等时其和最小,因此长方形与正方形面积相等,长方形的周长比正方形的周长长,所以面积相等的长方形、正方形和圆中,周长最长的是长方形”。
17.【答案】12.56
【解析】【解答】解:16÷4=4(厘米)
4÷2=2(厘米)
3.14×22=12.56(平方厘米)。
故答案为:12.56。
【分析】在正方形内画一个尽可能大的圆,这个圆的直径与正方形的边长相等,这个圆的面积=π×半径2。
18.【答案】1∶2;1∶4
【解析】【解答】解:小圆的周长:大圆的周长=小圆的半径:大圆的半径=3:6=1:2;
小圆的面积:大圆的面积=小圆的半径2:大圆的半径2=32:62
=9:36
=1:4。
故答案为:1:2;1:4。
【分析】圆的周长=π×圆的半径×2,所以圆的周长之比=半径之比;圆的面积=π×圆的半径的平方,所以圆的周长之比=半径之比的平方,本题据此解答。
19.【答案】3;9
【解析】【解答】解:3÷1=3
3×3=9。
故答案为:3;9。
【分析】两个圆的周长比等于它们半径的比;面积比等于它们半径平方的比。
20.【答案】4;96
【解析】【解答】解:半径:12÷3=4(cm),长方形面积:12×(4×2)=96(cm2)。
故答案为:4;96。
【分析】长方形的长相当于半径的3倍,所以用12除以3即可求出半径;长方形的宽是半径的2倍,先确定长方形的宽,再计算面积即可。
21.【答案】200.96
22.【答案】5;78.5
【解析】【解答】解:31.4÷3.14÷2
=10÷2
=5(cm)
圆的面积=3.14×52
=3.14×25
=78.5(cm2)
故答案为:5;78.5。
【分析】圆规两脚间的距离=圆的半径=圆的周长÷π÷2,圆的面积=π×半径的平方,代入数值计算即可。
23.【答案】3π+2(或11.42); π(或4.71)
【解析】【解答】解:阴影部分的周长=3.14×(2×2)÷2+2+3.14×2÷2
=6.28+2+3.14
=11.42(厘米);
阴影部分的面积=3.14×22÷2-3.14×(2÷2)2÷2
=6.28-1.57
=4.71(平方厘米)。
故答案为:11.42;4.71。
【分析】观察图形可得大半圆的半径是小半圆的直径,阴影部分的周长=大半圆周长的一半+大半圆的半径-小半圆周长的一半,半圆的周长=π×直径÷2;阴影部分的面积=大半圆的面积-小半圆的面积,半圆的面积=π×圆的半径的平方÷2,代入数值计算即可。
24.【答案】9
【解析】【解答】 解:设树每圈绕x米,
12x-3=10x+3
12x-3-10x=10x+3-10x
2x-3=3
2x-3+3=3+3
2x=6
2x÷2=6÷2
x=3
绳子总长:
12×3-3
=36-3
=33(米)
绕8圈剩下:
33-8×3
=33-24
=9(米)
故答案为:9。
【分析】根据题意可知,无论绕几圈,这根绳子的总长是一定的,根据总长一定列方程解答,设树每圈绕x米,也就是树的横截面周长为x米,每圈的周长×12-3=每圈的周长×10+3,据此列方程可以求出绳子长度,然后用绳子的总长度-绕8圈的长度=剩下的长度,据此列式解答。
25.【答案】解:
周长:3.14×(5×2)÷4+5×2
=31.4÷4+10
=7.85+10
=17.85(厘米)
面积:3.14×52÷4
=78.5÷4
=19.625(平方厘米)
【解析】【分析】这个扇形的周长=π×半径×2÷4+半径×2;
这个扇形的面积=π×半径2÷4。
26.【答案】解: (平方米)。
答:圆形花坛的面积是28.26平方米。
【解析】【分析】圆面积公式:S=πr ,由此根据面积公式计算面积即可。
27.【答案】解:7×3.14÷2
=21.98÷2
=10.99(米)
(7÷2)2×3.14÷2
=38.465÷2
≈19.23(平方米)
答:够了,围成鸡舍的面积是19.23平方米。
【解析】【分析】这个鸡舍需要栅栏的长度=墙的长度×π÷2,经过计算刚好是铁栅栏的长度,所以够了,那么围成鸡舍的面积=(墙的长度÷2)2×π÷2。
28.【答案】解:0.86×3.14×(120÷5)
=2.704×24
=64.8096(m)
答:车子每分钟前进64.8096米。
【解析】【分析】用120除以5求出每分钟转的周数。用车轮的直径乘3.14求出车轮的周长,用车轮的周长乘每分钟转的圈数即可求出车子每分钟前进的长度。
29.【答案】解:3.14×6÷4=18.84÷4=4.71(厘米)
答:正方形的边长是4.71厘米。
【解析】【分析】圆的周长=π×圆的直径,圆的周长就是正方形的周长,正方形的周长÷4=正方形的边长,据此解答。
30.【答案】解:用“转化”的策略求它们的周长比较简便。
左边图形的周长:(4+5)×2=18(厘米)
右边图形的周长:3×2+3.14×3=15.42(厘米)
【解析】【解答】解:图一:18×1=18(厘米)
图二:3×2+3.14×3=15.42(厘米)
【分析】图一的周长=小正方形边长的个数×平均每个小正方形的边长;
利用平移的方法,图二的周长=长×2+直径3厘米的圆的周长;其中,圆的周长=π×直径。
31.【答案】解:125.6÷2=62.8(米)62.8÷3.14÷2=10(米)(10×2)2+3.14×102×2=400+628=1028(平方米)答:这个游泳池的面积是1028平方米。
【解析】【分析】这四个半圆中间是一个正方形,正方形的边长与圆的直径相等。用游泳池的周长除以2求出一个圆的周长,用一个圆的周长除以3.14再除以2求出半径。把两个圆的面积加上中间正方形的面积就是游泳池的总面积。
32.【答案】480平方米
【解析】【解答】(62-32)÷2
=30÷2
=15(米)
32×15=480(平方米)
答:篱笆所围成的长方形面积是480平方米。
【分析】用篱笆的长减去鸡场的长即可求出鸡场的两条宽的和,除以2即可求出它的一条宽,要求它的面积时,则直接用它的长乘宽即可。
33.【答案】解:
∵4×4=16
∴d=4
=4×3.14
=12.56(平方分米)
答:涂色部分的面积是12.56平方分米。
【解析】【分析】正方形的边长与圆的直径相等,正方形面积=边长×边长,根据正方形面积公式先判断出正方形的边长,然后根据圆面积公式计算面积即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《基础卷》——第五单元圆(单元测试)-2025-2026学年六年级上册数学(人教版)
一、单选题
1.在一张长10cm,宽8cm的长方形纸上画一个最大的圆,圆的半径是( )。
A.6cm B.8cm C.4cm
2.一个圆的直径扩大2倍,它的周长就( ),面积就( )。
A.扩大2倍,扩大2倍 B.扩大2倍,扩大4倍 C.扩大4倍,扩大4倍
3.把一个圆沿着半径平均分成若干份,然后拼成一个近似的长方形,量得这个长方形的宽是2cm,这个圆的周长是( )cm。
A.3.14 B.6.28 C.12.56 D.25.02
4.下列说法正确的是( )
A.周长相等的两个圆,面积也相等
B.π等于3.14
C.一个半圆形钢板半径是1dm,周长是3.14dm
D.直径为5dm的圆要比半径为4dm的圆大
5.从甲地到乙地有A、B两条路线可以走(如下图),这两条路线相比,( )。
A.同样长 B.A 路线长 C.B 路线长
6.一个长方形、一个正方形和一个圆的周长都是314厘米,( )的面积最大。
A.长方形 B.正方形 C.圆
7.如右图,从A点到B点有三条路,每条路都是由一个或两个半圆组成的。比较这三条路的长度,( )。
A.最上面的路最长 B.最上面的路最短
C.三条路长度相等 D.不确定
8.在一个长1.25米,宽0.8米的长方形里,最多能剪( )个半径为20厘米的圆。
A.5 B.7 C.6 D.24
二、判断题
9.圆的半径由3cm增加到6cm,圆的面积增加了27πcm2。(
)
10.所有的直径都相等,所有的半径也都相等。( )
11.如果大圆的半径等于小圆的直径,那么大圆的周长是小圆的4倍。( )
12.如果一个正方形和一个圆的周长相等,则圆的面积大。( )
13.半圆形的面积等于半圆形所在的这个圆面积的一半。( )
14.通过转化的方法,探索出了分数除法和圆面积的计算方法.( )
15.用同样长的绳子分别围成正方形和圆,圆的面积比正方形的面积大。( )
16.在面积相等的长方形、正方形和圆中,周长最长的是长方形。( )
三、填空题
17.在周长是16厘米的正方形内,画一个尽可能大的圆,这个圆的面积是 平方厘米。
18.有大小两个圆,小圆的半径是3厘米,大圆的半径是6厘米,它们的周长之比是 ,面积之比是 。
19.有大小两个圆,如果大圆的半径是小圆半径的3倍,那么大圆的周长是小圆周长的 倍,大圆的面积是小圆面积的 倍。
20.图中圆的半径是 cm,长方形的面积是 cm2。
21.在大圆内剪两个大小一样的小圆做杯垫。已知小圆的半径为4厘米,那么大圆的面积是 平方厘米。
22.要画一个周长是31.4cm的圆,圆规两脚间的距离是 cm,这个圆的面积是 平方厘米。
23.下图中,阴影部分的周长是 厘米,面积是 平方厘米。
24.用一根绳子围绕大树,如果绕10圈则剩下3米,如果绕12圈又缺3米,那么绕8圈剩下 米。
四、操作题
25.在下面的正方形中画一个最大的扇形,并计算出扇形的周长和面积。
五、解决问题
26.一个圆形花坛的半径是3米,它的面积是多少平方米?
27.刘奶奶有一段长 10.99米的铁栅栏,现在她要用这段铁栅栏围成一个半圆形的鸡舍 ,其中一面利用一面长7米的墙,如图,请你帮刘奶奶算一算,这面墙的长度够吗?如果够,围成鸡舍的面积是多少?(保留两位小数)
28.一个车轮的外直径为0.86m,如果车轮5分钟转120周,车子每分钟前进多少米
29.一根铁丝正好能围成直径是6厘米的圆,如果把它围成一个正方形,则这个正方形的边长是多少?
30.观察下面的图形,怎样求它们的周长比较简便?它们的周长各是多少厘米?(每个小方格的边长是1厘米)
31.一个由4个大小相同的半圆围成的一个面积最大的游泳池,周长是125.6米,这个游泳池的面积是多少平方米?
32.有62m长的篱笆围成一个长为32m的长方形鸡场,其中一面利用围墙如图,求篱笆所围成的长方形面积是多少平方米
33.下图正方形的面积是16平方分米,涂色部分的面积是多少平方分米?
答案解析部分
1.【答案】C
【解析】【解答】解:8÷2=4(cm)
故答案为:C。
【分析】在长方形中画一个最大的圆,圆的直径=长方形的宽,所以圆的半径=圆的直径÷2。
2.【答案】B
【解析】【解答】 一个圆的直径扩大2倍,它的周长就扩大2倍,面积就扩大4倍。
故答案为:B。
【分析】根据圆的周长和面积公式可知,圆的周长公式:C=2πr,圆的面积公式:S=πr2,一个圆的直径扩大a倍,它的半径也扩大a倍,则它的周长就扩大a倍,面积就扩大a2倍。
3.【答案】C
4.【答案】A
【解析】【解答】解:A项:周长相等的两个圆,面积也相等,原题干说法正确;
B项:π约等于3.14,原题干说法错误;
C项:1×3.14+2×1
=3.14+2
=5.14(分米),原题干说法错误;
D项:4×2=8(分米),5分米<8分米,直径为5dm的圆要比半径为4dm的圆小,原题干说法错误。
故答案为:A。
【分析】A项:周长相等的两个圆,那么半径就相等,半径相等面积也相等;
B项:π约等于3.14;
C项:半圆的周长=半径×π+半径×2;
D项:圆的直径=半径×2,直径大的圆面积就大。
5.【答案】A
【解析】【解答】解:设大圆的直径为D,小圆的直径为d,则D=2d
A的路线为:
B的路线为:
因为
所以A和B两条路线的距离相等。
故答案为:A
【分析】观察图形,可知,A所走的路线是以甲地到乙地直线距离为直径的圆的周长的一半,B所走的路线是以甲地到乙地直线距离为直径的圆的周长,根据圆的周长公式即可判断
6.【答案】C
【解析】【解答】解:长方形的长+宽=314÷2=157(厘米),
所以长方形的长和宽越接近时,面积越大则长方形的长为79厘米,宽为78厘米,
则长方形的面积=79×78=6162(平方厘米);
正方形的边长=314÷4=78.5(厘米),
正方形的面积=78.5×78.5=6162.25(平方厘米);
圆的半径=314÷3.14÷2
=100÷2
=50(厘米),
圆的面积=3.14×502
=3.14×2500
=7850(平方厘米);
因为6162<6162.25<7850,所以圆的面积最大。
故答案为:C。
【分析】长方形的周长=(长+宽)×2,长方形的面积=长×宽;正方形的周长=正方形的边长×4,正方形的面积=正方形的边长×正方形的边长;圆的周长=π×圆的半径×2,圆的面积=π×圆的半径的平方;长方形的长和宽越接近长方形的面积越大,本题分别计算出长方形、正方形和圆的面积,比较即可得出答案。
7.【答案】C
【解析】【解答】解:最上方的路的长度=π×AB的长度÷2;
中间的路的长度=π×AB长度的一半÷2×2=π×AB的长度÷2;
最下方的路的长度=π×左边圆的直径÷2+π×(AB的长度-左边圆的直径)÷2
=π×AB的长度÷2,
所以三条路的长度相等。
故答案为:C。
【分析】圆的周长=π×圆的直径,本题中分别根据圆的直径公式分别计算出三条线路的长度,再比较即可得出答案。
8.【答案】C
【解析】【解答】解:1.25米=125厘米
0.8米=80厘米
20×2=40(厘米)
125÷40=3(个)······5(厘米)
80÷40=2(个)
3×2=6(个)。
故答案为:C。
【分析】先单位换算,最多能剪圆的个数=(长方形的长÷圆的直径) ×(长方形的宽÷圆的直径);其中,圆的直径=半径×2。
9.【答案】正确
【解析】【解答】解:π×6×6=36π(平方厘米)
π×3×3=9π(平方厘米)
36π-9π=27π(平方厘米)
故答案为:正确。
【分析】圆的面积=π×半径的平方。
10.【答案】错误
【解析】【解答】解:在同一个圆中,所有的直径都相等,所有的半径也都相等。
故答案为:错误。
【分析】同一个圆的直径相等,半径也相等。
11.【答案】错误
【解析】【解答】 解:如果大圆的半径等于小圆的直径,也就是大圆的直径是小圆直径的2倍,那么大圆的周长等于小圆周长的2倍。因此,题干中的结论是错误的。
故答案为:错误。
【分析】根据圆的周长公式:C=πd,如果大圆的半径等于小圆的直径,也就是大圆的直径是小圆直径的2倍,那么大圆的周长等于小圆周长的2倍。据此判断。
12.【答案】正确
【解析】【解答】解:如果一个正方形和一个圆的周长相等,则圆的面积大,说法正确。
故答案为:正确。
【分析】假设周长为C。正方形的边长=C÷4=,则正方形的面积=边长×边长=×=;圆的半径=C÷3.14÷2=,则圆的面积=πr2=3.14××=。因为分子相同都是C2,并且16>12.56,所以<,即正方形的面积小于圆的面积,所以原题干说法正确。
13.【答案】正确
【解析】【解答】解:半圆形的面积等于半圆形所在的这个圆面积的一半,原题说法正确;
故答案为:正确。
【分析】圆的面积公式为:S=πr2,半圆形的面积=πr2÷2,可以看出半圆的面积确实等于它所在圆面积的一半,据此判断即可。
14.【答案】正确
【解析】【解答】解:“转化”是小学阶段研究平面图形面积的计算方法常用的思想方法,如:探索平行四边形面积的计算方法时,把平行四边形转化成了长方形,然后由长方形的面积推导出了平行四边形的面积计算方法;探索圆面积的计算方法时,把圆拼成了一个近似的长方形,长方形的长近似于圆周长的一半,宽近似于圆的半径,从而推导出圆的面积计算方法······都是通过转化得来的;另外,在学习了倒数之后,探索分数除法的计算方法,也是通过转化,除以一个不为0的数,转化为乘这个数的倒数。
因此,通过转化的方法,探索出了分数除法和圆面积的计算方法.此说法是正确的。
故答案为:正确。
【分析】“转化”是小学阶段研究平面图形面积的计算方法常用的思想方法,在探索圆面积计算方法时,就是把圆转化为长方形,转化后只是形状变了,但面积不变.另外,在学习了倒数之后,探索分数除法的计算方法,也是通过转化,除以一个不为0的数,转化为乘这个数的倒数,据此判断。
15.【答案】正确
【解析】【解答】 设绳子的长度为L,
L÷4=,
S正方形=()2=,
L÷(2π)=,
S圆=π()2==,
<,
那么圆的面积比正方形的面积大。
故答案为:正确
【分析】先分别求出正方形的边长和圆的半径,再根据面积公式计算面积,最后进行比较, 同分母分数大小比较,分子大的分数较大,分子小的分数较小。
16.【答案】正确
【解析】【解答】解:设三种图形的面积均为4,则正方形的边长为2,周长为2×4=8;
圆的半径的平方为4÷3.14≈1,半径也约等于1,周长约为 2×3.14×1=6.28;此时正方形的周长比圆的周长长;
假设长方形的宽是1,长就是4,周长就是(1+4)×2=10,综合比较,长方形的周长最长。
故答案为:正确。
【分析】本题可以先假设出面积为4,然后分析对比正方形和圆的周长。对于长方形,可以假设出长和宽,也可以分析“当两个整数的积相等时,这两个数相等时其和最小,因此长方形与正方形面积相等,长方形的周长比正方形的周长长,所以面积相等的长方形、正方形和圆中,周长最长的是长方形”。
17.【答案】12.56
【解析】【解答】解:16÷4=4(厘米)
4÷2=2(厘米)
3.14×22=12.56(平方厘米)。
故答案为:12.56。
【分析】在正方形内画一个尽可能大的圆,这个圆的直径与正方形的边长相等,这个圆的面积=π×半径2。
18.【答案】1∶2;1∶4
【解析】【解答】解:小圆的周长:大圆的周长=小圆的半径:大圆的半径=3:6=1:2;
小圆的面积:大圆的面积=小圆的半径2:大圆的半径2=32:62
=9:36
=1:4。
故答案为:1:2;1:4。
【分析】圆的周长=π×圆的半径×2,所以圆的周长之比=半径之比;圆的面积=π×圆的半径的平方,所以圆的周长之比=半径之比的平方,本题据此解答。
19.【答案】3;9
【解析】【解答】解:3÷1=3
3×3=9。
故答案为:3;9。
【分析】两个圆的周长比等于它们半径的比;面积比等于它们半径平方的比。
20.【答案】4;96
【解析】【解答】解:半径:12÷3=4(cm),长方形面积:12×(4×2)=96(cm2)。
故答案为:4;96。
【分析】长方形的长相当于半径的3倍,所以用12除以3即可求出半径;长方形的宽是半径的2倍,先确定长方形的宽,再计算面积即可。
21.【答案】200.96
22.【答案】5;78.5
【解析】【解答】解:31.4÷3.14÷2
=10÷2
=5(cm)
圆的面积=3.14×52
=3.14×25
=78.5(cm2)
故答案为:5;78.5。
【分析】圆规两脚间的距离=圆的半径=圆的周长÷π÷2,圆的面积=π×半径的平方,代入数值计算即可。
23.【答案】3π+2(或11.42); π(或4.71)
【解析】【解答】解:阴影部分的周长=3.14×(2×2)÷2+2+3.14×2÷2
=6.28+2+3.14
=11.42(厘米);
阴影部分的面积=3.14×22÷2-3.14×(2÷2)2÷2
=6.28-1.57
=4.71(平方厘米)。
故答案为:11.42;4.71。
【分析】观察图形可得大半圆的半径是小半圆的直径,阴影部分的周长=大半圆周长的一半+大半圆的半径-小半圆周长的一半,半圆的周长=π×直径÷2;阴影部分的面积=大半圆的面积-小半圆的面积,半圆的面积=π×圆的半径的平方÷2,代入数值计算即可。
24.【答案】9
【解析】【解答】 解:设树每圈绕x米,
12x-3=10x+3
12x-3-10x=10x+3-10x
2x-3=3
2x-3+3=3+3
2x=6
2x÷2=6÷2
x=3
绳子总长:
12×3-3
=36-3
=33(米)
绕8圈剩下:
33-8×3
=33-24
=9(米)
故答案为:9。
【分析】根据题意可知,无论绕几圈,这根绳子的总长是一定的,根据总长一定列方程解答,设树每圈绕x米,也就是树的横截面周长为x米,每圈的周长×12-3=每圈的周长×10+3,据此列方程可以求出绳子长度,然后用绳子的总长度-绕8圈的长度=剩下的长度,据此列式解答。
25.【答案】解:
周长:3.14×(5×2)÷4+5×2
=31.4÷4+10
=7.85+10
=17.85(厘米)
面积:3.14×52÷4
=78.5÷4
=19.625(平方厘米)
【解析】【分析】这个扇形的周长=π×半径×2÷4+半径×2;
这个扇形的面积=π×半径2÷4。
26.【答案】解: (平方米)。
答:圆形花坛的面积是28.26平方米。
【解析】【分析】圆面积公式:S=πr ,由此根据面积公式计算面积即可。
27.【答案】解:7×3.14÷2
=21.98÷2
=10.99(米)
(7÷2)2×3.14÷2
=38.465÷2
≈19.23(平方米)
答:够了,围成鸡舍的面积是19.23平方米。
【解析】【分析】这个鸡舍需要栅栏的长度=墙的长度×π÷2,经过计算刚好是铁栅栏的长度,所以够了,那么围成鸡舍的面积=(墙的长度÷2)2×π÷2。
28.【答案】解:0.86×3.14×(120÷5)
=2.704×24
=64.8096(m)
答:车子每分钟前进64.8096米。
【解析】【分析】用120除以5求出每分钟转的周数。用车轮的直径乘3.14求出车轮的周长,用车轮的周长乘每分钟转的圈数即可求出车子每分钟前进的长度。
29.【答案】解:3.14×6÷4=18.84÷4=4.71(厘米)
答:正方形的边长是4.71厘米。
【解析】【分析】圆的周长=π×圆的直径,圆的周长就是正方形的周长,正方形的周长÷4=正方形的边长,据此解答。
30.【答案】解:用“转化”的策略求它们的周长比较简便。
左边图形的周长:(4+5)×2=18(厘米)
右边图形的周长:3×2+3.14×3=15.42(厘米)
【解析】【解答】解:图一:18×1=18(厘米)
图二:3×2+3.14×3=15.42(厘米)
【分析】图一的周长=小正方形边长的个数×平均每个小正方形的边长;
利用平移的方法,图二的周长=长×2+直径3厘米的圆的周长;其中,圆的周长=π×直径。
31.【答案】解:125.6÷2=62.8(米)62.8÷3.14÷2=10(米)(10×2)2+3.14×102×2=400+628=1028(平方米)答:这个游泳池的面积是1028平方米。
【解析】【分析】这四个半圆中间是一个正方形,正方形的边长与圆的直径相等。用游泳池的周长除以2求出一个圆的周长,用一个圆的周长除以3.14再除以2求出半径。把两个圆的面积加上中间正方形的面积就是游泳池的总面积。
32.【答案】480平方米
【解析】【解答】(62-32)÷2
=30÷2
=15(米)
32×15=480(平方米)
答:篱笆所围成的长方形面积是480平方米。
【分析】用篱笆的长减去鸡场的长即可求出鸡场的两条宽的和,除以2即可求出它的一条宽,要求它的面积时,则直接用它的长乘宽即可。
33.【答案】解:
∵4×4=16
∴d=4
=4×3.14
=12.56(平方分米)
答:涂色部分的面积是12.56平方分米。
【解析】【分析】正方形的边长与圆的直径相等,正方形面积=边长×边长,根据正方形面积公式先判断出正方形的边长,然后根据圆面积公式计算面积即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
