第一章 《三角形》章节知识点复习题(含答案)苏科版八年级数学上册
文档属性
| 名称 | 第一章 《三角形》章节知识点复习题(含答案)苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 13:39:47 | ||
图片预览



文档简介
第一章 《三角形》章节知识点复习题
1.下列各组长度的线段中,能组成三角形的是( )
A.2,3,5 B.3、5、9 C.3,6,9 D.3、7、9
2.如图,已知,小明以点B为圆心,为半径画弧线,又以点A为圆心,m为半径画弧线,两弧交于点C,然后连接,,得到 ABC,则m的值不可能是( )
A.1 B.2 C.6 D.10
3.综合与实践:
【回归教材】
八年级上册教材中探究了“三角形中边与角之间的不等关系”,部分内容如下:
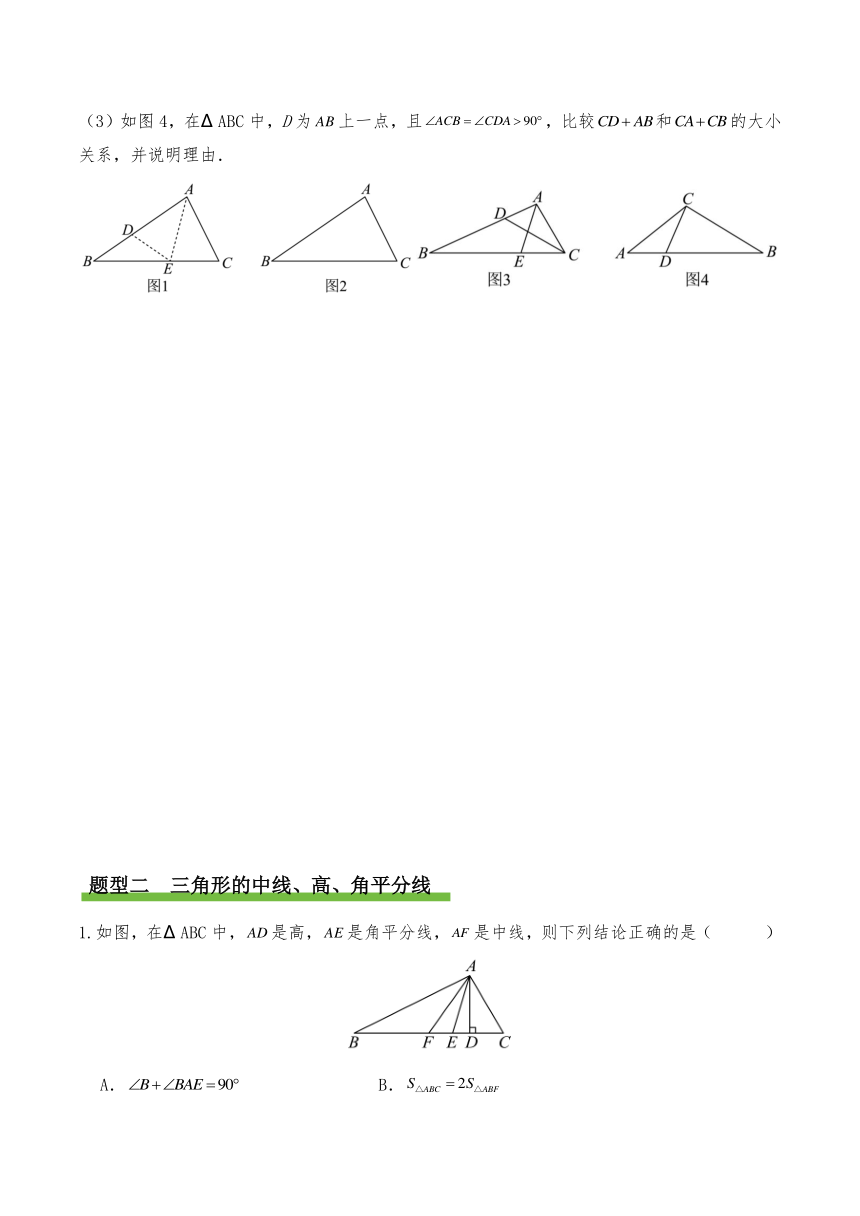
如图1,在 ABC中,如果,那么我们可以将 ABC折叠,折边落在上,点C落在上的为D点,折线交于点E,则,,
这说明在一个三角形中,如果两条边不等,那么它们所对的角也不等.
大边所对的角越大.
从上面的过程可以看出,通过轴对称的性质或“截长补短”构建全等三角形的方法将陌生问题转化为已学习的问题,这是研究几何问题时常用的方法.
类比探究“在三角形中,大角对大边”.
(1)如图2,在 ABC中,,判断: ______(填“>”、“=”或“<”).
【进阶思考】
(2)如图3,在 ABC中,,、分别为、的角平分线,求证:.
【拓展运用】
(3)如图4,在 ABC中,D为上一点,且,比较和的大小关系,并说明理由.
1.如图,在 ABC中,是高,是角平分线,是中线,则下列结论正确的是( )
A. B.
C. D.
2.如图,在 ABC中,中线和中线相交于点,若的面积为36,则四边形的面积为 .
3.已知:如图,在中,,分别是斜边上的高和中线,是的平分线,某同学想直接得到点B到直线的距离,那么他应该测量线段 的长度.
1.如图, BFD≌ CED,若的面积为3,的面积为2,则的面积为( )
A.3 B.5 C.7 D.9
2.如图,,若,,,则 BDF的周长等于 .
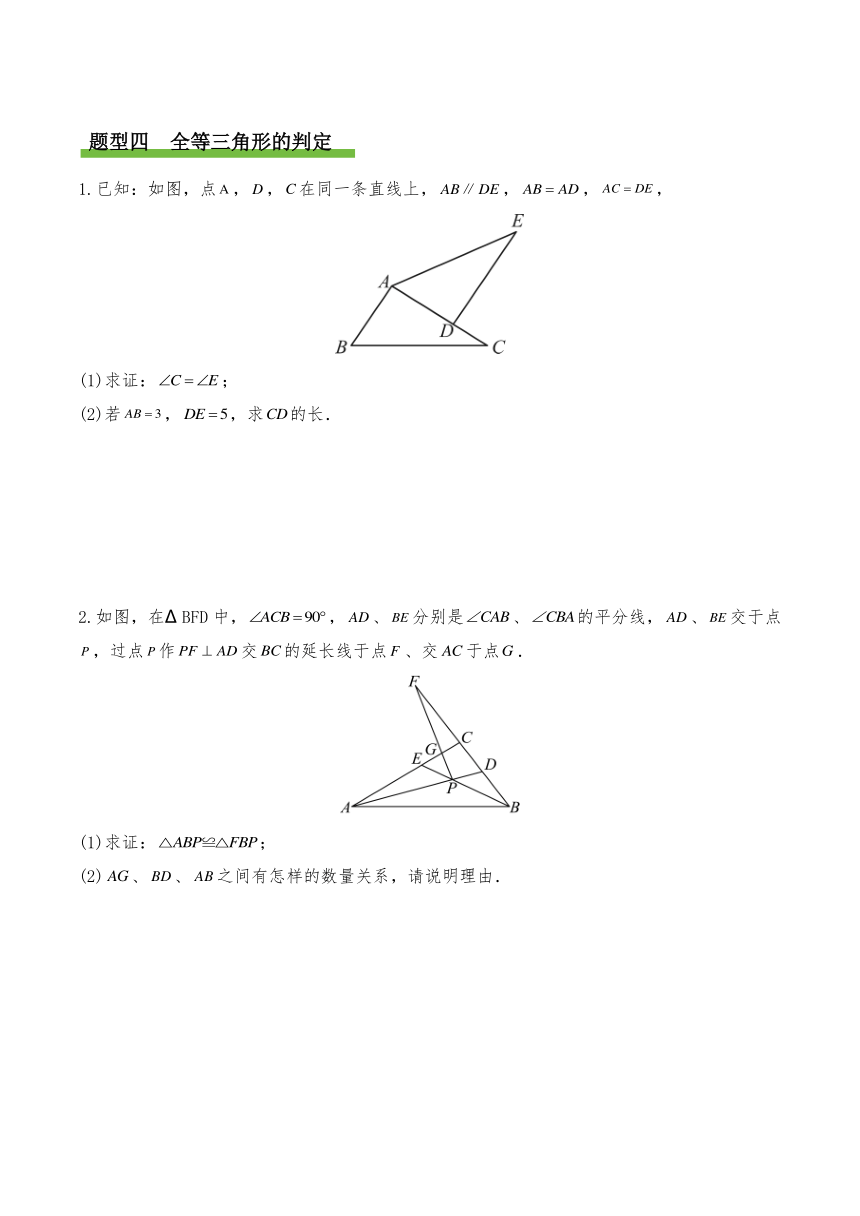
1.已知:如图,点,,在同一条直线上,,,,
(1)求证:;
(2)若,,求的长.
2.如图,在 BFD中,,、分别是、的平分线,、交于点,过点作交的延长线于点、交于点.
(1)求证:;
(2)、、之间有怎样的数量关系,请说明理由.
3.(1)如图1,在 ABC中,,,直线经过点,分别从点,向直线作垂线,垂足分别为,,求证:;
【变式探究】
(2)如图2,在 ABC中,,直线经过点,点,分别在直线上,如果,猜想,,有何数量关系,并给予证明;
【拓展应用】
(3)小明和科技兴趣小组的同学制作了一幅机器人图案,大致图形如图3所示,以 ABC的边,为一边向外作和,其中,,,是边上的高,延长交于点.设的面积为,的面积为,请猜想,大小关系,并说明理由.
1.如图,在 ABC中,,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线交于点D,连接,若,,则的周长为( )
A.17 B.16 C.18 D.20
2.我们把两组邻边分别相等的四边形称之为“筝形”.在四边形中,对角线交于点O.下列条件中,不能判断四边形是筝形的是( )
A., B.,
C., D.,
3.如图,在 ABC中,,,的垂直平分线交于点D,交于点E,连接.若,则的长为 .
1.如图,在 ABC中,边的垂直平分线与 ABC的外角平分线交于点P,过点P作于点D,于点E.若,.则的长度是 .
2.如图,在锐角三角形中,是边上的高,在,上分别截取线段,,使;分别以点E,F为圆心,大于的长为半径画弧,在内,两弧交于点P,作射线,交于点M,过点M作于点N.若,则 .
3.如图,在 ABC中,,平分,于,下列结论:①;②;③;④;⑤ BDE与的面积之比即与的长度之比.其中正确的是 .
1.如图,在 ABC中,点E、F分别在上,是的垂直平分线,,,交于点G.
(1)求证:平分;
(2)若,求证:.
2.如图,在中,,,是的垂直平分线,垂足为点,交于点,连接.
(1)求证:平分;
(2)若,求的长.
3.如图, ABC中,,的平分线与边的垂直平分线相交于D,交的延长线于E,于F,现有下列结论:①;②;③;④;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
1.如图,将 ABC绕点逆时针旋转得到 ADE,点在上.已知,则的大小为( )
A. B. C. D.
2.小明在学习“等腰三角形两底角相等”时,他猜想“等腰三角形底角的平分线相等”.请补全已知、求证,并进行证明,验证小明的猜想.
已知:如图,在 ABC中,__________
求证:__________
证明:
2.如图,在 ABC中,,D为射线上一动点(不与点B、C重合),在的右侧作 ADE,使得,连接.
(1)若,则______.
(2)当点D在线段上时,求证:;
(3)若点D运动到线段上某一点时,恰好有,问:线段与线段有什么位置关系并说明理由.
1.如图, ABC是等边三角形,E,F分别是边上的点,且且交于点P,且垂足为G.
(1)求证:;
(2)若求的长度.
2.已知:如图,分别以的两条直角边为边作等边三角形和等边三角形,连接,且点在线段上.
(1)求证:;
(2)求证:.
3.如图,在等边 ABC中,为边上一点,为上一点,且,连接与相交于点.
(1)与的数量关系是,与构成的锐角夹角的度数是;并说明理由.
(2)深入探究,将图中的延长至点,使,连接,,如图所示.求证:平分(第一问的结论,本问可直接使用)
【例10】如图, ABC中,,点D在上,,延长至点E,使,过点E作于点F,交于点G,若,则的值是( )
A. B. C. D.
2.如图, ABC是等边三角形,点D是的中点,于点E,若,则的长为( )
A.12 B.9 C.8 D.6
3.如图,等边三角形的边长为9,为边上一动点,为延长线上一动点,交于点,点为中点.若,则长为( )
A.2 B.3 C.4 D.5
参考答案
1.D
【知识点】构成三角形的条件
【分析】本题考查了三角形三边关系,解题的关键是掌握“三角形任意两边之和大于第三边,任意两边之差小于第三边”.
根据三角形三边关系定理,任意两边之和大于第三边.只需验证每组中最小的两边之和是否大于最大边即可.
【详解】A.2,3,5:最小两边和为,等于最大边5,不满足两边之和大于第三边,不能组成三角形;
B.3,5,9:最小两边和为,小于最大边9,不满足条件,不能组成三角形;
C.3,6,9:最小两边和为,等于最大边9,不满足条件,不能组成三角形;
D.3,7,9:最小两边和为,大于最大边9,满足条件,能组成三角形.
故选D.
2.A
【知识点】作线段(尺规作图)、确定第三边的取值范围
【分析】本题考查三角形的三边关系,根据三边关系求出的范围,进行判断即可.
【详解】解:由作图可知:,
∵,
∴,即:;
∴m的值不可能是1,
故选A.
3.解:(1)如图2,在内作,交于点,
∴,
∴
∵,
∴;
(2)如图3,延长到点,使,连接,
∴,,
又∵,
∴,
∵,,
∴∠B=∠DCB,,
∴,
∴,
在和中,
∴
∴,
∴.
1.B
【知识点】与三角形的高有关的计算问题、根据三角形中线求面积、三角形角平分线的定义
【分析】本题考查了中线、角平分线和中线的定义,直角三角形的性质,熟练掌握知识点是解题的关键.分别根据三角形的中线意义和性质可判断B和D;根据三角形高的定义,直角三角形两锐角互余判断A;根据三角形角平分线的意义可判断C.
【详解】解:∵是中线,
∴,故D选项不正确,不符合题意;
∴,故B选项正确,符合题意;
∵是高,
∴,
∴,故A选项不正确,不符合题意;
∵是角平分线,
∴,故C选项不正确,不符合题意;
故选:B.
2.12
【知识点】根据三角形中线求面积
【分析】本题考查了三角形的面积,熟记三角形的中线把三角形分成面积相等的两个三角形是解题的关键.
根据等底等高的三角形的面积相等可知三角形的中线把三角形分成面积相等的两个三角形,然后表示出,得出,再由中线的性质得出即可求解.
【详解】解:∵、是的中线,
∴,
∵,,
∴,
连接并延长交于点K,如图所示:
∴为中线,
∴,
∵,
∴,
同理得:,
∴,
∵ ABC的面积为36,
∴,
∴四边形的面积为,
故答案为:12.
3.
【知识点】点到直线的距离、画三角形的高、根据三角形中线求长度、三角形角平分线的定义
【分析】本题考查点到直线的距离,根据点到直线的距离为垂线段的长,进行作答即可.
【详解】解:由题意,得:,
∴,
∴点B到直线的距离为线段的长,
故他应该测量线段的长;
故答案为:.
1.C
【知识点】根据三角形中线求面积、全等三角形的性质
【分析】本题主要考查全等三角形的性质,三角形中线的性质,先计算出,再根据三角形的中线将三角形分成面积相等的两部分得到接着根据全等三角形的性质得到,然后计算即可.
【详解】解:∵ BFD≌ CED,
∴,
∵
∴,
∵,
∴,
∴.
故选:C.
2.13
【知识点】全等三角形的性质
【分析】本题考查了全等三角形性质的运用,运用全等三角形的性质,找对对应边,即可得 BDF三边边长,然后根据三角形的周长公式求解即可.
【详解】解:∵,,
∴,,,
∴ BDF的周长为.
故答案为:13.
1.(1)∵
∴
∵,,
∴
∴;
(2)∵
∴,
∴.
2.(1)证明:分别是的平分线,
.
,
.
又,
.
同理,.
.
在和中,
.
(2)解:,理由如下:
由(1)得,
∴,
在和中,
,
.
.
,
.
3.(1)证明:∵直线l,直线l,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴;
(2)解:,,的数量关系是:,证明如下:
∵是的外角,
∴∠EAB=∠ADB+∠DBA,
∴∠EAC+∠BAC=∠ADB+∠DBA,
∵,
∴,
在和中,
,
∴,
∴,,
∴;
(3),大小关系是:,理由如下:
过点D作交的延长线于点M,过点E作于点N,如图所示:
∵,
∴∠AGB=∠M=90°,
∴,
∵,
∴∠BAG+∠DAM=90°,,
∴∠ABG=∠DAM,
在和中,
,
∴,
∴,
同理可证明:,
∴,
∴,
∵,,
∴.
1.D
【知识点】线段垂直平分线的性质、作垂线(尺规作图)
【分析】本题考查作图,线段垂直平分线、线段垂直平分线的性质.由题意可得垂直且平分,根据垂直平分线的性质可得,从而可得,求解即可.
【详解】解:由作图痕迹可得,垂直且平分,
,
,
故选:D.
2.D
【知识点】全等三角形综合问题、线段垂直平分线的性质
【分析】本题考查了线段垂直平分线的判定和性质以及全等三角形的判定与性质等知识;
根据线段垂直平分线的判定和性质可判断A选项,证明可判断B、C选项,由,不能判断,即可判断D选项,进而可得答案.
【详解】解:A、∵,,
∴垂直平分,
∴,
∴四边形是筝形;
B、∵,,,
∴,
∴,
∴四边形是筝形;
C、∵,,,
∴,
∴,,
∴四边形是筝形;
D、由,不能判断,,故不能判断四边形是筝形;
故选:D.
3.解:∵,,是的垂直平分线,
∴,
∴,
∵,
∴,
故答案为:.
1.2
【知识点】全等的性质和HL综合(HL)、角平分线的性质定理、线段垂直平分线的性质
【分析】本题考查了角平分线的性质、垂直平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线上的点到角两边距离相等,垂直平分线上的点到线段两端距离相等.
连接,通过证明,得出,再证明,得出,即可解答.
【详解】解:连接,
∵平分,,,
∴,
在和中,
,
∴,
∴,
∵是的垂直平分线,
∴,
在和中,
,
∴,
∴,
又∵,,
∴,
整理得:,
∴,
故答案为:2.
2.9
【知识点】角平分线的性质定理、作角平分线(尺规作图)
【分析】本题考查了尺规作图-作已知角的平分线,角平分线的性质,根据作图步骤可判断平分,根据角平分线的性质可得出,结合已知即可求解.
【详解】解∶由作图知∶ 平分,
∵,,,
∴,
又,
∴,
∴,
故答案为∶9.
3.①②③
【知识点】全等的性质和HL综合(HL)、角平分线的性质定理
【分析】根据角平分线的性质,即可判断①;通过证明即可得到,即可判断②;根据直角三角形的两个锐角互余即可判断③;根据已知条件无法证明即可判断④;根据两个三角形的高相等,面积比就等于底的比即可判断⑤.
【详解】解:①∵,平分,,
∴,故①正确;
②在和中,
,
∴,
∴,
∴,故②正确;
③在中,在中,
∴,故③正确;
④无法证明,故④错误;
∵ BDE和中,
∴,
∵,
∴ BDE与的面积之比不等于与的长度之比,故⑤错误;
综上分析可知:正确的有①②③.
故答案为:①②③.
1.(1)证明:∵是的垂直平分线,
∴,
∵,,
∴平分;
(2)解:∵,
∴,
∵是的垂直平分线,
∴,
∴,
∴,
∴,,
∴,
∴.
2.(1)证明:∵是的垂直平分线,
∴,
∴.
∵,,
∴,
∴,
∴平分.
(2)解:∵平分,,,
∴.
∵,,
∴.
∵,,
∴.
3.D
【知识点】全等的性质和HL综合(HL)、角平分线的性质定理、线段垂直平分线的性质、含30度角的直角三角形
【分析】由角平分线的性质可知①正确;②由题意可知,故此可知,,从而可证明②正确;连接,然后证明,从而得到,从而可证明③④.
【详解】解:如图所示:连接.
①∵平分,,,
∴,∴①正确.
②∵,平分,
∴,
∵,,
∴,
∵,,
∴,,
∴,∴②正确.
∵是的垂直平分线,
∴,
在和中,
,
∴,
∴,
∴,
又∵,,
∴,故③④正确.
故选:D.
1.C
【知识点】等边对等角、根据旋转的性质求解
【分析】本题考查的是旋转的性质,等腰三角形的性质,掌握“旋转前后的对应角相等与等边对等角”是解本题的关键.先由旋转的性质证明,,再利用等边对等角证明,从而可得答案.
【详解】解:将绕点逆时针旋转得到,点在上,
,,
,
,
,,
,
故选:C.
2.已知:如图,在 ABC中,,,平分和交,于点F,E,
求证:
证明:∵,
∴,
又∵,平分和,
∴,,
∴,
又∵,
∴,
∴.
3.(1)解:∵,,
∴,
∴,
∴,
∵,
∴;
(2)证明:,
,
.
在和中.
,
;
(3).理由如下:
由(2)知,
.
,
.
,
.
为等边三角形,
,
,
,
.
1.(1)证明:∵ ABC是等边三角形,
∴,
在与 CBF中,
∴,
∴;
(2)解:∵,
∴,
∵,即,
∴,
∴在中, ,
∵,
∴.
2.(1)证明:∵ ABD, EBC是等边三角形,
∴,
∴
∴
∴;
(2)∵ ABC是直角三角形,为直角边,
∴
∵ BEC是等边三角形,则,
∴,
由(1)可得
∴
∵是等边三角形,
∴
∴
∴
∴
∴垂直平分
∴.
3.(1)∵ ABC是等边三角形,
,
在和中,
,
,
,
,
故答案为:,;
(2)证明:由(1)可知,,
,
,
∴是等边三角形,
,
∵ ABC是等边三角形,
,
,
,
即,
,
,
,
,
平分.
1.D
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、含30度角的直角三角形
【分析】本题考查了全等三角形的判定和性质,直角三角形的性质,由“”可证,可得,由直角三角形的性质可得,,由线段的数量关系可求解,添加恰当辅助线构造全等三角形是解题的关键.
【详解】解:如图,过点作于,
,,,
,
在和中,
,
,
,
,,,
,
,,
,
,
,
,
,
故选:D.
2.A
【知识点】含30度角的直角三角形、等边三角形的性质
【分析】本题考查等边三角形的性质,掌握等边三角形的性质和含角的直角三角形的性质是解题的关键.
由等边三角形的性质及中点的定义得,,再根据直角三角形两锐角互余得,最后根据含角的直角三角形的性质即可得出答案.
【详解】解:∵ ABC是等边三角形,点是的中点,
∴,,
∵,,
∴,
∴,
∴,
∴,
∴
故选:A.
3.B
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、含30度角的直角三角形、等边三角形的性质
【分析】过点D作,交于F,先证 CDF是等边三角形,再证 PDF≌ PEB,得,设,则,最后根据在直角三角形中,的角所对的边是斜边的一半,计算,即可.
【详解】解:如下图,过点D作,交于F,
是等边三角形,
,
,
,
是等边三角形,
,
点P为中点,
,
在和中,
,
,
,
,
,
,
,
设,则,
,
解得:,
,
故选:B.
1.下列各组长度的线段中,能组成三角形的是( )
A.2,3,5 B.3、5、9 C.3,6,9 D.3、7、9
2.如图,已知,小明以点B为圆心,为半径画弧线,又以点A为圆心,m为半径画弧线,两弧交于点C,然后连接,,得到 ABC,则m的值不可能是( )
A.1 B.2 C.6 D.10
3.综合与实践:
【回归教材】
八年级上册教材中探究了“三角形中边与角之间的不等关系”,部分内容如下:
如图1,在 ABC中,如果,那么我们可以将 ABC折叠,折边落在上,点C落在上的为D点,折线交于点E,则,,
这说明在一个三角形中,如果两条边不等,那么它们所对的角也不等.
大边所对的角越大.
从上面的过程可以看出,通过轴对称的性质或“截长补短”构建全等三角形的方法将陌生问题转化为已学习的问题,这是研究几何问题时常用的方法.
类比探究“在三角形中,大角对大边”.
(1)如图2,在 ABC中,,判断: ______(填“>”、“=”或“<”).
【进阶思考】
(2)如图3,在 ABC中,,、分别为、的角平分线,求证:.
【拓展运用】
(3)如图4,在 ABC中,D为上一点,且,比较和的大小关系,并说明理由.
1.如图,在 ABC中,是高,是角平分线,是中线,则下列结论正确的是( )
A. B.
C. D.
2.如图,在 ABC中,中线和中线相交于点,若的面积为36,则四边形的面积为 .
3.已知:如图,在中,,分别是斜边上的高和中线,是的平分线,某同学想直接得到点B到直线的距离,那么他应该测量线段 的长度.
1.如图, BFD≌ CED,若的面积为3,的面积为2,则的面积为( )
A.3 B.5 C.7 D.9
2.如图,,若,,,则 BDF的周长等于 .
1.已知:如图,点,,在同一条直线上,,,,
(1)求证:;
(2)若,,求的长.
2.如图,在 BFD中,,、分别是、的平分线,、交于点,过点作交的延长线于点、交于点.
(1)求证:;
(2)、、之间有怎样的数量关系,请说明理由.
3.(1)如图1,在 ABC中,,,直线经过点,分别从点,向直线作垂线,垂足分别为,,求证:;
【变式探究】
(2)如图2,在 ABC中,,直线经过点,点,分别在直线上,如果,猜想,,有何数量关系,并给予证明;
【拓展应用】
(3)小明和科技兴趣小组的同学制作了一幅机器人图案,大致图形如图3所示,以 ABC的边,为一边向外作和,其中,,,是边上的高,延长交于点.设的面积为,的面积为,请猜想,大小关系,并说明理由.
1.如图,在 ABC中,,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线交于点D,连接,若,,则的周长为( )
A.17 B.16 C.18 D.20
2.我们把两组邻边分别相等的四边形称之为“筝形”.在四边形中,对角线交于点O.下列条件中,不能判断四边形是筝形的是( )
A., B.,
C., D.,
3.如图,在 ABC中,,,的垂直平分线交于点D,交于点E,连接.若,则的长为 .
1.如图,在 ABC中,边的垂直平分线与 ABC的外角平分线交于点P,过点P作于点D,于点E.若,.则的长度是 .
2.如图,在锐角三角形中,是边上的高,在,上分别截取线段,,使;分别以点E,F为圆心,大于的长为半径画弧,在内,两弧交于点P,作射线,交于点M,过点M作于点N.若,则 .
3.如图,在 ABC中,,平分,于,下列结论:①;②;③;④;⑤ BDE与的面积之比即与的长度之比.其中正确的是 .
1.如图,在 ABC中,点E、F分别在上,是的垂直平分线,,,交于点G.
(1)求证:平分;
(2)若,求证:.
2.如图,在中,,,是的垂直平分线,垂足为点,交于点,连接.
(1)求证:平分;
(2)若,求的长.
3.如图, ABC中,,的平分线与边的垂直平分线相交于D,交的延长线于E,于F,现有下列结论:①;②;③;④;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
1.如图,将 ABC绕点逆时针旋转得到 ADE,点在上.已知,则的大小为( )
A. B. C. D.
2.小明在学习“等腰三角形两底角相等”时,他猜想“等腰三角形底角的平分线相等”.请补全已知、求证,并进行证明,验证小明的猜想.
已知:如图,在 ABC中,__________
求证:__________
证明:
2.如图,在 ABC中,,D为射线上一动点(不与点B、C重合),在的右侧作 ADE,使得,连接.
(1)若,则______.
(2)当点D在线段上时,求证:;
(3)若点D运动到线段上某一点时,恰好有,问:线段与线段有什么位置关系并说明理由.
1.如图, ABC是等边三角形,E,F分别是边上的点,且且交于点P,且垂足为G.
(1)求证:;
(2)若求的长度.
2.已知:如图,分别以的两条直角边为边作等边三角形和等边三角形,连接,且点在线段上.
(1)求证:;
(2)求证:.
3.如图,在等边 ABC中,为边上一点,为上一点,且,连接与相交于点.
(1)与的数量关系是,与构成的锐角夹角的度数是;并说明理由.
(2)深入探究,将图中的延长至点,使,连接,,如图所示.求证:平分(第一问的结论,本问可直接使用)
【例10】如图, ABC中,,点D在上,,延长至点E,使,过点E作于点F,交于点G,若,则的值是( )
A. B. C. D.
2.如图, ABC是等边三角形,点D是的中点,于点E,若,则的长为( )
A.12 B.9 C.8 D.6
3.如图,等边三角形的边长为9,为边上一动点,为延长线上一动点,交于点,点为中点.若,则长为( )
A.2 B.3 C.4 D.5
参考答案
1.D
【知识点】构成三角形的条件
【分析】本题考查了三角形三边关系,解题的关键是掌握“三角形任意两边之和大于第三边,任意两边之差小于第三边”.
根据三角形三边关系定理,任意两边之和大于第三边.只需验证每组中最小的两边之和是否大于最大边即可.
【详解】A.2,3,5:最小两边和为,等于最大边5,不满足两边之和大于第三边,不能组成三角形;
B.3,5,9:最小两边和为,小于最大边9,不满足条件,不能组成三角形;
C.3,6,9:最小两边和为,等于最大边9,不满足条件,不能组成三角形;
D.3,7,9:最小两边和为,大于最大边9,满足条件,能组成三角形.
故选D.
2.A
【知识点】作线段(尺规作图)、确定第三边的取值范围
【分析】本题考查三角形的三边关系,根据三边关系求出的范围,进行判断即可.
【详解】解:由作图可知:,
∵,
∴,即:;
∴m的值不可能是1,
故选A.
3.解:(1)如图2,在内作,交于点,
∴,
∴
∵,
∴;
(2)如图3,延长到点,使,连接,
∴,,
又∵,
∴,
∵,,
∴∠B=∠DCB,,
∴,
∴,
在和中,
∴
∴,
∴.
1.B
【知识点】与三角形的高有关的计算问题、根据三角形中线求面积、三角形角平分线的定义
【分析】本题考查了中线、角平分线和中线的定义,直角三角形的性质,熟练掌握知识点是解题的关键.分别根据三角形的中线意义和性质可判断B和D;根据三角形高的定义,直角三角形两锐角互余判断A;根据三角形角平分线的意义可判断C.
【详解】解:∵是中线,
∴,故D选项不正确,不符合题意;
∴,故B选项正确,符合题意;
∵是高,
∴,
∴,故A选项不正确,不符合题意;
∵是角平分线,
∴,故C选项不正确,不符合题意;
故选:B.
2.12
【知识点】根据三角形中线求面积
【分析】本题考查了三角形的面积,熟记三角形的中线把三角形分成面积相等的两个三角形是解题的关键.
根据等底等高的三角形的面积相等可知三角形的中线把三角形分成面积相等的两个三角形,然后表示出,得出,再由中线的性质得出即可求解.
【详解】解:∵、是的中线,
∴,
∵,,
∴,
连接并延长交于点K,如图所示:
∴为中线,
∴,
∵,
∴,
同理得:,
∴,
∵ ABC的面积为36,
∴,
∴四边形的面积为,
故答案为:12.
3.
【知识点】点到直线的距离、画三角形的高、根据三角形中线求长度、三角形角平分线的定义
【分析】本题考查点到直线的距离,根据点到直线的距离为垂线段的长,进行作答即可.
【详解】解:由题意,得:,
∴,
∴点B到直线的距离为线段的长,
故他应该测量线段的长;
故答案为:.
1.C
【知识点】根据三角形中线求面积、全等三角形的性质
【分析】本题主要考查全等三角形的性质,三角形中线的性质,先计算出,再根据三角形的中线将三角形分成面积相等的两部分得到接着根据全等三角形的性质得到,然后计算即可.
【详解】解:∵ BFD≌ CED,
∴,
∵
∴,
∵,
∴,
∴.
故选:C.
2.13
【知识点】全等三角形的性质
【分析】本题考查了全等三角形性质的运用,运用全等三角形的性质,找对对应边,即可得 BDF三边边长,然后根据三角形的周长公式求解即可.
【详解】解:∵,,
∴,,,
∴ BDF的周长为.
故答案为:13.
1.(1)∵
∴
∵,,
∴
∴;
(2)∵
∴,
∴.
2.(1)证明:分别是的平分线,
.
,
.
又,
.
同理,.
.
在和中,
.
(2)解:,理由如下:
由(1)得,
∴,
在和中,
,
.
.
,
.
3.(1)证明:∵直线l,直线l,
∴,
∴,
∵,
∴,
∴,
在和中,
,
∴;
(2)解:,,的数量关系是:,证明如下:
∵是的外角,
∴∠EAB=∠ADB+∠DBA,
∴∠EAC+∠BAC=∠ADB+∠DBA,
∵,
∴,
在和中,
,
∴,
∴,,
∴;
(3),大小关系是:,理由如下:
过点D作交的延长线于点M,过点E作于点N,如图所示:
∵,
∴∠AGB=∠M=90°,
∴,
∵,
∴∠BAG+∠DAM=90°,,
∴∠ABG=∠DAM,
在和中,
,
∴,
∴,
同理可证明:,
∴,
∴,
∵,,
∴.
1.D
【知识点】线段垂直平分线的性质、作垂线(尺规作图)
【分析】本题考查作图,线段垂直平分线、线段垂直平分线的性质.由题意可得垂直且平分,根据垂直平分线的性质可得,从而可得,求解即可.
【详解】解:由作图痕迹可得,垂直且平分,
,
,
故选:D.
2.D
【知识点】全等三角形综合问题、线段垂直平分线的性质
【分析】本题考查了线段垂直平分线的判定和性质以及全等三角形的判定与性质等知识;
根据线段垂直平分线的判定和性质可判断A选项,证明可判断B、C选项,由,不能判断,即可判断D选项,进而可得答案.
【详解】解:A、∵,,
∴垂直平分,
∴,
∴四边形是筝形;
B、∵,,,
∴,
∴,
∴四边形是筝形;
C、∵,,,
∴,
∴,,
∴四边形是筝形;
D、由,不能判断,,故不能判断四边形是筝形;
故选:D.
3.解:∵,,是的垂直平分线,
∴,
∴,
∵,
∴,
故答案为:.
1.2
【知识点】全等的性质和HL综合(HL)、角平分线的性质定理、线段垂直平分线的性质
【分析】本题考查了角平分线的性质、垂直平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线上的点到角两边距离相等,垂直平分线上的点到线段两端距离相等.
连接,通过证明,得出,再证明,得出,即可解答.
【详解】解:连接,
∵平分,,,
∴,
在和中,
,
∴,
∴,
∵是的垂直平分线,
∴,
在和中,
,
∴,
∴,
又∵,,
∴,
整理得:,
∴,
故答案为:2.
2.9
【知识点】角平分线的性质定理、作角平分线(尺规作图)
【分析】本题考查了尺规作图-作已知角的平分线,角平分线的性质,根据作图步骤可判断平分,根据角平分线的性质可得出,结合已知即可求解.
【详解】解∶由作图知∶ 平分,
∵,,,
∴,
又,
∴,
∴,
故答案为∶9.
3.①②③
【知识点】全等的性质和HL综合(HL)、角平分线的性质定理
【分析】根据角平分线的性质,即可判断①;通过证明即可得到,即可判断②;根据直角三角形的两个锐角互余即可判断③;根据已知条件无法证明即可判断④;根据两个三角形的高相等,面积比就等于底的比即可判断⑤.
【详解】解:①∵,平分,,
∴,故①正确;
②在和中,
,
∴,
∴,
∴,故②正确;
③在中,在中,
∴,故③正确;
④无法证明,故④错误;
∵ BDE和中,
∴,
∵,
∴ BDE与的面积之比不等于与的长度之比,故⑤错误;
综上分析可知:正确的有①②③.
故答案为:①②③.
1.(1)证明:∵是的垂直平分线,
∴,
∵,,
∴平分;
(2)解:∵,
∴,
∵是的垂直平分线,
∴,
∴,
∴,
∴,,
∴,
∴.
2.(1)证明:∵是的垂直平分线,
∴,
∴.
∵,,
∴,
∴,
∴平分.
(2)解:∵平分,,,
∴.
∵,,
∴.
∵,,
∴.
3.D
【知识点】全等的性质和HL综合(HL)、角平分线的性质定理、线段垂直平分线的性质、含30度角的直角三角形
【分析】由角平分线的性质可知①正确;②由题意可知,故此可知,,从而可证明②正确;连接,然后证明,从而得到,从而可证明③④.
【详解】解:如图所示:连接.
①∵平分,,,
∴,∴①正确.
②∵,平分,
∴,
∵,,
∴,
∵,,
∴,,
∴,∴②正确.
∵是的垂直平分线,
∴,
在和中,
,
∴,
∴,
∴,
又∵,,
∴,故③④正确.
故选:D.
1.C
【知识点】等边对等角、根据旋转的性质求解
【分析】本题考查的是旋转的性质,等腰三角形的性质,掌握“旋转前后的对应角相等与等边对等角”是解本题的关键.先由旋转的性质证明,,再利用等边对等角证明,从而可得答案.
【详解】解:将绕点逆时针旋转得到,点在上,
,,
,
,
,,
,
故选:C.
2.已知:如图,在 ABC中,,,平分和交,于点F,E,
求证:
证明:∵,
∴,
又∵,平分和,
∴,,
∴,
又∵,
∴,
∴.
3.(1)解:∵,,
∴,
∴,
∴,
∵,
∴;
(2)证明:,
,
.
在和中.
,
;
(3).理由如下:
由(2)知,
.
,
.
,
.
为等边三角形,
,
,
,
.
1.(1)证明:∵ ABC是等边三角形,
∴,
在与 CBF中,
∴,
∴;
(2)解:∵,
∴,
∵,即,
∴,
∴在中, ,
∵,
∴.
2.(1)证明:∵ ABD, EBC是等边三角形,
∴,
∴
∴
∴;
(2)∵ ABC是直角三角形,为直角边,
∴
∵ BEC是等边三角形,则,
∴,
由(1)可得
∴
∵是等边三角形,
∴
∴
∴
∴
∴垂直平分
∴.
3.(1)∵ ABC是等边三角形,
,
在和中,
,
,
,
,
故答案为:,;
(2)证明:由(1)可知,,
,
,
∴是等边三角形,
,
∵ ABC是等边三角形,
,
,
,
即,
,
,
,
,
平分.
1.D
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、含30度角的直角三角形
【分析】本题考查了全等三角形的判定和性质,直角三角形的性质,由“”可证,可得,由直角三角形的性质可得,,由线段的数量关系可求解,添加恰当辅助线构造全等三角形是解题的关键.
【详解】解:如图,过点作于,
,,,
,
在和中,
,
,
,
,,,
,
,,
,
,
,
,
,
故选:D.
2.A
【知识点】含30度角的直角三角形、等边三角形的性质
【分析】本题考查等边三角形的性质,掌握等边三角形的性质和含角的直角三角形的性质是解题的关键.
由等边三角形的性质及中点的定义得,,再根据直角三角形两锐角互余得,最后根据含角的直角三角形的性质即可得出答案.
【详解】解:∵ ABC是等边三角形,点是的中点,
∴,,
∵,,
∴,
∴,
∴,
∴,
∴
故选:A.
3.B
【知识点】全等的性质和ASA(AAS)综合(ASA或者AAS)、含30度角的直角三角形、等边三角形的性质
【分析】过点D作,交于F,先证 CDF是等边三角形,再证 PDF≌ PEB,得,设,则,最后根据在直角三角形中,的角所对的边是斜边的一半,计算,即可.
【详解】解:如下图,过点D作,交于F,
是等边三角形,
,
,
,
是等边三角形,
,
点P为中点,
,
在和中,
,
,
,
,
,
,
,
设,则,
,
解得:,
,
故选:B.
同课章节目录
