人教B版高中数学必修第一册第二章等式与不等式2.2.1不等式及其性质教学课件(共35张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册第二章等式与不等式2.2.1不等式及其性质教学课件(共35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 16:47:04 | ||
图片预览











文档简介
(共35张PPT)
2.2 不等式
2.2.1 不等式及其性质
第2章 等式与不等式
问题引入
新知探索
怎样理解两个实数之间的大小呢?
新知探索
新知探索
新知探索
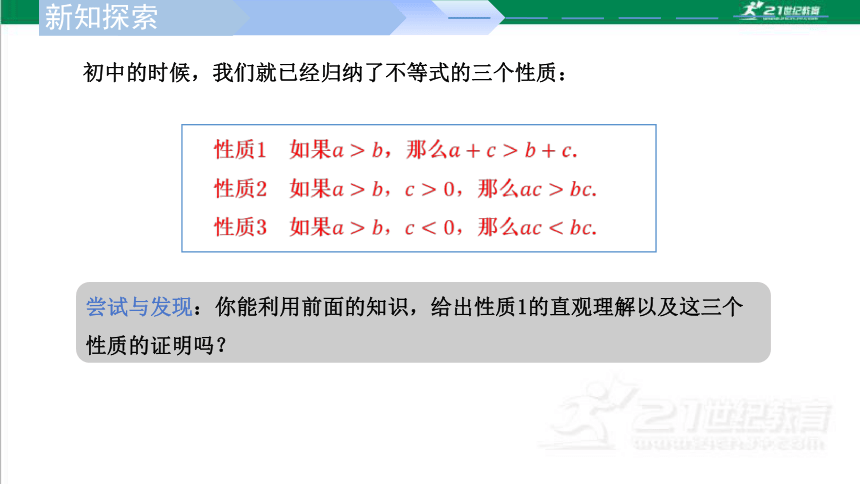
初中的时候,我们就已经归纳了不等式的三个性质:
尝试与发现:你能利用前面的知识,给出性质1的直观理解以及这三个性质的证明吗?
新知探索
新知探索
新知探索
充要
充要
充要
在不等式的证明与求解中,我们还经常用到以下不等式的性质.
新知探索
新知探索
另外,值得注意的是,上述不等式性质对任意满足条件的实数都成立,因此我们可以用任意满足条件的式子去代替其中的字母.
例题
例1的证明中用了配方法,这种方法经常用于式子变形,同学们应熟练掌握.
新知探索
需要注意的是,前面我们证明不等式性质和解答例1的方法,其实质都是通过比较两式之差的符号来判断两式的大小,这种方法通常称为作差法.在证明不等式时,当然也可以直接利用已经证明过的不等式性质等.从已知条件出发,综合利用各种结果,经过逐步推导最后得到结论的方法,在数学中通常称为综合法.下面用综合法来得出几个常用的不等式性质的推论.
推论1表明,不等式中的任意一项都可以把它的符号变成相反的符号后,从不等式的一边移到另一边.推论1通常称为不等式的移向法则.
新知探索
新知探索
很明显,这个推论也可以推广为更一般的结论:
几个两边都是正数的同向不等式的两边分别相乘,所得到的不等式与原不等式同向.
新知探索
这个结论的证明只要多次使用推论3的结论即可.
新知探索
可以看出,推论5中证明方法的实质是:首先假设结论的否定成立,然后由此进行推理得到矛盾,最后得出假设不成立.这种得到数学结论的方法通常称为反证法,反证法是一种间接证明的方法.
尝试与发现:证明推论5中不等式得方法具有什么特征?
例题
例题
新知探索
新知探索
例题
练习
题型一:用不等式(组表示不等关系)
练习
方法技巧:
1.用不等式(组)表示不等关系的步骤:
(1)审清题意,明确条件中的不等关系的个数;
(2)适当设未知数表示变量;
(3)用不等式表示每一个不等关系,并写成不等式组的形式.
2.用不等式表示不等关系的注意点
(1)利用不等式表示不等关系时,应注意必须是具有相同性质,可以比较大小的两个量才可用,没有可比性的两个量之间不能用不等式来表示.
(2)在用不等式表示实际问题时,一定要注意单位统一.
练习
练习
题型二:比较实数(式子)的大小
练习
方法技巧:
比较两个实数(代数式)大小的步骤:
(1)作差.对要比较大小的两个实数(或式子)作差;
(2)变形.对差进行变形;
(3)判断差的符号.结合变形的结果及题设条件判断差的符号;
(4)得出结论.
上述步骤可概括为“三步一结论”,这里的“判断符号”是目的,“变形”是关键.在变形中,一般变得越彻底,越有利于下一步的判断.其中变形的技巧较多,常见的有因式分解法、配方法、有理化法等.
练习
练习
练习
题型三:不等式性质的大小应用
角度(一) 判断命题的真假
练习
角度(二) 证明不等式
练习
角度(三) 求取值范围
练习
方法技巧:
利用不等式判断正误的2种方法:
(1)直接法:对于说法正确的,要利用不等式的相关性质证明;对于说法错误的,只需举出一个反例即可.
(2)特殊值法:注意取值一定要遵循三个原则:一是满足题设条件;二是取值要简单,便于验证计算;三是所取的值要有代表性.
练习
方法技巧:
(1)利用不等式的性质及其推论可以证明一些不等式,一定要在理解的基础上,记准、记熟不等式的性质及其推论,并注意在解题中灵活准确地加以应用.
(2)利用不等式的性质进行证明时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步证明,更不能随意构造性质与法则.
方法一(性质法)简单快捷,但思路不易发现;
方法二(作差法)思路简单,但通分较麻烦;
方法三(作商法)首先需要判断两个式子的符号,然后再判断其比值与1的大小关系,证明步骤较复杂.
课堂小结&作业
2.2 不等式
2.2.1 不等式及其性质
第2章 等式与不等式
问题引入
新知探索
怎样理解两个实数之间的大小呢?
新知探索
新知探索
新知探索
初中的时候,我们就已经归纳了不等式的三个性质:
尝试与发现:你能利用前面的知识,给出性质1的直观理解以及这三个性质的证明吗?
新知探索
新知探索
新知探索
充要
充要
充要
在不等式的证明与求解中,我们还经常用到以下不等式的性质.
新知探索
新知探索
另外,值得注意的是,上述不等式性质对任意满足条件的实数都成立,因此我们可以用任意满足条件的式子去代替其中的字母.
例题
例1的证明中用了配方法,这种方法经常用于式子变形,同学们应熟练掌握.
新知探索
需要注意的是,前面我们证明不等式性质和解答例1的方法,其实质都是通过比较两式之差的符号来判断两式的大小,这种方法通常称为作差法.在证明不等式时,当然也可以直接利用已经证明过的不等式性质等.从已知条件出发,综合利用各种结果,经过逐步推导最后得到结论的方法,在数学中通常称为综合法.下面用综合法来得出几个常用的不等式性质的推论.
推论1表明,不等式中的任意一项都可以把它的符号变成相反的符号后,从不等式的一边移到另一边.推论1通常称为不等式的移向法则.
新知探索
新知探索
很明显,这个推论也可以推广为更一般的结论:
几个两边都是正数的同向不等式的两边分别相乘,所得到的不等式与原不等式同向.
新知探索
这个结论的证明只要多次使用推论3的结论即可.
新知探索
可以看出,推论5中证明方法的实质是:首先假设结论的否定成立,然后由此进行推理得到矛盾,最后得出假设不成立.这种得到数学结论的方法通常称为反证法,反证法是一种间接证明的方法.
尝试与发现:证明推论5中不等式得方法具有什么特征?
例题
例题
新知探索
新知探索
例题
练习
题型一:用不等式(组表示不等关系)
练习
方法技巧:
1.用不等式(组)表示不等关系的步骤:
(1)审清题意,明确条件中的不等关系的个数;
(2)适当设未知数表示变量;
(3)用不等式表示每一个不等关系,并写成不等式组的形式.
2.用不等式表示不等关系的注意点
(1)利用不等式表示不等关系时,应注意必须是具有相同性质,可以比较大小的两个量才可用,没有可比性的两个量之间不能用不等式来表示.
(2)在用不等式表示实际问题时,一定要注意单位统一.
练习
练习
题型二:比较实数(式子)的大小
练习
方法技巧:
比较两个实数(代数式)大小的步骤:
(1)作差.对要比较大小的两个实数(或式子)作差;
(2)变形.对差进行变形;
(3)判断差的符号.结合变形的结果及题设条件判断差的符号;
(4)得出结论.
上述步骤可概括为“三步一结论”,这里的“判断符号”是目的,“变形”是关键.在变形中,一般变得越彻底,越有利于下一步的判断.其中变形的技巧较多,常见的有因式分解法、配方法、有理化法等.
练习
练习
练习
题型三:不等式性质的大小应用
角度(一) 判断命题的真假
练习
角度(二) 证明不等式
练习
角度(三) 求取值范围
练习
方法技巧:
利用不等式判断正误的2种方法:
(1)直接法:对于说法正确的,要利用不等式的相关性质证明;对于说法错误的,只需举出一个反例即可.
(2)特殊值法:注意取值一定要遵循三个原则:一是满足题设条件;二是取值要简单,便于验证计算;三是所取的值要有代表性.
练习
方法技巧:
(1)利用不等式的性质及其推论可以证明一些不等式,一定要在理解的基础上,记准、记熟不等式的性质及其推论,并注意在解题中灵活准确地加以应用.
(2)利用不等式的性质进行证明时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步证明,更不能随意构造性质与法则.
方法一(性质法)简单快捷,但思路不易发现;
方法二(作差法)思路简单,但通分较麻烦;
方法三(作商法)首先需要判断两个式子的符号,然后再判断其比值与1的大小关系,证明步骤较复杂.
课堂小结&作业
