人教B版高中数学必修第一册第三章函数3.1.3函数的奇偶性教学课件(共34张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册第三章函数3.1.3函数的奇偶性教学课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 16:49:43 | ||
图片预览










文档简介
(共34张PPT)
3.1 函数的概念及性质
3.1.3 函数的奇偶性
第3章 函数
复习引入
尝试与发现:填写下表,观察指定函数的自变量互为相反数时,函数值之间具有什么关系,并分别说出函数图象应具有的特征.
新知探索
新知探索
新知探索
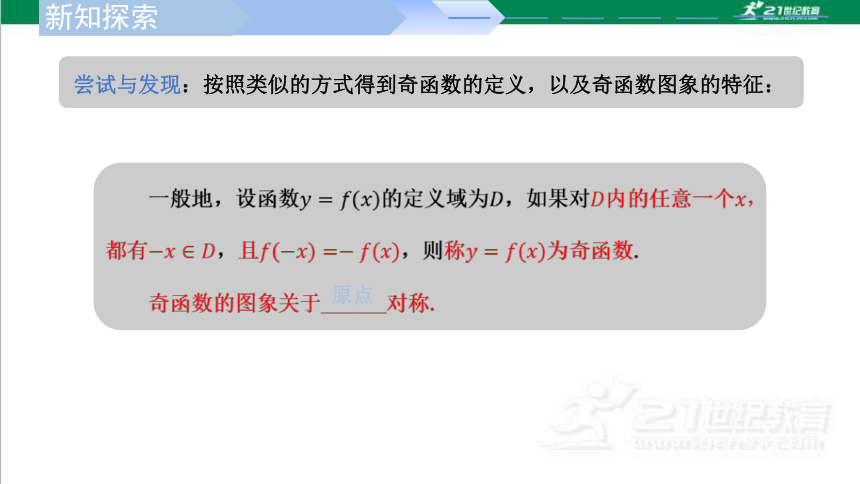
尝试与发现:按照类似的方式得到奇函数的定义,以及奇函数图象的特征:
原点
新知探索
例题
奇
偶
例题
例题
新知探索
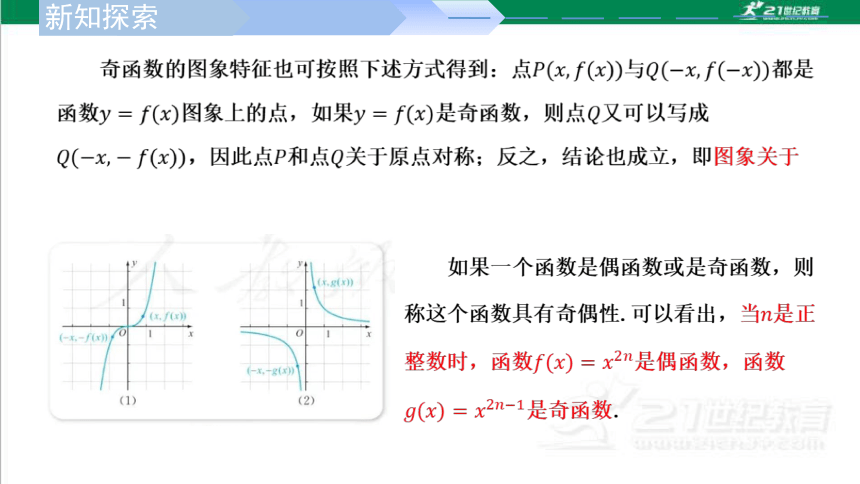
因为函数的奇偶性描述了函数图象具有的对称性,所以利用函数的奇偶性能简化函数性质的研究.如果知道一个函数是奇函数或是偶函数,那么其定义域能分成关于原点对称的两部分,得出函数在其中一部分上的性质和图象,就可得出这个函数在其中一部分上的性质和图象,就可得出这个函数在另一部分上的性质和图象.
例题
新知探索
例题
例题
例题
利用研究奇偶函数的类似方法还可以研究更一般的函数图象的对称性.
例题
例题
新知探索
练习
题型一:函数奇偶性的判断
练习
练习
练习
题型二:利用函数奇偶性求参数
练习
练习
练习
题型三:利用函数奇偶性求分段函数的解析式
练习
练习
练习
题型四:比较大小(奇偶性与单调性的综合)
练习
方法技巧:
综合利用函数奇偶性和单调性比较大小
(1)若自变量在同一区间内,直接利用函数的单调性比较大小;
(2)若自变量不在同一区间内,需利用函数的奇偶性把自变量转化的同一区间内,再利用单调性比较大小.
练习
练习
题型五:解不等式问题(奇偶性与单调性的综合)
练习
方法技巧:
利用函数的奇偶性与单调性解不等式问题
(1)注意“含参数的定义域”要在函数的定义域内,进而列出不等式;
(2)根据函数的单调性,列出关于两个“含参定义域”的大小不等式;
(3)联立不等式,求出参数即不等式的解集.
练习
课堂小结&作业
3.1 函数的概念及性质
3.1.3 函数的奇偶性
第3章 函数
复习引入
尝试与发现:填写下表,观察指定函数的自变量互为相反数时,函数值之间具有什么关系,并分别说出函数图象应具有的特征.
新知探索
新知探索
新知探索
尝试与发现:按照类似的方式得到奇函数的定义,以及奇函数图象的特征:
原点
新知探索
例题
奇
偶
例题
例题
新知探索
因为函数的奇偶性描述了函数图象具有的对称性,所以利用函数的奇偶性能简化函数性质的研究.如果知道一个函数是奇函数或是偶函数,那么其定义域能分成关于原点对称的两部分,得出函数在其中一部分上的性质和图象,就可得出这个函数在其中一部分上的性质和图象,就可得出这个函数在另一部分上的性质和图象.
例题
新知探索
例题
例题
例题
利用研究奇偶函数的类似方法还可以研究更一般的函数图象的对称性.
例题
例题
新知探索
练习
题型一:函数奇偶性的判断
练习
练习
练习
题型二:利用函数奇偶性求参数
练习
练习
练习
题型三:利用函数奇偶性求分段函数的解析式
练习
练习
练习
题型四:比较大小(奇偶性与单调性的综合)
练习
方法技巧:
综合利用函数奇偶性和单调性比较大小
(1)若自变量在同一区间内,直接利用函数的单调性比较大小;
(2)若自变量不在同一区间内,需利用函数的奇偶性把自变量转化的同一区间内,再利用单调性比较大小.
练习
练习
题型五:解不等式问题(奇偶性与单调性的综合)
练习
方法技巧:
利用函数的奇偶性与单调性解不等式问题
(1)注意“含参数的定义域”要在函数的定义域内,进而列出不等式;
(2)根据函数的单调性,列出关于两个“含参定义域”的大小不等式;
(3)联立不等式,求出参数即不等式的解集.
练习
课堂小结&作业
