人教B版高中数学必修第一册第三章函数3.1.2函数的单调性教学课件(共33张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册第三章函数3.1.2函数的单调性教学课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
3.1 函数的概念及性质
3.1.2 函数的单调性
第3章 函数
问题引入
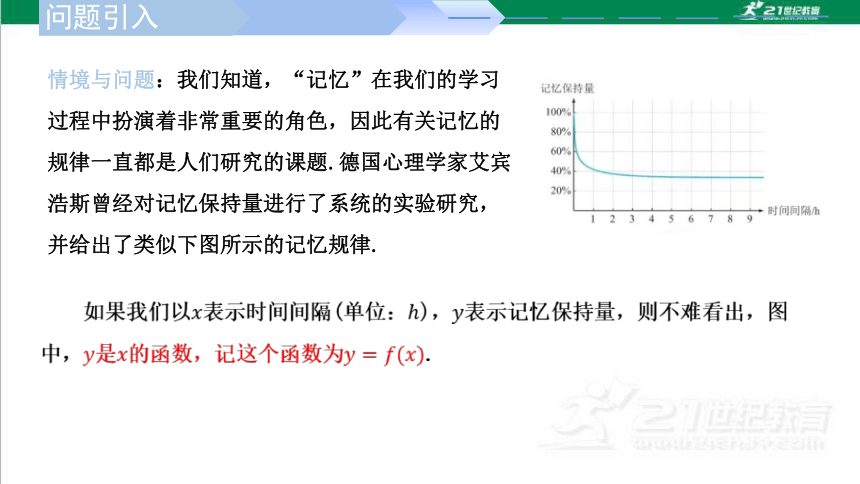
情境与问题:我们知道,“记忆”在我们的学习过程中扮演着非常重要的角色,因此有关记忆的规律一直都是人们研究的课题.德国心理学家艾宾浩斯曾经对记忆保持量进行了系统的实验研究,并给出了类似下图所示的记忆规律.
新知探索
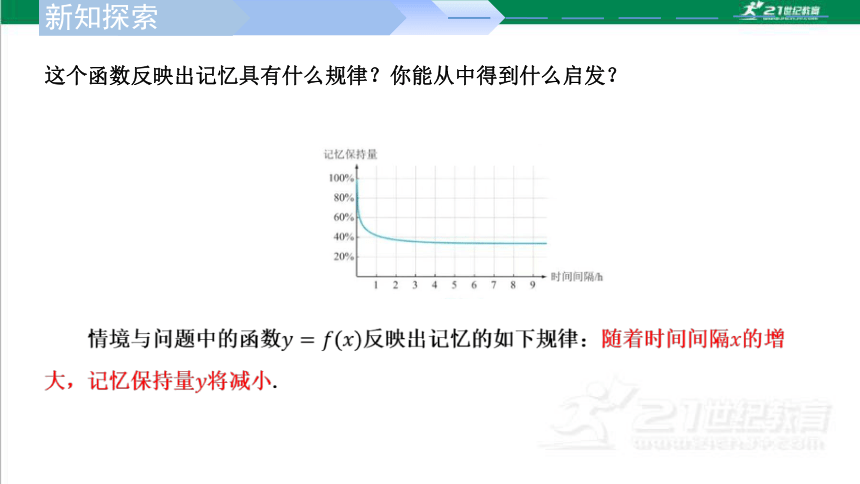
这个函数反映出记忆具有什么规律?你能从中得到什么启发?
新知探索
给定一个函数,人们有时候关心的是,函数值会随着自变量增大而怎样变化,类似的内容我们在初中曾经接触过.
新知探索
新知探索
新知探索
增
减
增
由尝试与发现可知,从函数的图象能方便地看出函数的单调性.但一般情况下,得到函数的图象并不容易,而且手工作出的图象往往都不精确,因此我们要探讨怎样从函数的解析式来证明函数的单调性.这可以利用函数单调性的定义和不等式的证明方法.
例题
新知探索
不难看出,如果函数有最值而且函数的单调性容易求出,则可利用函数的单调性求出函数的最值点和最值.
例题
所以这个函数是_____函数.
从而这个函数的最小值为_____,最大值为______.
增
2
23
新知探索
新知探索
不难看出,平面直角坐标系中的三个点共线,当且仅当其中任意两点确定的直线的斜率都相等或不存在.下面我们用直线的斜率来研究函数的单调性.
由函数的定义可知,任何一个函数图象上的两个点,它们所确定的直线的斜率一定存在.
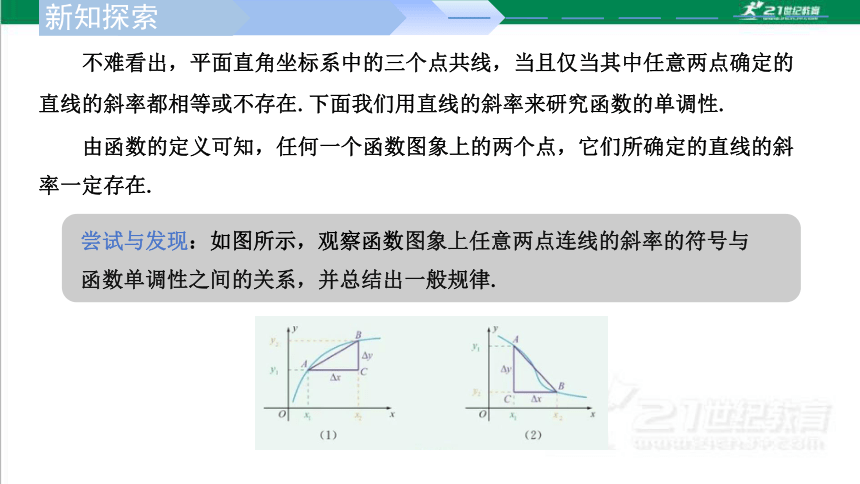
尝试与发现:如图所示,观察函数图象上任意两点连线的斜率的符号与函数单调性之间的关系,并总结出一般规律.
新知探索
可以看出,函数递增的充要条件是其图象上任意两点的斜率都大于0,函数递减的充要条件是其图象上任意两点连线的斜率都小于0.
新知探索
利用上述结论,我们可以证明一个函数的单调性.
减
例题
例题
新知探索
新知探索
新知探索
例题
例题
新知探索
增
减
小
练习
题型一:判断(证明)函数的单调性)
练习
答案:CD.
练习
题型二:图象法求函数的单调区间
解:函数图象如图所示:
练习
(解答思路同例2)
图象法求函数单调区间的步骤:
(1)作图;
(2)结论:上升图象对应单调递增区间,下降图象对应单调递减区间.
练习
题型三:函数单调性的应用
练习
练习
练习
题型四:图象法求函数的最值)
练习
练习
答案:D
课堂小结&作业
3.1 函数的概念及性质
3.1.2 函数的单调性
第3章 函数
问题引入
情境与问题:我们知道,“记忆”在我们的学习过程中扮演着非常重要的角色,因此有关记忆的规律一直都是人们研究的课题.德国心理学家艾宾浩斯曾经对记忆保持量进行了系统的实验研究,并给出了类似下图所示的记忆规律.
新知探索
这个函数反映出记忆具有什么规律?你能从中得到什么启发?
新知探索
给定一个函数,人们有时候关心的是,函数值会随着自变量增大而怎样变化,类似的内容我们在初中曾经接触过.
新知探索
新知探索
新知探索
增
减
增
由尝试与发现可知,从函数的图象能方便地看出函数的单调性.但一般情况下,得到函数的图象并不容易,而且手工作出的图象往往都不精确,因此我们要探讨怎样从函数的解析式来证明函数的单调性.这可以利用函数单调性的定义和不等式的证明方法.
例题
新知探索
不难看出,如果函数有最值而且函数的单调性容易求出,则可利用函数的单调性求出函数的最值点和最值.
例题
所以这个函数是_____函数.
从而这个函数的最小值为_____,最大值为______.
增
2
23
新知探索
新知探索
不难看出,平面直角坐标系中的三个点共线,当且仅当其中任意两点确定的直线的斜率都相等或不存在.下面我们用直线的斜率来研究函数的单调性.
由函数的定义可知,任何一个函数图象上的两个点,它们所确定的直线的斜率一定存在.
尝试与发现:如图所示,观察函数图象上任意两点连线的斜率的符号与函数单调性之间的关系,并总结出一般规律.
新知探索
可以看出,函数递增的充要条件是其图象上任意两点的斜率都大于0,函数递减的充要条件是其图象上任意两点连线的斜率都小于0.
新知探索
利用上述结论,我们可以证明一个函数的单调性.
减
例题
例题
新知探索
新知探索
新知探索
例题
例题
新知探索
增
减
小
练习
题型一:判断(证明)函数的单调性)
练习
答案:CD.
练习
题型二:图象法求函数的单调区间
解:函数图象如图所示:
练习
(解答思路同例2)
图象法求函数单调区间的步骤:
(1)作图;
(2)结论:上升图象对应单调递增区间,下降图象对应单调递减区间.
练习
题型三:函数单调性的应用
练习
练习
练习
题型四:图象法求函数的最值)
练习
练习
答案:D
课堂小结&作业
