人教B版高中数学必修第一册第一章集合与常用逻辑用语1.1.3集合的基本运算教学课件(共23张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册第一章集合与常用逻辑用语1.1.3集合的基本运算教学课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 16:50:28 | ||
图片预览








文档简介
(共23张PPT)
第1章 集合与常用逻辑用语
1.1.3 集合的基本运算
1.理解并集、交集、补集的概念.(重点)
2.会求已知集合的并集、交集和补集.(重点)
3.能正确应用并集、交集和补集解决实际问题.(难点)
学习目标
新知探究1——交集
学校高一年级准备成立一个科学兴趣小组,招募成员时要求同时满足:
(1)中考的物理成绩不低于80分;
(2)中考的数学成绩不低于70分
如果满足条件(1)的同学组成的集合记为P,满足条件(2)的同学组成的集合
记为 M,而能成为科学兴趣小组成员的同学组成的集合记为S,那么这三个集合之
间有什么联系呢
可以看出,集合S中的元素既属于集合P,又属于集合M.
1.交集
典例精讲
例1 求下列每对集合的交集:
(1)A={1,-3},B={-1,-3};
(2)C={1,3,5,7},D={2,4,6,8};
(3)E=(1,3],F=[-2,2).
例2 已知 A={x|x 是菱形},B={x|x是矩形},求 A∩B.
【解析】A∩B={x|x 是菱形}∩{x|x 是矩形}={x|x 是正方形}.
我们经常使用的“且”可以借助集合的交集来理解,例如,平面直角坐标系中的点(x,y)在第一象限的条件是:横坐标大于0且纵坐标大于0,用集合的语言可以表示为
{ (x,y) | x>0 }∩{ (x,y) | y>0 }={ (x,y) | x>0,y>0 },
也就是说,为了保证点(x,y)在第一象限,条件坐标大于0与纵坐标大于0要同时成立.
新知探究1——并集
某班班主任准备召开一个意见征求会,要求所有上一次考试中语文成绩低于70
分或英语成绩低于 70分的同学参加。如果记语文成绩低于70分的所有同学组成的集
合为 M,英语成绩低于 70分的所有同学组成的集合为 N,需要去参加意见征求会的
同学组成的集合为P,那么这三个集合之间有什么联系呢
可以看出,集合P中的元素,要么属于集合M,要么属于集合N.
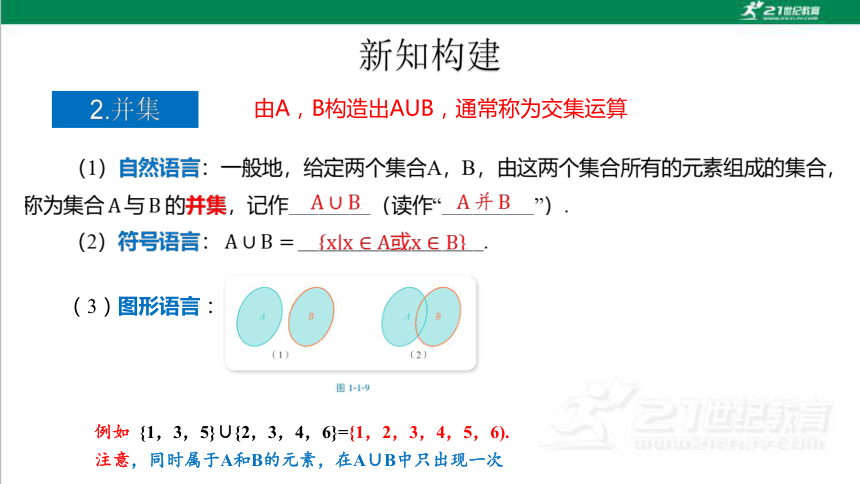
2.并集
由A,B构造出AUB,通常称为交集运算
例如 {1,3,5}∪{2,3,4,6}={1,2,3,4,5,6).
注意,同时属于A和B的元素,在A∪B中只出现一次
尝试练习
典例精讲
例3.已知区间A=(-3,1),B=[-2,3],求A∩B,A∪B.
【解析】在数轴上表示出A和B,如图1-1-10所示,
由图可知:A∩B= ____ ,AUB= ____
我们经常使用的“或”可以借助集合的并集来理解.
例如,x≥0的含义是x>0或x=0,这可以用集合语言表示为
{ x | x ≥ 0 }={ x | x>0 或 x=0 } = { x | x>0 } ∪ { x | x=0 },
也就是说,为了保证x≥0,条件x>0与x=0只要有一个成立即可.
[-2,1)
(-3,3]
探索与研究
(1)设有限集M 所含元素的个数用 card(M)表示,并规定 card( )=0.已知
A={x|x是外语兴趣小组的成员},B={x|x是数学兴趣小组的成员),且
card(A)=20,card(B)=8,card(A∩B)=4,你能求出 card(AUB)吗
(2)设A,B为两个有限集,讨论 card(A),card(B),card(A∩B), card(AUB)之间的关系.
【解析】(1) card(AUB)=20+8-4=24
(2) card(AUB)=card(A)+card(B)-card(A∩B)
新知探究3——补集
学
科
网
如果学校里所有同学组成的集合记为S,所有男同学组成的集合记为M,所女同学组成的集合记为F,那么:
(1)这三个集合之间有什么联系
(2)如果x∈S且x M,你能得到什么结论
可以看出,集合M和集合F都是集合S的子集,而且
如果x∈S且x M,则一定有x∈F.
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用U表示.
如果集合A是全集U的一个子集,则由U中不属于A的所有元素组成的集合,称为A在U中的补集,记作: ,读作:“A在U中的补集”.
3.补集
图形语言:
补集的运算性质:
典例精讲
【解析】在数轴上表示出A和B,如图1-1-12所示
探索与研究
给定三个集合A,B,C,式子(A∪B)∩C的意义是什么 (A∩C)∪(B∩C)呢
作维恩图研究这两个式子之间的关系,并研究(A∩B)∪C和(A∪C)∩(B∪C)之间的关系.
【解析】(A∪B)∩C的意义是:由集合A或B中的元素,同时又在集合C中元素构成的集合;
(A∩C)∪(B∩C)的意义是:由集合A与C的公共元素,与集合B与C的公共元素构成的集合.
U
A
B
C
①
②
③
(A∪B)∩C表示图中区域为:①②③
(A∩C)∪(B∩C)表示图中区域为:①②③
(A∩B)∪C表示图中区域为:C+④
(A∪C)∩(B∪C)表示图中区域为:C+④
④
如图:
∴(A∪B)∩C=(A∩C)∪(B∩C)
(A∩B)∪C=(A∪C)∩(B∪C)
典例精讲
(重难点题型)由并集、交集的定义和性质求参数的范围
例6 已知集合A={x|-3<x≤4},集合B={x|k+1≤x≤2k-1},且A∪B=A,试求k的取值范围.
【解析】∵A∪B=A,∴B A,
①当B= 时,k+1>2k-1,∴k<2.
②当B≠ ,则根据题意如图所示:
根据数轴可得解得.
综合①②可得k的取值范围为
解决问题
小组研讨
解决问题
小组研讨
1.求两个集合的并集方法:
1.离散型集合的并集,多借助定义或Venn图求解.
1.对于元素个数有限的集合,逐个挑出两个集合的公共元素即可;
2.对于元素是连续实数的集合,一般借助数轴求交集,在数轴上的相应图形所覆盖的公共范围,要注意端点值的取舍.
2.求两个集合的交集方法:
3.补集的求解步骤及方法:
1.步骤:①确定全集,在进行补集的简单运算时,应首先明确全集;
②紧扣定义求解补集.
集合的基本运算
课堂练习A
A∩B={b,d}, A∪B={a,b,c,d,e,f}
A∩B=(2,+∞), A∪B=(0,+∞)
A∩B表示既选羽毛球又选乒乓球的 同学的集合 A∪B表示所有选羽毛球或选乒乓球的同学的集合
课堂练习B
总成立. A∩B= 和A∩B≠ 两种情况都成立
(1)a=3
(2)∵2≤a<4 ,∴a的取值范围是[2,4)
第1章 集合与常用逻辑用语
1.1.3 集合的基本运算
1.理解并集、交集、补集的概念.(重点)
2.会求已知集合的并集、交集和补集.(重点)
3.能正确应用并集、交集和补集解决实际问题.(难点)
学习目标
新知探究1——交集
学校高一年级准备成立一个科学兴趣小组,招募成员时要求同时满足:
(1)中考的物理成绩不低于80分;
(2)中考的数学成绩不低于70分
如果满足条件(1)的同学组成的集合记为P,满足条件(2)的同学组成的集合
记为 M,而能成为科学兴趣小组成员的同学组成的集合记为S,那么这三个集合之
间有什么联系呢
可以看出,集合S中的元素既属于集合P,又属于集合M.
1.交集
典例精讲
例1 求下列每对集合的交集:
(1)A={1,-3},B={-1,-3};
(2)C={1,3,5,7},D={2,4,6,8};
(3)E=(1,3],F=[-2,2).
例2 已知 A={x|x 是菱形},B={x|x是矩形},求 A∩B.
【解析】A∩B={x|x 是菱形}∩{x|x 是矩形}={x|x 是正方形}.
我们经常使用的“且”可以借助集合的交集来理解,例如,平面直角坐标系中的点(x,y)在第一象限的条件是:横坐标大于0且纵坐标大于0,用集合的语言可以表示为
{ (x,y) | x>0 }∩{ (x,y) | y>0 }={ (x,y) | x>0,y>0 },
也就是说,为了保证点(x,y)在第一象限,条件坐标大于0与纵坐标大于0要同时成立.
新知探究1——并集
某班班主任准备召开一个意见征求会,要求所有上一次考试中语文成绩低于70
分或英语成绩低于 70分的同学参加。如果记语文成绩低于70分的所有同学组成的集
合为 M,英语成绩低于 70分的所有同学组成的集合为 N,需要去参加意见征求会的
同学组成的集合为P,那么这三个集合之间有什么联系呢
可以看出,集合P中的元素,要么属于集合M,要么属于集合N.
2.并集
由A,B构造出AUB,通常称为交集运算
例如 {1,3,5}∪{2,3,4,6}={1,2,3,4,5,6).
注意,同时属于A和B的元素,在A∪B中只出现一次
尝试练习
典例精讲
例3.已知区间A=(-3,1),B=[-2,3],求A∩B,A∪B.
【解析】在数轴上表示出A和B,如图1-1-10所示,
由图可知:A∩B= ____ ,AUB= ____
我们经常使用的“或”可以借助集合的并集来理解.
例如,x≥0的含义是x>0或x=0,这可以用集合语言表示为
{ x | x ≥ 0 }={ x | x>0 或 x=0 } = { x | x>0 } ∪ { x | x=0 },
也就是说,为了保证x≥0,条件x>0与x=0只要有一个成立即可.
[-2,1)
(-3,3]
探索与研究
(1)设有限集M 所含元素的个数用 card(M)表示,并规定 card( )=0.已知
A={x|x是外语兴趣小组的成员},B={x|x是数学兴趣小组的成员),且
card(A)=20,card(B)=8,card(A∩B)=4,你能求出 card(AUB)吗
(2)设A,B为两个有限集,讨论 card(A),card(B),card(A∩B), card(AUB)之间的关系.
【解析】(1) card(AUB)=20+8-4=24
(2) card(AUB)=card(A)+card(B)-card(A∩B)
新知探究3——补集
学
科
网
如果学校里所有同学组成的集合记为S,所有男同学组成的集合记为M,所女同学组成的集合记为F,那么:
(1)这三个集合之间有什么联系
(2)如果x∈S且x M,你能得到什么结论
可以看出,集合M和集合F都是集合S的子集,而且
如果x∈S且x M,则一定有x∈F.
在研究集合与集合之间的关系时,如果所要研究的集合都是某一给定集合的子集,那么称这个给定的集合为全集,全集通常用U表示.
如果集合A是全集U的一个子集,则由U中不属于A的所有元素组成的集合,称为A在U中的补集,记作: ,读作:“A在U中的补集”.
3.补集
图形语言:
补集的运算性质:
典例精讲
【解析】在数轴上表示出A和B,如图1-1-12所示
探索与研究
给定三个集合A,B,C,式子(A∪B)∩C的意义是什么 (A∩C)∪(B∩C)呢
作维恩图研究这两个式子之间的关系,并研究(A∩B)∪C和(A∪C)∩(B∪C)之间的关系.
【解析】(A∪B)∩C的意义是:由集合A或B中的元素,同时又在集合C中元素构成的集合;
(A∩C)∪(B∩C)的意义是:由集合A与C的公共元素,与集合B与C的公共元素构成的集合.
U
A
B
C
①
②
③
(A∪B)∩C表示图中区域为:①②③
(A∩C)∪(B∩C)表示图中区域为:①②③
(A∩B)∪C表示图中区域为:C+④
(A∪C)∩(B∪C)表示图中区域为:C+④
④
如图:
∴(A∪B)∩C=(A∩C)∪(B∩C)
(A∩B)∪C=(A∪C)∩(B∪C)
典例精讲
(重难点题型)由并集、交集的定义和性质求参数的范围
例6 已知集合A={x|-3<x≤4},集合B={x|k+1≤x≤2k-1},且A∪B=A,试求k的取值范围.
【解析】∵A∪B=A,∴B A,
①当B= 时,k+1>2k-1,∴k<2.
②当B≠ ,则根据题意如图所示:
根据数轴可得解得.
综合①②可得k的取值范围为
解决问题
小组研讨
解决问题
小组研讨
1.求两个集合的并集方法:
1.离散型集合的并集,多借助定义或Venn图求解.
1.对于元素个数有限的集合,逐个挑出两个集合的公共元素即可;
2.对于元素是连续实数的集合,一般借助数轴求交集,在数轴上的相应图形所覆盖的公共范围,要注意端点值的取舍.
2.求两个集合的交集方法:
3.补集的求解步骤及方法:
1.步骤:①确定全集,在进行补集的简单运算时,应首先明确全集;
②紧扣定义求解补集.
集合的基本运算
课堂练习A
A∩B={b,d}, A∪B={a,b,c,d,e,f}
A∩B=(2,+∞), A∪B=(0,+∞)
A∩B表示既选羽毛球又选乒乓球的 同学的集合 A∪B表示所有选羽毛球或选乒乓球的同学的集合
课堂练习B
总成立. A∩B= 和A∩B≠ 两种情况都成立
(1)a=3
(2)∵2≤a<4 ,∴a的取值范围是[2,4)
