3.4直线与圆的位置关系(4)学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 3.4直线与圆的位置关系(4)学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 166.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 00:00:00 | ||
图片预览

文档简介
3.4 直线与圆的位置关系(4)
【学习目标】
1.了解切线长的概念
2.理解切线长定理,熟练掌握它的应用
【学习重点】切线长定理及其应用
【学习难点】切线长定理的推导及其证明,用切线长定理解决实际问题
【学习过程】
复习引入
直线和圆的位置判定方法有几种?
新知探究
探究1.切线长定理
(1)在透明纸上画出⊙O,在⊙O上取一点A,过点A画出⊙O的切线,在过点A的切线上任取一点P。
(2)把你画出的图形沿直线PO对折,你发现点A关于PO的对称点B在⊙O上吗?由此你能发现哪些结论?与同学交流。
(3)能证明你的结论是正确的吗?
如图,已知P是⊙O外一点,PA 是⊙O的切线. 过切点A作PO的垂线,垂足为点C,交⊙O于点B,连接PB,OA,OB。
知识点1.切线长
经过圆外一点可以画圆的两条切线,这点与其中一个切点之间的 ,叫做这点到圆的切线长
知识点2.切线长定理
过圆外一点所画的圆的两条
【跟踪练习】
如图,P 是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA = 4 cm,PC = 2 cm . ∠APB=_________.(tan37°≈)
小结:切线长定理中的钻石模型
如图,PA,PB是⊙O的切线
(1)一条角平分线:OP平分∠APB和∠AOB
(2)两个等腰三角形:△AOB和△PAB
(3)两组相等的角:∠1=∠2=∠3=∠4,∠AOP=∠BOP
(4)两组相等的线段:AD=BD,PA=PB
(5)两组相等的弧:,
(6)三个垂直:OA⊥PA,OB⊥PB,OP⊥AB
(7)三组全等三角形:△OAP≌△OBP,△OAD≌△OBD,△ADP≌△BDP
典型例题
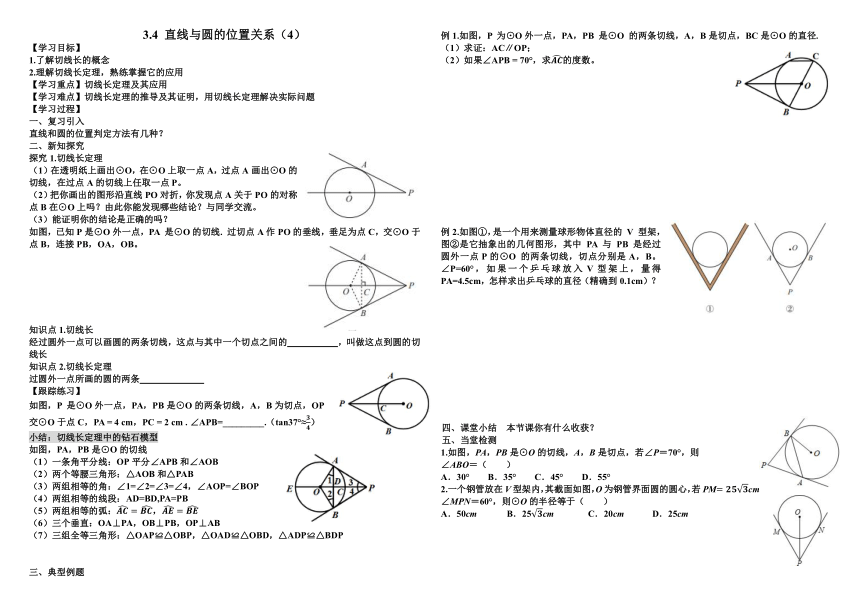
例1.如图,P 为⊙O外一点,PA,PB 是⊙O 的两条切线,A,B是切点,BC是⊙O的直径.
(1)求证:AC∥OP;
(2)如果∠APB = 70°,求的度数。
例2.如图①,是一个用来测量球形物体直径的 V 型架,图②是它抽象出的几何图形,其中 PA 与 PB 是经过圆外一点P的⊙O 的两条切线,切点分别是A,B。∠P=60°,如果一个乒乓球放入V型架上,量得PA=4.5cm,怎样求出乒乓球的直径(精确到0.1cm)?
四、课堂小结 本节课你有什么收获?
五、当堂检测
1.如图,PA,PB是⊙O的切线,A,B是切点,若∠P=70°,则
∠ABO=( )
A.30° B.35° C.45° D.55°
2.一个钢管放在V型架内,其截面如图,O为钢管界面圆的圆心,若PMcm,∠MPN=60°,则⊙O的半径等于( )
A.50cm B.25cm C.20cm D.25cm
六、课后分层作业
【基础闯关】
1.如图,PA、PB分别与⊙O相切于A、B两点,∠C=50°,则∠P=( )
A.50° B.100° C.130° D.80°
2.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
A.28° B.50° C.56° D.62°
3.如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm B.7cm
C.6cm D.随直线MN的变化而变化
4.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠BAC=25°,则∠P=( )度.
A.30 B.60 C.50 D.75
第1题 第2题 第3题 第4题
5.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是( )
A.3cm B.3 cm C.6cm D.6cm
6.已知:如图,PA,PB,DC分别切⊙O于A,B,E点,若PA=10cm,则△PCD的周长为 .
7.如图,PA、PB分别与⊙O相切于点A、B,∠P=70°,C为弧AB上一点,则∠ACB的度数为 .
【能力提升】
8.如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P.若四边形ABCD的周长为20,则AB+CD等于( )
A.5 B.8 C.10 D.12
第5题 第6题 第7题 第8题
9.矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为( )
A. B. C. D.
10.如图,已知PA、PB是⊙O的两条切线,点A、点B为切点,线段OP
交⊙O于点M.下列结论:①PA=PB; ②OP⊥AB;③四边形OAPB有外接圆;④点M是△AOP外接圆的圆心.其中正确的结论是 (填序号).
如图,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,
∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是 .
12.如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE= .
第9题 第10题 第11题 第12题
13.如图,△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)求CD的长.
【培优创新】
14.如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
【学习目标】
1.了解切线长的概念
2.理解切线长定理,熟练掌握它的应用
【学习重点】切线长定理及其应用
【学习难点】切线长定理的推导及其证明,用切线长定理解决实际问题
【学习过程】
复习引入
直线和圆的位置判定方法有几种?
新知探究
探究1.切线长定理
(1)在透明纸上画出⊙O,在⊙O上取一点A,过点A画出⊙O的切线,在过点A的切线上任取一点P。
(2)把你画出的图形沿直线PO对折,你发现点A关于PO的对称点B在⊙O上吗?由此你能发现哪些结论?与同学交流。
(3)能证明你的结论是正确的吗?
如图,已知P是⊙O外一点,PA 是⊙O的切线. 过切点A作PO的垂线,垂足为点C,交⊙O于点B,连接PB,OA,OB。
知识点1.切线长
经过圆外一点可以画圆的两条切线,这点与其中一个切点之间的 ,叫做这点到圆的切线长
知识点2.切线长定理
过圆外一点所画的圆的两条
【跟踪练习】
如图,P 是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA = 4 cm,PC = 2 cm . ∠APB=_________.(tan37°≈)
小结:切线长定理中的钻石模型
如图,PA,PB是⊙O的切线
(1)一条角平分线:OP平分∠APB和∠AOB
(2)两个等腰三角形:△AOB和△PAB
(3)两组相等的角:∠1=∠2=∠3=∠4,∠AOP=∠BOP
(4)两组相等的线段:AD=BD,PA=PB
(5)两组相等的弧:,
(6)三个垂直:OA⊥PA,OB⊥PB,OP⊥AB
(7)三组全等三角形:△OAP≌△OBP,△OAD≌△OBD,△ADP≌△BDP
典型例题
例1.如图,P 为⊙O外一点,PA,PB 是⊙O 的两条切线,A,B是切点,BC是⊙O的直径.
(1)求证:AC∥OP;
(2)如果∠APB = 70°,求的度数。
例2.如图①,是一个用来测量球形物体直径的 V 型架,图②是它抽象出的几何图形,其中 PA 与 PB 是经过圆外一点P的⊙O 的两条切线,切点分别是A,B。∠P=60°,如果一个乒乓球放入V型架上,量得PA=4.5cm,怎样求出乒乓球的直径(精确到0.1cm)?
四、课堂小结 本节课你有什么收获?
五、当堂检测
1.如图,PA,PB是⊙O的切线,A,B是切点,若∠P=70°,则
∠ABO=( )
A.30° B.35° C.45° D.55°
2.一个钢管放在V型架内,其截面如图,O为钢管界面圆的圆心,若PMcm,∠MPN=60°,则⊙O的半径等于( )
A.50cm B.25cm C.20cm D.25cm
六、课后分层作业
【基础闯关】
1.如图,PA、PB分别与⊙O相切于A、B两点,∠C=50°,则∠P=( )
A.50° B.100° C.130° D.80°
2.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB的度数为( )
A.28° B.50° C.56° D.62°
3.如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A.12cm B.7cm
C.6cm D.随直线MN的变化而变化
4.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠BAC=25°,则∠P=( )度.
A.30 B.60 C.50 D.75
第1题 第2题 第3题 第4题
5.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是( )
A.3cm B.3 cm C.6cm D.6cm
6.已知:如图,PA,PB,DC分别切⊙O于A,B,E点,若PA=10cm,则△PCD的周长为 .
7.如图,PA、PB分别与⊙O相切于点A、B,∠P=70°,C为弧AB上一点,则∠ACB的度数为 .
【能力提升】
8.如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别相切于点L、M、N、P.若四边形ABCD的周长为20,则AB+CD等于( )
A.5 B.8 C.10 D.12
第5题 第6题 第7题 第8题
9.矩形ABCD中,AB=4,AD=3,以AB为直径在矩形内作半圆.DE切⊙O于点E(如图),则tan∠CDF的值为( )
A. B. C. D.
10.如图,已知PA、PB是⊙O的两条切线,点A、点B为切点,线段OP
交⊙O于点M.下列结论:①PA=PB; ②OP⊥AB;③四边形OAPB有外接圆;④点M是△AOP外接圆的圆心.其中正确的结论是 (填序号).
如图,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,
∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是 .
12.如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE= .
第9题 第10题 第11题 第12题
13.如图,△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)求CD的长.
【培优创新】
14.如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
