3.7正多边形与圆 学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 3.7正多边形与圆 学案(无答案)2024-2025学年青岛版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 111.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 15:52:57 | ||
图片预览

文档简介
3.7 正多边形与圆
【学习目标】
1.了解正多边形的概念及正多边形与圆的关系
2.能运用正多边形的边长、半径、边心距等进行计算
【学习重点】正多边形的概念及正多边形与圆的关系
【学习难点】正多边形性质的应用
【学习过程】
一、复习引入
你还记得什么叫正多边形吗?说出你常见的几种正多边形。
二、新知探究
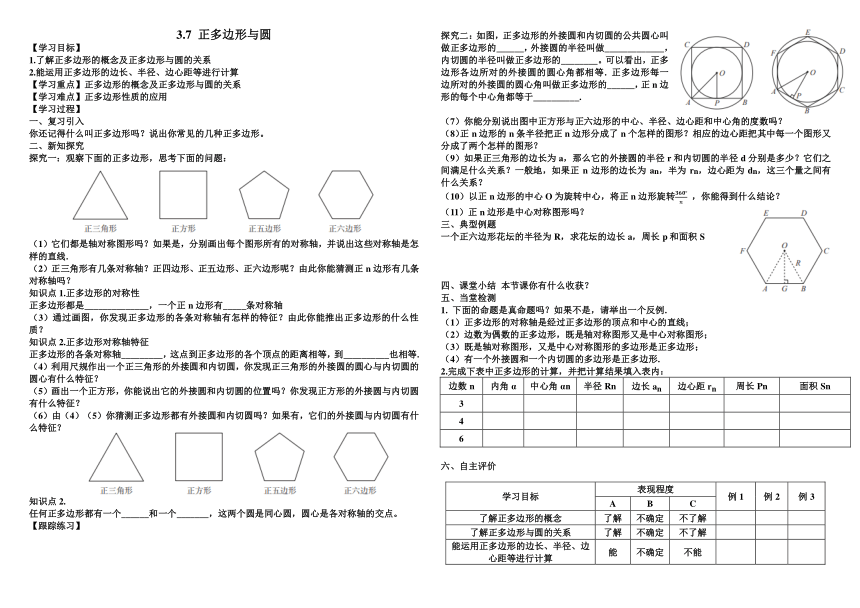
探究一:观察下面的正多边形,思考下面的问题:
(1)它们都是轴对称图形吗?如果是,分别画出每个图形所有的对称轴,并说出这些对称轴是怎样的直线.
(2)正三角形有几条对称轴?正四边形、正五边形、正六边形呢?由此你能猜测正n边形有几条对称轴吗?
知识点1.正多边形的对称性
正多边形都是______________,一个正n边形有_____条对称轴
(3)通过画图,你发现正多边形的各条对称轴有怎样的特征?由此你能推出正多边形的什么性质?
知识点2.正多边形对称轴特征
正多边形的各条对称轴_________,这点到正多边形的各个顶点的距离相等,到__________也相等.
(4)利用尺规作出一个正三角形的外接圆和内切圆,你发现正三角形的外接圆的圆心与内切圆的圆心有什么特征?
(5)画出一个正方形,你能说出它的外接圆和内切圆的位置吗?你发现正方形的外接圆与内切圆有什么特征?
(6)由(4)(5)你猜测正多边形都有外接圆和内切圆吗?如果有,它们的外接圆与内切圆有什么特征?
知识点2.
任何正多边形都有一个______和一个_______,这两个圆是同心圆,圆心是各对称轴的交点。
【跟踪练习】
探究二:如图,正多边形的外接圆和内切圆的公共圆心叫做正多边形的______,外接圆的半径叫做_____________,内切圆的半径叫做正多边形的________。可以看出,正多边形各边所对的外接圆的圆心角都相等. 正多边形每一边所对的外接圆的圆心角叫做正多边形的______,正n边形的每个中心角都等于__________.
(7)你能分别说出图中正方形与正六边形的中心、半径、边心距和中心角的度数吗?
(8)正n边形的n条半径把正n边形分成了n个怎样的图形?相应的边心距把其中每一个图形又分成了两个怎样的图形?
(9)如果正三角形的边长为a,那么它的外接圆的半径r和内切圆的半径d分别是多少?它们之间满足什么关系?一般地,如果正n边形的边长为an,半为rn,边心距为dn,这三个量之间有什么关系?
(10)以正n边形的中心O为旋转中心,将正n边形旋转 ,你能得到什么结论?
(11)正n边形是中心对称图形吗?
三、典型例题
一个正六边形花坛的半径为R,求花坛的边长a,周长p和面积S
四、课堂小结 本节课你有什么收获?
五、当堂检测
1. 下面的命题是真命题吗?如果不是,请举出一个反例.
(1)正多边形的对称轴是经过正多边形的顶点和中心的直线;
(2)边数为偶数的正多边形,既是轴对称图形又是中心对称图形;
(3)既是轴对称图形,又是中心对称图形的多边形是正多边形;
(4)有一个外接圆和一个内切圆的多边形是正多边形.
2.完成下表中正多边形的计算,并把计算结果填入表内:
边数n 内角α 中心角αn 半径Rn 边长an 边心距rn 周长Pn 面积Sn
3
4
6
六、自主评价
学习目标 表现程度 例1 例2 例3
A B C
了解正多边形的概念 了解 不确定 不了解
了解正多边形与圆的关系 了解 不确定 不了解
能运用正多边形的边长、半径、边心距等进行计算 能 不确定 不能
七、课后分层作业
【基础闯关】
1.下列命题正确的是( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等,各角也相等的多边形是正多边形
2.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为( )
A.30° B.36° C.45° D.60°
3.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
4.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和的长分别为( )
A.2, B.2,π C., D.2,
5.如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
A. B.20 C.18 D.
6.如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2﹣r2=a2 B.a=2Rsin36°
C.a=2rtan36° D.r=Rcos36°
第2题 第4题 第5题 第6题
【能力提升】
7.如图,四边形ABCD是⊙O的内接正四边形,分别以点A,O为圆心,取大于OA的定长为半径画弧,两弧相交于点M,N,作直线MN,交⊙O于点E,F.若OA=1,则,AE,AB所围成的阴影部分面积为 .
8.如图,A,B,C是⊙O上顺次三点,若AC,AB,BC分别是⊙O内接正三角形,正方形,正n边形的一边,则n= .
9.如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2,求图中阴影部分的面积.
【培优创新】
10.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)图1中∠MON的度数是 ;
(2)在图2中∠MON的度数是 ,图3中∠MON的度数是 ;
(3)若M、N分别是正n边形ABCDE…的边AB、BC上的点,且BM=CN.连接OM、ON,你认为∠MON的度数是 (直接写出答案)
【学习目标】
1.了解正多边形的概念及正多边形与圆的关系
2.能运用正多边形的边长、半径、边心距等进行计算
【学习重点】正多边形的概念及正多边形与圆的关系
【学习难点】正多边形性质的应用
【学习过程】
一、复习引入
你还记得什么叫正多边形吗?说出你常见的几种正多边形。
二、新知探究
探究一:观察下面的正多边形,思考下面的问题:
(1)它们都是轴对称图形吗?如果是,分别画出每个图形所有的对称轴,并说出这些对称轴是怎样的直线.
(2)正三角形有几条对称轴?正四边形、正五边形、正六边形呢?由此你能猜测正n边形有几条对称轴吗?
知识点1.正多边形的对称性
正多边形都是______________,一个正n边形有_____条对称轴
(3)通过画图,你发现正多边形的各条对称轴有怎样的特征?由此你能推出正多边形的什么性质?
知识点2.正多边形对称轴特征
正多边形的各条对称轴_________,这点到正多边形的各个顶点的距离相等,到__________也相等.
(4)利用尺规作出一个正三角形的外接圆和内切圆,你发现正三角形的外接圆的圆心与内切圆的圆心有什么特征?
(5)画出一个正方形,你能说出它的外接圆和内切圆的位置吗?你发现正方形的外接圆与内切圆有什么特征?
(6)由(4)(5)你猜测正多边形都有外接圆和内切圆吗?如果有,它们的外接圆与内切圆有什么特征?
知识点2.
任何正多边形都有一个______和一个_______,这两个圆是同心圆,圆心是各对称轴的交点。
【跟踪练习】
探究二:如图,正多边形的外接圆和内切圆的公共圆心叫做正多边形的______,外接圆的半径叫做_____________,内切圆的半径叫做正多边形的________。可以看出,正多边形各边所对的外接圆的圆心角都相等. 正多边形每一边所对的外接圆的圆心角叫做正多边形的______,正n边形的每个中心角都等于__________.
(7)你能分别说出图中正方形与正六边形的中心、半径、边心距和中心角的度数吗?
(8)正n边形的n条半径把正n边形分成了n个怎样的图形?相应的边心距把其中每一个图形又分成了两个怎样的图形?
(9)如果正三角形的边长为a,那么它的外接圆的半径r和内切圆的半径d分别是多少?它们之间满足什么关系?一般地,如果正n边形的边长为an,半为rn,边心距为dn,这三个量之间有什么关系?
(10)以正n边形的中心O为旋转中心,将正n边形旋转 ,你能得到什么结论?
(11)正n边形是中心对称图形吗?
三、典型例题
一个正六边形花坛的半径为R,求花坛的边长a,周长p和面积S
四、课堂小结 本节课你有什么收获?
五、当堂检测
1. 下面的命题是真命题吗?如果不是,请举出一个反例.
(1)正多边形的对称轴是经过正多边形的顶点和中心的直线;
(2)边数为偶数的正多边形,既是轴对称图形又是中心对称图形;
(3)既是轴对称图形,又是中心对称图形的多边形是正多边形;
(4)有一个外接圆和一个内切圆的多边形是正多边形.
2.完成下表中正多边形的计算,并把计算结果填入表内:
边数n 内角α 中心角αn 半径Rn 边长an 边心距rn 周长Pn 面积Sn
3
4
6
六、自主评价
学习目标 表现程度 例1 例2 例3
A B C
了解正多边形的概念 了解 不确定 不了解
了解正多边形与圆的关系 了解 不确定 不了解
能运用正多边形的边长、半径、边心距等进行计算 能 不确定 不能
七、课后分层作业
【基础闯关】
1.下列命题正确的是( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等,各角也相等的多边形是正多边形
2.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为( )
A.30° B.36° C.45° D.60°
3.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
4.如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和的长分别为( )
A.2, B.2,π C., D.2,
5.如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
A. B.20 C.18 D.
6.如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
A.R2﹣r2=a2 B.a=2Rsin36°
C.a=2rtan36° D.r=Rcos36°
第2题 第4题 第5题 第6题
【能力提升】
7.如图,四边形ABCD是⊙O的内接正四边形,分别以点A,O为圆心,取大于OA的定长为半径画弧,两弧相交于点M,N,作直线MN,交⊙O于点E,F.若OA=1,则,AE,AB所围成的阴影部分面积为 .
8.如图,A,B,C是⊙O上顺次三点,若AC,AB,BC分别是⊙O内接正三角形,正方形,正n边形的一边,则n= .
9.如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2,求图中阴影部分的面积.
【培优创新】
10.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE的边AB、BC上的点,且BM=CN,连接OM、ON.
(1)图1中∠MON的度数是 ;
(2)在图2中∠MON的度数是 ,图3中∠MON的度数是 ;
(3)若M、N分别是正n边形ABCDE…的边AB、BC上的点,且BM=CN.连接OM、ON,你认为∠MON的度数是 (直接写出答案)
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
