3.6 弧长及扇形面积的计算 学案(无答案)2024-2025学年青岛版九年级上册
文档属性
| 名称 | 3.6 弧长及扇形面积的计算 学案(无答案)2024-2025学年青岛版九年级上册 | 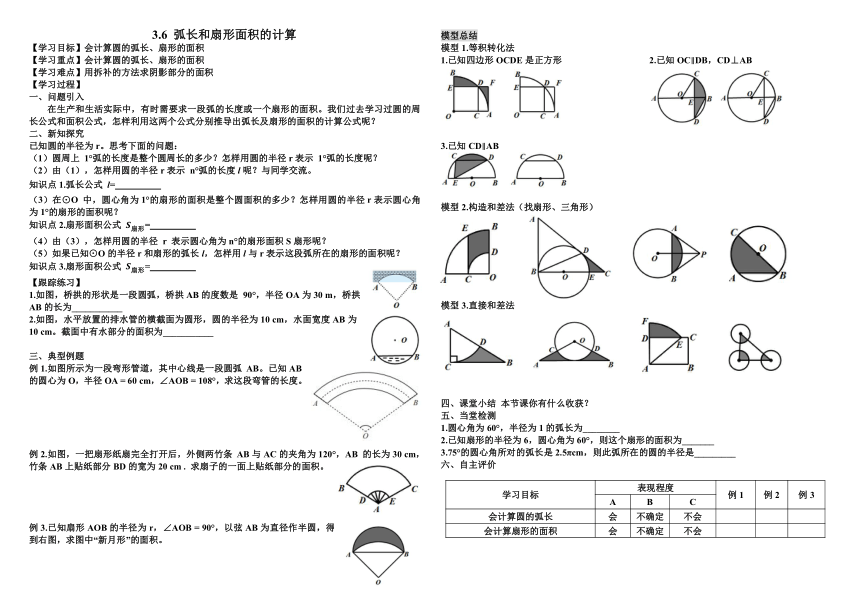 | |
| 格式 | docx | ||
| 文件大小 | 220.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 15:38:41 | ||
图片预览

文档简介
3.6 弧长和扇形面积的计算
【学习目标】会计算圆的弧长、扇形的面积
【学习重点】会计算圆的弧长、扇形的面积
【学习难点】用拆补的方法求阴影部分的面积
【学习过程】
一、问题引入
在生产和生活实际中,有时需要求一段弧的长度或一个扇形的面积。我们过去学习过圆的周长公式和面积公式,怎样利用这两个公式分别推导出弧长及扇形的面积的计算公式呢?
二、新知探究
已知圆的半径为r。思考下面的问题:
(1)圆周上 1°弧的长度是整个圆周长的多少?怎样用圆的半径r表示 1°弧的长度呢?
(2)由(1),怎样用圆的半径r表示 n°弧的长度l呢?与同学交流。
知识点1.弧长公式 l=
(3)在⊙O 中,圆心角为1°的扇形的面积是整个圆面积的多少?怎样用圆的半径r表示圆心角为1°的扇形的面积呢?
知识点2.扇形面积公式 =
(4)由(3),怎样用圆的半径 r 表示圆心角为n°的扇形面积S扇形呢?
(5)如果已知⊙O的半径r和扇形的弧长l,怎样用l与r表示这段弧所在的扇形的面积呢?
知识点3.扇形面积公式 =
【跟踪练习】
1.如图,桥拱的形状是一段圆弧,桥拱AB的度数是 90°,半径OA为30 m,桥拱AB的长为___________
2.如图,水平放置的排水管的横截面为圆形,圆的半径为10 cm,水面宽度AB为10 cm。截面中有水部分的面积为___________
三、典型例题
例1.如图所示为一段弯形管道,其中心线是一段圆弧 AB。已知AB的圆心为O,半径OA = 60 cm,∠AOB = 108°,求这段弯管的长度。
例2.如图,一把扇形纸扇完全打开后,外侧两竹条 AB与AC的夹角为120°,AB 的长为30 cm,竹条AB上贴纸部分BD的宽为20 cm . 求扇子的一面上贴纸部分的面积。
例3.已知扇形AOB的半径为r,∠AOB = 90°,以弦AB为直径作半圆,得到右图,求图中“新月形”的面积。
模型总结
模型1.等积转化法
1.已知四边形OCDE是正方形 2.已知OCDB,CD⊥AB
3.已知CDAB
模型2.构造和差法(找扇形、三角形)
模型3.直接和差法
四、课堂小结 本节课你有什么收获?
五、当堂检测
1.圆心角为60°,半径为1的弧长为________
2.已知扇形的半径为6,圆心角为60°,则这个扇形的面积为_______
3.75°的圆心角所对的弧长是2.5πcm,则此弧所在的圆的半径是_________
六、自主评价
学习目标 表现程度 例1 例2 例3
A B C
会计算圆的弧长 会 不确定 不会
会计算扇形的面积 会 不确定 不会
七、课后分层作业
【基础闯关】
1.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,半径OA=90m,圆心角∠AOB=80°,则这段弯路()的长度为( )
A.20πm B.30πm C.40πm D.50πm
2.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2m,则改建后门洞的圆弧长是( )
A.m B.m C.m D.(+2)m
3.如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=4m,OB=2m,则阴影部分的面积是( )
A.π B.π C.4π D.π
4.如图.将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接AC.若OA=2,则图中阴影部分的面积是( )
A. B. C. D.
第1题 第2题 第3题 第4题
5.如图,在矩形ABCD中,AB=1,BC=2,以B为圆心,BC的长为半径画弧,交AD于点E.则图中阴影部分的面积为 .(结果保留π)
6.如图,⊙A,⊙B,⊙C两两不相交,且半径都等于2,则图中三个扇形(即阴影部分)的面积之和为 .(结果保留π)
【能力提升】
7.如图,等边三角形ABC中,将边AC逐渐变成以BA为半径的,其他两边的长度不变,则∠ABC的度数大小由60变为( )
A. B. C. D.
8.如图:AD是⊙O的直径,AD=12,点BC在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°,则以下判断中不正确的是( )
A.∠ADE=∠E B.劣弧AB的长为π C.点C为弧BD的中点 D.BD平分∠ADE
9.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为,则图中阴影部分的面积是
10.如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置时,若AB=2,AD=4,则阴影部分的面积为
11.如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为
第8题 第9题 第10题 第11题
12.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2厘米的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为 平方厘米.(圆周率用π表示)
13.如图,AB是⊙O的直径,C为⊙O上一点,且AB⊥OC,P为圆上一动点,M为AP的中点,连接CM.若⊙O的半径为2,则CM长的最大值是 .
【培优创新】
14.如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2;以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3;以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;….按此做法进行下去,其中弧P2022O2023的长为 .
第12题 第13题 第14题
【学习目标】会计算圆的弧长、扇形的面积
【学习重点】会计算圆的弧长、扇形的面积
【学习难点】用拆补的方法求阴影部分的面积
【学习过程】
一、问题引入
在生产和生活实际中,有时需要求一段弧的长度或一个扇形的面积。我们过去学习过圆的周长公式和面积公式,怎样利用这两个公式分别推导出弧长及扇形的面积的计算公式呢?
二、新知探究
已知圆的半径为r。思考下面的问题:
(1)圆周上 1°弧的长度是整个圆周长的多少?怎样用圆的半径r表示 1°弧的长度呢?
(2)由(1),怎样用圆的半径r表示 n°弧的长度l呢?与同学交流。
知识点1.弧长公式 l=
(3)在⊙O 中,圆心角为1°的扇形的面积是整个圆面积的多少?怎样用圆的半径r表示圆心角为1°的扇形的面积呢?
知识点2.扇形面积公式 =
(4)由(3),怎样用圆的半径 r 表示圆心角为n°的扇形面积S扇形呢?
(5)如果已知⊙O的半径r和扇形的弧长l,怎样用l与r表示这段弧所在的扇形的面积呢?
知识点3.扇形面积公式 =
【跟踪练习】
1.如图,桥拱的形状是一段圆弧,桥拱AB的度数是 90°,半径OA为30 m,桥拱AB的长为___________
2.如图,水平放置的排水管的横截面为圆形,圆的半径为10 cm,水面宽度AB为10 cm。截面中有水部分的面积为___________
三、典型例题
例1.如图所示为一段弯形管道,其中心线是一段圆弧 AB。已知AB的圆心为O,半径OA = 60 cm,∠AOB = 108°,求这段弯管的长度。
例2.如图,一把扇形纸扇完全打开后,外侧两竹条 AB与AC的夹角为120°,AB 的长为30 cm,竹条AB上贴纸部分BD的宽为20 cm . 求扇子的一面上贴纸部分的面积。
例3.已知扇形AOB的半径为r,∠AOB = 90°,以弦AB为直径作半圆,得到右图,求图中“新月形”的面积。
模型总结
模型1.等积转化法
1.已知四边形OCDE是正方形 2.已知OCDB,CD⊥AB
3.已知CDAB
模型2.构造和差法(找扇形、三角形)
模型3.直接和差法
四、课堂小结 本节课你有什么收获?
五、当堂检测
1.圆心角为60°,半径为1的弧长为________
2.已知扇形的半径为6,圆心角为60°,则这个扇形的面积为_______
3.75°的圆心角所对的弧长是2.5πcm,则此弧所在的圆的半径是_________
六、自主评价
学习目标 表现程度 例1 例2 例3
A B C
会计算圆的弧长 会 不确定 不会
会计算扇形的面积 会 不确定 不会
七、课后分层作业
【基础闯关】
1.如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,半径OA=90m,圆心角∠AOB=80°,则这段弯路()的长度为( )
A.20πm B.30πm C.40πm D.50πm
2.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m,高为2m,则改建后门洞的圆弧长是( )
A.m B.m C.m D.(+2)m
3.如图是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=4m,OB=2m,则阴影部分的面积是( )
A.π B.π C.4π D.π
4.如图.将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接AC.若OA=2,则图中阴影部分的面积是( )
A. B. C. D.
第1题 第2题 第3题 第4题
5.如图,在矩形ABCD中,AB=1,BC=2,以B为圆心,BC的长为半径画弧,交AD于点E.则图中阴影部分的面积为 .(结果保留π)
6.如图,⊙A,⊙B,⊙C两两不相交,且半径都等于2,则图中三个扇形(即阴影部分)的面积之和为 .(结果保留π)
【能力提升】
7.如图,等边三角形ABC中,将边AC逐渐变成以BA为半径的,其他两边的长度不变,则∠ABC的度数大小由60变为( )
A. B. C. D.
8.如图:AD是⊙O的直径,AD=12,点BC在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°,则以下判断中不正确的是( )
A.∠ADE=∠E B.劣弧AB的长为π C.点C为弧BD的中点 D.BD平分∠ADE
9.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为,则图中阴影部分的面积是
10.如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置时,若AB=2,AD=4,则阴影部分的面积为
11.如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A、B、C、D不重合),经过P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为
第8题 第9题 第10题 第11题
12.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2厘米的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为 平方厘米.(圆周率用π表示)
13.如图,AB是⊙O的直径,C为⊙O上一点,且AB⊥OC,P为圆上一动点,M为AP的中点,连接CM.若⊙O的半径为2,则CM长的最大值是 .
【培优创新】
14.如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2;以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3;以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;….按此做法进行下去,其中弧P2022O2023的长为 .
第12题 第13题 第14题
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
