人教B版高中数学必修第一册第三章函数3.3函数的应用(一) 课件(共15张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册第三章函数3.3函数的应用(一) 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
因为函数可以描述一个量依赖于另外一个量变化而变化的情况,所以函数知识在实际生活中有着广泛的应用.下面我们就一起探究一下怎么利用学过的知识来解决.
到目前为止,我们已经学习了哪些常用函数?
1.了解一次函数、二次函数、分段函数的广泛应用并求解实际问题. (重点)
2.掌握求解函数应用题的基本步骤. (难点)
3.掌握对数据的合理处理,建立函数模型. (难点)
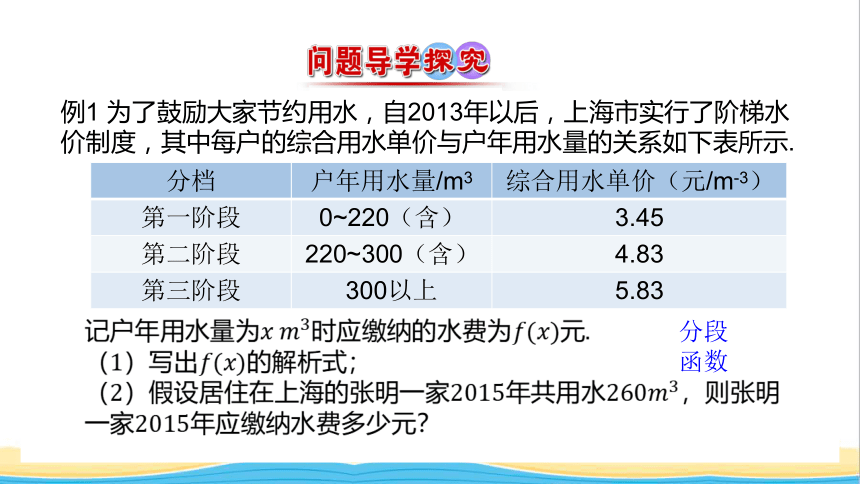
例1 为了鼓励大家节约用水,自2013年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示.
分档 户年用水量/m3 综合用水单价(元/m-3)
第一阶段 0~220(含) 3.45
第二阶段 220~300(含) 4.83
第三阶段 300以上 5.83
分段函数
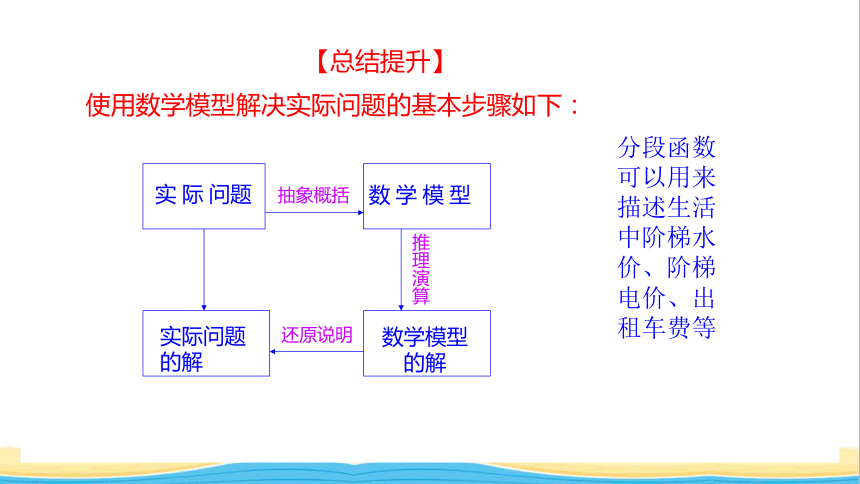
【总结提升】
使用数学模型解决实际问题的基本步骤如下:
实 际 问题
数 学 模 型
实际问题 的解
数学模型
的解
抽象概括
推理演算
还原说明
分段函数可以用来描述生活中阶梯水价、阶梯电价、出租车费等
例3 某农家旅游公司有客房160间,每间房单价为200元时,每天都客满.已知每间房单价每提高20元,则客房出租数就会减少10间.若不考虑其他因素,旅游公司把每间房单价提高到多少时,每天客房的租金总收入最高?
【分析】房价与租金总收入的关系可以通过列表分析:
能看出数据变化的规律吗?
提价/元 每间房单价/元 客房出租数 租金总收入/元
0 200 160 32000
20 220 150 33000
40 240 140 33600
60 260 130 33800
此函数的定义域是什么?
二次函数求最值
均值不等式求最值
某桶装水经营部每天的房租、人员工资等固
定成本为200元,每桶水的进价是5元.销售单价
与日均销售量的关系如下表所示:
请根据以上数据作出分析,这个经营部怎样定价
才能获得最大利润?
【变式练习】
销售单价(元) 6 7 8 9 10 11 12
日均销售量(桶) 480 440 400 360 320 280 240
数 学 模 型
实际问题的解
数学模型的解
抽象概括
推理演算
还原说明
因为函数可以描述一个量依赖于另外一个量变化而变化的情况,所以函数知识在实际生活中有着广泛的应用.下面我们就一起探究一下怎么利用学过的知识来解决.
到目前为止,我们已经学习了哪些常用函数?
1.了解一次函数、二次函数、分段函数的广泛应用并求解实际问题. (重点)
2.掌握求解函数应用题的基本步骤. (难点)
3.掌握对数据的合理处理,建立函数模型. (难点)
例1 为了鼓励大家节约用水,自2013年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示.
分档 户年用水量/m3 综合用水单价(元/m-3)
第一阶段 0~220(含) 3.45
第二阶段 220~300(含) 4.83
第三阶段 300以上 5.83
分段函数
【总结提升】
使用数学模型解决实际问题的基本步骤如下:
实 际 问题
数 学 模 型
实际问题 的解
数学模型
的解
抽象概括
推理演算
还原说明
分段函数可以用来描述生活中阶梯水价、阶梯电价、出租车费等
例3 某农家旅游公司有客房160间,每间房单价为200元时,每天都客满.已知每间房单价每提高20元,则客房出租数就会减少10间.若不考虑其他因素,旅游公司把每间房单价提高到多少时,每天客房的租金总收入最高?
【分析】房价与租金总收入的关系可以通过列表分析:
能看出数据变化的规律吗?
提价/元 每间房单价/元 客房出租数 租金总收入/元
0 200 160 32000
20 220 150 33000
40 240 140 33600
60 260 130 33800
此函数的定义域是什么?
二次函数求最值
均值不等式求最值
某桶装水经营部每天的房租、人员工资等固
定成本为200元,每桶水的进价是5元.销售单价
与日均销售量的关系如下表所示:
请根据以上数据作出分析,这个经营部怎样定价
才能获得最大利润?
【变式练习】
销售单价(元) 6 7 8 9 10 11 12
日均销售量(桶) 480 440 400 360 320 280 240
数 学 模 型
实际问题的解
数学模型的解
抽象概括
推理演算
还原说明
