人教B版高中数学必修第一册第三章函数3.4数学建模:活动决定苹果的最佳出售时间点 课件(共32张PPT)
文档属性
| 名称 | 人教B版高中数学必修第一册第三章函数3.4数学建模:活动决定苹果的最佳出售时间点 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 16:05:42 | ||
图片预览











文档简介
(共32张PPT)
人教B版 数学 必修第一册
课标定位素养阐释
1.了解数学建模的意义.
2.了解数学建模的基本过程.
3.能够运用已有函数模型或建立函数模型解决实际问题.
4.经历数学建模的全过程,提升数学建模、数学抽象、数据分析、数学运算、逻辑推理和直观想象素养.
一、数学建模简介
1.数学建模的概念
对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题就是数学建模.
2.数学建模的过程
发现问题提出问题——根据现实生活和生产的实际情况,切合问题的实际背景,发现需要解决的问题,提出具有实际意义的问题
↓
分析问题建立模型——在分析实际问题的基础上,利用适当的数学工具来刻画各变量、常量之间的数学关系,建立相应的数学模型(尽量用简单的数学模型)
↓
确定参数计算求解——利用调查研究获取的数据资料,把数据代入数学模型进行计算,求出参数的值(或近似值)
↓
验证结果改进模型——将模型分析结果与实际情形进行比较,以此来验证模型的准确性、合理性和适用性.如果模型与实际较吻合,则要对计算结果给出其实际含义,并进行解释.如果模型与实际吻合较差,则应该修改假设,再次重复建模过程对模型进行改进
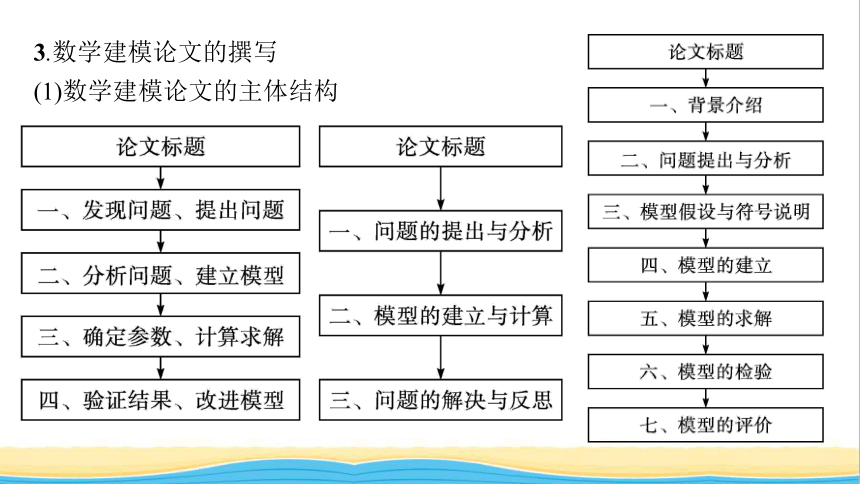
3.数学建模论文的撰写
(1)数学建模论文的主体结构
(2)撰写数学建模论文的要求
①数学建模的过程中,往往采用分工合作的方式进行.
②一个数学建模小组由3—5人组成.理想的小组中,既要有数学基础扎实的同学,也要有能熟练使用计算机的同学,还要有写作表达能力强的同学.
二、建立函数模型解决实际问题实例
1.利用已有函数模型解决实际问题
【典例1】 汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停止,我们称这段距离为“刹车距离”.刹车距离是分析事故原因的一个重要因素.在一个限速为40 km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查,测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的刹车距离s(单位:m)与车速x(单位:km/h)之间分别有如下关系:s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.试判断甲、乙两车有无超速现象,并根据所学数学知识给出判断的依据.
分析:根据已经给出的刹车距离与车速的函数关系,由刹车距离建立不等式,求出两辆车的车速范围,然后进行判断.
解:依题意可得,甲车的刹车距离s甲=0.1x+0.01x2>12,即x2+10x-1 200>0,
解得x>30或x<-40(不符合实际意义,舍去),这说明,甲车的速度超过30 km/h.
但根据题意,刹车距离略超过12 m,由此估计甲车速度不会超过限速
40 km/h.
乙车的刹车距离s乙=0.05x+0.005x2>10,即x2+10x-2 000>0,
解得x>40或x<-50(不合实际意义,舍去),
这表明乙车的车速超过40 km/h,超过规定限速.
综上所述,甲车没有超速现象,乙车有超速现象.
求解所给函数模型解决实际问题的关注点
(1)认清所给函数模型,弄清哪些量为待定系数.
(2)根据已知利用待定系数法,确定模型中的待定系数.
(3)利用该模型求解实际问题.
【变式训练1】 某地上年度电价为0.8元/千瓦时,年用电量为1亿千瓦时.本年度计划将电价调至0.55~0.75元/千瓦时,经测算,若电价调至x元/千瓦时,则本年度新增用电量y(单位:亿千瓦时)与(x-0.4)成反比例.又当x=0.65时,y=0.8.
(1)求y与x之间的函数解析式;
(2)若每千瓦时电的成本价为0.3元/千瓦时,则当电价调至多少时,本年度电力部门的收益将比上年度增加20% [收益=用电量×(实际电价一成本价)]
整理,得x2-1.1x+0.3=0,
解得x1=0.5,x2=0.6.
经检验x1=0.5,x2=0.6都是原方程的根.
∵0.55≤x≤0.75,
∴x=0.6.
故当电价调至0.6元/千瓦时,本年度电力部门的收益将比上年度增加20%.
2.建立函数模型解决实际问题
【典例2】 据气象中心观察和预测:发生于沿海M地的台风一直向正南方向移动,其移动速度v(单位:km/h)与时间t(单位:h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即t h内台风所经过的路程s km.
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地的正南方向,且距M地650 km,试判断这场台风是否会侵袭到N城.如果会,那么在台风发生后多长时间它将侵袭到N城 如果不会,请说明理由.
分析:(1)由图象求出直线OA的方程,把t=4代入可得s的值;
(2)由图象分析可知s是关于t的分段函数,分三段求出即可;
(3)利用(2)中所得的函数的值域求解.
(3)当t∈[0,10]时,smax= ×102=150<650;
当t∈(10,20]时,smax=30×20-150=450<650;
当t∈(20,35]时,令-t2+70t-550=650,
解得t=30或t=40(舍去),
故在台风发生30 h后将侵袭到N城.
1.解函数应用题的一般程序
第一步:审题.
第二步:建模.
第三步:解模.
第四步:还原.
第五步:反思.
2.把实际问题数学模型化要过好三关
(1)事理关:通过阅读、理解,明确问题讲的是什么,熟悉实际背景,为解题找出突破口.
(2)文理关:将实际问题的文字语言转化为数学符号语言,用数学式子表达数学关系.
(3)数理关:在构建数学模型的过程中,对已知数学知识进行检索,从而认定或构建相应的数学模型.
【变式训练2】 已知某公司生产某款手机的年固定成本为40万元,每生产1万部还需另投入16万元.设该公司一年内共生产该款手机x万部并全部销
售完,每万部的销售收入为R(x)万元,且
(1)写出年利润W(单位:万元)关于年产量x(单位:万部)的函数解析式;
(2)当年产量为多少万部时,该公司在该款手机的生产中所获得的利润最大 并求出最大利润.
当且仅当 =16x,即x=50∈(40,+∞)时,等号成立,所以W的最大值为
5 760.
综合①②知,当x=32时,W取得最大值6 104万元,即当年产量为32万部时,该公司在该款手机的生产中所获得的利润最大,且最大利润为6 104万元.
【典例3】
发现问题、提出问题
天然气是清洁能源,很多家庭的一日三餐都要用天然气来做.为了研究燃气灶在何种情况下最省气,某学校数学建模小组通过实验得到了如下数据:
燃气灶旋钮在不同位置时烧开一壶水的天然气用量
位置 开始时燃气表读数/m3 水开时燃气表读数/m3 天然气用量/m3
18° 9.080 9.210 0.130
36° 8.958 9.080 0.122
54° 8.819 8.958 0.139
72° 8.670 8.819 0.149
90° 8.498 8.670 0.172
分析问题、建立模型
用表内数据,在直角坐标系上标出各点.
由图可以看出,5个点显示出随着旋钮的角度逐渐增大,天然气用量有一个从大到小又从小到大的过程.在我们学习过的函数图象中,二次函数的图象与之最接近,可以用二次函数近似地表示这种变化.
确定参数、计算求解:
设函数解析式为y=ax2+bx+c,取三对数据即可求出解析式的系数,不妨取
(18,0.130),(36,0.122),(90,0.172),得方程组
解得a≈1.903 3×10-5,b≈-1.472 2×10-3,c≈1.503 3×10-1.
故函数解析式为y=1.903 3×10-5x2-1.472 2×10-3x+1.503 3×10-1.
求天然气用量最少时的旋钮位置,实际上是求函数
y=1.903 3×10-5x2-1.472 2×10-3x+1.503 3×10-1的最小值点x0.
即天然气用量最少时的旋钮位置是旋转39°的位置,这时的天然气用量大约是
验证结果、改进模型
对于上一个步骤中得到的天然气用量的函数模型
y=1.903 3×10-5x2-1.472 2×10-3x+1.503 3×10-1能够很好地反映天然气用量y与旋钮位置x的关系吗 试选择一个数据进行验证.
当x=54时,由函数的解析式可得y≈0.126 3(m3),和实验所得数据的差为0.139-0.126 3=0.012 7,数值很小,该函数模型可以很好地反映用气量y与旋钮位置x的关系.
建立函数模型解决
问题的框图表示
【变式训练3】 房屋造价(单位:元/m2)与建筑层数有关,可表示为一般造价(单位:元/m2)乘层数系数λ.根据经验数据,绘出层数系数λ与层数n的关系,如图所示,其中2层到5层的建筑由于共用地基和层顶等原因,λ随层数增加沿抛物线下降,而5层~8层及以上的建筑则由于防震、防风等因素需增加成本,λ随层数增加而增加.
(1)请根据所给图与表格建立λ随层数n增加而改变的函数解析式,并将表中数据填完整;
n 1 2 3 4 5 6 7 8
λ 1.08 1.03 1 1.08 1.17 1.26
(2)某单位为建造楼房筹集资金1 000万元,用于支付房屋造价和土地使用权购置费,若一般造价为800元/m2,土地价为300元/m2,试利用(1)中的条件求该单位最多能建房多少平方米.(精确到1 m2)
解:(1)由题设知,当2≤n≤5时,λ=f(n)的图象为抛物线的一段,所以设λ=an2+bn+c(a≠0),
将(2,1.08)(3,1.03)(4,1)代入,
所以λ=0.01n2-0.1n+1.24.
当5所以设λ=kn+b(k≠0),将(6,1.08)和(8,1.26)代入,
所以λ=0.09n+0.54,
通过验证知(7,1.17)正好在此直线上.
把n=5代入上式,得λ=0.99.
又由图可得n=1时,λ=1.25.
将1.25,0.99填入表中的对应格里即可.
(2)设所建楼房占地面积为x m2,
由(1)知当n=5时,造价最低,此时λ=0.99,
故总建房面积为5x m2,
其总造价为0.99×800×5x+x×300,
依题意得10 000 000≥0.99×800×5x+300x,
人教B版 数学 必修第一册
课标定位素养阐释
1.了解数学建模的意义.
2.了解数学建模的基本过程.
3.能够运用已有函数模型或建立函数模型解决实际问题.
4.经历数学建模的全过程,提升数学建模、数学抽象、数据分析、数学运算、逻辑推理和直观想象素养.
一、数学建模简介
1.数学建模的概念
对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题就是数学建模.
2.数学建模的过程
发现问题提出问题——根据现实生活和生产的实际情况,切合问题的实际背景,发现需要解决的问题,提出具有实际意义的问题
↓
分析问题建立模型——在分析实际问题的基础上,利用适当的数学工具来刻画各变量、常量之间的数学关系,建立相应的数学模型(尽量用简单的数学模型)
↓
确定参数计算求解——利用调查研究获取的数据资料,把数据代入数学模型进行计算,求出参数的值(或近似值)
↓
验证结果改进模型——将模型分析结果与实际情形进行比较,以此来验证模型的准确性、合理性和适用性.如果模型与实际较吻合,则要对计算结果给出其实际含义,并进行解释.如果模型与实际吻合较差,则应该修改假设,再次重复建模过程对模型进行改进
3.数学建模论文的撰写
(1)数学建模论文的主体结构
(2)撰写数学建模论文的要求
①数学建模的过程中,往往采用分工合作的方式进行.
②一个数学建模小组由3—5人组成.理想的小组中,既要有数学基础扎实的同学,也要有能熟练使用计算机的同学,还要有写作表达能力强的同学.
二、建立函数模型解决实际问题实例
1.利用已有函数模型解决实际问题
【典例1】 汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停止,我们称这段距离为“刹车距离”.刹车距离是分析事故原因的一个重要因素.在一个限速为40 km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查,测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的刹车距离s(单位:m)与车速x(单位:km/h)之间分别有如下关系:s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.试判断甲、乙两车有无超速现象,并根据所学数学知识给出判断的依据.
分析:根据已经给出的刹车距离与车速的函数关系,由刹车距离建立不等式,求出两辆车的车速范围,然后进行判断.
解:依题意可得,甲车的刹车距离s甲=0.1x+0.01x2>12,即x2+10x-1 200>0,
解得x>30或x<-40(不符合实际意义,舍去),这说明,甲车的速度超过30 km/h.
但根据题意,刹车距离略超过12 m,由此估计甲车速度不会超过限速
40 km/h.
乙车的刹车距离s乙=0.05x+0.005x2>10,即x2+10x-2 000>0,
解得x>40或x<-50(不合实际意义,舍去),
这表明乙车的车速超过40 km/h,超过规定限速.
综上所述,甲车没有超速现象,乙车有超速现象.
求解所给函数模型解决实际问题的关注点
(1)认清所给函数模型,弄清哪些量为待定系数.
(2)根据已知利用待定系数法,确定模型中的待定系数.
(3)利用该模型求解实际问题.
【变式训练1】 某地上年度电价为0.8元/千瓦时,年用电量为1亿千瓦时.本年度计划将电价调至0.55~0.75元/千瓦时,经测算,若电价调至x元/千瓦时,则本年度新增用电量y(单位:亿千瓦时)与(x-0.4)成反比例.又当x=0.65时,y=0.8.
(1)求y与x之间的函数解析式;
(2)若每千瓦时电的成本价为0.3元/千瓦时,则当电价调至多少时,本年度电力部门的收益将比上年度增加20% [收益=用电量×(实际电价一成本价)]
整理,得x2-1.1x+0.3=0,
解得x1=0.5,x2=0.6.
经检验x1=0.5,x2=0.6都是原方程的根.
∵0.55≤x≤0.75,
∴x=0.6.
故当电价调至0.6元/千瓦时,本年度电力部门的收益将比上年度增加20%.
2.建立函数模型解决实际问题
【典例2】 据气象中心观察和预测:发生于沿海M地的台风一直向正南方向移动,其移动速度v(单位:km/h)与时间t(单位:h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即t h内台风所经过的路程s km.
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地的正南方向,且距M地650 km,试判断这场台风是否会侵袭到N城.如果会,那么在台风发生后多长时间它将侵袭到N城 如果不会,请说明理由.
分析:(1)由图象求出直线OA的方程,把t=4代入可得s的值;
(2)由图象分析可知s是关于t的分段函数,分三段求出即可;
(3)利用(2)中所得的函数的值域求解.
(3)当t∈[0,10]时,smax= ×102=150<650;
当t∈(10,20]时,smax=30×20-150=450<650;
当t∈(20,35]时,令-t2+70t-550=650,
解得t=30或t=40(舍去),
故在台风发生30 h后将侵袭到N城.
1.解函数应用题的一般程序
第一步:审题.
第二步:建模.
第三步:解模.
第四步:还原.
第五步:反思.
2.把实际问题数学模型化要过好三关
(1)事理关:通过阅读、理解,明确问题讲的是什么,熟悉实际背景,为解题找出突破口.
(2)文理关:将实际问题的文字语言转化为数学符号语言,用数学式子表达数学关系.
(3)数理关:在构建数学模型的过程中,对已知数学知识进行检索,从而认定或构建相应的数学模型.
【变式训练2】 已知某公司生产某款手机的年固定成本为40万元,每生产1万部还需另投入16万元.设该公司一年内共生产该款手机x万部并全部销
售完,每万部的销售收入为R(x)万元,且
(1)写出年利润W(单位:万元)关于年产量x(单位:万部)的函数解析式;
(2)当年产量为多少万部时,该公司在该款手机的生产中所获得的利润最大 并求出最大利润.
当且仅当 =16x,即x=50∈(40,+∞)时,等号成立,所以W的最大值为
5 760.
综合①②知,当x=32时,W取得最大值6 104万元,即当年产量为32万部时,该公司在该款手机的生产中所获得的利润最大,且最大利润为6 104万元.
【典例3】
发现问题、提出问题
天然气是清洁能源,很多家庭的一日三餐都要用天然气来做.为了研究燃气灶在何种情况下最省气,某学校数学建模小组通过实验得到了如下数据:
燃气灶旋钮在不同位置时烧开一壶水的天然气用量
位置 开始时燃气表读数/m3 水开时燃气表读数/m3 天然气用量/m3
18° 9.080 9.210 0.130
36° 8.958 9.080 0.122
54° 8.819 8.958 0.139
72° 8.670 8.819 0.149
90° 8.498 8.670 0.172
分析问题、建立模型
用表内数据,在直角坐标系上标出各点.
由图可以看出,5个点显示出随着旋钮的角度逐渐增大,天然气用量有一个从大到小又从小到大的过程.在我们学习过的函数图象中,二次函数的图象与之最接近,可以用二次函数近似地表示这种变化.
确定参数、计算求解:
设函数解析式为y=ax2+bx+c,取三对数据即可求出解析式的系数,不妨取
(18,0.130),(36,0.122),(90,0.172),得方程组
解得a≈1.903 3×10-5,b≈-1.472 2×10-3,c≈1.503 3×10-1.
故函数解析式为y=1.903 3×10-5x2-1.472 2×10-3x+1.503 3×10-1.
求天然气用量最少时的旋钮位置,实际上是求函数
y=1.903 3×10-5x2-1.472 2×10-3x+1.503 3×10-1的最小值点x0.
即天然气用量最少时的旋钮位置是旋转39°的位置,这时的天然气用量大约是
验证结果、改进模型
对于上一个步骤中得到的天然气用量的函数模型
y=1.903 3×10-5x2-1.472 2×10-3x+1.503 3×10-1能够很好地反映天然气用量y与旋钮位置x的关系吗 试选择一个数据进行验证.
当x=54时,由函数的解析式可得y≈0.126 3(m3),和实验所得数据的差为0.139-0.126 3=0.012 7,数值很小,该函数模型可以很好地反映用气量y与旋钮位置x的关系.
建立函数模型解决
问题的框图表示
【变式训练3】 房屋造价(单位:元/m2)与建筑层数有关,可表示为一般造价(单位:元/m2)乘层数系数λ.根据经验数据,绘出层数系数λ与层数n的关系,如图所示,其中2层到5层的建筑由于共用地基和层顶等原因,λ随层数增加沿抛物线下降,而5层~8层及以上的建筑则由于防震、防风等因素需增加成本,λ随层数增加而增加.
(1)请根据所给图与表格建立λ随层数n增加而改变的函数解析式,并将表中数据填完整;
n 1 2 3 4 5 6 7 8
λ 1.08 1.03 1 1.08 1.17 1.26
(2)某单位为建造楼房筹集资金1 000万元,用于支付房屋造价和土地使用权购置费,若一般造价为800元/m2,土地价为300元/m2,试利用(1)中的条件求该单位最多能建房多少平方米.(精确到1 m2)
解:(1)由题设知,当2≤n≤5时,λ=f(n)的图象为抛物线的一段,所以设λ=an2+bn+c(a≠0),
将(2,1.08)(3,1.03)(4,1)代入,
所以λ=0.01n2-0.1n+1.24.
当5
所以λ=0.09n+0.54,
通过验证知(7,1.17)正好在此直线上.
把n=5代入上式,得λ=0.99.
又由图可得n=1时,λ=1.25.
将1.25,0.99填入表中的对应格里即可.
(2)设所建楼房占地面积为x m2,
由(1)知当n=5时,造价最低,此时λ=0.99,
故总建房面积为5x m2,
其总造价为0.99×800×5x+x×300,
依题意得10 000 000≥0.99×800×5x+300x,
