内蒙古自治区呼和浩特市2024-2025学年八年级下学期7月期末考试数学试卷(含详解)
文档属性
| 名称 | 内蒙古自治区呼和浩特市2024-2025学年八年级下学期7月期末考试数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 15:35:34 | ||
图片预览


文档简介
内蒙古自治区呼和浩特市2024-2025学年八年级下学期7月期末数学试题
一、单选题
1.下列式子是二次根式的是( )
A. B. C. D.
2.已知某三角形的三条边长依次为,则该三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰三角形
3.如图,的对角线,相交于点O,点E是的中点,且,则的长是( )
A.5 B. C.10 D.15
4.下面的三个问题中都有两个变量:
①新能源汽车电池充满电后,使用智能驾驶功能匀速耗电,电池剩余电量与使用时间;
②用固定长度的新型导热线型材料,制作矩形形状的芯片散热框架,矩形面积与一边长;
③点燃一根粗细均匀的蜡烛,蜡烛的剩余高度与燃烧时间.
其中,变量与变量之间的函数关系可以用如图所示的图象表示的是( )
A.①② B.②③ C.①③ D.①②③
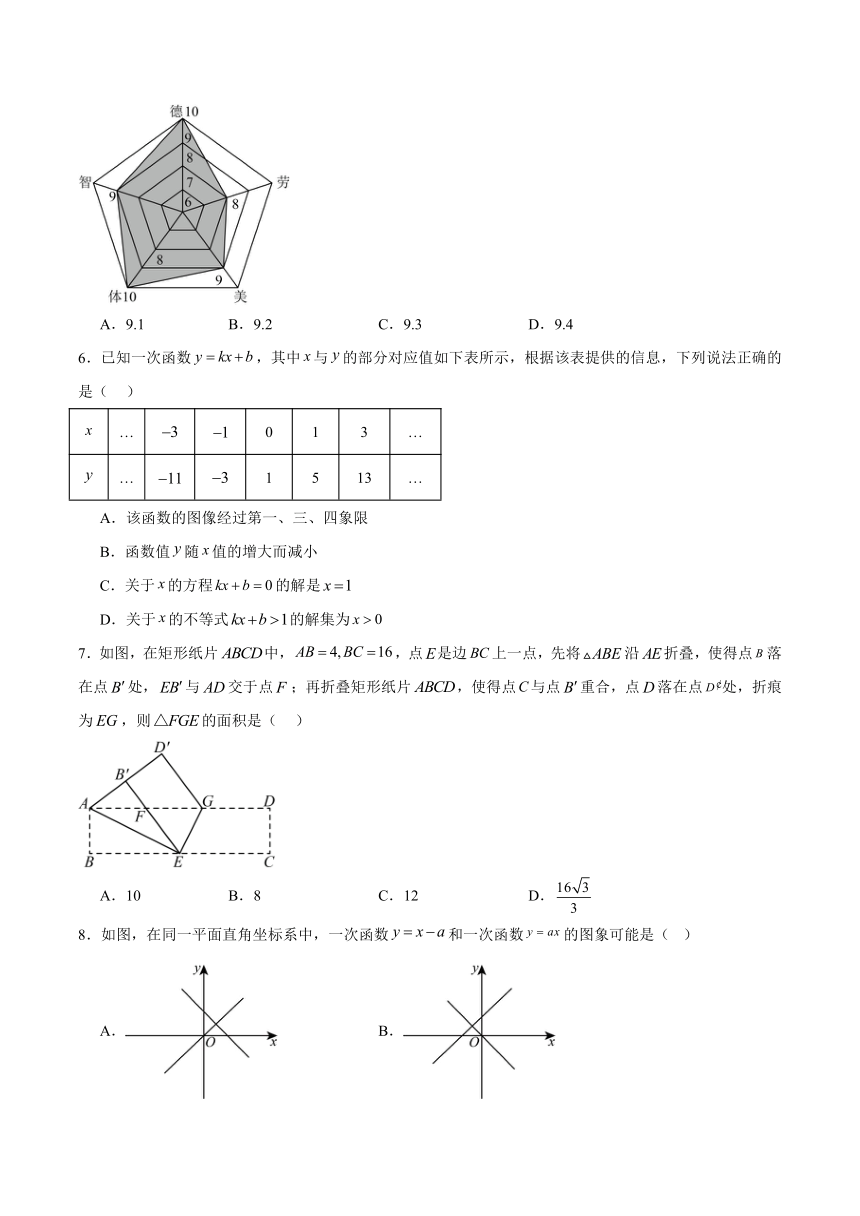
5.某校在学生期末评优工作中,全面贯彻“五育并举”理念,以德智体美劳全面发展为核心标准,依据的权重配比,对学生德、智、体、美、劳五个维度进行量化评分,综合评定学生的最终成绩.小鱼同学本学期这五方面的得分情况如图所示,则小鱼同学期末评优的最终得分是( )
A.9.1 B.9.2 C.9.3 D.9.4
6.已知一次函数,其中与的部分对应值如下表所示,根据该表提供的信息,下列说法正确的是( )
… 0 1 3 …
… 1 5 13 …
A.该函数的图像经过第一、三、四象限
B.函数值随值的增大而减小
C.关于的方程的解是
D.关于的不等式的解集为
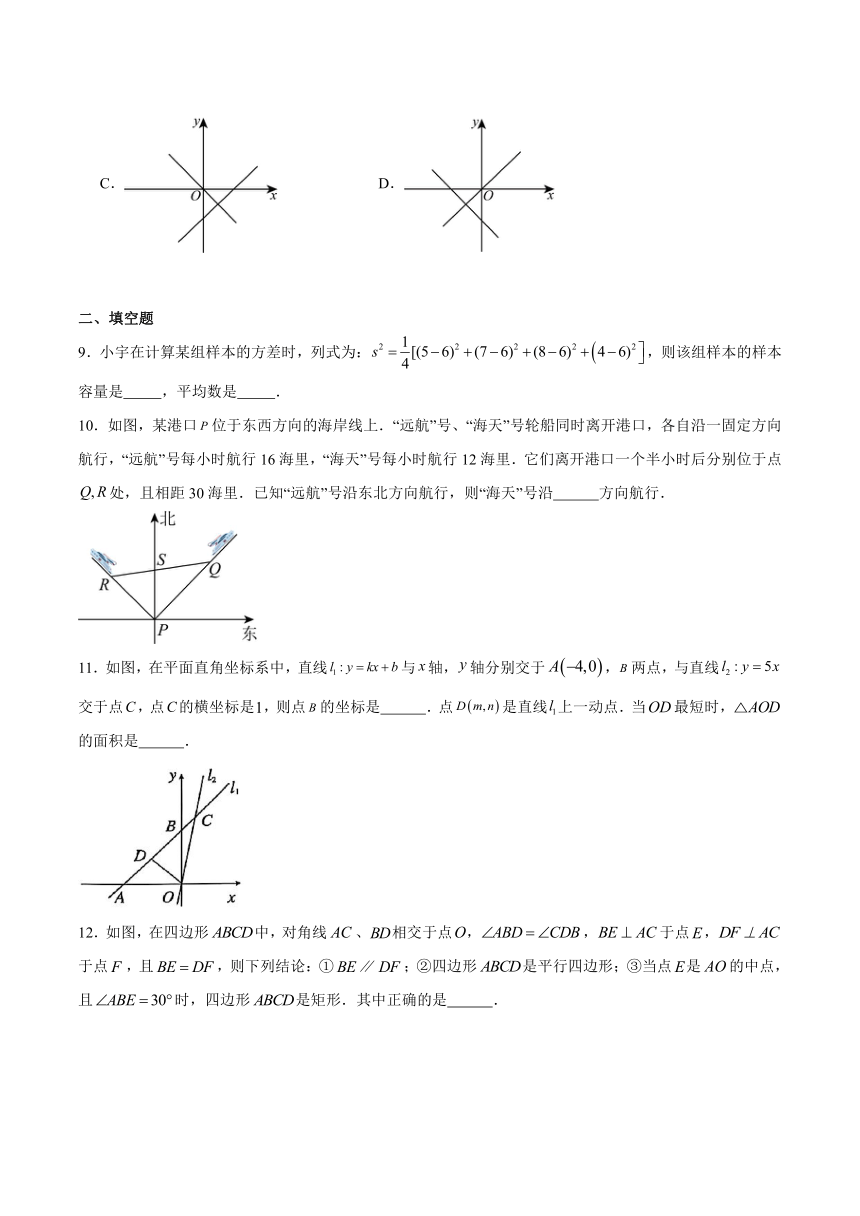
7.如图,在矩形纸片中,,点是边上一点,先将沿折叠,使得点落在点处,与交于点;再折叠矩形纸片,使得点与点重合,点落在点处,折痕为,则的面积是( )
A.10 B.8 C.12 D.
8.如图,在同一平面直角坐标系中,一次函数和一次函数的图象可能是( )
A. B.
C. D.
二、填空题
9.小宇在计算某组样本的方差时,列式为:,则该组样本的样本容量是 ,平均数是 .
10.如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点处,且相距30海里.已知“远航”号沿东北方向航行,则“海天”号沿 方向航行.
11.如图,在平面直角坐标系中,直线与轴,轴分别交于,两点,与直线交于点,点的横坐标是,则点的坐标是 .点是直线上一动点.当最短时,的面积是 .
12.如图,在四边形中,对角线、相交于点,,于点,于点,且,则下列结论:①;②四边形是平行四边形;③当点是的中点,且时,四边形是矩形.其中正确的是 .
三、解答题
13.计算:
(1);
(2);
(3)已知,,求的值.
14.为切实提升学生体质健康水平,某校开展学生体育综合素质测评工作.学校从七、八年级学生群体中,采用随机抽样的方式,各抽取80名学生的测评成绩(成绩以百分制计分),随后对抽样数据进行整理、描述和分析,下面给出了部分信息.
a.七年级80名学生测评成绩的频数分布直方图(数据分成6组:,,,,,)如图所示:
b.七年级80名学生测评成绩在这一组的是71,72,72,73,74,74,75,76,76,77,77,77,77,78,78,79,79,79.
c.七、八年级80名学生测评成绩的平均数、中位数和众数如表所示:
年级 平均数 中位数 众数
七年级 74.3 m 81
八年级 75 79 78
根据以上信息,回答下列问题.
(1)表中m的值是___________,并补全频数分布直方图.
(2)八年级小乐同学的测评成绩是77分,他的成绩高于本年级测评成绩的平均水平,所以他认为自己的成绩高于本年级一半以上学生的成绩.请判断他的说法是否正确,并说明理由.
(3)若该校七年级共有560名学生,测试的成绩60分及以上为合格,请你估计该校七年级学生测评成绩的合格人数.
15.在人教版八年级下册数学教材“测量学校旗杆高度”的数学活动里,聪聪设计了一种新颖的测量方法.从点C观察旗杆顶端的仰角为,接着往前走10米到达点D,观察旗杆顶端的仰角为.
(1)直接写出与的数量关系;
(2)根据聪聪的方法请你求出旗杆的高度.(人的身高忽略不计,结果保留根号)
16.如图,在中,对角线交于点,过点作于点,延长至点,使,连接.
(1)求证:四边形是矩形;
(2)若,,,求的面积.
17.“中国乳都”呼和浩特,以乳业为发展引擎,凭借优质乳业书写城市传奇、铸就辉煌.其中酸奶是深受大众喜爱的乳制饮品之一.某超市销售甲、乙两种品牌酸奶,结合以下材料解决问题.
内容
材料一 某超市销售甲、乙两种品牌的酸奶,甲种酸奶的进价为8元/罐;乙种酸奶的进货总金额(单位:元)与进货量(单位:罐)之间的关系如图所示,经过试销,甲、乙两种品牌酸奶的销售价分别为12元/罐和15元/罐.
材料二 某日,该超市销售甲、乙两种品牌的酸奶共800罐,其中乙种品牌的销售量不低于150罐,且不高于400罐.
任务一 (1)根据图像求出与的函数关系式.
任务二 (2)若购进的两种酸奶全部售完,设销售完甲、乙两种品牌的酸奶所获得的总利润为元,求出(单位:元)与乙种品牌酸奶的进货量(单位:罐)之间的函数关系式,并为该超市设计出获得最大利润的销售方案.
18.【课本再现】
如图1,正方形的对角线相交于点,点又是正方形的一个顶点,而且这两个正方形的边长相等,四边形为两个正方形的重叠部分,正方形可绕点转动.
【问题发现】
(1)①线段之间的数量关系是_______________;
②在①的基础上,连接,则线段之间的数量关系是____________.
【拓展应用】
(2)如图2,若矩形的一个顶点是矩形对角线的中点,与边相交于点,延长交于点,与边相交于点,连接.矩形可绕点转动,猜想之间的数量关系,并进行证明.
【类比迁移】
(3)如图3,在中,,点在边的中点处,它的两条边和分别与直线相交于点.可绕点转动,当时,请直接写出的面积.
参考答案
1.C
解:A:被开方数为负数,在实数范围内无意义,不是二次根式;
B:根指数为3,属于三次根式,不符合二次根式的定义;
C:根指数为2,且被开方数恒大于0(无论取何值),满足二次根式的条件;
D:根指数为2,但被开方数需满足才有意义,由于题目未限定的范围,无法保证其恒为非负数,因此不能直接判定为二次根式;
故选:C.
2.A
解:∵,
∴该三角形是直角三角形,
故选:A.
3.C
解:∵四边形是平行四边形,
∴,
∵是中点,
∴,
∴,
故选:C.
4.C
解:①新能源汽车电池充满电后,使用智能驾驶功能匀速耗电,则电池剩余电量y随使用时间x的增加而减小,符合题意;
②用长度一定的绳子围成一个矩形,周长一定时,矩形面积是长x的二次函数,不符合题意;
③点燃一根粗细均匀的蜡烛,蜡烛的剩余高度y与随燃烧时间x的增加而减小,符合题意;
故选:C.
5.D
解:由图可知德、智、体、美、劳的得分分别为、、、、,权重分别为、、、、.
总权重为.
根据加权平均数公式,最终得分
故选:D .
6.D
解:由表格可知,的值随值的增大而增大,故选项B错误;
∴,
当时,,
∴该函数的图像经过第一、二、三象限,故选项A错误;
当时,,故关于的方程的解不是,故选项C错误;
∵的值随值的增大而增大,且当时,,
∴不等式的解集为;故选项D正确;
故选:D.
7.A
解:∵四边形为矩形,
,
由折叠的性质可得:,,
,
∴、、在同一直线上,
,
设,则,
由勾股定理可得,即,
解得:,即,
,
,
,
,
,
则的面积是,
故选:A.
8.B
解:当时,图象经过一三四象限,经过一三象限,此时4个选项均不符合题意;
当时,图象经过一二三象限,经过二四象限,此时B选项符合题意.
故选:B.
9. 4 6
解:方差公式中的求和项:共有4个数据项,
分别为,每个数据点对应一个样本,
样本容量为4,
方差公式中的每个数据点均减去同一个数(即平均数),
根据公式,每个数据点被减去的数为6,
平均数.
故答案为:4,6.
10.西北方向
解:由题知,海里,海里,海里,,
,
,
是直角三角形,且,
,
“海天”号沿西北方向航行.
故答案为:西北方向
11. 4
解:把代入得到,,
∴
把,代入得到,
,
解得
∴直线,
当时,,
∴点的坐标是,
在中,,
∴
当最短,即时,
则
即,
∴,
∴的面积是
故答案为:,4
12.①②③
∵,
∴,
∴,
∵于点E,于点F,
∴,
∴,
故①正确.
∵,
∴,
∴,
∴四边形是平行四边形;
故②正确.
∵,点是的中点,,
∴是的垂直平分线,
∴,
∴,
∴是等边三角形,
∴,
∵四边形是平行四边形,
∴,,
∴,
∴四边形是矩形.故③正确.
故答案为:①②③.
13.(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
当,时,
原式
14.(1)77,图见解析
(2)不正确,理由见解析
(3)462人
(1)解:七年级这一组的频数为,
将七年级这80名学生的成绩从小到大排列处40位和41位两个数的平均数为,
即中位数,
补全频数分布直方图如图所示:
(2)解∶ 小乐的说法不正确,
因为抽取的八年级学生测评成绩的样本中位数为79分,可以估计,在这次体育综合素质测评工作中,八年级大约有一半学生的测评成绩高于79分,一半学生的测评成绩低于79分.
小乐的测评成绩为77分,低于中位数79分,可以推测他的成绩低于本年级一半以上学生的成绩,因此他的说法不正确.
(3)解: (人),
答:据估计该校七年级学生测评成绩的合格人数约为462人.
15.(1)
(2)米
(1)解:由题意及图,得
∴,,
∴
∴,
∴.
(2)由(1)知,米,
∴,
在中,
(米)
答:旗杆的高度为米.
16.(1)证明见解析
(2)
(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴,即,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是矩形,
∴,,
在中,由勾股定理得:,
∵,
∴,
∴,
解得,
∴,
∵,
∴.
17.(1)(2),甲品牌酸奶的进货量为400罐,乙品牌酸奶的进货量为400罐时,获得的利润最大
解:(1)依题意,设与的函数表达式为,
把代入解析式,
得,
∴与的函数表达式为;
(2)依题意,乙品牌酸奶的进货量罐,则甲品牌酸奶的进货量罐,
∵乙品牌的收购量不低于150罐,且不高于400罐,
∴,
由(1)得,
则,
∵,
∴随的增大而增大,
∵,
∴当时,最大,最大值为元,
(罐),
即甲品牌酸奶的进货量为罐,乙品牌酸奶的进货量为罐时,获得的利润最大.
18.(1)①②(2),证明见解析(3)或
解:(1)①证明:∵四边形是正方形,
∴,,
∴,
∴,
在和中,
,
∴,
∴;
②解:∵,
∴,
∴,
∴,
∵,,
∴,
∴,
故答案为:;
(2)解:;理由如下:
连接,如图2:
∵为矩形中心,
∴,
延长交于,
∵,
∴,
又,
∴,
∴,
又∵四边形是矩形,
∴,
∴垂直平分,
∴,
在中,由勾股定理得:,
∴;
(3)设,
①当在线段上时,如图3,
∵,
∴,
在中,,
∴,
∴,
又由(2)易知,
∴,
∴,
解得,即,
;
②当点在延长线上时,
同理可证,
∴,
又在中,
,
∴,
解得,即,
;
故的面积为或.
一、单选题
1.下列式子是二次根式的是( )
A. B. C. D.
2.已知某三角形的三条边长依次为,则该三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰三角形
3.如图,的对角线,相交于点O,点E是的中点,且,则的长是( )
A.5 B. C.10 D.15
4.下面的三个问题中都有两个变量:
①新能源汽车电池充满电后,使用智能驾驶功能匀速耗电,电池剩余电量与使用时间;
②用固定长度的新型导热线型材料,制作矩形形状的芯片散热框架,矩形面积与一边长;
③点燃一根粗细均匀的蜡烛,蜡烛的剩余高度与燃烧时间.
其中,变量与变量之间的函数关系可以用如图所示的图象表示的是( )
A.①② B.②③ C.①③ D.①②③
5.某校在学生期末评优工作中,全面贯彻“五育并举”理念,以德智体美劳全面发展为核心标准,依据的权重配比,对学生德、智、体、美、劳五个维度进行量化评分,综合评定学生的最终成绩.小鱼同学本学期这五方面的得分情况如图所示,则小鱼同学期末评优的最终得分是( )
A.9.1 B.9.2 C.9.3 D.9.4
6.已知一次函数,其中与的部分对应值如下表所示,根据该表提供的信息,下列说法正确的是( )
… 0 1 3 …
… 1 5 13 …
A.该函数的图像经过第一、三、四象限
B.函数值随值的增大而减小
C.关于的方程的解是
D.关于的不等式的解集为
7.如图,在矩形纸片中,,点是边上一点,先将沿折叠,使得点落在点处,与交于点;再折叠矩形纸片,使得点与点重合,点落在点处,折痕为,则的面积是( )
A.10 B.8 C.12 D.
8.如图,在同一平面直角坐标系中,一次函数和一次函数的图象可能是( )
A. B.
C. D.
二、填空题
9.小宇在计算某组样本的方差时,列式为:,则该组样本的样本容量是 ,平均数是 .
10.如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点处,且相距30海里.已知“远航”号沿东北方向航行,则“海天”号沿 方向航行.
11.如图,在平面直角坐标系中,直线与轴,轴分别交于,两点,与直线交于点,点的横坐标是,则点的坐标是 .点是直线上一动点.当最短时,的面积是 .
12.如图,在四边形中,对角线、相交于点,,于点,于点,且,则下列结论:①;②四边形是平行四边形;③当点是的中点,且时,四边形是矩形.其中正确的是 .
三、解答题
13.计算:
(1);
(2);
(3)已知,,求的值.
14.为切实提升学生体质健康水平,某校开展学生体育综合素质测评工作.学校从七、八年级学生群体中,采用随机抽样的方式,各抽取80名学生的测评成绩(成绩以百分制计分),随后对抽样数据进行整理、描述和分析,下面给出了部分信息.
a.七年级80名学生测评成绩的频数分布直方图(数据分成6组:,,,,,)如图所示:
b.七年级80名学生测评成绩在这一组的是71,72,72,73,74,74,75,76,76,77,77,77,77,78,78,79,79,79.
c.七、八年级80名学生测评成绩的平均数、中位数和众数如表所示:
年级 平均数 中位数 众数
七年级 74.3 m 81
八年级 75 79 78
根据以上信息,回答下列问题.
(1)表中m的值是___________,并补全频数分布直方图.
(2)八年级小乐同学的测评成绩是77分,他的成绩高于本年级测评成绩的平均水平,所以他认为自己的成绩高于本年级一半以上学生的成绩.请判断他的说法是否正确,并说明理由.
(3)若该校七年级共有560名学生,测试的成绩60分及以上为合格,请你估计该校七年级学生测评成绩的合格人数.
15.在人教版八年级下册数学教材“测量学校旗杆高度”的数学活动里,聪聪设计了一种新颖的测量方法.从点C观察旗杆顶端的仰角为,接着往前走10米到达点D,观察旗杆顶端的仰角为.
(1)直接写出与的数量关系;
(2)根据聪聪的方法请你求出旗杆的高度.(人的身高忽略不计,结果保留根号)
16.如图,在中,对角线交于点,过点作于点,延长至点,使,连接.
(1)求证:四边形是矩形;
(2)若,,,求的面积.
17.“中国乳都”呼和浩特,以乳业为发展引擎,凭借优质乳业书写城市传奇、铸就辉煌.其中酸奶是深受大众喜爱的乳制饮品之一.某超市销售甲、乙两种品牌酸奶,结合以下材料解决问题.
内容
材料一 某超市销售甲、乙两种品牌的酸奶,甲种酸奶的进价为8元/罐;乙种酸奶的进货总金额(单位:元)与进货量(单位:罐)之间的关系如图所示,经过试销,甲、乙两种品牌酸奶的销售价分别为12元/罐和15元/罐.
材料二 某日,该超市销售甲、乙两种品牌的酸奶共800罐,其中乙种品牌的销售量不低于150罐,且不高于400罐.
任务一 (1)根据图像求出与的函数关系式.
任务二 (2)若购进的两种酸奶全部售完,设销售完甲、乙两种品牌的酸奶所获得的总利润为元,求出(单位:元)与乙种品牌酸奶的进货量(单位:罐)之间的函数关系式,并为该超市设计出获得最大利润的销售方案.
18.【课本再现】
如图1,正方形的对角线相交于点,点又是正方形的一个顶点,而且这两个正方形的边长相等,四边形为两个正方形的重叠部分,正方形可绕点转动.
【问题发现】
(1)①线段之间的数量关系是_______________;
②在①的基础上,连接,则线段之间的数量关系是____________.
【拓展应用】
(2)如图2,若矩形的一个顶点是矩形对角线的中点,与边相交于点,延长交于点,与边相交于点,连接.矩形可绕点转动,猜想之间的数量关系,并进行证明.
【类比迁移】
(3)如图3,在中,,点在边的中点处,它的两条边和分别与直线相交于点.可绕点转动,当时,请直接写出的面积.
参考答案
1.C
解:A:被开方数为负数,在实数范围内无意义,不是二次根式;
B:根指数为3,属于三次根式,不符合二次根式的定义;
C:根指数为2,且被开方数恒大于0(无论取何值),满足二次根式的条件;
D:根指数为2,但被开方数需满足才有意义,由于题目未限定的范围,无法保证其恒为非负数,因此不能直接判定为二次根式;
故选:C.
2.A
解:∵,
∴该三角形是直角三角形,
故选:A.
3.C
解:∵四边形是平行四边形,
∴,
∵是中点,
∴,
∴,
故选:C.
4.C
解:①新能源汽车电池充满电后,使用智能驾驶功能匀速耗电,则电池剩余电量y随使用时间x的增加而减小,符合题意;
②用长度一定的绳子围成一个矩形,周长一定时,矩形面积是长x的二次函数,不符合题意;
③点燃一根粗细均匀的蜡烛,蜡烛的剩余高度y与随燃烧时间x的增加而减小,符合题意;
故选:C.
5.D
解:由图可知德、智、体、美、劳的得分分别为、、、、,权重分别为、、、、.
总权重为.
根据加权平均数公式,最终得分
故选:D .
6.D
解:由表格可知,的值随值的增大而增大,故选项B错误;
∴,
当时,,
∴该函数的图像经过第一、二、三象限,故选项A错误;
当时,,故关于的方程的解不是,故选项C错误;
∵的值随值的增大而增大,且当时,,
∴不等式的解集为;故选项D正确;
故选:D.
7.A
解:∵四边形为矩形,
,
由折叠的性质可得:,,
,
∴、、在同一直线上,
,
设,则,
由勾股定理可得,即,
解得:,即,
,
,
,
,
,
则的面积是,
故选:A.
8.B
解:当时,图象经过一三四象限,经过一三象限,此时4个选项均不符合题意;
当时,图象经过一二三象限,经过二四象限,此时B选项符合题意.
故选:B.
9. 4 6
解:方差公式中的求和项:共有4个数据项,
分别为,每个数据点对应一个样本,
样本容量为4,
方差公式中的每个数据点均减去同一个数(即平均数),
根据公式,每个数据点被减去的数为6,
平均数.
故答案为:4,6.
10.西北方向
解:由题知,海里,海里,海里,,
,
,
是直角三角形,且,
,
“海天”号沿西北方向航行.
故答案为:西北方向
11. 4
解:把代入得到,,
∴
把,代入得到,
,
解得
∴直线,
当时,,
∴点的坐标是,
在中,,
∴
当最短,即时,
则
即,
∴,
∴的面积是
故答案为:,4
12.①②③
∵,
∴,
∴,
∵于点E,于点F,
∴,
∴,
故①正确.
∵,
∴,
∴,
∴四边形是平行四边形;
故②正确.
∵,点是的中点,,
∴是的垂直平分线,
∴,
∴,
∴是等边三角形,
∴,
∵四边形是平行四边形,
∴,,
∴,
∴四边形是矩形.故③正确.
故答案为:①②③.
13.(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
当,时,
原式
14.(1)77,图见解析
(2)不正确,理由见解析
(3)462人
(1)解:七年级这一组的频数为,
将七年级这80名学生的成绩从小到大排列处40位和41位两个数的平均数为,
即中位数,
补全频数分布直方图如图所示:
(2)解∶ 小乐的说法不正确,
因为抽取的八年级学生测评成绩的样本中位数为79分,可以估计,在这次体育综合素质测评工作中,八年级大约有一半学生的测评成绩高于79分,一半学生的测评成绩低于79分.
小乐的测评成绩为77分,低于中位数79分,可以推测他的成绩低于本年级一半以上学生的成绩,因此他的说法不正确.
(3)解: (人),
答:据估计该校七年级学生测评成绩的合格人数约为462人.
15.(1)
(2)米
(1)解:由题意及图,得
∴,,
∴
∴,
∴.
(2)由(1)知,米,
∴,
在中,
(米)
答:旗杆的高度为米.
16.(1)证明见解析
(2)
(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵,
∴,即,
∴,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是矩形,
∴,,
在中,由勾股定理得:,
∵,
∴,
∴,
解得,
∴,
∵,
∴.
17.(1)(2),甲品牌酸奶的进货量为400罐,乙品牌酸奶的进货量为400罐时,获得的利润最大
解:(1)依题意,设与的函数表达式为,
把代入解析式,
得,
∴与的函数表达式为;
(2)依题意,乙品牌酸奶的进货量罐,则甲品牌酸奶的进货量罐,
∵乙品牌的收购量不低于150罐,且不高于400罐,
∴,
由(1)得,
则,
∵,
∴随的增大而增大,
∵,
∴当时,最大,最大值为元,
(罐),
即甲品牌酸奶的进货量为罐,乙品牌酸奶的进货量为罐时,获得的利润最大.
18.(1)①②(2),证明见解析(3)或
解:(1)①证明:∵四边形是正方形,
∴,,
∴,
∴,
在和中,
,
∴,
∴;
②解:∵,
∴,
∴,
∴,
∵,,
∴,
∴,
故答案为:;
(2)解:;理由如下:
连接,如图2:
∵为矩形中心,
∴,
延长交于,
∵,
∴,
又,
∴,
∴,
又∵四边形是矩形,
∴,
∴垂直平分,
∴,
在中,由勾股定理得:,
∴;
(3)设,
①当在线段上时,如图3,
∵,
∴,
在中,,
∴,
∴,
又由(2)易知,
∴,
∴,
解得,即,
;
②当点在延长线上时,
同理可证,
∴,
又在中,
,
∴,
解得,即,
;
故的面积为或.
同课章节目录
