2026年中考数学复习课件 专题五 四边形-第23讲 多边形与平行四边形(共51张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题五 四边形-第23讲 多边形与平行四边形(共51张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 21:06:46 | ||
图片预览






文档简介
(共51张PPT)
复习讲义
第一篇 考点精讲
专题五 四边形
图1
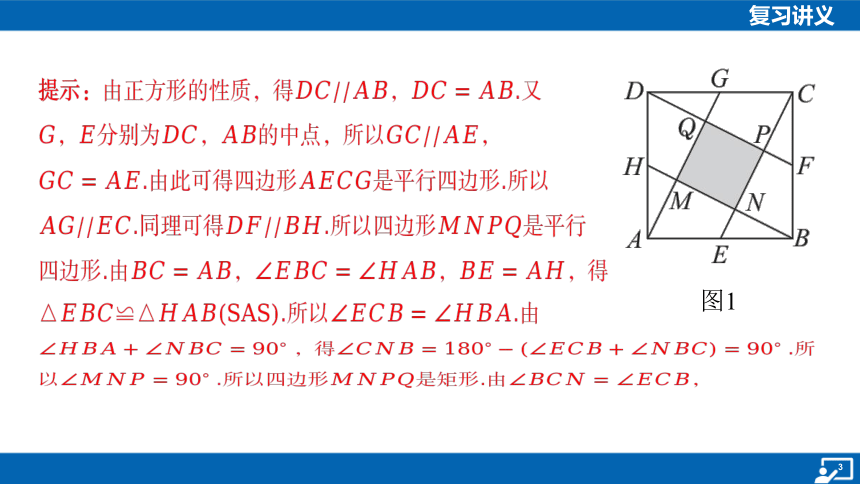
1.(2024·广西·中考第12题)如图1,正方形 的
边长为5,,,,分别为各边中点.连接 ,
,,,交点分别为,,, ,则四边
形 的面积为( ).
A.1 B.2 C.5 D.10
图1
提示:由正方形的性质,得, .又
,分别为,的中点,所以 ,
.由此可得四边形 是平行四边形.所以
.同理可得.所以四边形 是平行
四边形.由,, ,得
.所以 .由
,得 .所
以 .所以四边形是矩形.由 ,
,得.所以 ,
即 .同理可得
.由,得 .
所以 .同理可得
.故四边形 的面积为
.
【答案】C
图1
2.(2024·广西·中考第17题)如图2,两张宽度均为 的纸条交叉叠放
在一起,交叉形成的锐角为 ,则重合部分构成的四边形 的周
长为_____ .
图2
提示:如图29,过点作于点, 于点,则 . .由题意可知,四边形 为平行四边形,, 所以.由此可得,四边形 为菱形.故四边形的周长为 .
图29
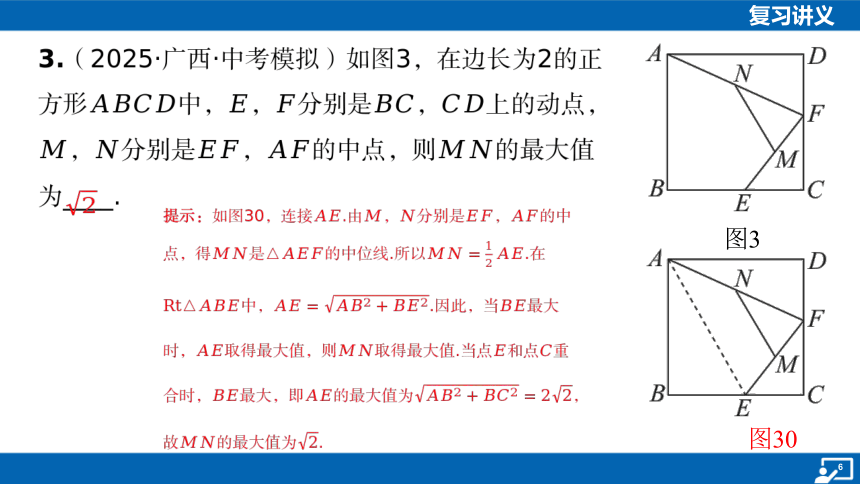
3.(2025·广西·中考模拟)如图3,在边长为2的正方形中, ,分别是,上的动点,,分别是,的中点,则 的最大值为____.
图3
图30
提示:如图30,连接.由,分别是, 的中
点,得是的中位线.所以 .在
中,.因此,当 最大
时,取得最大值,则取得最大值.当点和点 重
合时,最大,即的最大值为 ,
故的最大值为 .
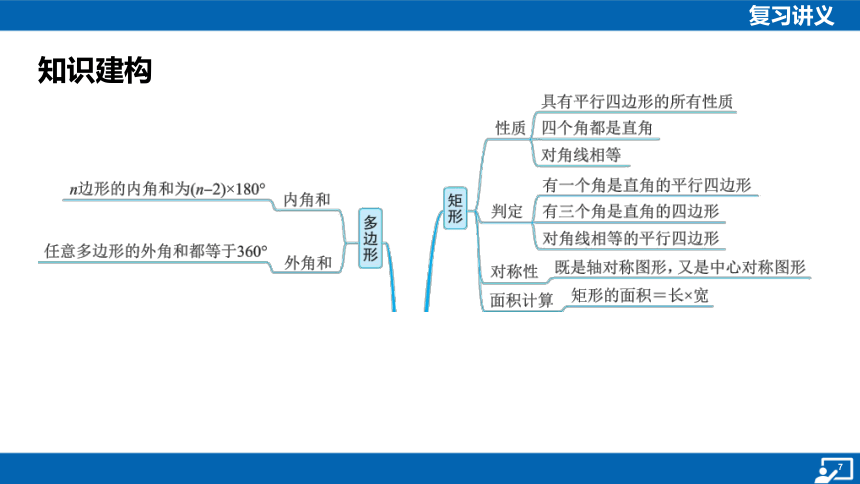
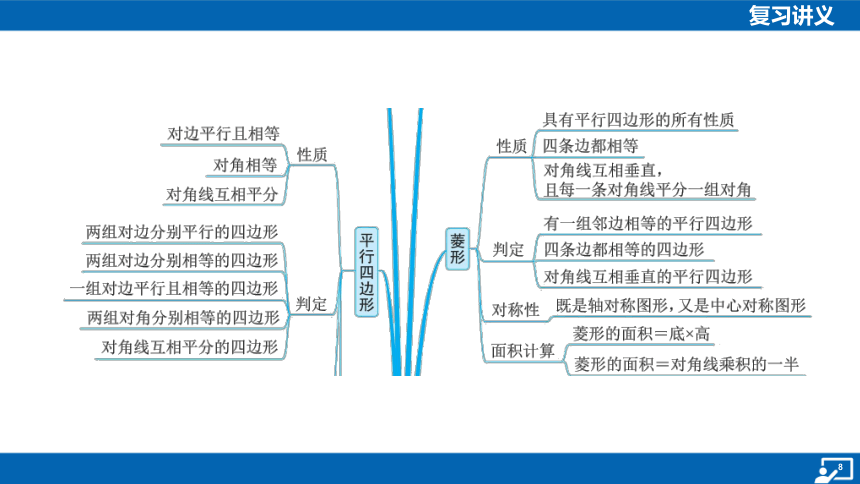
知识建构
第23讲 多边形与平行四边形
聚焦核心
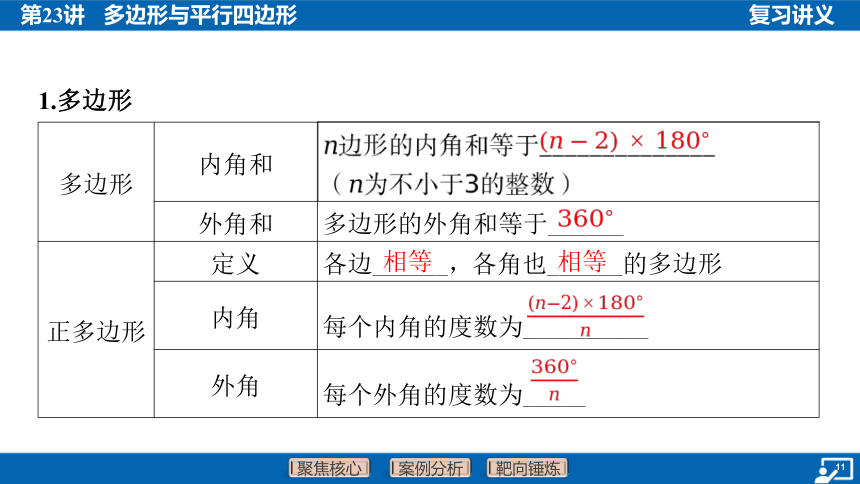
1.多边形
多边形 内角和
外角和 多边形的外角和等于______
正多边形 定义 各边______,各角也______的多边形
内角 每个内角的度数为_ _________
外角 每个外角的度数为_ ____
相等
相等
2.平行四边形
平行四边形 __________________________________________ 定义 两组对边分别______的四边形叫作平行四边形
性质 边:对边______且______
角:对角______
对角线:对角线互相______
对称性:平行四边形是______对称图形,它的
对称中心是两条________的交点
平行
平行
相等
相等
平分
中心
对角线
平行四边形 __________________________________________ 判定
平行
相等
续表
平行四边形 __________________________________________ 判定
平行
相等
相等
续表
平行四边形 __________________________________________ 判定
周长
面积
平分
续表
第23讲 多边形与平行四边形
案例分析
考点一 多边形的相关计算
名师指导 当已知多边形的边数求多边形的内角和,或已知多边形的内
角和求多边形的边数时,可直接运用多边形的内角和公式求解;当已知
正多边形的一个外角(或内角)时,运用多边形的外角和为 来计
算比较简便.
例1 (2024·四川遂宁·中考)佩佩在“黄娥古镇”研学时学习扎染技术,
得到的扎染图案是一个内角和为 的正多边形,这个正多边形的
每个外角为( ).
A. B. C. D.
提示:设这个正多边形的边数为.由题意,得 .
解得.又 ,故这个正多边形的每个外角为 .
C
思路点拨 设这个正多边形的边数为,利用多边形的内角和公式求得
的值,再利用多边形的外角和为 列式计算.
考点专练
1.(2024·四川乐山·中考)下列多边形中,内角和最小的是( ).
A
A. B. C. D.
2.(2025·甘肃临夏·中考改编)“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂
的外边框为正六边形(如图2),则该正六边形的每个内角的度数为
______.
图1
图2
考点二 平行四边形的性质
名师指导
1.平行四边形的每条对角线把它分成两个全等的三角形,两条对角
线把平行四边形分成四组全等的三角形.
2.在解决平行四边形中的线段或角相等的问题时,常利用平行四边
形的性质证明三角形全等来解决.
3.过平行四边形的中心(对角线的交点)的任意一条直线将平行四
边形的面积等分.
图3
例2 (2025·广西南宁·模拟)如图3,在
中,,平分,交于点,过点
作于点,交于点.若,则
的长为( ).
A.8 B.10 C.12 D.16
思路点拨 由平行四边形的性质,可知 ,则求出的长即可得到的长.已知 的长,且图中有角平分线,则考虑结合平行线的性质、“等角对等边”,将线段等量代换,最后求得结果.
图3
提示:因为平分,所以 .由
平行四边形的性质,得, ,
, .所以
.从而得 .所以
【答案】C
.由,得.因为 ,所以
.又 , .所以
.从而得.所以 .
故 .
考点专练
图4
3.(2024·四川眉山·中考)如图4,在 中,点
是的中点,过点 ,有下列结论:
,, ,
.其中正确结论的个数为
( ).
C
A.1个 B.2个 C.3个 D.4个
图5
4.(2025·山东菏泽·中考模拟)如图5,在 中,
平分,交于点,平分 ,交
于点.求证: .
证明: 四边形是平行四边形, ,,
平分,平分, .
在和中,, ,,
.
考点三 平行四边形的判定
名师指导 证明一个四边形是平行四边形的基本思路:
(1)若已知一组对边平行,则可以证明这组对边相等,或另一组
对边平行;
(2)若已知一组对边相等,则可以证明这组对边平行,或另一组
对边相等;
(3)若已知条件与对角线有关,则可以证明对角线互相平分.
图6
例3 (2024·北京·中考)如图6,在四边形
中,是的中点,,相交于点 ,
, .
(1)求证:四边形 为平行四边形.
证明: ,即是的中点,又 是的中点, 是
的中位线.
,即.
又 , 四边形 为平行四边形.
思路点拨(1)已知 ,且已知条件中无线段长,则考虑证明另一组对边平行,即可证明四边形 为平行四边形.
(2)已知 ,,,求 的长.
图6
解:由(1)知,是的中位线,
四边形为平行四边形,
,,
,
.
思路点拨 (2)由 ,可知, 是直角三角形,则可根据三角函数和勾股定理求出相应的线段的长.
思路点拨(1)已知 ,且已知条件中无线段长,则考虑证明另一
组对边平行,即可证明四边形 为平行四边形. 思路点拨 (2)由
,可知, 是直角三角形,则可根据三角函数
和勾股定理求出相应的线段的长.
图6
考点专练
图7
5.(2024·辽宁·中考)如图7, 的对角线
,相交于点,, .若
,,则四边形 的周长为
( ).
A.4 B.6 C.8 D.16
提示:由平行四边形的性质,得 ,.由
, ,得四边形是平行四边形.故四边形 的周长= .
C
6.(2024·山东济宁·中考)如图8,四边形的对角线, 相交于
点,已知 ,请补充一个条件_____________________________
____________________________ ,使四边形 是平行四边形.
或或(答案不唯一,写出一个即可)
图8
图9
7.(2024·湖南·中考)如图9,在四边形 中,
,点在边 上,________.请从“;, ”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 为平行四边形.
解:选择①,证明: , .
又 ,即, 四边形为平行四边形.
选择②,证明: ,, .
又 ,即 , 四边形 为平行四边形.
(2)已知,,,求线段 的长.
图9
解:由(1)可知,四边形为平行四边形,
, .
.
第23讲 多边形与平行四边形
靶向锤炼
靶向练
1.(2025·广西南宁·模拟)正五边形的外角和为( ).
C
A. B. C. D.
图1
2.传统文化 我国古代建筑具有悠久的历史和光辉的成就,其
建筑艺术也是美术鉴赏的重要对象.图1是我国古代建筑中的一
个正八边形窗户,则它的内角和为( ).
A
A. B. C. D.
3.(2024·贵州·中考)如图2,的对角线与相交于点 ,则
下列结论一定正确的是( ).
B
图2
A. B. C. D.
4.(2024·四川乐山·中考)如图3,下列条件中,不能判定四边形
为平行四边形的是( ).
D
图3
A.,
B.,
C.,
D.,
图4
5.(2025·四川泸州·中考模拟)如图4, 的对
角线,相交于点, 的平分线与边
相交于点,是的中点.若 ,
,则 的长为( ).
A
A.1 B.2 C.3 D.4
6.(2024·四川巴中·中考)从五边形的一个顶点出发可以引___条对角线.
2
图5
7.(2025·四川凉山·中考模拟)如图5,在平面直角坐标
系中,的顶点,,的坐标分别是 ,
,,则顶点 的坐标是______.
8.(2024·湖北·中考)如图6,在中,,是对角线 上的两点,
且,求证: .
图6
解: 四边形是平行四边形, ,
.
在和中,, ,,
.
图7
9.如图7,在四边形中, ,
,, .
(1)求证:四边形 是平行四边形.
证明: ,, ,
, .
又 , 四边形 是平行四边形.
图7
(2)求的长和四边形 的面积.
解: 四边形是平行四边形,
,,∴ .
攻坚练
图8
10.(2024·河北·中考)如图8,直线 与正六边形
的边,分别相交于点,,则
等于( ).
A. B. C. D.
提示:正六边形每个内角为 ,六边
形的内角和为 ,即
,所以
.因为
,所以 .
图8
【答案】B
图9
11.(2024·山东·中考)如图9,为 的对
角线上一点,,,连接 并
延长至点,使得,连接,则 的
长为( ).
B
A. B.3 C. D.4
提示:连接,交于点,由平行四边形的性质,得 ,
.又,所以是 的中位线.故
.
图10
12.(2024·四川雅安·中考)如图10, 是
的对角线的交点,过点 的直线分别交
,于点, .
(1)求证: .
证明: 四边形是平行四边形,∴
是 的对角线的交点, .
在和 中,, ,, .
(2)当,时,分别连接,,求四边形
的周长.
图10
解: , .
又 , 四边形 是平行四边形.
, 四边形是菱形.
∴
四边形 的周长为4 .
拔尖练
图11
13.(2024·黑龙江大庆·中考)如图11,在
中,,分别是, 的平分
线,且点,分别在边, 上.
(1)求证:四边形 是平行四边形.
图11
证明: 四边形是平行四边形, ,
,分别是,的平分线, ,
.
又 , 四边形 是平行四边形.
(2)已知 ,,求 的面积.
图11
图44
解:如图44,过点作于点 ,则 .
四边形是平行四边形, , .
是的平分线, .
又 .
是等边三角形.
,.在 中,
由勾股定理,得.
.
由(1)可知四边形是平行四边形,∴
,∴
.
图44
复习讲义
第一篇 考点精讲
专题五 四边形
图1
1.(2024·广西·中考第12题)如图1,正方形 的
边长为5,,,,分别为各边中点.连接 ,
,,,交点分别为,,, ,则四边
形 的面积为( ).
A.1 B.2 C.5 D.10
图1
提示:由正方形的性质,得, .又
,分别为,的中点,所以 ,
.由此可得四边形 是平行四边形.所以
.同理可得.所以四边形 是平行
四边形.由,, ,得
.所以 .由
,得 .所
以 .所以四边形是矩形.由 ,
,得.所以 ,
即 .同理可得
.由,得 .
所以 .同理可得
.故四边形 的面积为
.
【答案】C
图1
2.(2024·广西·中考第17题)如图2,两张宽度均为 的纸条交叉叠放
在一起,交叉形成的锐角为 ,则重合部分构成的四边形 的周
长为_____ .
图2
提示:如图29,过点作于点, 于点,则 . .由题意可知,四边形 为平行四边形,, 所以.由此可得,四边形 为菱形.故四边形的周长为 .
图29
3.(2025·广西·中考模拟)如图3,在边长为2的正方形中, ,分别是,上的动点,,分别是,的中点,则 的最大值为____.
图3
图30
提示:如图30,连接.由,分别是, 的中
点,得是的中位线.所以 .在
中,.因此,当 最大
时,取得最大值,则取得最大值.当点和点 重
合时,最大,即的最大值为 ,
故的最大值为 .
知识建构
第23讲 多边形与平行四边形
聚焦核心
1.多边形
多边形 内角和
外角和 多边形的外角和等于______
正多边形 定义 各边______,各角也______的多边形
内角 每个内角的度数为_ _________
外角 每个外角的度数为_ ____
相等
相等
2.平行四边形
平行四边形 __________________________________________ 定义 两组对边分别______的四边形叫作平行四边形
性质 边:对边______且______
角:对角______
对角线:对角线互相______
对称性:平行四边形是______对称图形,它的
对称中心是两条________的交点
平行
平行
相等
相等
平分
中心
对角线
平行四边形 __________________________________________ 判定
平行
相等
续表
平行四边形 __________________________________________ 判定
平行
相等
相等
续表
平行四边形 __________________________________________ 判定
周长
面积
平分
续表
第23讲 多边形与平行四边形
案例分析
考点一 多边形的相关计算
名师指导 当已知多边形的边数求多边形的内角和,或已知多边形的内
角和求多边形的边数时,可直接运用多边形的内角和公式求解;当已知
正多边形的一个外角(或内角)时,运用多边形的外角和为 来计
算比较简便.
例1 (2024·四川遂宁·中考)佩佩在“黄娥古镇”研学时学习扎染技术,
得到的扎染图案是一个内角和为 的正多边形,这个正多边形的
每个外角为( ).
A. B. C. D.
提示:设这个正多边形的边数为.由题意,得 .
解得.又 ,故这个正多边形的每个外角为 .
C
思路点拨 设这个正多边形的边数为,利用多边形的内角和公式求得
的值,再利用多边形的外角和为 列式计算.
考点专练
1.(2024·四川乐山·中考)下列多边形中,内角和最小的是( ).
A
A. B. C. D.
2.(2025·甘肃临夏·中考改编)“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂
的外边框为正六边形(如图2),则该正六边形的每个内角的度数为
______.
图1
图2
考点二 平行四边形的性质
名师指导
1.平行四边形的每条对角线把它分成两个全等的三角形,两条对角
线把平行四边形分成四组全等的三角形.
2.在解决平行四边形中的线段或角相等的问题时,常利用平行四边
形的性质证明三角形全等来解决.
3.过平行四边形的中心(对角线的交点)的任意一条直线将平行四
边形的面积等分.
图3
例2 (2025·广西南宁·模拟)如图3,在
中,,平分,交于点,过点
作于点,交于点.若,则
的长为( ).
A.8 B.10 C.12 D.16
思路点拨 由平行四边形的性质,可知 ,则求出的长即可得到的长.已知 的长,且图中有角平分线,则考虑结合平行线的性质、“等角对等边”,将线段等量代换,最后求得结果.
图3
提示:因为平分,所以 .由
平行四边形的性质,得, ,
, .所以
.从而得 .所以
【答案】C
.由,得.因为 ,所以
.又 , .所以
.从而得.所以 .
故 .
考点专练
图4
3.(2024·四川眉山·中考)如图4,在 中,点
是的中点,过点 ,有下列结论:
,, ,
.其中正确结论的个数为
( ).
C
A.1个 B.2个 C.3个 D.4个
图5
4.(2025·山东菏泽·中考模拟)如图5,在 中,
平分,交于点,平分 ,交
于点.求证: .
证明: 四边形是平行四边形, ,,
平分,平分, .
在和中,, ,,
.
考点三 平行四边形的判定
名师指导 证明一个四边形是平行四边形的基本思路:
(1)若已知一组对边平行,则可以证明这组对边相等,或另一组
对边平行;
(2)若已知一组对边相等,则可以证明这组对边平行,或另一组
对边相等;
(3)若已知条件与对角线有关,则可以证明对角线互相平分.
图6
例3 (2024·北京·中考)如图6,在四边形
中,是的中点,,相交于点 ,
, .
(1)求证:四边形 为平行四边形.
证明: ,即是的中点,又 是的中点, 是
的中位线.
,即.
又 , 四边形 为平行四边形.
思路点拨(1)已知 ,且已知条件中无线段长,则考虑证明另一组对边平行,即可证明四边形 为平行四边形.
(2)已知 ,,,求 的长.
图6
解:由(1)知,是的中位线,
四边形为平行四边形,
,,
,
.
思路点拨 (2)由 ,可知, 是直角三角形,则可根据三角函数和勾股定理求出相应的线段的长.
思路点拨(1)已知 ,且已知条件中无线段长,则考虑证明另一
组对边平行,即可证明四边形 为平行四边形. 思路点拨 (2)由
,可知, 是直角三角形,则可根据三角函数
和勾股定理求出相应的线段的长.
图6
考点专练
图7
5.(2024·辽宁·中考)如图7, 的对角线
,相交于点,, .若
,,则四边形 的周长为
( ).
A.4 B.6 C.8 D.16
提示:由平行四边形的性质,得 ,.由
, ,得四边形是平行四边形.故四边形 的周长= .
C
6.(2024·山东济宁·中考)如图8,四边形的对角线, 相交于
点,已知 ,请补充一个条件_____________________________
____________________________ ,使四边形 是平行四边形.
或或(答案不唯一,写出一个即可)
图8
图9
7.(2024·湖南·中考)如图9,在四边形 中,
,点在边 上,________.请从“;, ”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 为平行四边形.
解:选择①,证明: , .
又 ,即, 四边形为平行四边形.
选择②,证明: ,, .
又 ,即 , 四边形 为平行四边形.
(2)已知,,,求线段 的长.
图9
解:由(1)可知,四边形为平行四边形,
, .
.
第23讲 多边形与平行四边形
靶向锤炼
靶向练
1.(2025·广西南宁·模拟)正五边形的外角和为( ).
C
A. B. C. D.
图1
2.传统文化 我国古代建筑具有悠久的历史和光辉的成就,其
建筑艺术也是美术鉴赏的重要对象.图1是我国古代建筑中的一
个正八边形窗户,则它的内角和为( ).
A
A. B. C. D.
3.(2024·贵州·中考)如图2,的对角线与相交于点 ,则
下列结论一定正确的是( ).
B
图2
A. B. C. D.
4.(2024·四川乐山·中考)如图3,下列条件中,不能判定四边形
为平行四边形的是( ).
D
图3
A.,
B.,
C.,
D.,
图4
5.(2025·四川泸州·中考模拟)如图4, 的对
角线,相交于点, 的平分线与边
相交于点,是的中点.若 ,
,则 的长为( ).
A
A.1 B.2 C.3 D.4
6.(2024·四川巴中·中考)从五边形的一个顶点出发可以引___条对角线.
2
图5
7.(2025·四川凉山·中考模拟)如图5,在平面直角坐标
系中,的顶点,,的坐标分别是 ,
,,则顶点 的坐标是______.
8.(2024·湖北·中考)如图6,在中,,是对角线 上的两点,
且,求证: .
图6
解: 四边形是平行四边形, ,
.
在和中,, ,,
.
图7
9.如图7,在四边形中, ,
,, .
(1)求证:四边形 是平行四边形.
证明: ,, ,
, .
又 , 四边形 是平行四边形.
图7
(2)求的长和四边形 的面积.
解: 四边形是平行四边形,
,,∴ .
攻坚练
图8
10.(2024·河北·中考)如图8,直线 与正六边形
的边,分别相交于点,,则
等于( ).
A. B. C. D.
提示:正六边形每个内角为 ,六边
形的内角和为 ,即
,所以
.因为
,所以 .
图8
【答案】B
图9
11.(2024·山东·中考)如图9,为 的对
角线上一点,,,连接 并
延长至点,使得,连接,则 的
长为( ).
B
A. B.3 C. D.4
提示:连接,交于点,由平行四边形的性质,得 ,
.又,所以是 的中位线.故
.
图10
12.(2024·四川雅安·中考)如图10, 是
的对角线的交点,过点 的直线分别交
,于点, .
(1)求证: .
证明: 四边形是平行四边形,∴
是 的对角线的交点, .
在和 中,, ,, .
(2)当,时,分别连接,,求四边形
的周长.
图10
解: , .
又 , 四边形 是平行四边形.
, 四边形是菱形.
∴
四边形 的周长为4 .
拔尖练
图11
13.(2024·黑龙江大庆·中考)如图11,在
中,,分别是, 的平分
线,且点,分别在边, 上.
(1)求证:四边形 是平行四边形.
图11
证明: 四边形是平行四边形, ,
,分别是,的平分线, ,
.
又 , 四边形 是平行四边形.
(2)已知 ,,求 的面积.
图11
图44
解:如图44,过点作于点 ,则 .
四边形是平行四边形, , .
是的平分线, .
又 .
是等边三角形.
,.在 中,
由勾股定理,得.
.
由(1)可知四边形是平行四边形,∴
,∴
.
图44
同课章节目录
