2026年中考数学复习课件 专题四 三角形-第21讲 相似三角形(共55张PPT)

(共55张PPT)
复习讲义
第一篇 考点精讲
专题四 三角形
第21讲 相似三角形
聚焦核心
1.相似多边形
比例线段
相似多边形 的有关概念 两个边数相同的多边形，如果它们的对应角______，对
应边________，那么这两个多边形叫作相似多边形.相似
多边形对应边的比叫作________
相等
成比例
相似比
相似多边形 的性质 相似多边形的对应角______，对应边________
相似多边形的周长比等于________，面积比等于______________
平行线分线 段 成比例 两条直线被一组平行线所截，所得的对应线段________
平行于三角形一边的直线截其他两边（或两边的延长
线），所得的对应线段________
相等
成比例
相似比
相似比的平方
成比例
成比例
续表
2.相似三角形
相关概 念 三个角分别______，三条边________的两个三角形叫作相似三角形.相似三角形对应边的比叫作________，相似比为1的两个三角形是______三角形
判定
图1
相等
成比例
相似比
全等
判定 两角分别______的两个三角形相似
两边________且______相等的两个三角形相似
三边________的两个三角形相似
如果一个直角三角形的斜边和一条直角边与另一个直角三角形
的斜边和一条直角边对应成比例，那么这两个直角三角形相似
相等
成比例
夹角
成比例
续表
性质 相似三角形的对应角______，对应边________
相似三角形对应高、对应中线、对应角平分线的比都等于
_________
相似三角形的周长比等于________，面积比等于____________
相等
成比例
相似比
相似比
相似比的平方
续表
第21讲 相似三角形
案例分析
考点一 平行线分线段成比例
名师指导
1.在平行线分线段成比例的基本事实中，一组平行线两两平行，被
截直线不一定平行．
2.所有的成比例线段是指被截直线上的线段，与这组平行线上的线
段无关，注意对应线段应写在对应位置上．
图2
例1 （2025·北京·中考模拟）如图2，直线， 交于点
，.若，， ，则
的值为__.
提示：因为，，所以 .由
，得 .
思路点拨 观察图形可发现，直线 被平行线所截形
成的线段是，，直线 被平行线所截形成的线
段是， ，根据平行线分线段成比例定理，可得
.
考点专练
图3
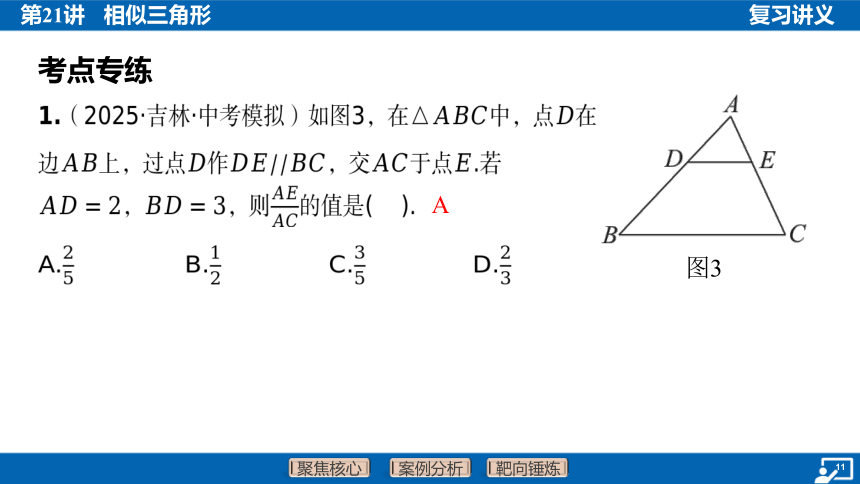
1.（2025·吉林·中考模拟）如图3，在中，点 在
边上，过点作，交于点 .若
，，则 的值是( ).
A
A. B. C. D.
图4
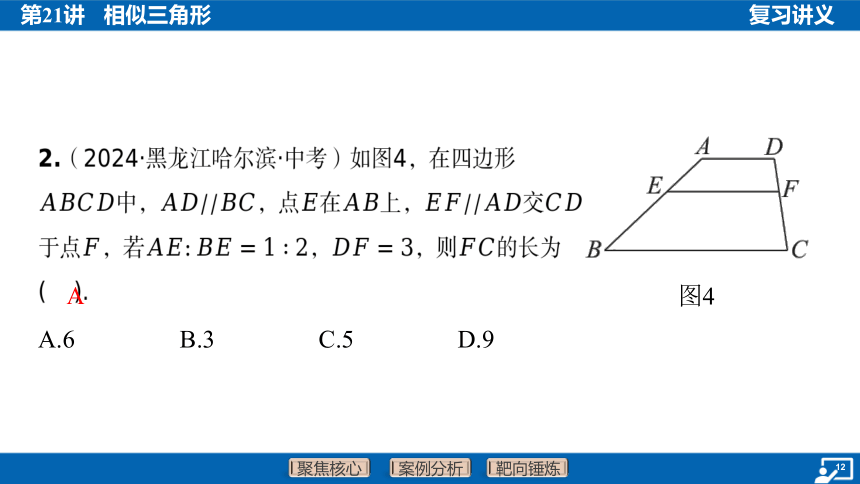
2.（2024·黑龙江哈尔滨·中考）如图4，在四边形
中，，点在上，交
于点，若，，则 的长为
( ).
A
A.6 B.3 C.5 D.9
考点二 相似三角形的判定
名师指导
1.判定相似三角形的一般思路：
（1）若已知条件中有平行线，则找“A”型图形或“”型图形；
（2）若已知有一组角相等，则找另一组角相等，或找夹该角的两
边对应成比例；
（3）若已知条件不能确定角相等，则找三角形的三边对应成比例.
2.在判定三角形相似时，要注意对公共边、公共角、对顶角等隐含
条件的挖掘.
图5
例2 （2025·湖南湘潭·中考改编）如图5，在
中， ，是斜边 上的
高.求证： .
证明： 是斜边上的高， .
， .
又 ， .
思路点拨 观察图形可发现，为 ， 的公共角，则再找一组角相等，即可证得 .
考点专练
3.（2025·黑龙江大庆·中考模拟）在综合与实践课上，老师组织同学们以“矩
形的折叠”为主题开展数学活动.如图6，有一张矩形纸片，点 在
边上，现将矩形折叠，折痕为，点对应的点记为点，若点 恰
好落在边上，则图6中与 一定相似的三角形是________.
图6
图7
4.（2024·广东广州·中考）如图7，点， 分别在正
方形的边，上，， ，
.
求证： .
证明： ，，
四边形是正方形， ， .
∵ ，， .
.
考点三 相似三角形的性质
名师指导
1.利用相似三角形对应角相等的性质可实现角之间的转化，为解决
其他问题提供条件.
2.相似三角形的对应边成比例反映出两个三角形中线段之间的等量
关系，常作为求线段长或线段长的比的方法.
图8
例3 （2024·湖南·中考）如图8，在中，， 分
别为边， 的中点.下列结论错误的是( ).
A. B.
C. D.
思路点拨 图中是一个“A”型图形，且由三角形中位线的性质可得
，.由此可得与 相似，并求得它们的相
似比，再根据相似三角形的性质即可解决问题.
图8
提示：由题意可知，是 的中位线，从而得，.故选项A，C不符合题意.由 ，得 .故选项B不符合题意.由相似三角形的性质，得 .由此可得
.故选项D符合题意.
答案：D
考点专练
5.（2024·云南·中考）如图9，与交于点，且 .若
，则 __.
图9
图10
6.（2024·上海·中考节选）如图10，在矩形 中，
为边上一点，且.求证： .
证明： 四边形是矩形， ，
.
，∴ .
. ，
，即 ， .
考点四 相似三角形的应用
名师指导
1.利用相似三角形的性质解决实际问题
2.测量宽度问题常见的模型
类型 模型图 相关算式
“A”型 ____________________________________________________
___________________________________________________ 类型 模型图 相关算式
___________________________________________________
续表
3.测量高度问题常见的模型
类型 模型图 相关算式
影长测量 _______________________________________________________
标杆测量 ________________________________________________________
类型 模型图 相关算式
反射测量 _______________________________________________________
续表
图11
例4 （2025·四川攀枝花·中考模拟）某
数学兴趣小组决定采用我国古代数
学家赵爽利用影子对物体进行测量
的原理，来测量一座塔的高度.图11
是测量方案的示意图，该塔的高度为，选取与塔底 在同一水平地面
上的，两点，分别垂直地面竖立两根高为的标杆和 ，两标
杆间隔为，并且塔、标杆和 在同一竖直平面内.从标杆
向右走到点处（即），从点处观察点，发现点 ，
，在同一直线上；从标杆向右走到点处（即 ），从
点处观察点，点，，三点也在同一直线上，且点，，，，
在同一直线上. 请你根据以上测量数据，帮助兴趣小组求出塔 的高度.
图11
解：设 ，则.
，，
，即 .
同理可证， ，即.
.解得 .
经检验，是原方程的解，且符合实际意义.
. .
答：塔的高度为 .
图11
思路点拨 标杆、塔都垂直于地面，是互
相平行的，由此可找到相似三角形.根据
标杆、塔的高度不变，可运用方程思想
列出方程求解.
考点专练
图12
7.（2025·四川南充·中考）如图12，数学活动课上，为测
量学校旗杆高度，小菲同学在脚下水平放置一块平面镜，
然后向后退（保持脚、镜和旗杆底端在同一直线上），直
到她刚好在平面镜中看到旗杆的顶端.已知小菲的眼睛距
A. B. C. D.
离地面，同时量得小菲与平面镜的水平距离为 ，平面镜与旗杆
的水平距离为 ，则旗杆高度为( ).
提示：由，，得 .
又 ， ，
即. .
图12
【答案】B
图13
8.（2025·江苏镇江·中考模拟）如图13，用一个卡钳
（，）测量某个零件的内孔直径 ，
量得长为，则____ .
18
提示：由， ，得
. .
第21讲 相似三角形
靶向锤炼
靶向练
1.（2024·重庆·中考）若两个相似三角形的相似比是 ，则这两个相似
三角形的面积比是( ).
D
A. B. C. D.
图1
2.（2025·广西柳州·模拟）如图1，已知 ，
，，则 的长为( ).
C
A.4 B.5 C.6 D.7
3.在研究相似问题时，甲、乙同学的观点如下：甲认为，将边长为3，4，
5的三角形按图2的方式向外扩张，得到新三角形，它们的对应边间距为
1，则新三角形与原三角形相似.乙认为，将邻边为3和5的矩形按图3的
方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与
原矩形不相似.对于两人的观点，下列说法正确的是( ).
A
图2
图3
A.两人都对 B.两人都不对 C.甲对，乙不对 D.甲不对，乙对
4.如图4，下列条件不能判定 的是( ).
C
图4
A.， B.
C.， D.，
图5
5.（2025·广西柳州·模拟）如图5，某数学兴趣小组为了
估算河的宽度，在河对岸选定一个目标点 ，在近岸取点
和，使点，，共线且直线 与河垂直，接着在过
点且与垂直的直线上选择适当的点，确定 与过
点且垂直的直线的交点.若测得 ，
，，则河的大致宽度 是( ).
A. B. C. D.
提示：根据题意，得.从而得 .所
以，即.解得 .
C
6.（2024·山东滨州·中考）如图6，在中，点，分别在边 ，
上.添加一个条件使 ，这个条件可以是_____________
_______________.（写出一种情况即可）
（答案不唯一）
图6
7.（2025·辽宁·中考改编）如图7，，与相交于点 ，且
与的周长比是，若，则 的长为____.
12
图7
提示：由，得.所以，即 .解得
.
图8
8.（2025·湖南邵阳·中考模拟）如图8， ，
，是线段上的一点，且 ，
，， .
（1）求证： .
证明： ，，， .
， .
.
（2）求线段 的长.
图8
解： ， ，即.解得 .
攻坚练
图9
9.如图9，在中，直尺的一边与 重合，
另一边分别交，于点，E.其中点 ，
，，处的读数分别为8，16，， .
已知直尺的宽为3，则中边 上的高为
( ).
A.2 B.3 C.4 D.6
图9
提示：过点A作于点，交于点 .
由题意，得 ，
.由 ，得
，.所以 ，即
【答案】D
.解得.故中边 上的高为6.
图10
10.（2025·四川内江·中考模拟）如图10，在 中，
，为边的三等分点，点，在边 上，
，为与的交点.若 ，则
的长为( ).
A.1 B. C.2 D.3
提示：由D，为边 的三等分点，得，，.由 ，得.所以，即 .解得
.由，得.所以 ，即.解得 .
C
图11
11.跨学科题（2024·江苏扬州·中考）同学们在物理课
上学过小孔成像的原理，它是一种利用光的直线传播
特性实现图像投影的方法.如图11，燃烧的蜡烛
（竖直放置）经小孔 在屏幕（竖直放置）上成像
.设，，小孔到 的距
离为，则小孔到的距离为____ .
20
提示：设小孔到的距离为.由题意，得 ，则
.解得，即小孔到的距离为 .
图12
12.（2024·四川眉山·中考）如图12，菱形 的边
长为6， ，过点作，交 的
延长线于点，连接分别交，于点， ，则
的长为_ ___.
图12
提示：由菱形的性质，得 ，， .从而得 .在 中，， .由此可得.由，得 ，在中，.由 ，得.从而得 .所以.由，得 .从而 得.所以 .故 .
图13
13.（2025·浙江杭州·模拟）如图13，在矩形 中，
是的中点，于点，连接交于点 ，
连接 .
（1）当时，求 的值.
解： 是的中点，，
四边形是矩形， ， ，.
， .
∴
∴ .
（2）当时，求 的值.
图13
解：如图40，延长交的延长线于点 ，连接，
四边形是矩形，∴ ，， .
∴
.
∴
是的中点，
图40
四边形 是平行四边形.
， 四边形是菱形.
∴ ，，
∴ .
∴ .
∴ .
，∴
∴ .
∴ .
图40
拔尖练
14.（2024·四川自贡·中考）为测量水平操场上旗杆的高度，九年级2班
各学习小组运用了多种测量方法.
图14
（1）如图14，小明在测量时发现，自己在操场上的影长
恰好等于自己的身高.此时，小组同学测得旗杆
的影长为，据此可得旗杆高度为_____ .
11.3
提示：由题意，得.从而得 .又
，所以 .
图15
（2）如图15，小李站在操场上点 处，前面水
平放置镜面，并通过镜面观测到旗杆顶部 .小
组同学测得小李的眼睛距地面高度 ，
小李到镜面距离 ，镜面到旗杆的距离
.求旗杆高度 .
解：由题意可知，又 ，
，即.
解得 .
答：旗杆高度为 .
（3）小英所在小组采用图16的方法测量旗杆高度，结果误差较大.
图16
在更新测量工具，优化测量方法后，测量精度明显提高，研学旅行时，他们利用自制工具，成功测量了某广场雕塑的高度.方法如下：如图
17，在透明的塑料软管内注入适量的水，利用连通器原理，保持管内水面，两点始终处于同一水平线上.如图18，在支架上端点 处，用细线系小重物，标高线 始终垂直于水平地面.
图17
图18
如图19，在广场上点处，同学们用注水管确定与雕塑底部 处于
同一水平线的，两点，并标记观测视线与标高线的交点 ，测得
标高，.将观测点后移到点 处.采用同样
方法，测得，.求雕塑高度.（结果精确到 ）
图19
解： ， ，
.
设，，则.∴ .
同理可得
，即.
∴ .
解得.经检验， 是原方程的解，且符合题意.
故.
答：雕塑高度约为 .