2026年中考《数学》复习课件 专题六 圆-第25讲 圆的有关概念和性质(共55张PPT)

(共55张PPT)
复习讲义
第一篇 考点精讲
专题六 圆
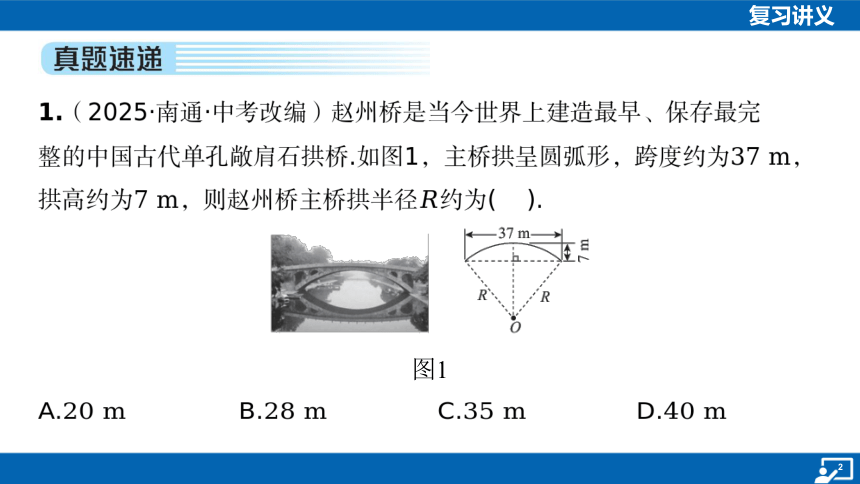
1.（2025·南通·中考改编）赵州桥是当今世界上建造最早、保存最完
整的中国古代单孔敞肩石拱桥.如图1，主桥拱呈圆弧形，跨度约为 ，
拱高约为，则赵州桥主桥拱半径 约为( ).
图1
A. B. C. D.
图35
提示：如图35，由题意知，， .
设主桥拱半径 ，所以
．因为是 半径，
，所以 ．在
中， ，所以
【答案】B
.解得．所以赵州桥主桥拱半径 约为
.
图2
2.（2024·广西·中考第24题）如图2，已知是
的外接圆，，分别是， 的中点，连
接并延长至点，使，连接 .
（1）求证：四边形 是平行四边形.
证明： ，分别是，的中点， 是 的中位线.
∴ ，且.
又，∴
∴ 四边形 是平行四边形.
（2）求证：与 相切.
图2
证明：如图36，连接
,, ,是 的垂直平分线.
又 是的外心， 点在 上.
由（1）可知，， .
又 是的半径， 与 相切.
图36
图2
（3）已知，，求 的半径.
解：如图36，连接.
由（2）可知， ，
， .
又∵ ,∴
.
在中，
的半径 .
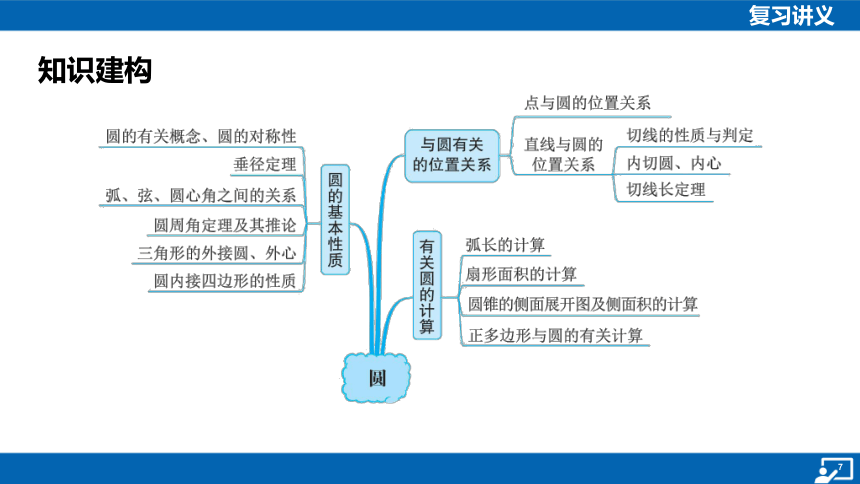
知识建构
第25讲 圆的有关概念和性质
聚焦核心
1.圆的基础知识
圆 平面上到定点的距离等于定长的所有点组成的图形叫作圆，定
点称为______，定长称为______
弧 圆上任意______间的部分叫作弧
弦、 直径 连接圆上任意两点的______叫作弦，经过______的弦叫作直径
对称 性 圆是轴对称图形，任何一条______所在的直线都是圆的对称轴
圆是中心对称图形，对称中心是______
圆心
半径
两点
线段
圆心
直径
圆心
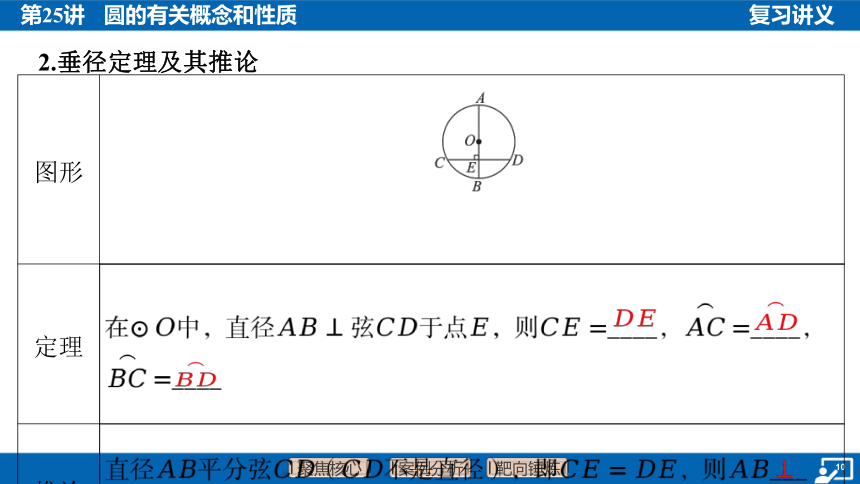
2.垂径定理及其推论
图形 ________________________________________
定理 在中，直径 弦于点，则____， ____，
____
推论 直径平分弦（不是直径），即，则 ___
，____， ____
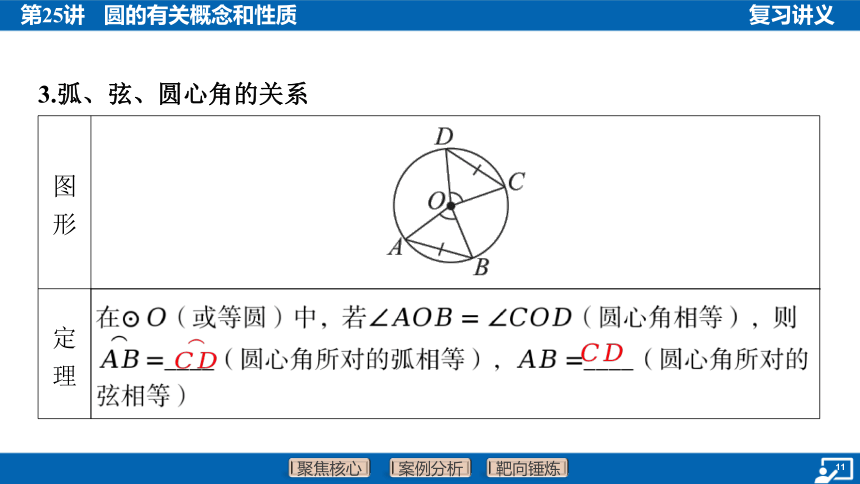
3.弧、弦、圆心角的关系
图 形 ______________________________________
定 理 在（或等圆）中，若 （圆心角相等），则
____（圆心角所对的弧相等）， ____（圆心角所对的
弦相等）
推 论 在（或等圆）中，若（两条弧相等），则 _______（弧所对的圆心角相等）， ____（弧所对的弦相等）
在（或等圆）中，若（两条弦相等），则_______（弦所对的圆心角相等）， ____（弦所对的弧相等）
续表
4.圆周角定理及其推论
定义 顶点在____上，并且两边都与圆______的角叫作圆周角
定理 一条弧所对的圆周角等于它所对的________的一半
推论 在同圆或等圆中，同弧或等弧所对的圆周角______；相等的
圆周角所对的弧也______
半圆（或直径）所对的圆周角是____角， 的圆周角所对
的弦是______
圆
相交
圆心角
相等
相等
直
直径
5.圆内接多边形
（1）如果一个多边形的所有顶点都在________圆上，那么这个多边形
叫作这个圆的内接多边形，这个圆叫作多边形的外接圆.
（2）圆内接四边形的对角______.
同一个
互补
第25讲 圆的有关概念和性质
案例分析
考点一 垂径定理及其推论
名师指导
图1
垂直于弦的直径平分这条弦，因此利用垂径定理求线段的长时，可连半径或过圆心作垂直于弦的垂线段，构造由半径、半弦和过圆心且垂直于弦的垂线段组成的直角三角形，如图1，从而得到：
， .
图2
例1 （2024·四川凉山·中考）数学活动课上，同学们要
测一个如图2所示的残缺圆形工件的半径.小明的解决方
案是：在工件圆弧上任取两点，，连接，作 的
垂直平分线交于点，交于点 ，测出
A. B. C. D.
， ，则圆形工件的半径为 ( ).
思路点拨 如图2，设圆心为点，连接，在 中，可用半径
表示出 的长，进而可根据勾股定理列方程求出圆形工件的半径.
图2
提示：因为是线段的垂直平分线，所以直线
经过圆心.设圆心为点，连接.在 中，
.根据勾股定理，得
，即 .解得
.故这个圆形工件的半径为 .
【答案】C
考点专练
图3
1.（2024·湖南长沙·中考改编）如图3，在半径为 的
中，弦的长为8，则圆心到的距离 为( ).
B
A. B.4 C.2 D.
2.跨学科题（2025·广西梧州·模拟）图4是化学实验中常使用的一种球形
蒸馏瓶，它的底部可以看成是一个球体，这个球体最大纵截面如图5所
示，其半径为，瓶内液体最大深度为，则液面宽 为( ).
图4
图5
A. B. C. D.
提示：如图37，连接，过点作于点D，则 .根据题意，得， .所以.故 .
D
图37
考点二 弧、弦、圆心角之间的关系
名师指导
在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相
等，那么它们所对应的其余各组量都分别相等.根据这一定理，可以进
行圆中弧、线段、角之间的相互转化，为计算角的度数、线段的长或证
明线段相等、角相等，证明三角形全等、特殊四边形等提供条件.
图6
例2 教材变式［沪科版九下第19页例4变式］如图6，在
中，， .
（1）求 的度数.
思路点拨
（1）
解： ， ．又 ， ， .
的度数是 ．
图6
（2）求证： 是等边三角形.
图6
证明： ，
是等边三角形．
（2）
思路点拨
考点专练
图7
3.（2025·湖南衡阳·模拟）如图7，是 的直径，
四边形内接于.若 ，则
的直径 为( ).
D
A. B. C. D.
图8
4.如图8，已知，，，是上的点， ，给
出下列结论：，， ，
.其中正确的结论是__________.
（填序号）
①②③④
考点三 圆周角定理及其推论
名师指导
1.在解决与圆周角有关的问题时，常利用同弧所对的圆周角和圆心
角的关系，进行角之间的转化和计算.
2.由于直径所对的圆周角是直角，因此条件中出现直径时，常寻找
或构造直径所对的圆周角，然后利用解直角三角形的知识解决问题.
图9
例3 （2024·山东泰安·中考）如图9，是 的直
径，，是上两点，平分 .若
，则 的度数为( ).
A. B. C. D.
思路点拨
提示：由平分，得.因为是 的直径，
，所以 ， .从而得
.故 .
答案：A
图9
考点专练
图10
5.（2024·甘肃临夏·中考）如图10，是 的直径，
，则 的度数是( ).
D
A. B. C. D.
图11
6.（2024·四川宜宾·中考）如图11，是 的直径，
若 ，则 的度数是( ).
A
A. B. C. D.
提示：由是的直径，得 .又
.所以 .
考点四 圆内接四边形的性质
图12
名师指导
在解答涉及圆的内接四边形的证明或计算的问
题时，可以运用“圆内接四边形的对角互补”求角或
进行角的转换.特别地，对于选择、填空题，我们可
以直接运用“圆内接四边形的任何一外角等于它的内
对角”进行计算，如图12，四边形为的内接四边形，则
.
图13
例4 （2024·四川广元·中考）如图13，已知四边形
是的内接四边形，为 延长线上一点，
，则 的度数为( ).
A. B. C. D.
思路点拨
提示：因为与分别是 所对的圆周角和圆心角，所以 .因为四边形是 的内接四边形，所以 .又 ，所以 . （或利用“圆内接四边形的任何一外角等于它的内对角” 直接得到 ）
答案：A
图13
考点专练
7.（2024·青海·中考）如图14，四边形是 的内接四边形.若
，则 的度数是______.
图14
图15
8.（2024·山东滨州·中考）如图15，四边形 内接于
，若四边形是菱形，则 的度数是____.
提示：因为四边形内接于 ，所以
.因为四边形 是菱形，所以
.由圆周角定理，得 .所以
.解得 .
第25讲 圆的有关概念和性质
靶向锤炼
靶向练
图1
1.（2025·大庆·中考模拟）如图1，点，，在 上，
，则 的度数是( ).
D
A. B. C. D.
图2
2.（2024·云南·中考）如图2，是的直径，点， 在
上.若， ，则 的度数为( ).
B
A. B. C. D.
提示：连接，由 ，得
.
图3
3.如图3，在中，是直径， ，则下列结
论不一定成立的是( ).
C
A.
B.
C.
D.点到, 的距离相等
图4
4.数学文化（2025·湖南岳阳·中考模拟）我国古代数学名著
《九章算术》中有一道关于圆的数学题，其大意是：如
图4，今有圆形材质，直径 为25，要做成方形板材，
使其厚度达到7，则 的长是( ).
C
A. B.25 C.24 D.7
图5
5.（2024·新疆·中考）如图5，是的直径，是
的弦，，垂足为点.若，，则
的长为( ).
B
A.1 B.2 C.3 D.4
提示：因为是的直径，且 ，所以
.在中，，故 .
图6
6.（2024·吉林·中考）如图6，四边形内接于 ，
过点作，交于点.若 ，则
的度数是( ).
C
A. B. C. D.
图7
7.（2024·内蒙古通辽·中考）如图7，圆形拱门最下端 在
地面上，为的中点，为拱门最高点，线段 经过拱
门所在圆的圆心.若， ，则拱门所在
圆的半径为( ).
B
A. B. C. D.
提示：由题意，得，.连接 ，设拱门所在圆
的半径为，则.而，所以 .
由勾股定理，得.解得 .故拱门所在圆的半径
为 .
图8
8.（2024·黑龙江牡丹江·中考）如图8，四边形 是
的内接四边形，是 的直径，若
，则 的度数为( ).
B
A. B. C. D.
提示：连接.由是的直径，得 .因
为 ，所以 .所以
.因为四边形是
的内接四边形，所以 .
9.（2024·北京·中考）如图9，的直径平分弦 （不是直径）.若
，则 的度数是____.
图9
图10
10.（2024·陕西·中考）如图10，是 的弦，连接
，，是所对的圆周角，则____ .
90
提示：过点作于点.因为 ，所以
.又，所以 .又
，所以 .
攻坚练
图11
11.（2025·内蒙古包头·中考模拟）如图11， 是锐角三角形
的外接圆，，， ，垂足分
别为点，，，连接，，.若 ，
的周长为21，则 的长为( ).
A.8 B.4 C.3.5 D.3
图11
提示：因为，， ，所以，，.所以，， 是的中位线.所以， ， .所以 .又因为，所以 ．
【答案】B
12.如图12，是半圆的三等分点，是的中点，是直径 上一动点.若的半径为1，则 的最小值为____.
图12
提示：如图50，作点关于的对称点 ，根据圆的对称性，可知点在上.连接交于点 ，则此时， 的值最小，最小值为的长.连接，， ，因为，所以 .因为是 的中点，所以 .由此可得， .在R中，，即的最小值为 .
图50
图13
13.一题多问 如图13，是的直径，点，在
上，连接，，，，于点 .
（1）当，时，求直径 的长.
解： ，， .
在 中，，
.
连接，则 .
在中，，即
.
（2）当，时，求直径 的长.
图13
解： 是的直径， .
， 垂直平分
.
在中， .
（3）将题目中“是的直径”改为“是的弦”，且 ，，求 的直径.
图13
图51
解：如图51，连接并延长交于点 ，连接
为的直径， ，即 .
，∴ .
，∴
.
.
.
在中，，即的直径为 .
拔尖练
图14
14.（2024·浙江·中考）如图14，在圆内接四边形中，， ，延长至点，使，延长至点 ，连接，使 .
（1）当 ，为直径时，求 的度数.
解： 为直径， .
， .
.
（2）求证：； .
图14
证明： 四边形 是圆内接四边形， .
又， . .
②如图52，过点作 交于点，连接，
，
四边形是圆内接四边形， .
又 ，
，，
图52
图52
， ， .
在和 中，，， ，
.