第十三章 三角形章末复习练习 2025-2026学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 第十三章 三角形章末复习练习 2025-2026学年人教版八年级数学上册(含答案) | 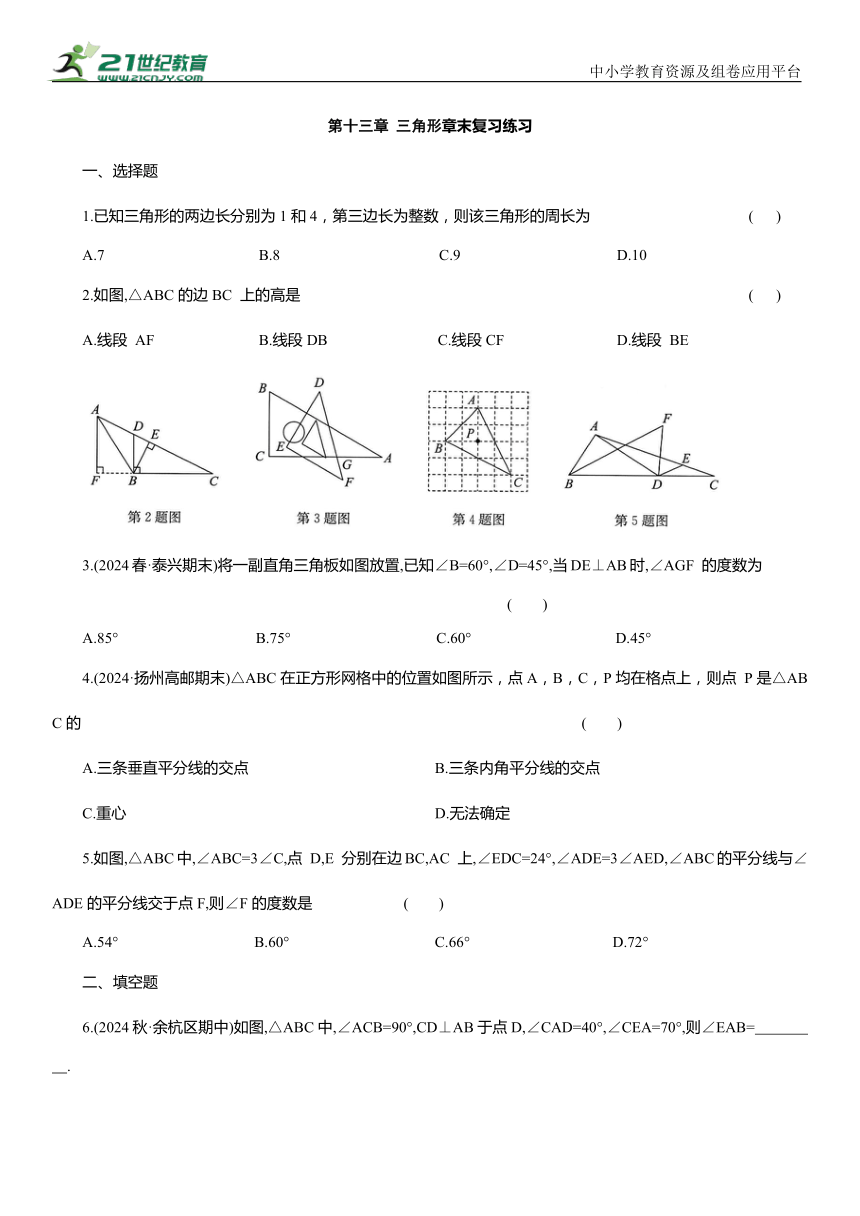 | |
| 格式 | docx | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 23:33:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十三章 三角形章末复习练习
一、选择题
1.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为 ( )
A.7 B.8 C.9 D.10
2.如图,△ABC的边BC 上的高是 ( )
A.线段 AF B.线段DB C.线段CF D.线段 BE
3.(2024春·泰兴期末)将一副直角三角板如图放置,已知∠B=60°,∠D=45°,当DE⊥AB时,∠AGF 的度数为 ( )
A.85° B.75° C.60° D.45°
4.(2024·扬州高邮期末)△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点 P是△ABC的 ( )
A.三条垂直平分线的交点 B.三条内角平分线的交点
C.重心 D.无法确定
5.如图,△ABC中,∠ABC=3∠C,点 D,E 分别在边BC,AC 上,∠EDC=24°,∠ADE=3∠AED,∠ABC的平分线与∠ADE的平分线交于点F,则∠F的度数是 ( )
A.54° B.60° C.66° D.72°
二、填空题
6.(2024秋·余杭区期中)如图,△ABC中,∠ACB=90°,CD⊥AB于点D,∠CAD=40°,∠CEA=70°,则∠EAB= .
7.小明把一副直角三角板按如图方式摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β= °.
8.如图,将△ABC纸片沿DE 折叠,使点A落在点A′处,且BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=112°,则∠BA′C 的度数为 .
三、解答题
9.如图, 中,AD⊥BC于点D,BE是 的平分线,若
(1)求∠EBC的度数;
(2)求∠AOB的度数.
10.(2024春·泰兴期末)如图, 的顶点在正方形网格的格点上,请按要求画图并回答问题:
(1)请画图,找出△ABC的重心点 P;
(2)请在△ABC的边上找一点D,使它与点A,B,C中的任意两点组成的三角形的面积是△ABC面积的
11.如图,CE平分∠ACD,F为CA 的延长线上一点,FG∥CE交AB 于点G,∠ACD=100°,∠AGF=20°,求∠B 的度数.
12.如图,已知锐角∠EAF,点B,C分别在射线AE,AF上.
(1)如图①,若∠EAF=56°,连接BC,∠ABC=α,∠ACB=β,∠CBE 的平分线与∠BCF的平分线交于点P,则α+β= °,∠P= °;
(2)若点Q在∠EAF 的内部(点Q不在线段 BC上),连接BQ,QC,∠EAF=56°,∠CQB=104°,BM,CN分别平分∠QBE和∠QCF,且BM与CN交于点D,求∠BDC的度数;
(3)如图②,G是线段CB的延长线上一点,过点G作GH⊥AE于点H,∠EAF与∠CGH的平分线交于点O,请直接写出∠ACG 与∠AOG 的数量关系,并说明理由.
1. C 2. A 3. B 4. C 5. B 6.20° 7.285 8.118°
9.解:(1)∵AD⊥BC,∴∠ADC=90°,
∴△ADC是直角三角形.
∵∠DAC=30°,∴∠C=90°-∠DAC=60°.
∵∠BAC=80°,∴∠ABC=180°-∠BAC-∠C=40°.
∵BE 是∠ABC的平分线,∴
(2)∵∠BAC=80°,∠DAC=30°,
∴∠BAD=∠BAC-∠DAC=50°.
由(1)可知∠EBC=20°,
∵BE是∠ABC的平分线,∴∠ABO=∠EBC=20°,在△AOB中,∠AOB=180°-∠BAO-∠ABO=110°.
10.解:(1)如答图①,点 P 即为所求.
(2)如答图②,找到AB,BC的中点F,E,连接AE,CF交于点P,连接BP,延长BP交AC于点D.
依题意,在△ABC的边上找一点D,使它与点A,B,C中的任意两点组成的三角形的面积是△ABC 面积的 则点 D,E,F 均满足题意.
11.解:∵CE平分∠ACD,
∵FG∥CE,∴∠AFG=∠ACE=50°.
在△AFG中,∠BAC=∠AFG+∠AGF=50°+20°=70°,又
∴∠B=180°-∠BAC-∠ACB=180°-70°-80°=30°.
12.(1)124 62
(2)解:①当点 Q在BC 的右侧时,如答图①.
∵∠ACQ+∠ABQ=360°-(∠EAF+∠CQB)=360°-(56°+104°)=200°,
∴∠FCQ+∠QBE=360°-(∠ACQ+∠ABQ)=160°.
∵BM,CN分别平分∠QBE,∠QCF,
∵∠QCB+∠CBQ=180°-∠CQB=76°,
∴∠DCB+∠DBC=80°+76°=156°,
∴∠BDC=180°-(∠DCB+∠DBC)=180°-156°=24°.
②当点 Q在BC 的左侧时,如答图②.
∵∠ACB+∠ABC=180°-∠EAF=124°,
∴∠ACQ+∠ABQ=124°-76°=48°,
∴∠FCQ+∠QBE=360°-48°=312°,
∴∠BDC=360°—156°—104°=100°.
综上所述,∠BDC的度数为24°或 100°.
(3)解: 理由如下:如答图③.
∵AO,GO分别是∠FAE 和∠CGH 的平分线,
∵∠1=∠CAO+∠ACG=∠CGO+∠AOG,
即
∵∠ABC=∠GBH,
∴∠EAF=180°-∠ACG-∠ABC=180°-∠ACG-∠GBH,∠CGH=90°-∠GBH,
第十三章 三角形章末复习练习
一、选择题
1.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为 ( )
A.7 B.8 C.9 D.10
2.如图,△ABC的边BC 上的高是 ( )
A.线段 AF B.线段DB C.线段CF D.线段 BE
3.(2024春·泰兴期末)将一副直角三角板如图放置,已知∠B=60°,∠D=45°,当DE⊥AB时,∠AGF 的度数为 ( )
A.85° B.75° C.60° D.45°
4.(2024·扬州高邮期末)△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点 P是△ABC的 ( )
A.三条垂直平分线的交点 B.三条内角平分线的交点
C.重心 D.无法确定
5.如图,△ABC中,∠ABC=3∠C,点 D,E 分别在边BC,AC 上,∠EDC=24°,∠ADE=3∠AED,∠ABC的平分线与∠ADE的平分线交于点F,则∠F的度数是 ( )
A.54° B.60° C.66° D.72°
二、填空题
6.(2024秋·余杭区期中)如图,△ABC中,∠ACB=90°,CD⊥AB于点D,∠CAD=40°,∠CEA=70°,则∠EAB= .
7.小明把一副直角三角板按如图方式摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β= °.
8.如图,将△ABC纸片沿DE 折叠,使点A落在点A′处,且BA′平分∠ABC,CA′平分∠ACB,若∠1+∠2=112°,则∠BA′C 的度数为 .
三、解答题
9.如图, 中,AD⊥BC于点D,BE是 的平分线,若
(1)求∠EBC的度数;
(2)求∠AOB的度数.
10.(2024春·泰兴期末)如图, 的顶点在正方形网格的格点上,请按要求画图并回答问题:
(1)请画图,找出△ABC的重心点 P;
(2)请在△ABC的边上找一点D,使它与点A,B,C中的任意两点组成的三角形的面积是△ABC面积的
11.如图,CE平分∠ACD,F为CA 的延长线上一点,FG∥CE交AB 于点G,∠ACD=100°,∠AGF=20°,求∠B 的度数.
12.如图,已知锐角∠EAF,点B,C分别在射线AE,AF上.
(1)如图①,若∠EAF=56°,连接BC,∠ABC=α,∠ACB=β,∠CBE 的平分线与∠BCF的平分线交于点P,则α+β= °,∠P= °;
(2)若点Q在∠EAF 的内部(点Q不在线段 BC上),连接BQ,QC,∠EAF=56°,∠CQB=104°,BM,CN分别平分∠QBE和∠QCF,且BM与CN交于点D,求∠BDC的度数;
(3)如图②,G是线段CB的延长线上一点,过点G作GH⊥AE于点H,∠EAF与∠CGH的平分线交于点O,请直接写出∠ACG 与∠AOG 的数量关系,并说明理由.
1. C 2. A 3. B 4. C 5. B 6.20° 7.285 8.118°
9.解:(1)∵AD⊥BC,∴∠ADC=90°,
∴△ADC是直角三角形.
∵∠DAC=30°,∴∠C=90°-∠DAC=60°.
∵∠BAC=80°,∴∠ABC=180°-∠BAC-∠C=40°.
∵BE 是∠ABC的平分线,∴
(2)∵∠BAC=80°,∠DAC=30°,
∴∠BAD=∠BAC-∠DAC=50°.
由(1)可知∠EBC=20°,
∵BE是∠ABC的平分线,∴∠ABO=∠EBC=20°,在△AOB中,∠AOB=180°-∠BAO-∠ABO=110°.
10.解:(1)如答图①,点 P 即为所求.
(2)如答图②,找到AB,BC的中点F,E,连接AE,CF交于点P,连接BP,延长BP交AC于点D.
依题意,在△ABC的边上找一点D,使它与点A,B,C中的任意两点组成的三角形的面积是△ABC 面积的 则点 D,E,F 均满足题意.
11.解:∵CE平分∠ACD,
∵FG∥CE,∴∠AFG=∠ACE=50°.
在△AFG中,∠BAC=∠AFG+∠AGF=50°+20°=70°,又
∴∠B=180°-∠BAC-∠ACB=180°-70°-80°=30°.
12.(1)124 62
(2)解:①当点 Q在BC 的右侧时,如答图①.
∵∠ACQ+∠ABQ=360°-(∠EAF+∠CQB)=360°-(56°+104°)=200°,
∴∠FCQ+∠QBE=360°-(∠ACQ+∠ABQ)=160°.
∵BM,CN分别平分∠QBE,∠QCF,
∵∠QCB+∠CBQ=180°-∠CQB=76°,
∴∠DCB+∠DBC=80°+76°=156°,
∴∠BDC=180°-(∠DCB+∠DBC)=180°-156°=24°.
②当点 Q在BC 的左侧时,如答图②.
∵∠ACB+∠ABC=180°-∠EAF=124°,
∴∠ACQ+∠ABQ=124°-76°=48°,
∴∠FCQ+∠QBE=360°-48°=312°,
∴∠BDC=360°—156°—104°=100°.
综上所述,∠BDC的度数为24°或 100°.
(3)解: 理由如下:如答图③.
∵AO,GO分别是∠FAE 和∠CGH 的平分线,
∵∠1=∠CAO+∠ACG=∠CGO+∠AOG,
即
∵∠ABC=∠GBH,
∴∠EAF=180°-∠ACG-∠ABC=180°-∠ACG-∠GBH,∠CGH=90°-∠GBH,
同课章节目录
